统计学原理计算分析题教学题目答案
- 格式:doc
- 大小:1.54 MB
- 文档页数:29



第一章练习题参考答案一.单项选择题1.B;2.A;3.B;4.C;5.D;6.A;7.C;8.C;9.C;10.A;11.C;12.C。
二.多项选择题1.ABDE;2.ACD;3.BCD;4.ACD;5.ACDE;6.ACE;7.AD;8.ABC;9.ACD;10.AD;11.BCDE;12.ABCDE;13.AC。
三.判断题1.×;2.×;3.×;4.×;5.√;6.×;7.×;8.√;9.×;10.√。
第二章练习题参考答案一.单项选择题1.C;2.C;3.D;4.B;5.D;6.D;7.B;8.D;9.B;10.B;11.A;12.C;13.D。
二.多项选择题1.CE;2.ACE;3.CE;4.BCD;5.ABCE;6.BC;7.BCD;8.ABD;9.ABD;10.ACDE;11.ABCE;12.ABE。
三.判断题1.×;2.√;3.×;4.×;5.×;6.×;7.√;8.×;9.×;10.×。
第三章练习题参考答案一.单项选择题1.B;2.C;3.C;4.C;5.D;6.B;7.B;8.B;9.D;10.B;11.A;12.B;13.D;14.A。
二.多项选择题1.AB;2.AC;3.AB;4.ABC;5.AB;6.ABD;7.ABC;8.ACE;9.BD;10.ABDE。
三.判断题1.√;2.×;3.×;4.×;5.√;6.×;7.√;8.√;9.×;10.×。
四.计算分析题1.解:(1)按职称编制的分配数列2.解:编制单项式变量数列3.解:(1)编制组距式变量数列。
(2直方图(略)第四章练习题参考答案一.单项选择题1.C;2.D;3.B;4.D;5.C;6.A;7.C;8.C;9.B;10.C;11.B;12.D;13.A;14.D;15.16.B;17.B;18.D;19.C;20.C;21.D;22.B;23.C;24.C;25.B。

附录:参考答案第一章一、填空题1、统计调查;统计整理;统计分析2、统计工作;统计资料;统计科学3、调查;数量性;总体性;具体性;社会性4、总体单位(个体);总体5、性质相同;总体6、信息职能;咨询职能;监督职能;提供信息7、数量;品质二、单项选择题1、A2、C3、C4、B5、A6、B7、A8、B9、C 10、A三、简答题1、所谓统计,是人们认识客观世界总体现象数量特征、数量关系和数量变动规律的一种调查研究方法。
这种方法是对总体现象数量方面进行收集、整理和分析研究的总称,是人们认识客观世界的一种最有效的工具。
统计通常有三种涵义,即统计工作、统计资料和统计学,其中统计资料是统计工作的成果,统计学是统计工作的经验总结与理论概括。
2、统计是研究大量社会经济现象的数量方面的,如果总体各单位的标志和指标没有差异(变异),其具体表现都一样,那么只要调查一个便可知全体,这样就用不着统计了。
只有变异才能统计,变异是统计的前提。
3、标志是说明总体单位具有的特征,指标是说明总体的综合数量特征的。
区别:⑴标志是说明总体单位(个体)特征的;而指标是说明总体特征的。
⑵标志中的数量标志是可以用数值表示,品质标志不能用数值表示;而所有的指标都是用数值表示的,不存在不能用数值表示的指标。
⑶标志中的数量标志不一定经过汇总,可以直接取得;而指标是由数量标志汇总得来的。
⑷标志一般不具备时间、地点等条件;而作为一个完整的统计指标,一定要有时间、地点、范围。
联系:⑴一般来说,指标的数值是由标志值汇总而来的;⑵标志和指标存在着一定的变换关系。
4、统计研究的基本方法有大量观察法、统计分组法、综合指标法、统计模型法。
第二章一、项选择题1.B2.B3.D4.A5.B6.C7.B8.C二、判断题1.(×)2.(×)3.(×)4.(×)5.(√)6.(√)7.(×)8.(×)三、简答题1.相同点:三种调查都是一时性的非全面调查,都是从总体中抽出一部分单位进行调查。

第一章总论一、单项选择题1.威廉·配第是(B )的代表人物。
A.记述学派B.政治算术学派C.社会学派D.数理统计学派2.以下属于推断统计学研究范围的是(D)。
A.数据调查与收集B.数据的计算C.数据汇总D.抽样估计3.调查某企业职工的健康状况,总体单位是(D )。
A.这个企业B.所有的职工C.每个职工D.每个职工的健康状况4.数量指标表现为(C)。
A.相对数В.平均数C.绝对数D.变异数5.名义级数据可以用来(A )。
A.分类B.比较大小C.加减运算D.加、减、乘、除四则运算6.间距级数据之间不可以(D )。
A.比较是否相等B.比较大小C.进行加减运算D.进行乘除运算7.2个大学生的身高分别为165厘米、172厘米,则165、172是(D )。
A.2个变量B. 2 个标志C.2个指标D. 2个数据8.总体与总体单位的确定(A)。
A.与研究目的有关B.与研究目的无关C.与总体范围大小有关D.与研究方法有关9,通过有限数量的种子发芽试验结果来估计整批种子的发芽率,这种统计方法属于(A)。
A. f断统计学B.描述统计学C.数学D.逻辑学10.国势学派对统计学的主要贡献是(C)A.采用了数量分析方法B.引入了大数法则C.提出了“统计学"一词D.证明了小样本理论11.统计学是一门关于研究客观事物数量方面和数量关系的(C )。
A.社会科学B.自然科学C.方法论科学D.实质性科学12.数理统计学的奠基人是(C )。
A.威廉·配第B.阿亭瓦尔C.凯特勒D.恩格尔13.统计学研究的特点是(B)A.大量性、总体性、变异性B.数量性、总体性、变异性C.大量性、总体性、同质性D.数量性、总体性、同质性14.通过测量或计算取得其值的是(B)A.品质变量B.连续变量C.离散变量D.以上都不对15.统计学的创始人是(A)。
A.威廉·配第B.阿享瓦尔C.凯特勒D.恩格尔二、多项选择题1.“统计”一词有三层含义,即(BD)。
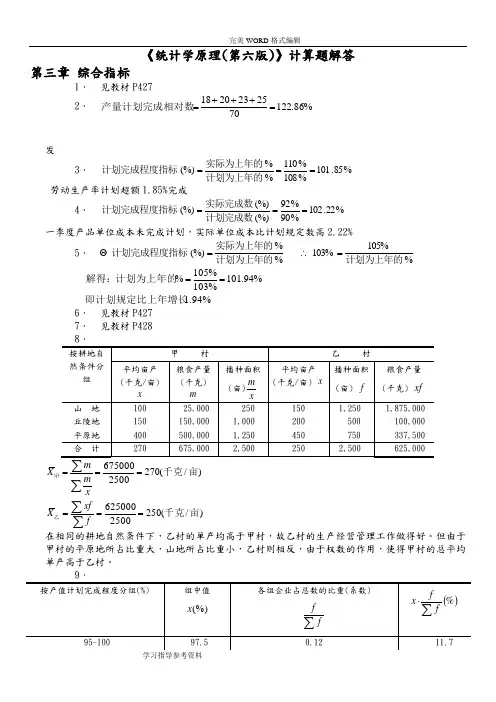
《统计学原理(第六版)》计算题解答第三章 综合指标1. 见教材P427 2. %86.1227025232018=+++=产量计划完成相对数发3. %85.101%108%110%%(%)===计划为上年的实际为上年的计划完成程度指标劳动生产率计划超额1.85%完成4. %22.102%90%92(%)(%)(%)===计划完成数实际完成数计划完成程度指标一季度产品单位成本未完成计划,实际单位成本比计划规定数高2.22%5. %105%103% %%(%) 计划为上年的计划为上年的实际为上年的计划完成程度指标=∴=1.94% %94.101103%105%% 即计划规定比上年增长计划为上年的解得:== 6. 见教材P427 7. 见教材P428 )/(2502500625000)/(2702500675000亩千克亩千克乙甲======∑∑∑∑f xf X xm m X在相同的耕地自然条件下,乙村的单产均高于甲村,故乙村的生产经营管理工作做得好。
但由于甲村的平原地所占比重大,山地所占比重小,乙村则相反,由于权数的作用,使得甲村的总平均单产高于乙村。
%.fx X 9103=⋅=∑∑平均计划完成程度10. 见教材P42811. %74.94963.09222.09574.03=⨯⨯=G X 12. (1)%49.51X %49.105 08.107.105.104.102.1 X 1624632121=-=⨯⨯⨯⨯=∑⋅⋅⋅⋅⋅⋅=G ff n f f G nX X X 平均年利率:平均本利率为:(2)%50.5 162%84%76%53%4%2X =⨯+⨯+⨯+⨯+==∑∑fXf)亩/283.3( 8.25275 251332562600275 组为30027530026002f d m f 1m S 2fX e M L 千克中位数所在=+=⨯-+=-∴==∑⋅--∑+=⎪⎪⎪⎭⎫⎝⎛)亩/(5.942 45.91275 25119)-(13384)-(133275d X M 84133211L 0千克=+=⨯++=⋅+=-∆+∆∆之间—在亩千克之间—在亩千克—众数所在组为325300Q )/(82.31282.12300 450460034f 3 2511938946003300250225Q )/(03.24203.17225 15046004f 25691034600225)300275(3311∴=+==⨯=⨯-⨯+=∴=+===⨯-+=∑∑Q Q (2)R=500-150=350(千克/亩))亩/41.84(60025102.14ff x x A.D.千克==∑∑-=(3))/(55.5225102.2250.1444-4.5642 252)600229(6002738.5d 2f )f d A -x (f f 2)d A -x (σ)/278(287.525600229A d f )f d Ax (x )亩/277.96(600166775f xf x 亩千克亩千克或千克=⨯=⨯=⨯--=⨯⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∑∑-∑∑==+⨯-=+⋅∑∑-===∑∑=“标准差”不要求用组距数列的简捷法计算 (4) 根据以上计算,294.5千克/亩>283.3千克/亩>277.96千克/亩,故资料分布为左偏(即下偏)。

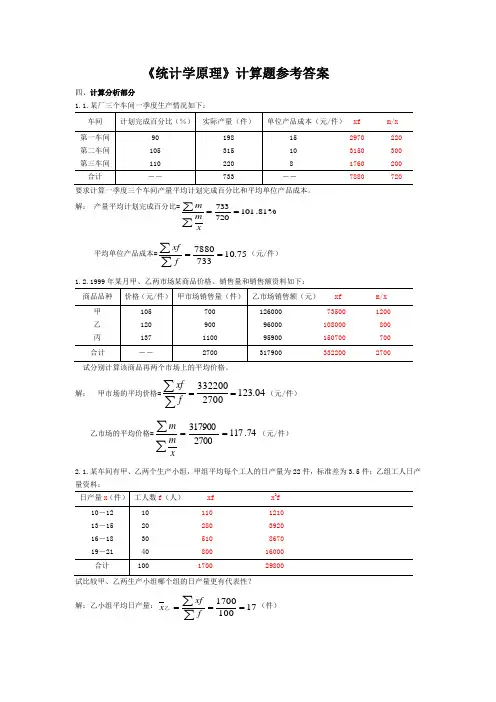
统计学原理课后计算题答案一、描述性统计1. 平均数计算给定一组数据:10, 15, 20, 25, 30平均数 = (10 + 15 + 20 + 25 + 30) / 5 = 202. 中位数计算给定一组数据:10, 15, 20, 25, 30中位数为中间的数值,即203. 众数计算给定一组数据:10, 15, 20, 20, 25, 30众数为浮现次数最多的数值,即204. 极差计算给定一组数据:10, 15, 20, 25, 30极差 = 最大值 - 最小值 = 30 - 10 = 205. 方差计算给定一组数据:10, 15, 20, 25, 30平均数 = (10 + 15 + 20 + 25 + 30) / 5 = 20方差 = [(10-20)^2 + (15-20)^2 + (20-20)^2 + (25-20)^2 + (30-20)^2] / 5 = 506. 标准差计算给定一组数据:10, 15, 20, 25, 30平均数 = (10 + 15 + 20 + 25 + 30) / 5 = 20方差 = [(10-20)^2 + (15-20)^2 + (20-20)^2 + (25-20)^2 + (30-20)^2] / 5 = 50标准差= √方差= √50 ≈ 7.07二、概率计算1. 单个事件概率计算一个骰子有6个面,每一个面的数字为1到6,每一个面浮现的概率相等,即1/6。
2. 互斥事件概率计算一个骰子有6个面,每一个面的数字为1到6,投掷骰子浮现奇数的概率为3/6 = 1/2。
投掷骰子浮现偶数的概率为3/6 = 1/2。
由于奇数和偶数是互斥事件,两者之一必然发生,所以概率之和为1。
3. 独立事件概率计算从一副扑克牌中抽取一张牌,不放回,再抽取一张牌。
第一次抽到红桃的概率为13/52 = 1/4。
第二次抽到红桃的概率为12/51 = 4/17。
由于两次抽取是独立事件,所以两者同时发生的概率为(1/4) * (4/17) = 1/17。
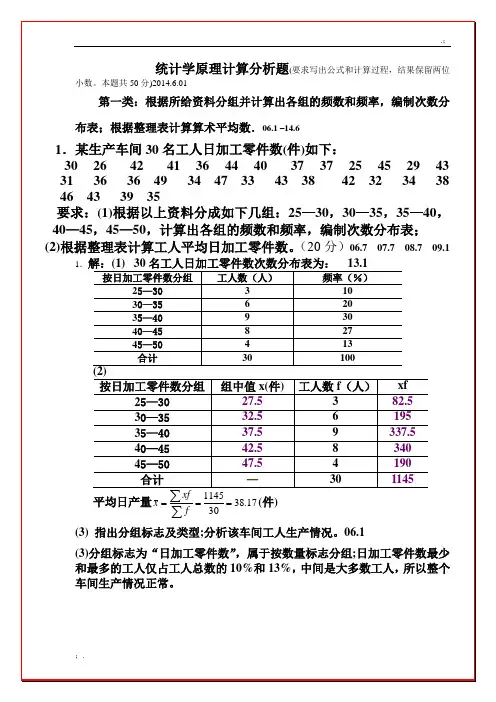
《统计学原理》计算题参考答案四、计算分析部分1.1.某厂三个车间一季度生产情况如下:要求计算一季度三个车间产量平均计划完成百分比和平均单位产品成本。
解: 产量平均计划完成百分比=%81.101720733==∑∑xm m平均单位产品成本=75.107337880==∑∑fxf (元/件) 1.2.1999年某月甲、乙两市场某商品价格、销售量和销售额资料如下: 试分别计算该商品再两个市场上的平均价格。
解: 甲市场的平均价格=04.1232700332200==∑∑fxf (元/件)乙市场的平均价格=74.1172700317900==∑∑xm m (元/件)2.1.某车间有甲、乙两个生产小组,甲组平均每个工人的日产量为22件,标准差为3.5件;乙组工人日产量资料:试比较甲、乙两生产小组哪个组的日产量更有代表性? 解:乙小组平均日产量:171001700===∑∑fxfx 乙(件)乙小组标准差:31710029800)()(22222=-=-=-=∑∑x ff x x x 乙σ(件)%91.15225.3===甲甲甲x V σ, %65.17173===乙乙乙x V σ, ∴乙甲〈V V 甲小组的日产量更有代表性2.2、有甲、乙两个品种的粮食作物,经播种实验后得知甲品种的平均产量为998斤,标准差为162.7斤;乙品种实验的资料如下:试研究两个品种的平均亩产量,以确定哪一个品种具有较大稳定性,更有推广价值? 解: 100155005===∑∑fxf 乙(斤) 45.72100155036250)()(22222=-=-=-=∑∑x ff x x x 乙σ(斤)%,3.169987.162===甲甲甲x V σ %2.7100145.72===乙乙乙x V σ ∴>乙甲V V 乙品种具有较大稳定性,更有推广价值3.1、某乡有10000户农户,按随机原则从中抽取100户,测得户均月收入3000元,标准差为400元,其中有20户的户均月收入在6000元以上。

第一章总论一、判断题1. √2. √3.×4. √5. ×6.×7.×8.×二、单选题1.C2.B3.D4.B5.C6.C7.C8.A9.B 10.C 11.A三、多选题1.ABCD(题目中的“五个”应去掉)2.ABE3.BDE4.BE5.AC6.AC第二章统计调查一、判断题1.×2.×3.×4.×5.√6.×7.×8.×9.× 10.√ 11.× 12.× 13.× 14.√ 15.√二、单选题1.B2.C3.C4.C5.C6.D7.D8.C9.D 10.D 11.D 12.C 13.A 14.C 15.A 16.B 17.A 18.B 19.A 20.D三、多选题1.ABCDE2.ABE3.BDE4.ABCD5.ABCDE第三章统计整理一、判断题1.×2.×3.×4.√5.√6.√7.×8.×9.× 10.× 11.√ 12.√二、单选题1.B2.B3.B4.A5.A6.C7.D8.C9.B 10.C 11.D 12.B 13.B三、多选题1.ADE2.CDE3.ABCD4.CD5.ACD6.ABCD7.CDE8.BC9.BCE四、计算题1.某班学生英语考试成绩频数分配表2.某生产车间工人日加工零件数频数分配表第4章综合指标一、判断题1. √2. ×3. ×4. √5. √6. ×7. ×8. ×9. × 10. ×11. × 12. √ 13. × 14. × 15. ×三、单选题1. B2. D3. C4. D5. C6. D7. C8. D9. B 10. A 11. D 12. B四、多项选择题1. ACE2. ABC3.BD4. BCD5. BCD6. ABD7. BCDE8. ACE 五、计算题 1.⑴ 企业2008年2007年实际销售额 2008年销售额为2007年的百分比(%) 计划 实际 完成计划(%)销售额比重(%) 销售额比重(%)甲 1200 30 1224 30.91 102 1100 111.27 乙 1000 25 1026 25.91 102.6 900 114 丙 1800 45 1710 43.18 95 1640 104.27 合计 40001003960100993640108.79⑵ 略2. ⑴ 计划完成程度=%108%10010028272726=⨯+++⑵ 设在第五年第二季度提前天X 完成,则:()100919127759123=-⨯++X X (天)5.45=X 即提前两个季度(6个月)又45天半完成5年计划。
试分别计算该商品在两个市场上的平均价格。
(20分)09.7 11.7 12.72014.1合计50—3870 —4312乙班学生的标准差()()分=乙29.924.865043122===-∑∑ffx x σ甲、乙两个生产小组, 甲组平均每个工人的日产量为36 件, 标准差为件; 乙组工人日产量资料如下:第三类:采用简单重复抽样的方法计算平均数(成数)的抽样平均误差;根据要3.某工厂有2000个工人,用简单重复方法抽出其100个工人作为样本出平均产量560件,标准差点32.45件.要求:(1)计算抽样平均平均误差;(2)以95.45%(z=2)的可靠性估计该厂工人的月平均产量及总产量区间.(20分)07.1解: (1)25.310045.32==nxσμ=(2)49.6245.32=⨯==∆μzx13.1(19. 某单位按简单随机重复抽样方式抽取40 名职工,对其业务情况进行考核,核成绩平均分数77分,标准差为1 0.54分.试以95. 45%的概率保证程度( Z= 2)断全体职工业务考试成绩的区间范围。
( 1 5分)11.7第四类:计算相关系数;建立直线回归方程并指出回归系数的含义;利用建立的方程预测因变量的估计值。
04.7 05.1 06.1 06.7 07.1 08.7 09.7 11.1 11.7 14.11.根据某地区历年人均收入(元)与商品销售额(万元)资料计算的有关数据如下:(x 代表人均收入,y 代表销售额):计算:(1)建立以商品销售额为因变量的直线回归方程,并解释回归系数的含义;(2)若2010年人均收为24000元,试推算该年的商品销售额。
06.7回归系数b 表示当人均收人每增加一元时,商品销售额平均增加0.92万元。
(2)预测2010年商品销售额 x=24000代入方程)(08.220532400092.092.2692.092.26万元=⨯+-=+-=x y c2.为研究产品销售额和销售利润之间的关系,某公司对所属地10家企业进行调查,设产品销售额为x(万元), 销售利润为y(万元).对调查资料进行进行整理和计算,其结果如下: n=10x ∑=795 y ∑=1065 2x∑=72925xy ∑=93200 ∑=1214752y要求:(1)计算销售额与销售利润之间的相关系数;(2)配合销售利润对销售额的直线线回归方程.(15分)07.1解: (1)计算相关系数;要求 :( 1)建立销售利润倚可比产品成本降低率的直线回归方程,预测可比(2 )计算学习时间和学习成绩之间的相关系数,并解释相关的密切程度和方向。
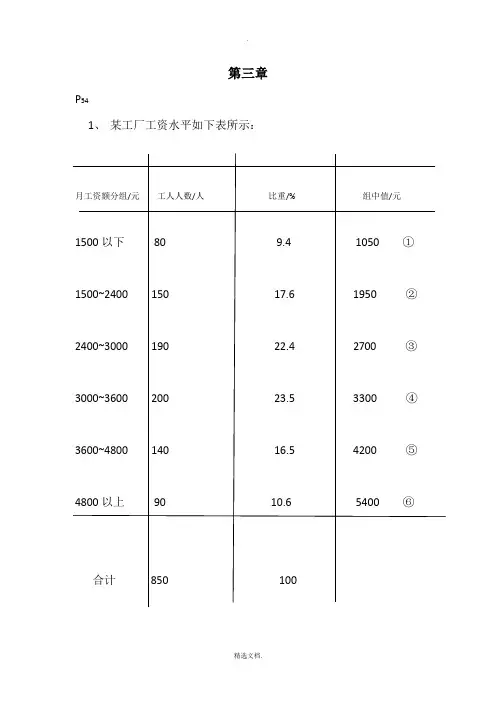
第三章P541、某工厂工资水平如下表所示:月工资额分组/元工人人数/人比重/% 组中值/元1500以下80 9.4 1050 ①1500~2400 150 17.6 1950 ②2400~3000 190 22.4 2700 ③3000~3600 200 23.5 3300 ④3600~4800 140 16.5 4200 ⑤4800以上90 10.6 5400 ⑥合计850 100=*100%工人人数比重总人数①2400-1500=-=1500-=105022相邻组组距缺下限的开口组组中值上限②~⑤ +=2上限下限组中值 ⑥4800-3600==4800+=540022相邻组组距缺上限的开口组组中值下限+第四章1.(1)该产品计划完成程度指标:252626.527.5100%105%100+++⨯=(2)0.590512 4.512622.52624⨯⨯-⨯+=+-() 答:该企业提前6个月22.5天完成五年计划规定指标。
2. 解: (1)480+598+600+612+120+180+250+1502500=119.6% (2) 提前完成计划时间=(计划期月数-计划完成月数)+超额完成计划数平均每日计划量数=(5*12-4.5*12)+9025005*365=8个月零6天答:该企业提前8个月6天完成五年计划规定指标。
3、(1)计算产量结构相对指标:2006年:甲车间=1200100%40%⨯=3000乙车间=1800100%60%⨯=30002007年:甲车间=2400100%60%⨯=4000乙车间=1600100%40%⨯=4000(2)2006年的平均单位成本=60040%70060%660⨯+⨯=2007年的平均单位成本=60060%70040%640⨯+⨯=2007年成本低的所占比重小,2008年成本低的所占比重大,甲成本较低,甲增产使总量增加,进而使成本降低。
4、平均工资=(500×60+600×100+700×140+800×60+900×40)400=680方差=(500-680)2×60+(600-680)2×100+(700-680)2×140+(800-680)2×60+(900-680)2×40400=136所以标准差=2136≈5、按平均每人约收入分组 /元职工户数f 组中值x 向上累计100-200 6 150 6200-300 10 250 16300-400 20 350 36 400-500 30 450 66 500-600 40 550 106 600-700 240 650 346 700-800 60 750 406 800-900 20 850 426 职工家庭平均每人月收入=1506250103502045030550406502407506085020619.486102030402406020xf f⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯==+++++++∑∑中位数位置=42621322f ==∑ 职工户数213在工资为[600,700]内中位数= 142610622600100644.58240m mfS L d f ---+⨯=+⨯=∑(元)职工户数最多集中在工资区间为[600,700]内 众数=24040600100652.63(24040)(24060)-+⨯=-+-分布特征:从平均数、中位数、众数可以知道,职工的月收入主要集中在600-700内,月收入少于600或大于700的人数较少,呈现出中间高,两边少的趋势。
6 . 6 5 . 6 2 . 6 0 . 6=6、86(百万元) 销售产值平均增长量==0、2(百万元) 销售产值平均进展速度==102、96% 销售产值平均增长速度=102、96%1=2、96% ③年平均职工人数: 1011171 112120222 120 118 114 116 110 106 108 98290b=111、7(人) 年平均工人数: 107371 1128086 82 80 75 74 72 70 66 60264a=73、7(人) 年平均工人数比重=65、98% ④年平均全员劳动生产率==0、0614(百万元)=6、14(万元)⑤年份 1994 1995 1996 1997 1998 1999 2000 2022 2022 2022 销售产值(百万元)y 6、0 6、2 6、5 6、6 6、9 7、0 6、9 7、2 7、5 7、8 68、6 t 1 2 3 4 5 6 7 8 9 10 551 4 9 16 25 36 49 64 81 100 385 ty 6 12、4 19、5 26、4 34、5 42 48、3 57、6 67、5 78 392、2 设销售产值得趋势直线方程为,根据最小平方法原理有:将计算表中数据代入有: 68、6=10a+55b 392、2=55a+385b b=0、1806 a=5、8667 代入方程得:y=5、8667+0、1806t 2022 年估计销售产值=5、8667+0、180612=8、0339(百万元) 2022 年估计销售产值=5、8667+0、180613=8、2145(百万元) 2022 年估计销售产值=5、8667+0、180614=8、3951(百万元) (4)①同季平均法季节比率计算表年份一季度二季度三季度四季度合计 2000 2022 2022 51 65 76 75 67 77 87 82 89 54 62 73 267 276 315 合计 192 219 258 189 858 季平均 64 73 89 73 71、5 季节比率(%) 89、51 102、1 120、28 88、11 100 剔出长期趋势季节变动分析表年份季别产值 y 4 项移动平均修正移动平均 t y/t100% 2000 1 2 3 4 51 57 87 54 66、75 70、25 68、5 69、25 127、0 78、0 2022 1 2 3 4 65 67 82 62 68、25 67 69 71、75 67、625 68 70、375 73 96、1 98、5 116、5 84、9 2022 1 2 3 4 76 77 89 73 74、25 76 78、75 75、125 77、375 101、2 99、5 剔出长期趋势后季节比率计算表1 季度%2 季度%3 季度%4 季度% 合计 2000 2022 2022 96、1 101、2 98、5 99、5 127、0 116、5 78、0 84、9 合计 197、3 198 243、5 162、9 季节指数(%) 98、7 99 121、75 81、5 400、95 调整后季节指数(%) 98、5 98、8 121、4 81、3 400 ②2022 年无季节变动下得销售(4)(5)(6)(7) 4、计算题: (1) 企业编号生产性固定资产总值 x 总产值 y 1 2 3 4 5 6 7 8 9 343 194 345 626 729 380 445 380 469 531 376 403 812 910 487 773 487 627 37636 670817294410 11 12 621 371 259 856 540 572 5162 7374① 8995 . 07374 4889706 12 5162 2494776 127374 5162 3454046 122 2二者成高度正相关。
统计学原理课后答案1. 问题一的答案根据统计学原理,问题一要求计算一个数据集的均值。
均值是指一组数据的平均数,可以通过将所有数据求和,然后除以数据的个数来得到。
下面是计算均值的公式:$$\\text{均值} = \\frac{\\text{数据之和}}{\\text{数据个数}}$$假设我们有一个数据集,其中包含10个数据点:5, 7, 3, 9, 2, 8, 6, 4, 1, 10。
使用上述公式,我们可以计算均值如下:$$\\text{均值} = \\frac{5 + 7 + 3 + 9 + 2 + 8 + 6 + 4 + 1 + 10}{10} =\\frac{55}{10} = 5.5$$因此,问题一的答案是5.5。
2. 问题二的答案问题二要求计算一个数据集的中位数。
中位数是指一组数据按照大小排序后中间的值,如果数据个数是奇数,则中位数是排序后位置处于中间的值;如果数据个数是偶数,则中位数是排序后中间两个值的平均值。
下面是计算中位数的步骤:1.对数据集进行排序;2.如果数据个数是奇数,则中位数是排序后位置处于中间的值;3.如果数据个数是偶数,则中位数是排序后中间两个值的平均值。
假设我们有一个数据集,其中包含10个数据点:5, 7, 3, 9, 2, 8, 6, 4, 1, 10。
按照上述步骤,我们可以计算中位数如下:1.对数据集进行排序:1, 2, 3, 4, 5, 6, 7, 8, 9, 10;2.数据个数是偶数,因此中位数是排序后位置处于中间的两个值:5 和6;3.中位数的平均值为(5+6)/2=5.5。
因此,问题二的答案是5.5。
3. 问题三的答案问题三要求计算一个数据集的众数。
众数是指一组数据中出现次数最多的值。
在某些情况下,一个数据集可能没有众数,也有可能有多个众数。
要计算众数,我们可以按照以下步骤进行:1.统计每个数据点出现的次数;2.找到出现次数最多的数据点。
假设我们有一个数据集,其中包含10个数据点:5, 7, 3, 9, 2, 8, 6, 4, 1, 10。
第一章总论二、单项选择题1.B 2.C 3.A 4.B 5.A6.D 7.D 8.B 9.D 10.D 11.C 12.A 13.C 14.D 15.D三、多项选择题1.ACE 2.ABD 3.BE 4.CE5.BDE 6.ABC 7.ACE 8.ABCE9.BCE 四、判断题1.×2.×3.√4.√5.×6.×7.√8.×第二章统计设计一、填空题(1)第一、各个方面、各个环节(2)整体设计、专项设计(3)全阶段设计、单阶段设计。
(4)长期设计、中期设计、短期设计。
(5)相互联系、相互制约(6)总体数量、概念、具体数值。
(7)总量指标、相对指标、平均指标(8) 数量指标、质量指标。
(9) 数量性、综合性、具体性。
(10) 国民经济统计指标体系、科技统计指标体系、社会统计指标体系二、多项选择题1.BE 2.AD 3.ABCE4.ACE 5.BD 6.ABC 7.CD 8.ABCD 9.ABCDE三、判断题1.√2.√3.×4.√5.√第三章统计调查一、填空题1.准确、及时、全面、系统。
2.基础资料。
3.全面、非全面、经常性、一次性、组织方式不同4.核心、原始资料5.国民经济(或国家)、地方、专业6.原始记录、统计台账7.一次性、全面8.全面、非全面9.原始、次级10.范围11.重点调查、典型调查12.普查、全面统计报表、重点调查、典型调查、抽样调查13.明确调查目的14.调查单位15.调查表、表头、表体、表脚、单一、一览16.开放式问题、封闭式问题二、单项选择题1.C 2.B 3.C 4.D 5.C 6.D 7.D 8.D 9.D 10.D 11.B 12.C 13.B 14.A 15.B 16.B 17.A 18.B三、多项选择题1.ADE 2.ACDE 3.AE4.ACE 5.ABC 6.CD 7.ACD 8.ABC 9.ABCDE 10.DE 11.BCDE第四章统计整理二、单项选择题1.C 2.A 3.B 4.B 5.B 6.C 7.C 8.C 9.A 10.C 11.C 12.A 13.B 14.C 15.B三、多项选择题1.AC 2.CE 3.DE 4.BCDE 5.ACD 6.ABE7.ABE 8.CD E9.ACD 10.ACDE四、判断题1.×2.×3.×4.√5.×6.√7.√8.√9.×10.√六、计算题1.分组标志为学习成绩,为数量标志,分组方法采用的是组距式分组。
3、统计调查的组织形式5、时期指标和时点指标的概念、区别 6、动态数列的定义、构成因素、模型10、抽样调查中存在哪些误差 11、抽样调查组织形式12、函数关系和相关关系的区别和联系 题型一:计算加权算术平均数、加权调和平均数、标准差、变异系数例题1:某车间有甲、乙两个生产组,甲组平均每个工人的日产量为36件,标准差为9.6件;乙组工人日产量资料如下:要求:⑴计算乙组平均每个工人的日产量和标准差;⑵比较甲、乙两生产小组哪个组的日产量更有代表性?解:5.291002950133438151345343538251515==+++⨯+⨯+⨯+⨯=∑∑fxf x =乙()986.810080752==-∑∑ff x x =乙σ267.0366.9==x V σ=甲3046.05.29986.8==x V σ=乙甲组更有代表性。
乙甲∴<V V例题2:乙两个生产小组,甲组平均每个工人的日产量为36件, 标准差为9.6件;乙组工人日产量资料如下:计算乙组平均每个工人的日产量,并比较甲、乙两生产小组哪个组的日产量更有代表性? 解答:7.281002870123139181245313539251815==+++⨯+⨯+⨯+⨯=∑∑f xf x =乙()127.910083312==-∑∑ffx x =乙σ267.0366.9==x V σ=甲 32.07.28127.9==x V σ=乙甲组更有代表性。
乙甲∴<V V题型2:动态数列相关指标的计算例题另知和平均流通费用率。
解:2006年下半年商品的平均流转次数:012/()/22n a nb b b b n=++++∑商品平均零售额商品平均流转次数=商品平均库存额(110711601150117012001370)6 1.77680710(675670650670690)622+++++÷==++++++÷(次)2006年下半年平均流通费用率为: 平均流通费用率=商品平均流通费用额商品平均零售额/(1081029895100104)66078.48%/(110711601150117012001n 370)67157a n yb n +++++÷====+++++÷∑∑例题3(1) 用最小二乘法拟合直线趋势方程(2)并预测该地区2007年该种产品的产量; 解:(1)用最小二乘法拟合直线趋势方程最小二乘法求参数的计算表设:ˆia bt y=+∑∑=tn ty n b 2=252.510=6.245123===∑nya ∴..ˆit y24625=+该企业这种产品产量2007年预测值为:ˆy2007=24.6+2.5×3=32.1(万吨)题型3、统计指数的编制(1)计算三种产品单位成本总指数及由于单位成本影响总成本的绝对额。
统计学原理试题及答案一、单项选择题(本大题共15小题,每小题1分,共15分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号D )。
A.对于所有的X,误差项的方差都相同B.误差项服从正态分布C.误差项相互独立2.某组数据分布的偏度系数为负时,该数据的众数、中位数、均值的大小关系是( A )。
A.众数>中位数>均值B.均值>中位数>众数C.中位数>众数>均值D.中位数>均值>众数3.一元回归方程为y=11.64一0.25x,则下列说法中正确的是( C )。
A.自变量平均增长一个单位,因变量减少0.25个单位B.自变量和因变量之间成正相关关系4.有甲乙两组数列,则(A )数列平均数的代表性高。
A.1<2 1>2,则乙数列平均数的代表性高B. 1<2 1>2,则乙数列平均数的代表性低C. 1=2 1>2,则甲数列平均数的代表性高D. 1=2 1<2,则甲数列平均数的代表性低5.某连续变量数列,其末组为开口组,下限为500,相邻组的组中值为480,则末组的组中值为( A )。
A.520 B.510 C.500 D.5406.不受极端变量值影响的平均数是( D )。
A.算术平均数B.调和平均数C.几何平均数D.众数7.有20个工人看管机器台数资料如下:2,5,4,4,3,4,3,4,4,2,2,4,3,4,6,3,4,5,2,4,如按以上资料编制频数分布数列应采用(A )。
A.单项式分组B.等距分组C.不等距分组D.以上几种分组均可以8.若无季节变动,则季节比率应为( B )。
A.0 B. 1 C.大于1 D. 小于19.如果一个定性的变量有m类,则要引进( C )个虚拟变量。
A.mB.m+1C.m-1D.无法判断10.第一组工人的平均工龄为5年,第二组为7年,第三组为10年,第一组工人数占总数的20%,第二组占60%,则三组工人的平均工龄为( B )A.8年B.7.2年C.5年D.7.8年11.某企业2007年各种产品的产量比2006年增长了8%,总生产费用增长了12%,则该厂2007年单位成本( D )A.减少了0.62%B.增加了0.62%C.减少了3.7%D.增加了3.7%12.相关系数r与斜率b2的符号( A )。
试分别计算该商品在两个市场上的平均价格。
(20分)09.7 11.7 12.7
2014.1
合计
50
—
3870 —
4312
乙班学生的标准差()()分=
乙29.924.8650
4312
2
===
-∑∑f
f
x x σ
甲、乙两个生产小组, 甲组平均每个工人的日产量为36 件, 标准差为件; 乙组工人日产量资料如下:
第三类:采用简单重复抽样的方法计算平均数(成数)的抽样平均误差;根据要
3.某工厂有2000个工人,用简单重复方法抽出其100个工人作为样本
出平均产量560件,标准差点32.45件.
要求:(1)计算抽样平均平均误差;
(2)以95.45%(z=2)的可靠性估计该厂工人的月平均产量及总产量区间.(20分)07.1
解: (1)
25
.3
100
45
.
32
=
=
n
x
σ
μ=
(2)
49.6
245
.3
2=
⨯
=
=
∆μz
x
13.1
(
19. 某单位按简单随机重复抽样方式抽取40 名职工,对其业务情况进行考核,核成绩平均分数77分,标准差为1 0.54分.试以95. 45%的概率保证程度( Z= 2)断全体职工业务考试成绩的区间范围。
( 1 5分)11.7
第四类:计算相关系数;建立直线回归方程并指出回归系数的含义;利用建立的方程预测因变量的估计值。
04.7 05.1 06.1 06.7 07.1 08.7 09.7 11.1 11.7 14.1
1.根据某地区历年人均收入(元)与商品销售额(万元)资料计算的有关数据如下:(x 代表人均收入,y 代表销售额):
计算:(1)建立以商品销售额为因变量的直线回归方程,并解释回归系数的含义;
(2)若2010年人均收为24000元,试推算该年的商品销售额。
06.7
回归系数b 表示当人均收人每增加一元时,商品销售额平均增加0.92万元。
(2)预测2010年商品销售额 x=24000代入方程
)(08.220532400092.092.2692.092.26万元=⨯+-=+-=x y c
2.为研究产品销售额和销售利润之间的关系,某公司对所属地10家企业进行调查,设产品销售额为x(万元), 销售利润为y(万元).对调查资料进行进行整理和计算,其结果如下: n=10
x ∑=795 y ∑=1065 2
x
∑=72925
xy ∑=93200 ∑=1214752
y
要求:(1)计算销售额与销售利润之间的相关系数;
(2)配合销售利润对销售额的直线线回归方程.(15分)07.1
解: (1)计算相关系数;
要求 :( 1)建立销售利润倚可比产品成本降低率的直线回归方程,预测可比
(2 )计算学习时间和学习成绩之间的相关系数,并解释相关的密切程度和方向。
(要求写出公式和计算过程,结果保留两位小
5.某企业第二季度产品产量与单位成本资料如下:
月份产量(千件) 单位成本
(元)
4 3 73
14.7
第五类:计算数量指数及质量指数并同时指出变动绝对值、计算加权算术
平均数指数。
04.7 05.1 06.1 06.7 08.1 08.7 09.1 10.7 11.1 12.1 12.7 13.7
1.某企业生产两种产品的有关资料如下:
要求:(1)计算两种产品产量总指数以及由于产量变动使总成本变动的绝对额;
(2)计算两种产品单位成本总指数以及由于单位成本变动使总成本变动的绝对额。
06.7
(1)产量总指数:
%3.13032000
4300015002020010200020300100
10==⨯+⨯⨯+⨯==
∑∑q
p q p K q
由于产量变动使总成本变动的绝对额:
)(11000320004300000
1
元=-=-∑∑p q
p q
(2)单位成本指数:
%05.10643000
4560020002030010200021300121
011==⨯+⨯⨯+⨯==
∑∑q
p q p K p
由于单位成本变动使总成本变动的绝对额:
)(260043000456001
01
1元=-=-∑∑q
p q p
2. 某企业生产甲、乙两种产品,基期和报告期的产量、单位成本资料如下:
19. 某市场对两类商品的收购价格和收购额资料如下: 试求收购价格总指数、收购额总指数。
(1 5 分)12.7
2014.1
要求计算:(1)三种商品销售量总指数;
(2 )销售量变化对销售收人的影响额.05.1
4、某企业产品总成本和产量资料如下:
总成本(万元)产品增长(%)产品名称
基期报告期
甲100 120 20
5.某集团公司销售的三种商品的销售额及价格提高幅度资料如下:
商品种类单位商品销售额(万元) 价格提高%
基期报告期
甲条10 11 2
乙件15 13 5
丙块20 22 0
试求价格总指数和销售额总指数。
(15分)学习指导书p224 09.1
5.某企业产品总成本和产量资料如下:
试计算总成本指数、产量指数及产品单位成本总指数。
04.7
第六类:根据资料计算动态数列序时平均数(相对数与平均数动态数列);利用平均发展速度指标公式计算期末水平。
04.7 05.1 06.7 07.7 08.1
10.7 12.7 13.1
1.某地区历年粮食产量如下:
要求:(1)试计算各年的环比发展速度及年平均增长量;
(2)如果从2004年以后该地区的粮食生产以10%的增长速度发展,预计到2010年该地区的粮食产量将达到什么水平? 06.7 07.7
解:
(1)计算结果如下表:
(2)如果从2004年以后该地区的粮食生产以10%的增长速度发展,预计到2010年该地区的粮食产量将达到;
某地区历年粮食产量如下:
要求:(1)试计算各年的逐期增长量及年平均增长量。
(2)如果从2006年起该地区的粮食生产以10%的增长速度发展,预计到2010年该地区的粮食产量将达到什么水平?13.1
10.7 12.7
2.某百货公司各月商品销售额及月末库存资料如下:
3月4月5月6月
4.某工业企业的调查资料如下表,试运用动态指标的相互关系:(1)
数列的发展水平和表中所缺的动态指标;(2)以1990年为基期,计算平均发展速度。
(要求写出公式和计算过程)05.1
14.7。