大学物理实验PN结正向压降温度特性的研究实验报告
- 格式:pdf
- 大小:48.89 KB
- 文档页数:4

PN结正向压降与温度关系的研究实验报告实验报告:PN结正向压降与温度关系的研究实验摘要:本实验旨在研究PN结正向压降与温度之间的关系。
通过改变PN结的温度,测量对应的正向压降,并分析得出结论。
实验结果表明,PN结的正向压降与温度呈正相关关系。
引言:PN结是半导体器件中的重要组成部分,其正向压降是衡量PN结导通能力的重要参数。
正向压降与温度之间的关系对于理解和优化半导体器件的性能具有重要意义。
因此,研究正向压降与温度之间的关系对于半导体器件的应用具有重要的理论和实际意义。
实验材料和方法:1.实验材料:PN结样品、测量仪器(包括数字万用表、恒流源等)。
2.实验方法:a.搭建实验电路,将PN结样品连接到恒流源,设置合适的电流值。
b.测量不同温度下PN结的正向压降,记录实验数据。
c.对实验数据进行处理和分析,得出结论。
实验结果:在实验过程中,我们固定了恒流源的电流值为I=10mA。
通过改变PN结的温度,在不同温度下测量了对应的正向压降数据,将实验数据整理如下:温度(℃)正向压降(V)250.6300.65350.68400.7450.72500.75550.78600.82讨论和结论:实验结果表明,PN结的正向压降与温度呈正相关关系。
这可能是由于温度升高导致了载流子在PN结中的增加,进而导致了正向电流的增加,从而使正向压降增加。
此外,温度升高还可能导致半导体材料的电阻变化,进而影响了正向压降。
综上所述,通过对PN结正向压降与温度关系的研究实验,我们发现正向压降与温度呈正相关关系。
这对于理解PN结的导通特性和优化半导体器件的性能具有重要意义。
附录:实验数据表格温度(℃)正向压降(V) 250.6300.65350.68400.7450.72500.75550.78。

实验题目:PN 结正向压降温度特性的研究实验目的:了解PN 结正向压降随温度变化的基本关系式。
在恒流供电条件下,测绘PN 结正向压降随温度变化曲线,并由此确定其灵敏度和被测PN 结材料的禁带宽度。
学习用PN 结测温的方法。
实验原理:理想PN 结的正向电流I F 和压降V F 存在近似关系:)exp(kTqV Is I FF = 其中q 为电子电荷,k 为玻尔兹曼常数,T 为绝对温度,I S 为反向饱和电流:])0(ex p[kTqV CT Is g r -=由上面可以得到: 11)0(n r F g F V V InT q kT T Ic In q k V V +=-⎪⎪⎭⎫ ⎝⎛-= 其中()rn F g InT qKTV T IcIn q k V V -=⎪⎪⎭⎫ ⎝⎛-=11)0(在上面PN 结正向压降的函数中,令I F =常数,那么V F 就是T 的函数。
考虑V n1引起的线性误差,当温度从T 1变为T ,电压由V F1变为V F : []rn F g g F T T q kT T T V V V V ⎪⎪⎭⎫ ⎝⎛---=1111)0()0( )(111T T TV V V F F F -∂∂+=理想()[]()r T T q kT T V V V T T r q k T V V V V F g g F g F 1111111)0()0(----=-⎥⎦⎤⎢⎣⎡---+=理想两个表达式相比较,有:()r F T TLn q kT T T r q k V V )(11+--=-=∆理想 综上可以研究PN 结正向压降温度特性。
实验内容:1、求被测PN 结正向压降随温度变化的灵敏度S (mv/℃)。
作∆V —T 曲线(使用Origin 软件工具),其斜率就是S 。
2、估算被测PN 结材料硅的禁带宽度E g (0)=qV g (0)电子伏。
根据(6)式,略去非线性,可得T S T V T TV T V V s F F S F g ∆⋅++=∆+=)2.273()0()( ∆T=-273.2K ,即摄氏温标与凯尔文温标之差。

大学物理实验教案实验名称:PN 结正向电压温度特性的测定1 实验目的1)了解PN 结正向电压随温度变化的基本规律。
2)掌握用计算机测绘恒流条件下PN 结正向电压随温度变化的关系曲线。
3)确定PN 结的测温灵敏度。
2 实验仪器科学工作室接口、放大器、恒流源、计算机3 实验原理3.1实验原理PN 结是半导体器件的核心。
在P (或N )型半导体中,用杂质补偿的方法将其中一部分材料转变成N (或P )型,这样,在两种材料交界处就形成了PN 结,它保持了两种材料之间晶格的连续性。
P 区多子空穴比N 区少子空穴浓度大,空穴由P 区向N 区扩散,并与N 区的多子自由电子复合,在N 区产生正离子的电荷区;N 区多子自由电子比P 区少子自由电子浓度大,自由电子由N 区向P 区扩散,并与P 区的多子空穴复合,在P 区产生负离子的电荷区。
P 区和N 区的电荷区之间形成电场,在此电场作用下产生与扩散运动相反的情况,它阻止扩散运动的进一步加强。
最终形成两种运动的动态平衡。
我们把这个空间电荷区叫PN 结,有时也叫作耗尽层。
根据半导体理论,通过PN 结的正向电流e I IkT qV s f =(1) 式中:I f ——正向电流(mA );V f ——正向压降(V );I s ——反向饱和电流(mA );q电子电量(e );k ——波尔兹曼常数;T ——热力学温度(K )。
而:e T I kT V goq B A s -=(2)式(2)中:V go ——能带间隙电压(V );A 、B ——由PN 结工艺结构所决定的常数。
由(1)、(2)式经整理后,PN 结正向压降的温度灵敏度S 为:)(q kB T f go dT f d S V V V +--== (3)根据这一特性,PN 结可作为温度传感器来使用。
3.2实验方法本实验通过电加热的方法提供给PN 结一个温度可以变化的热源,利用精确的温度传感器测量温度。
把待测的PN 结放置热源中,并利用恒流源给定待测PN 结一个恒定电流,PN 结两端则接入一高稳定放大器进行电压放大后,连接到自定义电压传感器来测量电压。
PN结正向压降与温度关系的研究和应用一、实验目的1、了解PN结正向压降随温度变化的基本关系式。
2、在恒流条件下,测绘PN结正向压降随温度变化的曲线,并由此确定其灵敏度和被测PN结材料的禁带宽度。
3、学习用PN结测温的方法。
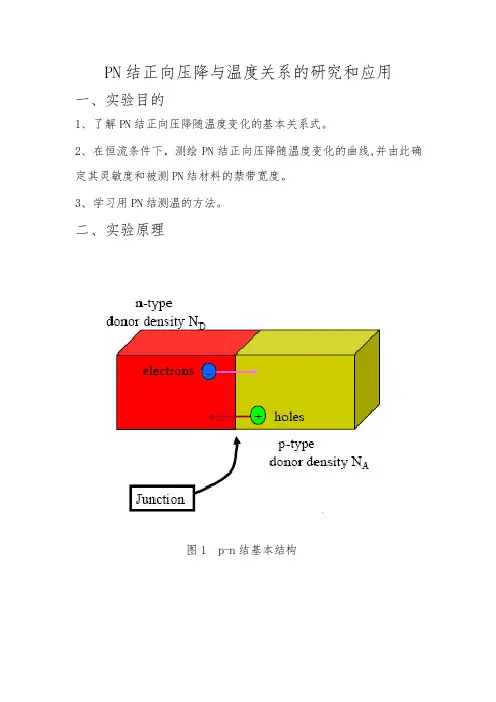
二、实验原理图1 p-n结基本结构价带顶部激发电子到导带相当于共价键上缺少一个电子而出现一个空位置,而在晶格间隙出现一个导电电子。
空状态带有正电荷,叫“空穴”。
空穴能导电,具有有效质量。
**n p m m -=3.PN结的形成当p型半导体和n型半导体接触在一起时,在两者的交界面处存在着一个过渡区,通常称为p-n结.三、实验仪器•TH-J型PN结正向压降与温度关系测量仪•五芯电缆一根四、实验步骤1、实验系统的连接控制电流开关置“关”的位置,此时加热指示灯不亮,接上加热电源线及信号传输线将样品室与仪器相连。
注意定位标记。
拆除时应拉插头外套不可硬拉和转动。
2、V ~T 的测量和调零 开启仪器背部的电源开关,加热数分钟后,将“测量选择”开关(以下简称K )拔到 档,由“ 调节”使 =50µA ,记下当时温度值。
将K 拔到△V 档,由 “△V 调零”使△V=0。
3、 测曲线开启加热电源(指示灯亮)加热电流范围0.2~0.3A ,并记录△V 和T 值,按每改变10mV 立即读取相应T 值。
为使整个实验符合热力学条件,在实验过程中升温速度要慢。
4、求被测PN 结正向压降随温度变化的灵敏度S ( )F/mv C作 曲线,求斜率S 。
五、实验数据记录V(mv)-5 -10 -15 -20 -25 -30 -35 -40 -45 -50 -55 -60 -65-70 T( C) 24.1 26.4 28.6 30.8 33.0 35.2 37.4 39.5 41.7 43.8 46.0 48.2 50.3 52.4实验起始温度: 21.4℃工作电流: = 50µA 起始温度时的正向压降: 573mV六、数据处理过程及结果、结论s T =FI ()F R V T =七、注意事项1、仪器连接线的芯线较细,所以使用时应注意,不可用力过猛。

PN 结正向电压温度特性研究一、实验目的(1)了解PN 结正向电压随温度变化的基本规律。
(2)在恒流供电条件下,测绘PN 结正向电压随温度变化的关系图线,并由此确定PN 结的测温灵敏度和被测PN 结材料的禁带宽度。
二、实验仪器PN 结正向特性综合实验仪、DH-SJ5温度传感器实验装置。
三、实验原理1、测量PN 结温度传感器的灵敏度 由半导体理论可知,PN 结的正向电流I F 与正向电压V F 满足以下关系:I F =I n (ⅇqV FkT−1)(1)式(1)中I n 是反向饱和电流,T 是热力学温度,q 是电子的电量。
由于在常温(例如300K )时,kT/q 约为0.026V ,而PN 结正向电压约为十分之几伏,所以ⅇ^((qV_F)/kT)≫1,故式(1)中括号内的−1项完全可以忽略,于是有: I F =I n ⅇqV F kT(2)其中,I n 是与PN 结材料禁带宽度及温度等有关的系数,满足以下关系:I n =CTγⅇqV g0kT(3)式(3)中C 为与PN 结的结面积、掺杂浓度等有关的常数,k 为玻尔兹曼常数,γ在一定温度范围内也是常数,V g0为热力学温度0K 时PN 结材料的导带底与价带顶的电势差,对于给定的PN 结,V g0是一个定值。
将式(3)代入式(2),两边取对数,整理后可得:V F =V g0−(k q ln C I F )T −kTqln T γ=V 1+V nr (4)其中V 1=V g0−(k q ln CI F)T (5) V n r =−kTqln T γ (6)根据式(4),对于给定的PN 结材料,令PN 结的正向电流I F 恒定不变,则正向电压V F 只随温度变化而变化,由于在温度变化范围不大时,V n r 远小于V 1,故对于给定的PN 结材料,在允许的温度变化范围内,在恒流供电条件下,PN 结的正向电压V F 几乎随温度升高而线性下降,即 V F =V g0−(k q ln CI F)T(7)为了便于实际使用对式(7)进行温标转换,确定正向电压增量∆V [与温度为0℃时的正向电压比较]与用摄氏温度表示的温度之间的关系。

PN结正向压降与温度关系的研究和应用实验报告摘要:本实验通过测量PN结正向偏置情况下的正向压降随温度的变化,研究PN结的温度特性,并探索其在实际应用中的可能的应用。
引言:PN结是半导体器件中最基本的结构之一,其正向特性在电子学领域具有重要的应用价值。
而PN结的温度特性对于器件的工作稳定性和可靠性有较大的影响。
因此,研究PN结的温度特性,尤其是正向压降与温度的关系,对于提高器件性能有着重要意义。
实验目的:1.研究PN结的温度特性,特别是正向压降随温度的变化规律;2.探索PN结温度特性相关的应用,例如热敏电阻等。
实验原理:PN结在正向偏置情况下,通过正向电流使得P区载流子与N区载流子复合,产生电压降。
根据热力学原理,温度升高会提供更多的热能,促使载流子的热激发增加,从而降低正向电压的阻挡力。
因此,PN结正向压降与温度呈负相关。
实验步骤:1.搭建实验电路:将PN结与电源和电流测量仪连接,确保电路连接正确。
2.在实验装置中设置好温度传感器,与PN结接触。
3.调节电源的正向电流,并分别测量不同温度下的正向压降和电流。
4.依次调节不同温度下的电流,重复步骤3,记录数据。
实验结果:将测得的正向电流和压降数据制成表格,并绘制电压-温度曲线和电流-温度曲线。
讨论:通过分析实验结果,可以发现PN结的正向压降随着温度的升高而逐渐降低,且呈现较大的线性关系。
这与实验原理的推测相符合。
应用:基于PN结正向压降与温度的关系,我们可以将其应用于热敏电阻的制备和温度测量。
热敏电阻可以根据PN结的特性,根据温度的变化来改变电阻值,从而实现温度的感应和测量。
这在实际工业控制和家用电器中具有广阔的应用前景。
结论:通过本实验研究PN结的温度特性,我们发现PN结的正向压降随着温度升高而逐渐降低,并且可以将该特性应用于热敏电阻的制备和温度测量中。
实验结果对于提高PN结的性能和应用具有重要参考价值。

实验题目:PN 结正向压降温度特性的研究 实验目的:1) 了解PN 结正向压降随温度变化的基本关系式。
2) 在恒流供电条件下,测绘PN 结正向压降随温度变化曲线,并由此确定其灵敏度和被测PN 结材料的禁带宽度。
3) 学习用PN 结测温的方法。
实验原理:理想PN 结的正向电流I F 和压降V F 存在如下近似关系 )exp(kTqV Is I FF = (1) 其中q 为电子电荷;k 为波尔兹曼常数;T 为绝对温度;Is 为反向饱和电流,它是一个和PN 结材料的禁带宽度以及温度等有关的系数,可以证明 ])0(ex p[kTqV CT Is g r-= (2)其中C 是与结面积、掺质浓度等有关的常数:r 也是常数;V g (0)为绝对零度时PN 结材料的导带底和价带顶的电势差。
将(2)式代入(1)式,两边取对数可得 11)0(n r Fg F V V InT q kT T I c In qkV V +=-⎪⎪⎭⎫ ⎝⎛-= (3) 其中这就是PN 结正向压降作为电流和温度函数的表达式。
令I F =常数,则正向压降只随温度而变化,但是在方程(3)中,除线性项V 1外还包含非线性项V n1项所引起的线性误差。
设温度由T 1变为T 时,正向电压由V F1变为V F ,由(3)式可得[]rn F g g F T T q kT T T V V V V ⎪⎪⎭⎫⎝⎛---=1111)0()0( (4) 按理想的线性温度影响,VF 应取如下形式: )(111T T TV V V F F F -∂∂+=理想 (5)T V F ∂∂1等于T 1温度时的TVF ∂∂值。
由(3)式可得r qk T V V T V F g F ---=∂∂111)0((6)所以()[]()r T T q kT T V V V T T r q k T V V V V F g g F g F 1111111)0()0(----=-⎥⎦⎤⎢⎣⎡---+=理想 (7)由理想线性温度响应(7)式和实际响应(4)式相比较,可得实际响应对线性的理论偏差为()r F T TLn q kT T T r q k V V )(11+--=-=∆理想 (8)设T 1=300°k ,T=310°k ,取r=*,由(8)式可得=,而相应的V F 的改变量约20mV ,相比之下误差甚小。


实验 pn 结正向压降温度特性研究【实验目的】1、了解pn 结正向压降随温度变化的基本关系式.2、在恒定正向电流下,测绘pn 结正向压降随温度变化曲线,并由此确定其灵敏度.3、学习用pn 结测温的方法.【实验仪器】1、DH-PN-1型pn 结正向压降温度特性实验仪【实验原理】1、pn 结在一块完整的硅或锗上用不同的工艺掺入杂质,使得其一半成为P 型半导体,而另一半成为N 型半导体,那么,在这两种半导体的交界处就会形成pn 结.在P 型与N 型半导体结合后,由于P 型半导体具有较高浓度的空穴,而N 型半导体具有较高浓度的自由电子,在他们交界处的两边就出现了电子与空穴的浓度差别.从而,电子与空穴都要朝着较低浓度的方向扩散.这种扩散作用,使得在P 、N 交界处之间形成了具有一定大小的扩散电流.另一方面,由于P 型半导体中空穴的流失,使得P 型半导体中留下了一定量带负电的离子;而N 型半导体中由于电子的流失,使得其中留下了一定量的正离子.由于正负电荷之间的相互作用,使得在交界薄膜中形成了从N 型半导体指向P 型半导体的空间电场.而空间电场的形成使得一部分的空穴与电子沿与扩散相反的方向运动,形成漂移电流.空穴与自由电子的扩散使得空间电场增强,而空间电场的增强却又抑制空穴与电子的扩散,从而,在一段时间之后,扩散电流将与漂移电流达到动态平衡.而在P 型与N 型半导体的两侧则会留下不能自由移动的离子薄层,而这个离子薄层在P 、N 半导体交界面附近所构成的过渡区(空间电荷区), 图1 PN 结 即称为pn 结.2、pn 结的正向压降温度特性根据pn 结理论, pn 结的伏安特性可表达如下:01F qU kT F I I e ⎛⎫=- ⎪⎝⎭(1-1)式中F I 为通过pn 结的正向电流, F U 为其正向电压, 0I 为反向饱和电流; q 为电子的电荷量, T 为绝对温度231.3810/k J K -=⨯是玻尔兹曼常量当正向电压0.1F U V >时, 3.9501FqU kTee ≈≈,故上式可近似为0FqU kTF I I e= (1-2)由式(1-2)得0ln ln FqU kTF I I e=⇒ 0ln ln F F qUI I kT =+又 0gqU kTI BT eγ-=⇒ ()ln ln F F g q I BT U U kT γ=+-ln F g F kT BT U U q I γ⎛⎫=- ⎪⎝⎭(1-3) 式(1-3)即为pn 结两端正向电压与其温度、通过电流之间的关系.其中, g U 为0K 时材料的导带底与价带顶间的电势差, B 是与温度无关的实验常数, T γ是与温度有关的函数项, γ为与热激发所引起的电子迁移率有关的系数.取F I 为一常数,则(1-3)式转化为通过pn 结的电压F U 与pn 结温度T 之间的关系. 对F U 取一阶导数,得ln FF dU k BT q I dTγγ⎛⎫=-+ ⎪⎝⎭ (1-4) FdU dT即代表了F U T -图线的斜率,由(1-4)可以看出, 斜率为负,F U 随温度T 的上升而下降. 对F U 取二阶导数,得22F d U k qT dTγ=- (1-5) 其中,231.3810k -=⨯、191.6010q -=⨯,取 3.4γ=,293.15T =得,262 1.0100F d U k qT dTγ-=-≈⨯→ 即, F U T -图线的斜率可近似认为一常数, F U T -可近似认为是一条直线. 根据(1-3)式ln ln ln F g g F F kT kT kT BT B U U U T q I q I q γγ⎛⎫=-=-- ⎪⎝⎭(1-6) 设,温度为1T 时,电势差为1U1111ln ln g FkT kT BU U T qI qγ=--又 ln ln g F F kTkT BU U T qI qγ-=+得 ()1111ln g g F T kT T U U U U Tq T γ⎛⎫=--- ⎪⎝⎭(1-7) 由上推导可知, F U 应与T 呈线性关系,故设()()11FF U U T U T T T ∂=+-∂()1()gFF U U k U T T T qγ-=---()()11gF F UU T k U T T Tq γ-=--- (1-8)令 ()()11111ln kT T k U U T U T T q q T γγ⎛⎫=-=--+⎪⎝⎭(1-9) 设300T K =、1310T K =,取 3.4γ=可得0.048U mV =,而相应的正向压降则改变了20mV ,差值约为417倍,相比之下,误差甚小.不过当温度变化过大之后F U T -图线的线性误差将有所递增.由于F U 与T 呈很好的线性相关性,故可利用F U 的细微变化来测量当前环境的温度.这也是温敏二极管测温的基本原理.【实验步骤】1、打开pn 结正向压降温度特性实验仪并调节加热电流值为零,记录起始温度.2、将“测量选择”开关调节到F I 档,调节F I 旋钮,使得面板上F I 的值为零.3、将“测量选择”开关调节到F U 档,记下初始时的F U 值.4、将“测量选择”开关调节到U ,调节调零旋钮,使得0U =.5、调节加热电流为0.500A ,并记录所对应的U 和T 值.当U 每改变10mV 时记录一次T 值.直到pn 结温度达到大约100℃为止.6、画出U T -图像,并求被测pn 结正向压降随温度变化的灵敏度()/S mV ℃. 8、估算被测pn 结材料的禁带宽度g g E qU =.9、实验结束,收拾仪器.注意事项1、加热装置的温升不应超过120℃,长期的过热使用,将造成接线老化,甚至脱焊.2、加热电流不应大于0.500A ,若长期使加热电流过大,会使得仪器未来的加热效率变低.3、使用完毕后即应切断电源,以避免长时间加热引起的安全事故.【实验数据整理】表一:-U T 测量数据/U mV0 -10 -20 其中,初始正向电压0667U mV =.【数据处理过程及结论】数据处理1、根据数据,画出U T -图像如下d e t UT通过线性拟合,得到 2.0337.75U T =-+,20.99995R =2、由 2.0337.75U T =-+得到被测pn 结正向压降随温度变化的灵敏度为: 2.03/S mV =-℃.3、被测pn 结材料的禁带宽度()0g g E qU q U S T ==-[667 2.03(18.2273.15)]q =+⨯+ 1.26eV ≈实验结论 1、通过本次实验,测得pn 结两端正向电压与其上的温度变化呈很好地线性关系.判断是因为温度升高导致P 、N 型半导体更容易激发出空穴与自由电子.加正向电压时,由于载流子浓度的上升,使得漂移作用更加明显,pn 结的导电能力增强.宏观上表现为pn 结的电阻降低,故在相同的正向电流F I 下,温度上升将导致pn 结的正向电压F U 下降.故以此推测:由于在温度过高的情况下, pn 结内载流子浓度的迅速增加(温度上升,使得空穴与自由电子的运动速度上升,在一定程度后,它们将有足够的能量撞击半导体分子,使得共价键被破坏,逸出更多的电子),这将导致pn 结的正电压迅速下降,故原理中的线性推导在温度过高时将不在适用,则温敏二极管不能准确测量较高的温度.2、通过本次实验,测得待测pn 结正向压降随温度的变化关系具体可表示为2.0337.75U T =-+其正向电压随温度变化的灵敏度 2.03/S mV =-℃.3、通过本次实验测得被测pn 结材料的禁带宽度 1.26g E eV ≈.。

⼤学物理实验PN结正向压降与温度特性的研究实验报告(完整)PN 结正向压降与温度特性的研究⼀、实验⽬的1.了解PN 结正向压降随温度变化的基本关系式。
2.在恒流供电条件下,测绘PN 结正向压降随温度变化曲线,并由此确定其灵敏度和被测PN 结材料的禁带宽度。
3.学习⽤PN 结测温的⽅法。
⼆、实验原理理想PN 结的正向电流I F 和压降V F 存在如下近似关系)exp(kTqV Is I FF = (1)其中q 为电⼦电荷;k 为波尔兹曼常数;T 为绝对温度;Is 为反向饱和电流,它是⼀个和PN 结材料的禁带宽度以及温度等有关的系数,可以证明])0(ex p[kTqV CT Is g r -= (2)(注:(1),(2)式推导参考刘恩科半导体物理学第六章第⼆节)其中C 是与结⾯积、掺质浓度等有关的常数:r 也是常数;V g (0)为绝对零度时PN 结材料的导带底和价带顶的电势差。
将(2)式代⼊(1)式,两边取对数可得11)0(n r F g F V V InT q kT T IcIn q k V V +=--= (3)其中()rn F g InT qKTV T Ic In q k V V -=???? ?-=11)0(这就是PN 结正向压降作为电流和温度函数的表达式,它是PN 结温度传感器的基本⽅程。
令I F =常数,则正向压降只随温度⽽变化,但是在⽅程(3)中,除线性项V 1外还包含⾮线性项V n1项所引起的线性误差。
设温度由T 1变为T 时,正向电压由V F1变为V F ,由(3)式可得[]rn F g g F T T q kT T T V V V V---=1111)0()0( (4)按理想的线性温度影响,VF 应取如下形式:)(111T T TV V V F F F -??+=理想(5) TV F ??1等于T 1温度时的T V F ??值。
由(3)式可得r qk T V V T V F g F ---=??111)0( (6)所以()[]()r T T q kT T V V V T T r q k T V V V V F g g F g F 1111111)0()0(----=----+=理想(7)由理想线性温度响应(7)式和实际响应(4)式相⽐较,可得实际响应对线性的理论偏差为()r F T T Ln q kT T T r q k V V )(11+--=-=?理想(8)设T 1=300°k ,T=310°k ,取r=3.4*,由(8)式可得?=0.048mV ,⽽相应的V F 的改变量约20mV ,相⽐之下误差甚⼩。

PN 结正向压降与温度特性的研究一、实验目的1. 了解PN 结正向压降随温度变化的基本关系式。
2. 在恒流供电条件下,测绘PN 结正向压降随温度变化曲线,并由此确定其灵敏度和被测PN 结材料的禁带宽度。
3. 学习用PN 结测温的方法。
二、实验原理理想PN 结的正向电流I F 和压降V F 存在如下近似关系)exp(kTqV Is I FF = (1) 其中q 为电子电荷;k 为波尔兹曼常数;T 为绝对温度;Is 为反向饱和电流,它是一个和PN 结材料的禁带宽度以及温度等有关的系数,可以证明])0(ex p[kTqV CT Is g r -= (2)(注:(1),(2)式推导参考 刘恩科 半导体物理学第六章第二节)其中C 是与结面积、掺质浓度等有关的常数:r 也是常数;V g (0)为绝对零度时PN 结材料的导带底和价带顶的电势差。
将(2)式代入(1)式,两边取对数可得11)0(n r F g F V V InT q kT T IcIn q k V V +=-⎪⎪⎭⎫ ⎝⎛-= (3) 其中()rn F g InT qKTV T Ic In q k V V -=⎪⎪⎭⎫ ⎝⎛-=11)0(这就是PN 结正向压降作为电流和温度函数的表达式,它是PN 结温度传感器的基本方程。
令I F =常数,则正向压降只随温度而变化,但是在方程(3)中,除线性项V 1外还包含非线性项V n1项所引起的线性误差。
设温度由T 1变为T 时,正向电压由V F1变为V F ,由(3)式可得[]rn F g g F T T q kT T T V V V V ⎪⎪⎭⎫⎝⎛---=1111)0()0( (4) 按理想的线性温度影响,VF 应取如下形式:)(111T T TV V V F F F -∂∂+=理想 (5) TV F ∂∂1等于T 1温度时的T V F ∂∂值。
由(3)式可得r qk T V V T V F g F ---=∂∂111)0( (6) 所以()[]()r T T q kT T V V V T T r q k T V V V V F g g F g F 1111111)0()0(----=-⎥⎦⎤⎢⎣⎡---+=理想(7)由理想线性温度响应(7)式和实际响应(4)式相比较,可得实际响应对线性的理论偏差为()r F T T Ln q kT T T r q k V V )(11+--=-=∆理想 (8)设T 1=300°k ,T=310°k ,取r=3.4*,由(8)式可得∆=0.048mV ,而相应的V F 的改变量约20mV ,相比之下误差甚小。
PN结正向压降温度特性的研究实验报告实验报告:PN结正向压降温度特性的研究引言:PN结是指由P型半导体和N型半导体的结合处所形成的一个具有整流特性的半导体器件。
在正向偏置的情况下,PN结会产生一个较小的电压降,这主要是由载流子在PN结中的扩散和漂移引起的。
而随着电流的增加,PN结会产生一定的热量,这会导致PN结的温度升高。
本实验旨在研究PN结正向压降与温度的关系,进一步了解PN结的温度特性。
实验目的:1.研究PN结正向压降随温度的变化规律;2.了解PN结在不同温度下的工作情况;3.探究PN结的温度特性。
实验器材:1.PN结二极管;2.恒流源;3.电源;4.温度控制装置;5.万用表。
实验步骤:1.将PN结二极管连接到恒流源和电源上,确保连接正确;2.打开电源,使PN结正常导通;3.利用温度控制装置,逐步增加PN结的温度,记录温度与正向压降之间的对应关系;4.根据实验结果绘制PN结正向压降与温度变化的曲线。
实验结果:温度(摄氏度)正向压降(V)200.7300.68400.67500.65600.64数据处理与分析:根据实验结果,可以观察到PN结的正向压降随着温度的升高而略微减小。
这是由于温度的升高会增加载流子的扩散速度以及PN结内的载流子浓度,使得电流更容易通过PN结,从而使得正向压降减小。
这种现象在实际应用中也被广泛利用,例如在高温环境下,PN结可以更好地工作。
结论:本实验研究了PN结正向压降随温度的变化规律。
实验结果表明,PN结正向压降随着温度的升高而略微减小。
这一结果有助于我们更好地了解PN结的温度特性,并在实际应用中进行合理的设计和选择。
此外,本实验还为进一步研究PN结的温度特性提供了一定的参考和基础。
致谢:感谢实验设备的提供以及一直以来对我们实验工作的指导和支持。
同时,也感谢实验组成员的共同努力和配合,使得实验能够顺利进行并取得实验结果。
pn结正向压降与温度关系的研究实验报告.doc
实验原理:p-n结是半导体器件中最基本的一种,其具有单向导电性能,因此在正向
偏置时,电流可流通,反向偏置时电流不能流通。
在实际应用中,p-n结的正向偏置电压
往往是一个重要的参数,因此研究正向压降随着温度的变化规律有着重要的意义。
实验步骤:
1.准备相应的实验材料:p-n结柱、万用表、稳压源、温度计、热电偶、直流电源等。
2.将p-n结柱插入稳压源的输出端,接通电源,并将万用表的正负极分别接在正负极
之间,记录下正向偏置的电压值。
3.将热电偶紧贴p-n结表面,记录下当前的温度值。
4.分别改变p-n结的温度值,并记录正向偏压下的电压值,得到多组数据。
5.根据实验数据,绘制电压-温度曲线图,进行分析。
实验数据记录:
| 温度(℃)| 正向偏压(V)|
| -------- | -------- |
| 20 | 0.35 |
| 30 | 0.32|
| 40| 0.29|
| 50| 0.26|
| 60| 0.23|
数据处理:
将所得数据画成图表,可以看出正向偏压随着温度的升高而逐渐降低。
结论:
从实验结果可以看出,p-n结正向偏压随着温度的升高而逐渐降低,这是由于随着温
度升高,半导体材料中的自由载流子浓度会增加,这会导致势垒高度的减小,从而使正向
偏压下的电压降低。
因此,在半导体器件的实际应用中,需要注意温度变化对其性能的影响,合理的散热设计可以有效提高器件的工作可靠性。
PN 结正向压降与温度关系的研究实验报告一、实验目的〔1〕了解PN 结正向压降随温度变化的根本关系,测定PN 结F F V I -特性曲线及玻尔兹曼常数;〔2〕测绘PN 结正向压降随温度变化的关系曲线,确定其灵敏度及PN 结材料的禁带宽度;〔3〕学会用PN 结测量温度的一般方法。
二、实验仪器SQ-J 型PN 结特性测试仪,三极管〔3DG6〕,测温元件,样品支架等。
三、实验原理1.PN 结F F V I -特性及玻尔兹曼常数k 的测量:由半导体物理学中有关PN 结的研究可以得出PN 结的正向电流F I 与正向电压F V 满足以下关系F I =s I 〔e*p kTeV F -1〕⑴ 式中e 为电子电荷量、k 为玻尔兹曼常数,T 为热力学温度,s I 为反向饱和电流,它是一个与PN 结材料禁带宽度及温度等因素有关的系数,是不随电压变化的常数。
由于在常温〔300K 〕下,kT/q=0.026,而PN 结的正向压降一般为零点几伏,所以e*p kTeV F ",1上式括号的第二项可以忽略不计,于是有 kT eV Is I F F exp=⑵ 这就是PN 结正向电流与正向电压按指数规律变化的关系,假设测得半导体PN 结的F F V I -关系值,则可利用上式以求出e/kT.在测得温度T 后,就可得到e/k 常数,将电子电量代入即可求得玻尔兹曼常数k 。
在实际测量中,二极管的正向F F V I -关系虽能较好满足指数关系,但求得的k 值往往偏小,这是因为二极管正向电流F I 中不仅含有扩散电流,还含有其它电流成份。
如耗尽层复合电流.、外表电流等。
在实验中,采用硅三极管来代替硅二极管,复合电流主要在基极出现,三极管接成共基极线路〔集电极与基极短接〕,集电极电流中不包含复合电流。
假设选取性能良好的硅三极管,使它处于较低的正向偏置状态,则外表电流的影响可忽略。
此时集电极电流与发射极—基极电压满足⑵式,可验证该式,求出准确的e/k 常数。
实验题目: PN 结正向压降温度特性的研究实验目的:1.了解PN 结正向压降随温度变化的基本关系式。
2.在恒流供电条件下,测绘PN 结正向压降随温度变化曲线,并由此确定其灵敏度和被测PN 结材料的禁带宽度。
3.学习用PN 结测温的方法。
实验原理:理想PN 结的正向电流S I 和压降F V 存在如下近似关系)exp(kTqV I I FS F = (1) 其中q 为电子电荷;k 为波尔兹曼常数;T 为绝对温度;S I 为反向饱和电流,它是一个和PN 结材料的禁带宽度以及温度等有关的系数,可以证明])0(ex p[kTqV CT I g r S -= (2)其中C 是与结面积、掺质浓度等有关的常数;r 也是常数;)0(g V 为绝对零度时PN 结材料的导带底和价带顶的电势差。
将(2)式代入(1)式,两边取对数可得11)0(n r F g F V V InT q kT T IcIn q k V V +=-⎪⎪⎭⎫ ⎝⎛-= (3) 其中()rn F g InT qKT V T IcIn q k V V -=⎪⎪⎭⎫ ⎝⎛-=11)0(这就是PN 结正向压降作为电流和温度函数的表达式,它是PN 结温度传感器的基本方程。
令=F I 常数,则正向压降只随温度而变化,但是在方程(3)中,除线性项1V 外还包含非线性项1n V 项所引起的线性误差。
设温度由1T 变为T 时,正向电压由1F V 变为F V ,由(3)式可得[]rF g g F T T Ln q kT T T V V V V ⎪⎪⎭⎫⎝⎛---=111)0()0( (4) 按理想的线性温度影响,F V 应取如下形式:)(111T T TV V V F F F -∂∂+=理想 (5)TV F ∂∂1等于1T 温度时的T V F ∂∂值。
由(3)式可得r qk T V V T V F g F ---=∂∂111)0( (6) 所以()[]()rT T q kT T V V V T T r q k T V V V V F g g F g F 1111111)0()0(----=-⎥⎦⎤⎢⎣⎡---+=理想(7) 由理想线性温度响应(7)式和实际响应(4)式相比较,可得实际响应对线性的理论偏差为()r F T TLn q kT T T r q k V V )(11+--=-=∆理想 (8)设K T 3001=,K T 310=,取4.3=r ,由(8)式可得mV 048.0=∆,而相应的F V 的改变量约mV 20,相比之下误差甚小。
大学物理实验报告 PN结的温度特性的研究及应用得分教师签名批改日期深圳大学实验报告课程名称: 大学物理实验(三)实验名称: pn结的温度特性的研究及应用学院:组号指导教师:报告人: 学号: 班级:实验地点实验时间:实验报告提交时间:1一、实验设计方案1、实验目的了解PN结正向压降随温度变化的基本关系式。
在工作电流恒定的情况下,测绘PN结正向压降随温度变化曲线,并由此确定其灵敏度和被测PN结材料的禁带宽度。
设计用PN结测温的方法。
2、实验原理2.1 、PN结正向压降和工作电流、及所处的温度的关系:PN 结正向压降和工作电流、及所处的温度的基本函数关系如下:,,KcKT, ----------(1) 0lnlnVVTTVV,,,,,,,,,,,FgLNLqIqF,,其中: 导带,19q,,1.610C,为电子的电荷。
禁带EeV,gF-23-1,K=1.38×10JK,为玻尔兹曼常数,价带T――绝对温度。
图1 半导体的能带结I――PN结中正向电流。
f构γ 是热学中的比热容比,是常数。
V(0)是绝对零度时PN结材料的导带底和价带顶的电势差。
(半导体材料的能带理论中,把未g排满电子的能量区域称作价带,空着的能量区域叫导带,不能排列电子的能量区域叫禁带,如图1所示。
E叫禁带宽度.) g,,KTKc,,lnVT 其中,是线性项。
是非线性相。
0lnVVT,,,,,,NL,,LgqqIF,,非线性项较小,(常温下)可忽略其影响,在恒流供电条件下PN结的V对T的依赖关系F取决线性项,即正向压降几乎随温度升高而线性下降。
2.2、PN结测温的方法如果PN结正向压降在某一温度区域和温度变化恒定电流I F成线性关系,就可以利用这一特性将它作为温度传感器的转换探头,原理如图2所示。
将PN结做成的温度探头放在待温度显示结电压V F测环境中,通以恒定电流,温度变化可以引起结电压变化,图2 PN结测温原理测量结电压,将它转换成温度显示,从而达到测量温度的目的。