或门的真值表和逻辑表达式剖析

一、概述逻辑门是数字电子电路中重要的组成部分，其中与非门、或非门、异或门是其中的几种类型。

它们在数字电路中起到了至关重要的作用，并且在计算机科学和工程领域有着广泛的应用。

本文将对这几种逻辑门的逻辑表达式进行详细的介绍和分析。

二、与非门(AND非门)1. 与非门的逻辑表达式与非门是由一个与门和一个反相器组成的逻辑门，其输出与输入相反。

与非门的逻辑表达式可以表示为：输出= ~(A ∧ B)，其中∧表示与操作符，~表示反相操作符。

2. 与非门的功能与非门的主要功能是输出与输入相反的逻辑结果。

当输入的A和B同时为1时，输出为0；否则输出为1。

与非门常用于数字电路中的多种逻辑功能的实现，如加法器、乘法器等。

三、或非门(OR非门)1. 或非门的逻辑表达式或非门是由一个或门和一个反相器组成的逻辑门，其输出与输入相反。

或非门的逻辑表达式可以表示为：输出= ~(A ∨ B)，其中∨表示或操作符，~表示反相操作符。

2. 或非门的功能或非门的主要功能是输出与输入相反的逻辑结果。

当输入的A和B任意一个为1时，输出为0；否则输出为1。

或非门在数字电路中常用于多种逻辑功能的实现，如单片机的输入端口、输出端口等。

四、异或门(XOR门)1. 异或门的逻辑表达式异或门是一种常用的逻辑门，其逻辑表达式可以表示为：输出= A ⊕ B，其中⊕表示异或操作符。

2. 异或门的功能异或门的主要功能是实现两个输入信号的异或运算。

当输入的A和B 不相输出为1；否则输出为0。

异或门在数字电路中有着广泛的应用，如在加法器、校验电路、数据传输等领域。

五、总结在数字电子电路中，与非门、或非门、异或门是常用的逻辑门类型，它们分别实现了与、或、异或等不同的逻辑运算。

逻辑门的逻辑表达式对于理解和设计数字电路具有重要意义，通过对逻辑门的逻辑表达式的分析和理解，可以更好地应用和设计数字电路，提高数字电路的性能和可靠性。

希望本文对读者对于与非门、或非门、异或门的逻辑表达式有所帮助。

通常，把反映“条件”和“结果”之间的关系称为逻辑关系。

如果以电路的输入信号反映“条件”，以输出信号反映“结果”，此时电路输入、输出之间也就存在确定的逻辑关系。

数字电路就是实现特定逻辑关系的电路，因此，又称为逻辑电路。

逻辑电路的基本单元是逻辑门，它们反映了基本的逻辑关系。

基本逻辑关系和逻辑门2.1.1 基本逻辑关系和逻辑门逻辑电路中用到的基本逻辑关系有与逻辑、或逻辑和非逻辑，相应的逻辑门为与门、或门及非门。

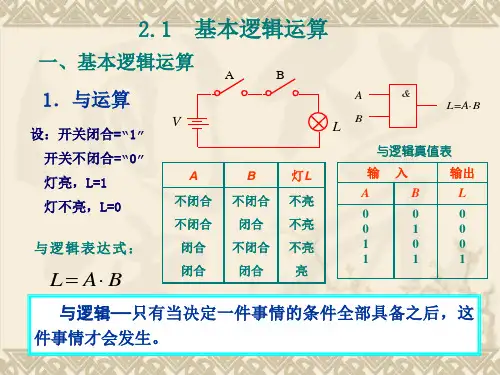
一、与逻辑及与门与逻辑指的是：只有当决定某一事件的全部条件都具备之后，该事件才发生，否则就不发生的一种因果关系。

如图2.1.1所示电路，只有当开关A 与B 全部闭合时，灯泡Y 才亮；若开关A 或B 其中有一个不闭合，灯泡Ｙ就不亮。

这种因果关系就是与逻辑关系，可表示为Y ＝AB ，读作“A 与B”。

在逻辑运算中，与逻辑称为逻辑乘。

与门是指能够实现与逻辑关系的门电路。

与门具有两个或多个输入端，一个输出端。

其逻辑符号如图2.1.2所示，为简便计，输入端只用A 和B 两个变量来表示。

与门的输出和输入之间的逻辑关系用逻辑表达式表示为：Y ＝AB ＝AB两输入端与门的真值表如表2.1.1所示。

波形图如图所示。

由此可见，与门的逻辑功能是，输入全部为高电平时，输出才是高电平，否则为低电平。

二、或逻辑及或门或逻辑指的是：在决定某事件的诸条件中，只要有一个或一个以上的条件具备，该事件就会发生；当所有条件都不具备时，该事件才不发生的一种因果关系。

如图2.1.4所示电路，只要开关A 或B 其中任一个闭合，灯泡Y 就亮；A 、B 都不闭合，灯泡Y 才不亮。

这种因果关系就是或逻辑关系。

可表示为：Y ＝A ＋B读作“A 或B”。

在逻辑运算中或逻辑称为逻辑加。

或门是指能够实现或逻辑关系的门电路。

或门具有两个或多个输入端，一个输出端。

其逻辑符号如图2.1.5所示。

表2.1.1 与门真值表图2.1.3 与门的波形图图2.1.4 或逻辑举例或门的输出与输入之间的逻辑关系用逻辑表达式表示为：Y＝A＋B两输入端或门电路的真值表和波形图分别如表2.1.2和图所示。

三输入异或门真值表计算详解
异或门的应用范围广，在实际应用中可以用来实现奇偶发生器或模2加法器，还可以用作加法器、异或密码、异或校检、异或门倍频器、可控反相器等等。

虽然异或不是开关代数的基本运算之一，但是在实际运用中我们依然会相当普遍地使用到分立的异或门。

因此，我们为了熟练了解、掌握异或门这一基本逻辑电路，对异或门电路进行了这次课程设计。

异或门的逻辑表达式：
Y=ABC+ABC+ABC+ABC=A⊕B⊕C
进一步可得到一位比较器的真值表：
异或逻辑运算（半加运算）
异或运算通常用符号♁表示，其运算规则为：。

与或非异或运算的逻辑表达式1.引言1.1 概述逻辑运算是计算机科学中非常重要的一部分，它在描述和处理真值（True/False）以及逻辑关系时起着至关重要的作用。

在逻辑运算中，与（AND）、或（OR）、非（NOT）以及异或（XOR）是我们经常会使用的四种基本逻辑运算。

与运算是指当且仅当所有的输入条件都为真时，结果才为真。

它的逻辑表达式可以用逻辑符号“∧”表示，例如，表达式“A∧B”代表A和B 都为真时，结果为真。

与运算除了在逻辑中常用外，在计算机科学中也广泛应用，例如在编程语言中，我们常常使用与运算来判断两个条件是否同时满足。

或运算是指当且仅当至少有一个输入条件为真时，结果才为真。

它的逻辑表达式可以用逻辑符号“∨”表示，例如，表达式“A∨B”代表A或者B其中一个为真时，结果为真。

或运算在逻辑中的一个重要应用是进行多个条件的判断，只要其中一个条件成立，我们就可以进行相应的操作。

非运算是指将输入条件取反，即如果原始条件为真，则取反后为假；如果原始条件为假，则取反后为真。

它的逻辑表达式可以用逻辑符号“¬”表示，例如，表达式“¬A”代表A的逆否命题。

非运算常常用于取反判断、条件判断等场景中，是逻辑推理中的一种重要手段。

异或运算是指当且仅当两个输入条件不同时，结果才为真。

它的逻辑表达式可以用逻辑符号“⊕”表示，例如，表达式“A⊕B”代表A和B不同时，结果为真。

异或运算在计算机领域特别常用，经常应用于数据的加密与解密、错误检测等方面。

本文将详细探讨与、或、非以及异或运算的定义、特点和逻辑表达式，并对它们的真值表进行分析。

同时，我们还将讨论逻辑运算在实际应用中的一些例子，帮助读者更好地理解逻辑运算的重要性和应用场景。

在深入理解这些逻辑运算的基础上，我们可以更准确地进行问题的分析和解决。

文章结构部分的内容如下:1.2 文章结构本文主要围绕与运算、或运算、非运算和异或运算的逻辑表达式展开讨论。

序在现代电子学和计算机科学中，逻辑门电路是至关重要的基础组成部分。

而逻辑门电路最基本的形式就是7种逻辑门，它们分别是与门、或门、非门、异或门、与非门、或非门以及同或门。

每种逻辑门都有其独特的逻辑符号和逻辑表达式，它们在数字电子电路中扮演着不可或缺的角色。

接下来，我们将深入探讨这7种逻辑门电路的逻辑符号和逻辑表达式，并从浅到深逐步分析它们的原理和应用。

一、与门与门是最简单的逻辑门之一，它的逻辑符号是一个“Λ”形状，而其逻辑表达式可以用“Y=A·B”来表示。

在与门电路中，只有当输入的布尔值均为1时，输出才会为1；否则输出为0。

这个逻辑表达式实际上就表明了与门的原理，即只有当所有输入为真时，输出才为真。

二、或门或门的逻辑符号是一个“V”形状，而其逻辑表达式可以用“Y=A+B”来表示。

与与门相反，或门只要有一个输入为1，输出就为1；只有当所有输入为0时，输出才为0。

可以看出，或门的逻辑表达式和与门的逻辑表达式是相对应的。

三、非门非门的逻辑符号是一个“￢”形状，而其逻辑表达式可以用“Y=￢A”来表示。

非门的原理是将输入的布尔值取反，即如果输入为1，则输出为0；如果输入为0，则输出为1。

四、异或门异或门的逻辑符号是一个带有一个加号的“⊕”形状，而其逻辑表达式可以用“Y=A⊕B”来表示。

异或门的原理是只有当输入不同时为1时，输出为1；否则输出为0。

异或门也常被用于比较两个输入是否相等的情况。

五、与非门与非门实际上是与门和非门的组合，其逻辑符号是一个与门后加上一个小圆点的符号，而其逻辑表达式可以用“Y=￢(A·B)”表示。

与非门的原理是先进行与运算，再对结果取反。

六、或非门或非门实际上是或门和非门的组合，其逻辑符号是一个或门后加上一个小圆点的符号，而其逻辑表达式可以用“Y=￢(A+B)”表示。

或非门的原理是先进行或运算，再对结果取反。

七、同或门同或门的逻辑符号是一个带有一个加号和一个横线的“⊙”形状，而其逻辑表达式可以用“Y=￢(A⊕B)”表示。

一、引言输入与逻辑是电子电路设计中的重要内容，利用其可以实现各种逻辑功能，从而构建数字电路。

在输入与逻辑中，真值表和表达式是常用的描述和分析工具。

本文将介绍输入与逻辑的真值表和表达式的概念、应用和相关知识。

二、输入与逻辑的基本概念1. 输入与逻辑概述输入与逻辑是数字电路中最基本的运算方式，通过输入与逻辑可以实现逻辑运算，比如与、或、非等运算。

输入与逻辑常用于逻辑门、寄存器、计数器等电路的设计和实现。

2. 真值表真值表是描述输入与逻辑运算结果的一种方法，它列出了输入变量和对应的逻辑输出结果。

真值表可以直观地展现输入与逻辑的运算规则和结果。

3. 逻辑表达式逻辑表达式是使用逻辑运算符和变量表示逻辑函数的一种方式。

逻辑表达式可以方便地描述输入与逻辑的功能和运算规则，是在电路设计中常用的描述方式。

三、输入与逻辑的真值表1. 真值表的基本结构真值表包括输入变量和对应的逻辑输出结果，可以使用真值表来描述逻辑函数的运算规则和输入输出关系。

2. 真值表的应用真值表可以帮助工程师分析输入与逻辑的功能、性能和运算规则，也可以用于逻辑函数的简化和优化。

3. 真值表的编制方法编制真值表时，需要确定输入变量的取值范围，列出所有可能的输入组合，并计算对应的输出结果。

真值表应该包含所有可能的输入组合，以全面地描述逻辑函数的运算规则。

四、输入与逻辑的逻辑表达式1. 逻辑表达式的基本形式逻辑表达式由输入变量和逻辑运算符组成，可以使用逻辑表达式来描述逻辑函数的运算规则和输入输出关系。

2. 逻辑表达式的应用逻辑表达式可以方便地描述和分析输入与逻辑的功能、结构和运算规则，也可以用于电路设计中的数字信号处理和逻辑分析。

3. 逻辑表达式的化简化简逻辑表达式可以减少电路的复杂度和功耗，提高电路的性能和可靠性。

化简逻辑表达式的方法包括卡诺图法、毕尔定理等。

五、输入与逻辑的应用举例1. 逻辑门电路逻辑门电路是输入与逻辑的重要应用之一，常用的逻辑门包括与门、或门、非门等。

各种逻辑门的符号及表达式
在数字电路中，逻辑门是最基本的电子元件之一。

它们是用于实现逻辑功能的电路。

逻辑门根据它们执行的逻辑操作的不同而被分类为不同的类型：与门、或门、非门、异或门等。

以下是各种逻辑门的符号和表达式：
1.与门：符号为“∧”，表达式为Y=A∧B。

与门只有当输入A和输入B均为1时输出1，否则输出0。

2.或门：符号为“∨”，表达式为Y=A∨B。

或门只有当输入A或输入B至少有一个为1时输出1，否则输出0。

3.非门：符号为“”，表达式为Y=A。

非门的输出与输入相反，即输入为0时输出1，输入为1时输出0。

4.异或门：符号为“⊕”，表达式为Y=A⊕B。

异或门只有当输入A和输入B不同时输出1，否则输出0。

以上是常见的逻辑门符号和表达式，它们的组合可以构建出各种复杂的数字电路，实现各种逻辑功能。

- 1 -。

第6次课三种基本逻辑关系、分立元件门电路、复合逻辑门电路●本次重点内容：1、与、或、非三种基本逻辑关系及真值表、逻辑表达式、门电路逻辑符号。

2、分立元件门电路的工作原理。

3、复合逻辑关系：与非、或非、与或非、异或、同或的真值表、逻辑表达式、门电路逻辑符号。

●教学过程6.1三种基本逻辑关系一、与逻辑关系所谓与逻辑关系：就是指决定某事件结果的所有条件全部具备，结果才能发生，而只要其中一个条件不具备，结果就不能发生，这种逻辑关系称为与逻辑关系。

与逻辑示意如图6-1所示：用A，B表示条件，即开关的状态；用Y表示结果，即表示灯的亮、灭状态。

图6-1 与逻辑示意图开关：“1”表示开关闭合，“0”表示开关断开。

灯：“1”表示灯亮，“0”表示灯灭。

根据所有可能的开关组合状态与灯亮、灭的对应关系，可以列出真值表。

如表6-1所示。

表6-1 与逻辑真值表由表6-1可以得出“与”逻辑关系为“有0出0，全1出1”。

与门是实现与逻辑关系的电路，其逻辑符号如图6-2所示：图6-2 与逻辑符号二、或逻辑—在A，B等多个条件中，只要具备其中一个条件，事件就会发生；只有所有条件均不具备时，事件才不会发生，这种因果关系称为或逻辑关系。

或逻辑示意如图6-3所示：图6-3 或逻辑示意图经分析开关A，B的闭合情况，可以列出或逻辑真值表如表6-2所示：表6-2 或逻辑真值表由上表6-2可以得知或逻辑功能为“有1出1，全0出0”。

或门是实现或逻辑关系的电路，其逻辑符号如图6-4所示。

图6-4或逻辑符号三、非逻辑：决定事件结果只有一个条件，当条件具备时，结果就不发生；当条件不具备时，结果就发生。

这种因果关系称为非逻辑关系。

非逻辑示意如图6-5所示。

当开关A闭合时，灯Y灭；当开关A断开时，灯Y亮。

可见，对灯亮来说，开关A闭合是非逻辑关系。

图6-5非逻辑示意如图经分析可以列出或逻辑真值表6-3。

表6-3 非逻辑真值表由上表可以得知非逻辑功能为“是0出1，是1出0”。