5逻辑电路图、真值表和逻辑函数式转换

逻辑函数及其表示方法(案例分析)表示一个逻辑函数有多种方法，常用的有：真值表、逻辑函数式、逻辑图等3种。

它们各有特点，有相互联系，还可以相互转换，现介绍如下：1.真值表 真值表时根据给定的逻辑问题，把输入逻辑变量各种可能取值的组合和对应的输出函数值排列成的表格。

它表示了逻辑函数与逻辑变量各种取值之间的一一对应关系。

逻辑函数的真值表具有唯一性。

若两个逻辑函数具有相同的真值表，则两个逻辑函数必然相等。

当逻辑函数有n 个变量时，共有2n 个不同变量取值组合。

在列真值表时，为避免遗漏，变脸取值的组合一般按n 位自然二进制数递增顺序列出。

用真值表表示逻辑函数的优点是直观、明了，可直接看成逻辑函数值和变量取值的关系。

例： 试列出逻辑函数B A AB Y +=的真值表。

解：该逻辑函数有2个输入变量，就有22=4种取值。

把输入变量A 、B 的每种取值情况分别代入B A AB Y +=中，进行逻辑运算，求出逻辑函数值，列入表中，就得到Y 的真值表。

表 1 Y=AB+AB 的真值表2.逻辑函数式 逻辑函数式时用与、或、非等 逻辑运算来表示输入变量和输出函数间因果关系的逻辑函数式。

由真值表直接写出的逻辑式是标准的与-或表达式。

写标准与-或表达式的方法是：(1)把任意一组变量取值中的1代以原变量，0代以反变量，由此得到一组变量的与组合，如A 、B 、C 三个变量的取值为001，则代换后得到变量与组合为C B A 。

(2)把逻辑函数值为1所对应的各变量的与组合进行逻辑加，便得到标准的与-或逻辑式。

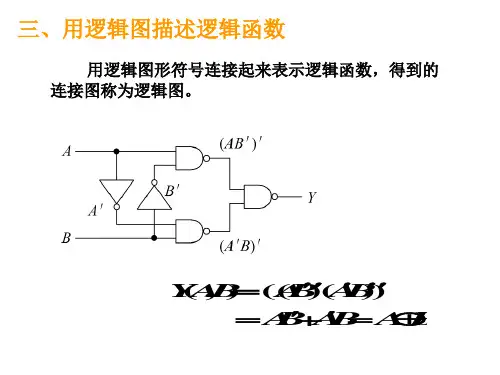
3.逻辑图逻辑图是用基本逻辑门和符合逻辑门的逻辑符号组成的对应于某一逻辑功能的电路图。

根据逻辑函数式画逻辑图时，只要把逻辑函数式中各逻辑运算用对应门电路的逻辑符号代替，可以画出和逻辑函数对应的逻辑图。

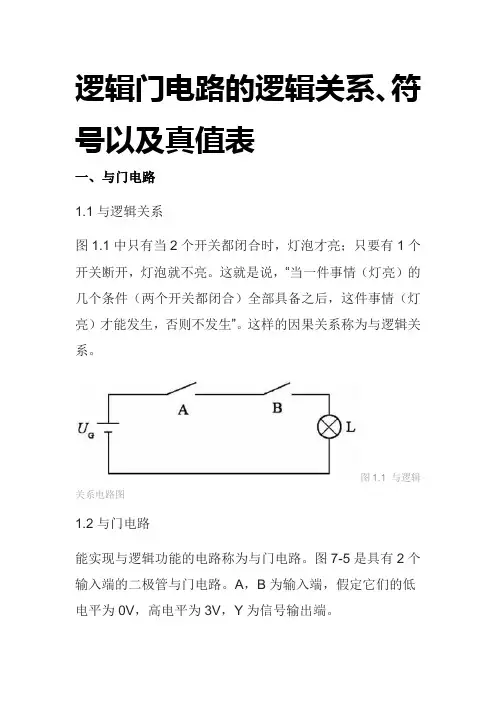
逻辑门电路的逻辑关系、符号以及真值表一、与门电路1.1与逻辑关系图1.1中只有当2个开关都闭合时，灯泡才亮；只要有1个开关断开，灯泡就不亮。

这就是说，“当一件事情（灯亮）的几个条件（两个开关都闭合）全部具备之后，这件事情（灯亮）才能发生，否则不发生”。

这样的因果关系称为与逻辑关系。

图1.1 与逻辑关系电路图1.2与门电路能实现与逻辑功能的电路称为与门电路。

图7-5是具有2个输入端的二极管与门电路。

A，B为输入端，假定它们的低电平为0V，高电平为3V，Y为信号输出端。

图1.2与门电路(1) 当A，B都处于低电平0V时，二极管VD1，VD2同时导通，Y=0V，输出低电平。

（忽略二极管的正向压降，下同）。

(2) 当A=0V，B=3V时，VD1优先导通，Y被箝位在0V，VD2反偏而截止。

(3) 当A=3V，B=0V时，VD2优先导通，Y被箝位在0V，VD1反偏而截止。

(4) 当A，B都处在高电平3V时，VD1与VD2均截止，Y 端输出高电平（即3V）。

与逻辑关系的逻辑函数表达式为Y=A*B。

表1.1是与门真值表，从真值表可以看出，与门电路的逻辑功能是“有0出0，全1出1”。

与门的逻辑符号如图1.3所示。

表1.1 与门真值表图1.3与门的逻辑符二、或门电路2.1或逻辑关系图2.1中电路由2个开关和灯泡组成。

由图可知，在决定一件事情的各种条件中，至少具备一个条件，这件事情就会发生，这种因果关系称为或逻辑关系。

图2.1 或逻辑关系电路图2.2或门电路能实现或逻辑关系的电路称为或门电路。

图2.2所示为具有2个输入端的二极管或门电路。

图2.2 或门电路真值表见表2.1，从真值表可以看出，或门的逻辑功能为“有1出1，全0出0”。

或门的逻辑符号如图2.3所示。

表2.1 或门真值表图2.3 或门逻辑符号三、非门电路（反相器）3.1非逻辑关系如图3.1开关与灯泡并联，当开关断开时，灯亮；开关闭合时，灯不亮。

这就是说，“事情（灯亮）和条件（开关）总是呈相反状态”，这种关系称为非逻辑关系。

根据真值表写出逻辑函数式在逻辑学和计算机科学领域中，逻辑函数式是一个重要的概念。

它是二进制逻辑电路设计的基础，通常用来描述逻辑函数的行为。

在这篇文档中，我们将探讨如何根据真值表来写出逻辑函数式。

我们将介绍真值表的概念、逻辑函数的基础知识以及如何从真值表中获得逻辑函数式。

什么是真值表？真值表是逻辑函数行为的一种表示形式，它通过列出函数的输入和输出来展示函数的行为。

真值表中的每行都描述了一个函数输入的组合和相应的输出值。

对于输入变量的每种组合，真值表都给出了这个函数的输出结果。

例如，下面是一个真值表的例子：| A | B | C | F | | - | - | - | - | | 0 | 0 | 0 | 1 | | 0 | 0 | 1 | 0 | | 0 | 1 | 0 | 1 | | 0 | 1 | 1 | 0 | | 1 | 0 | 0 | 0 | | 1 | 0 | 1 | 1 | | 1 | 1 | 0 | 0 | | 1 | 1 | 1 | 1 |在这张真值表中，A、B、C是输入变量，F是输出变量。

每一行都代表了一个输入变量的组合和相应的输出值。

例如，第一行(0,0,0,1)描述当A、B和C都为0时，F 的值为1。

逻辑函数基础知识逻辑函数是指在二进制逻辑中常常使用的一种函数，其输出值只有0和1两种可能。

例如，A AND B就是一个逻辑函数，它可以描述当A和B都为1时，输出1；否则输出0。

在逻辑函数中，输入变量的个数被称为“参数个数”，参数的数量用n表示，这些参数被表示成变量x1，x2，x3，......，xn。

在逻辑函数中，每一个函数的状态都有一个二进制编码或"真值"来表示，因此逻辑函数可以用一个真值表来描述。

对于n个二进制变量的所有可能的输入组合，逻辑函数只有两个可能的输出值，0或1。

因此，如果我们将这些变量的输入组合数分为2的n次幂个，就可以描述所有可能的输入组合，并将它们对应到0和1中的一个值，这些对应就构成了一个真值表。