第六讲 真值表与基本逻辑运算
- 格式:ppt
- 大小:1.49 MB
- 文档页数:29


真值表什么是真值表真值表是逻辑学中用来描述逻辑命题或者布尔代数的一个工具,它列举了每个可能输入的所有输出结果。
真值表在逻辑电路设计、计算机科学和数学领域有着广泛的应用。
真值表的表示方法真值表的表示方法是使用表格展示逻辑命题的所有可能的输入和对应的输出结果。
通常,真值表的第一行是列标题,用来代表输入变量的名称;第一列是行标题,用来代表输入的各种可能情况;剩下的部分则是输出结果。
例如,一个简单的真值表如下所示:输入1 输入2 输出0 0 00 1 01 0 11 1 1在这个示例中,输入1和输入2是逻辑命题的两个输入变量,输出则代表根据输入变量的不同组合所对应的输出结果。
真值表的应用逻辑电路设计在逻辑电路设计中,真值表用于描述逻辑门的功能和行为。
逻辑门通常有与门(AND)、或门(OR)、非门(NOT)等,它们根据输入变量的情况输出特定的结果。
通过使用真值表,我们可以清楚地了解逻辑门的输入和输出之间的关系,从而更好地设计和优化逻辑电路。
布尔代数布尔代数是一种逻辑代数,它利用真值表来进行逻辑推理和运算。
在布尔代数中,使用不同的逻辑运算符如与、或、非等来组合和操作逻辑命题。
真值表能够帮助我们理解逻辑运算符的运算规则,并通过推理和转化,解决复杂的逻辑问题。
计算机科学真值表在计算机科学中也有着重要的应用。
比如,在编写程序时,使用逻辑运算符进行条件判断和逻辑操作是非常常见的。
在这种情况下,真值表可以帮助程序员理解不同的逻辑条件下程序的行为,并更好地进行程序设计和调试。
如何生成真值表生成真值表的方法很简单。
首先,根据逻辑命题的输入变量数量确定表格的列数,然后列出所有可能的输入情况,每种情况占据一行。
接下来,根据逻辑命题的逻辑运算规则,计算出每种输入情况下的输出结果,填写到对应的行和列中。
例如,对于一个有两个输入变量的逻辑命题而言,就需要列出4种可能的输入情况(每个变量有两种取值),然后根据逻辑运算规则计算出对应的输出结果,填写到真值表中。

逻辑符号及真值表
这些逻辑符号可以用于构建命题逻辑中复杂命题的逻辑结构,从而方便我们进行推理和论证。
在使用逻辑符号时,通常会用到真值表来验证命题的逻辑结构。
真值表是一种用来列出命题不同取值组合的表格。
在真值表中,每一行代表一种取值组合,每一列代表一个命题变量或逻辑符号。
通过对每个命题变量进行相应的逻辑运算,可以得出最终命题的真值(T 或F)。
例如,在合取命题p ∧ q中,p和q为命题变量,∧为逻辑符号。
我们可以列出如下的真值表:
p | q | p ∧ q
--|---|------
T | T | T
T | F | F
F | T | F
F | F | F
从表中可以看出,在p为真、q为真的情况下,p ∧ q的真值为真(T)。
而在其他情况下,其真值为假(F)。
通过使用逻辑符号和真值表,我们可以更加清晰地理解和分析命题逻辑中的复杂结构,从而更加准确地进行推理和论证。
- 1 -。

半加器真值表和逻辑表达式一、半加器真值表和逻辑表达式的基础知识半加器可是数字电路里超有趣的小玩意儿呢!那什么是半加器呢?简单说呀,它就是一种只考虑两个一位二进制数相加,不考虑低位进位的电路。
1. 真值表我们先来说说真值表。
真值表就是把输入和输出的所有可能情况都列出来。
对于半加器来说,它有两个输入,分别设为A和B,还有两个输出,一个是和(S),一个是进位(C)。
当A = 0,B = 0的时候呢,S = 0,C = 0。
就像你有0个苹果,再加上0个苹果,总共还是0个苹果,也没有多余的能进位。
当A = 0,B = 1的时候,S = 1,C = 0。
这就好比你本来没有苹果,别人给你1个,那你就有1个苹果了,还没有到能进位的程度。
当A = 1,B = 0的时候,S = 1,C = 0。
和上面的情况类似,只是换了一下谁有苹果谁没有。
当A = 1,B = 1的时候,S = 0,C = 1。
这个时候呢,1加1等于2了,在二进制里就是10,所以和是0,进位是1。
2. 逻辑表达式那怎么用数学式子来表示半加器呢?对于和(S)的逻辑表达式是S=A⊕B,这个⊕符号表示异或运算哦。
异或运算就是两个输入不同的时候输出为1,相同的时候输出为0。
就像A和B一个是0一个是1或者一个是1一个是0的时候,S就是1啦。
对于进位(C)的逻辑表达式就简单啦,C = A·B,这个·表示与运算。
就是A和B都为1的时候,C才是1,就像只有你和小伙伴都有苹果的时候,才会有多余的能进位。
二、半加器的实际应用半加器虽然看起来简单,但是它可是构建更复杂数字电路的基础呢。
1. 在加法器中的应用全加器就会用到半加器的原理。
全加器是考虑低位进位的加法器,它可以由两个半加器和一些逻辑门组合而成。
想象一下,我们要计算多位二进制数的加法,就像搭积木一样,半加器就是那些基础的小积木块,把它们组合起来就能完成更复杂的计算啦。
2. 在其他数字电路中的应用在计数器、寄存器等数字电路组件中,半加器的逻辑也可能会被用到。

联言判断
包含两个联言支的联言判断,其逻辑形式可表示为:p并且q,合取式为:p∧q
联言判断的真假(真值表)
选言判断
1、相容选言判断
逻辑形式:p或者q,p∨q
真假表表明:p∨q假,当且仅当p和q同假。
2、不相容选言判断
逻辑形式:要么p,要么q, p∨q
真值表表明:p∨q假,当且仅当p和q同真或同假。
假言判断
充分条件假言判断
1、充分条件假言判断:
真假表表明:p →q为假,当且仅当p真而q假。
2、必要条件假言判断:
真值表表明:p ←q为假,当且仅当p假而q真
3、充分必要条件假言判断
真值表表明:p q 真,当且仅当p 和q 同真或同假。
p q p q
T T T
T F F
F T F
F F T
负判断
逻辑形式:并非p ,逻辑符号表示:“
”或者“ ”
T F
F T
•
p p p。
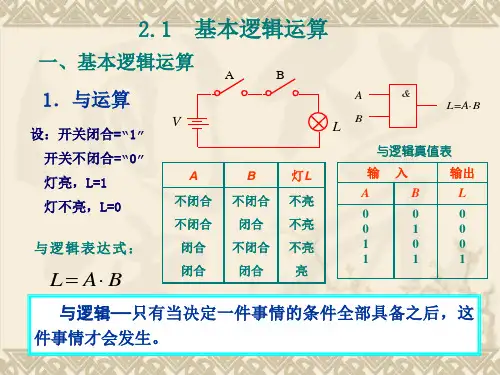
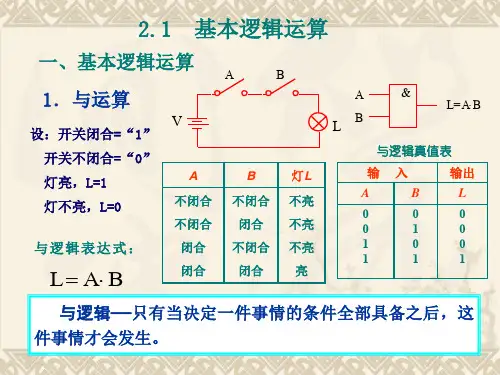



真值表用法一、真值表是什么呢?真值表就像是一个超级有用的小工具,用来表示逻辑关系的。
比如说,在逻辑运算里,像与、或、非这些运算,真值表就能清楚地把各种输入情况下的输出结果都列出来。
就好像我们有一个小盒子,它有不同的入口(输入),然后根据里面的规则,会有对应的出口(输出),真值表就是把这些入口和出口的关系都明明白白地写出来啦。
二、真值表的基本组成部分1. 输入变量这些就像是我们刚刚说的小盒子的入口。
在逻辑运算里,可能有一个或者好几个输入变量呢。
比如说在一个简单的与运算里,可能有A和B两个输入变量。
每个输入变量都可以有两种状态,真(用1表示)或者假(用0表示)。
这就像我们开灯关灯一样,要么开(1),要么关(0)。
2. 输出结果这就是小盒子的出口啦。
根据输入变量的不同组合,按照逻辑运算的规则,就会得到相应的输出结果。
还拿与运算来说,如果A 是0,B是0,那么输出就是0;如果A是1,B是0,输出也是0;只有当A是1,B是1的时候,输出才是1。
三、真值表的用法1. 在逻辑推理中的用法在逻辑推理的时候,真值表可以帮助我们判断各种命题之间的关系。
比如说有两个命题P和Q,我们想知道它们之间是等价关系呢,还是蕴含关系之类的。
我们就可以把P和Q的各种可能取值(真或假)都列在真值表里,然后根据逻辑关系的定义,看对应的输出结果。
如果在所有可能的输入情况下,P和Q的输出结果都一样,那它们就是等价的。
就像两个人对同一件事情的看法,不管这件事情是什么情况,他们的观点总是一样的,那他们的看法就是等价的。
2. 在电路设计中的用法在电路设计里,真值表可太重要啦。
电路里的各种门电路,像与门、或门、非门之类的,它们的行为就可以用真值表来描述。
比如说我们要设计一个简单的报警电路,当两个条件都满足的时候(比如温度过高和烟雾浓度超标)才报警。
那我们就可以用与门来实现这个功能,通过真值表我们就能清楚地知道,什么时候这个与门会输出高电平(表示报警),什么时候输出低电平(表示正常)。
