初中数学如何证明圆的切线

初中数学什么是切线长定理
初中数学中，切线长定理是与圆相关的一个重要概念。

下面我将详细介绍切线长定理的定义、性质和相关概念。

1. 切线长定理的定义：
-切线长定理：在一个圆上，一个角的顶点在切点上，另外两个顶点在圆上，这个角的两条边分别与切线相交，那么这两条切线的长度相等。

2. 切线长定理的性质：
-定理性质1：切线长度相等。

如果一个圆上的两条切线与同一个角相交，且角的顶点在切点上，那么这两条切线的长度相等。

3. 切线长定理的相关概念：
-切点：切线与圆相交的点称为切点。

-切线长度：切线的长度即为从切点到圆心的距离。

切线长定理是初中数学中的一个重要概念，它可以帮助我们理解和应用几何知识，解决与切线和圆相关的问题。

在应用切线长定理时，需要注意定理的定义和性质，并运用几何知识进行推理和分析。

例如，如果我们需要判断两条切线的长度是否相等，我们可以先找到这两条切线与同一个角相交，并且角的顶点在切点上。

然后根据切线长定理的性质，我们可以得出这两条切线的长度相等。

希望以上内容能够满足你对切线长定理的了解。

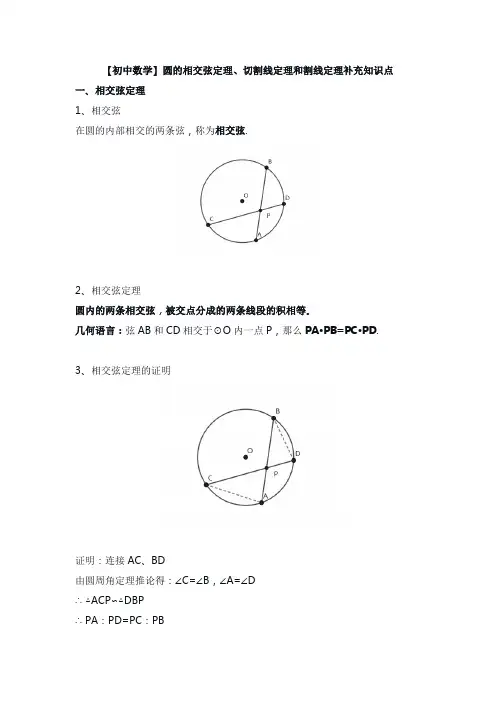
【初中数学】圆的相交弦定理、切割线定理和割线定理补充知识点一、相交弦定理1、相交弦在圆的内部相交的两条弦，称为相交弦.2、相交弦定理圆内的两条相交弦，被交点分成的两条线段的积相等。

几何语言：弦AB和CD相交于⊙O内一点P，那么PA·PB=PC·PD. 3、相交弦定理的证明证明：连接AC、BD由圆周角定理推论得：∠C=∠B，∠A=∠D∴△ACP∽△DBP∴ PA：PD=PC：PB二、切割线定理1、切割线定理从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。

几何语言：BC是⊙O的一条割线，PA是⊙O的一条切线，切点为A，则：PA²=PB·PC。

2、切割线定理的证明证明：如图，连接AB，AC∵ PA是圆O的切线，由弦切角定理可得∴∠PAC=∠B∵∠APB=∠CPA∴△APC∽△BPA∴ PA：BP=PC：PA三、割线定理1、割线定理从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等。

几何语言：从⊙O一点P引圆的两条割线AB、CD，则：PA·PB=PC·PD.2、割线定理证明证明：如图，连接AD、BC，由圆周角定理推论，得：∠D=∠B∵∠BPC=∠DPA∴△BPC∽△DPA∴ PB：PD=PC：PA∴ PA·PB=PC·PD四、例题例1、如图，在⊙O中，弦AB=CD，AB⊥CD于点E，已知CE·ED=3,BE =1，求⊙O的直径。

解：作OH⊥AB于H，OG⊥CD于G，连接OA由相交弦定理得：CE·ED=AE·EB∴ 3=AE×1∴ AE=3∴ AB=AE+EB=3+1=4∴ AB=CD=4∴ AH=HB=2∴ HE=HB-EB=2-1=1∵ AB=CD，AB⊥CD∴ OH=OG∴四边形OGEH为正方形∴ OH=HE=1由勾股定理得，OA=,∴⊙O的直径为,例2、如题图,⊙O的弦AB,CD相交于点E,过点A作圆O的切线与DC的延长线交于点P,若PA=6，AE=9，PC=3, CE:ED=2:1 ，求BE的值。

切线和割线知识定位切割线定理是初中平面几何中的重要定理,它应用广泛,各地的中考题有相当多的题目都用到它,竞赛题也不例外.且题目新颖，灵活多变，学生往往甚感困难。

因此有计划、有目的、有步骤地对切割线定理进行补充、演化无疑是十分有益的。

知识梳理知识梳理1：切割线定理切割线定理:从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。

是圆幂定理的之一。

几何语言:∵PT切⊙O于点T，PDC是⊙O的割线∴PT²=PD·PC(切割线定理)知识梳理2：割线定理从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等几何语言:∵PT是⊙O切线，PBA、PDC是⊙O的割线∴PD·PC=PA·PB(切割线定理推论)(割线定理)由上可知:PT²=PA·PB=PC·PD例题精讲【试题来源】【题目】如图，等边三角形ABC中，边AB与⊙O相切于点H，边BC,CA与⊙O交于点D,E,F,G。

已知AG=2,GF=6,FC=1.则DE=_______.【答案】21【解析】2由切割线定理可知16：4又AH AG AF,AHAC AG=•=∴==2又99故5则25又7，9，AC AG GF FCAB ACBHBD BE BHCE CD CF CG BC AC=++=∴===•==•=•===【知识点】切线和割线【适用场合】当堂例题【难度系数】3【试题来源】【题目】如图，⊙O和⊙O′都经过点A和B，PQ切⊙O于P，交⊙O′于Q，M，交AB的延长线于N.求证:2PN MN NQ=⋅.【答案】【解析】【知识点】切线和割线【适用场合】当堂例题【难度系数】3【试题来源】【题目】如图,已知点P是O外一点,PS,PT是O的两条切线，过点P作O的割线PAB,交O于A.B两点，并交ST于点C,求证:1111()2PC PA PB=+.【答案】【解析】【知识点】切线和割线【适用场合】当堂例题【难度系数】3【试题来源】【题目】如图，设△ABC是直角三角形，点D在斜边BC上，BD＝4DC。

用切线的性质牵线搭桥袁芝馨圆的切线是圆中一个非常重要的知识点，前面我们已经给同学们介绍了如何进行切线的判定，这一讲我们将给同学们介绍如何灵活运用切线的性质，为圆中有关的证明与计算牵线搭桥． 一、与切线有关的性质1．切线的性质定理：圆的切线垂直于过切点的半径． 2．切线的有关性质： （1）与圆只有一个交点；（2）圆心到切线的距离等于半径（d=r ）； （3）切线垂直于过切点的半径；（4）经过圆心垂直于切线的直线必过切点； （5）经过切点垂直于切线的直线必过圆心．【说明】：（4）、（5）只是由（3）推出的有关性质． 3．切线长定理从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角． 4．已知切线常考虑：（1）切线的性质（垂直于过切点的半径）；（2）切线长定理．5．已知切线常做的辅助线：作过切点的半径，构造直角三角形．二、例题讲解例1 如图1，AE 与⊙O 相切于点B ，AO 的延长线交⊙O 于点C ，连结BC ． 若∠A=36°，则∠CBE 的度数为_______．分析：连接OB （图2），则△ABO 为直角三角形，而△OBC 是等腰三角形，利用角之间的关系进行相互转换，便可求得∠CBE 的度数．解：连接OB （图2），∵ AE 为⊙O 的切线， ∴ ∠ABO=90°． 在Rt △ABO 中，∵∠A=36°， ∴∠AOB=54°． ∵ OB=OC ，∴∠C=∠OBC ， ∴ ∠AOB=∠OBC +∠C=2∠C ． ∴∠C=27°．∴∠CBE=∠A+∠C=63°．思考：若将∠A=36° 换成∠A =α ，那么∠CBE 的度数是多少？（答案：︒+452α）COBECOABE例2 如图1，AB 为⊙O 的直径，PQ 切⊙O 于点T ，AC ⊥PQ 于点C ，交⊙O 于点D ． （1）求证：AT平分∠BAC ；（2）若AD=2，TC=3，求⊙O 半径的长．【分析】（1）连结OT （图2），因为PQ 是⊙O 的切线，利用切线的性质，再进行角之间的相互转换，便可以得出结论；（2）过点O 作OM ⊥AC （图3），由垂径定理和勾股定理可以求出⊙O 半径的长． （1）证明：连结OT （图2）， ∵ PQ 是⊙O 的切线，∴ OT ⊥PQ ．∵ AC ⊥PQ ，∴ AC ∥OT ．∴∠OTA=∠TAC ． ∵ OA=OT ，∴∠OTA=∠OAT ． ∴∠OA T=∠CAT ．即AT 平分∠BAC ． （2）解：过点O 作OM ⊥AC （图3）， ∴ AM=MD =21AD=1 ． 又 ∠OTC=∠ACT=∠OMC =90° ∴ 四边形OTCM 是矩形． ∴ OM=TC=3．在Rt △AMO 中， ∵ OA 2=OM 2+AM 2=()23+12= 4，∴ OA=2．即⊙O 半径的长为2．说明：灵活运用圆的有关知识是解题的关键．思考：若连结BD 交OT 于点E （如图4），也可以求出⊙O 半径的长，请同学们课下完成．例3 已知：如图1，BAP 是⊙O 的割线，AB 是⊙O 的直径，PC 是⊙O 的切线，C 为切点，BD ⊥PC 于点D ，交⊙O 于点E ，且PA=AO=1．（1）求∠P 的度数； （2）求DE 的长．分析：由AB 是⊙O 的直径，PC 是⊙O 的切线，故连结OC 、AE 后（图2），可得∠PCO =∠AEB = 90°．利用直角三角形的有关知识，可求得∠P 的度数和DE 的长．解：（1）连结OC （图2），∵ PC 是⊙O 的切线，∴∠PCO = 90°． 在Rt △OCP 中，∵ PA=AO=OC ，图1 AB D O例2图1例2图2例2图3例2图4∴ OC=21PO ．∴∠P=30°． （2）在Rt △BDP 中，∵ PB=AP+AO+BO=3，∠P=30°， ∴ BD=21PB=23． 连接AE ，∵ AB 是⊙O 的直径，∴ ∠AEB =90°． ∴ ∠AEB=∠D = 90°．∴ AE ∥PD ． ∴ ∠EAB =∠P =30°．∴ BE=21AB=1． ∴ DE=DB －BE=21． 答：∠P=30°，DE=21． 说明：已知切线通常作过切点的半径，已知直径通常构造直径所对的圆周角．例4 如图1，AD 是半圆O 的直径，AB 、CD 与半圆O 切于点A 、D ，BC 切半圆O 于点E ，如果AB=4，CD=9，求半圆O 的直径．分析：由于BC 、CD 是由半圆O 外的一点C 向圆所作的两条切线上的线段，即切线长（切线AB 与BC 同理），因此可以利用切线长定理求出直径的长．解：过点B 作BF ⊥CD 于F ，如图2，∵ BA 是半圆O 的切线，AD 是半圆O 的直径， ∴ BA ⊥AD ． 同理CD ⊥AD ， ∴ 四边形ABFD 是矩形．∴ BF=AD ，FD=BA=4． ∴ CF=CD -CF=5． ∵ CB 、BA 和CD 都是半圆O 的切线， ∴ CE=CD=9，BE=BA=4． ∴ CB=CE+EB=13． 在Rt △CFB 中，∵ 22CF CB BF -==12． ∴ AD=12．即半⊙O 直径的长为12．说明：（1）由于AB 、CD 、BC 都是半圆O 的切线，在有关圆的切线计算问题中，我们可联想切线长定理；（2）直角梯形常用的辅助线是做它的高线．图1。

课题专题：圆中切线证明与计算
学习目标1、掌握切线的判定及其性质的综合运用，在涉及切线问题时，常连结过切点的半径，得垂直。

2、掌握切线的判定常用以下两种方法：一是“有公共点，连半径，证垂直”，二是“无公共点，作垂线，证半径”。

学习过程课堂笔记
一、课前预习
1、知识点填空：
圆的切线的判定定理：圆的切线的性质定理：
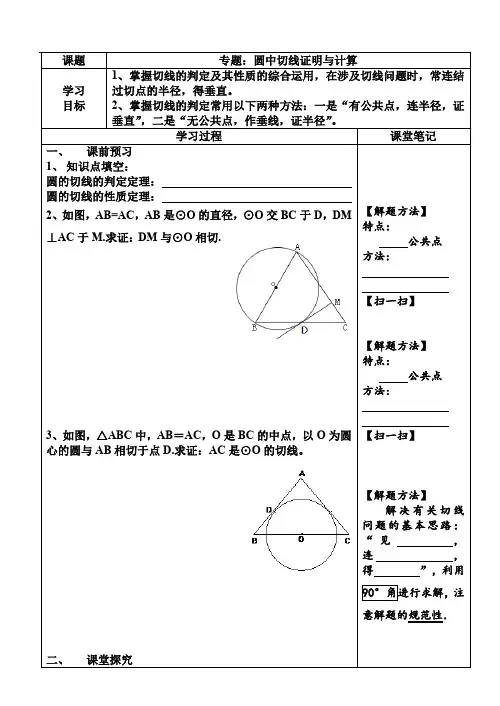
2、如图，AB=AC，AB是⊙O的直径，⊙O交BC于D，DM ⊥AC于M.求证：DM与⊙O相切.
3、如图，△ABC中，AB＝AC，O是BC的中点，以O为圆心的圆与AB相切于点D.求证：AC是⊙O的切线。

二、课堂探究【解题方法】
特点：
公共点
方法:
【扫一扫】
【解题方法】
特点：
公共点
方法:
【扫一扫】
【解题方法】
解决有关切线问题的基本思路：“见，连，得”，利用
90°角进行求解，注
意解题的规范性．。

初中数学知识归纳圆的弦弧与切线初中数学知识归纳: 圆的弦弧与切线圆是数学中一种常见的几何形状，它具有很多特殊的性质和规律。

在圆的学习中，我们不可避免地会接触到弦弧和切线这两个概念。

本文将对初中数学中圆的弦弧与切线的相关知识进行归纳总结。

一、弦弧的概念与性质1. 弦的定义：连接圆上任意两点的线段称为弦。

2. 弦的性质：两个相等的弦所对应的弧是相等的；两个相等的交叉弦所对应的弧互补（即和为180°）。

3. 直径的特殊性：经过圆心的弦称为直径，直径是最长的弦，且恰好把圆分成两个相等的半圆。

4. 弦弧关系：弦所对应的弧可以分为两种情况：a) 圆心角的弧：弦所对应的圆心角等于该弦所对应的弧的度数。

b) 其他弧：弦所对应的弧的度数等于该圆所对应的两个弦所对应弧的度数之和。

即若弦AB对应的弧度数为x°，弦CD对应的弧度数为y°，则弦AB和弦CD所对应的弧的度数之和为x°+y°。

二、切线的概念与性质1. 切线的定义：切线是与圆相切且只与圆交于切点的直线。

2. 切线的性质：切线与半径的关系有以下几条：a) 切线垂直于半径：切线与半径的夹角是90°。

b) 切线定理：切线上的切点到圆心的距离等于切线上任意一点到圆心的距离。

c) 切线与半径的乘积相等：切线长度的平方等于切点到圆心的距离乘以半径的长度。

d) 相交切线定理：如果两条切线相交于圆外一点，则切点与两切线交点所对应的弧度数之和为180°。

三、弦弧和切线的应用1. 利用弦弧和切线的性质，我们可以解决许多与圆相关的数学问题，如求圆的面积、周长、圆心角、弧长等。

2. 弧长公式：弧长等于圆心角度数与半径的乘积的1/360倍，即弧长 = (角度/360) × 2πr，其中r为圆的半径。

3. 弧度制与度制的转换：单位圆（半径为1的圆）上的圆心角度数等于该圆心角所对应弧长的弧度数。

弧长与半径的关系为弧长 = 弧度数 × r。