近四全国卷高考试题不等式选讲大全

2007－ 2019 年全国课标卷不等式选讲试题（ 2007 年宁夏卷）Ｃ（本小题满分10 分）选修4 5 ；不等式选讲设函数 f ( x) 2x 1 x 4 ．（ I）解不等式 f (x) 2 ；（ II）求函数y f (x) 的最小值．（ 2008 年宁夏卷）24、（本小题满分10 分）选修4－ 5：不等式选讲已知函数 f (x) | x 8 | | x 4 | 。

（１）作出函数y f ( x) 的图像；（２）解不等式| x 8 | | x 4 | 2 。

（2009 年宁夏卷）（24）（本小题满分 10 分）选修 4-5：不等式选讲如图，O 为数轴的原点， A,B,M 为数轴上三点， C 为线段 OM 上的动点，设 x 表示 C 与原点的距离， y 表示C 到 A 距离 4 倍与 C 到 B 距离的 6 倍的和 .（1）将 y 表示成 x 的函数；（2）要使 y 的值不超过 70，x 应该在什么范围内取值？（ 2010 年课标全国卷）24.（本小题满分10 分）选修4-5，不等式选项设函数 f ( x) | 2x 4 |1（Ⅰ）画出函数y f ( x) 的图像（Ⅱ）若不等式 f (x) ≤ ax 的解集非空，求 a 的取值范围。

（ 2011 年课标全国卷）24．（本小题满分10 分）选修4- 5：不等式选讲设函数 f (x) | x a |3x ，其中a0．（Ⅰ）当 a=1 时，求不等式 f ( x)3x2的解集．（Ⅱ）若不等式 f ( x)0的解集为｛x|x1} ，求a的值．（ 2012 年课标全国卷）24． ( 本小题满分10 分) 选修4 5 ：不等式选讲已知函数 f ( x) x a x2( 1) 当a3时，求不等式 f ( x) 3 的解集；( 2) 若f (x)x 4 的解集包含[1,2]，求a的取值范围．（2013 年课标全国卷Ⅰ）（24）（本小题满分 10 分）选修 4— 5：不等式选讲已知函数 f ( x) =| 2 x1| | 2x a |, g( x) =x 3 .（Ⅰ）当 a =-2时，求不等式 f ( x) ＜ g ( x) 的解集；（Ⅱ）设a＞ -1,且当xa1a∈ [，)时，f ( x)≤,求的取值范围 .g( x)2 2（2013 年课标全国卷Ⅱ）（24）（本小题满分 10 分）选修 4-5；不等式选讲设 a， b， c 均为正数，且 a + b + c =1，证明：（Ⅰ） ab + bc + ac1；a2b2c21≥≤（ 2014 年课标全国卷Ⅰ）24. （本小题满分10 分）选修4—5 ：不等式选讲若a0, b 011，且ab .a b（Ⅰ）求 a3b3的最小值；（Ⅱ）是否存在a, b ，使得2a3b 6 ？并说明理由.（ 2014 年课标全国卷Ⅱ）24.（本小题满分 10）选修 4-5：不等式选讲设函数 f x= x1x a ( a 0)a（Ⅰ）证明：f x≥ 2；（Ⅱ）若f35，求 a 的取值范围.（2015 年课标全国卷Ⅰ）（24）（本小题满分 10 分）选修 4— 5：不等式选讲已知函数 f ( x) | x 1| 2 | x a |, a0 .（Ⅰ）当 a 1 时，求不等式 f ( x) 1 的解集；（Ⅱ）若 f ( x) 的图像与 x 轴围成的三角形面积大于6，求a的取值范围（ 2015 年课标全国卷Ⅱ）24．（本小题满分10 分）选修 4 - 5：不等式选讲设 a， b，c， d 均为正数，且 a + b = c + d，证明：（ 1）若 ab > cd；则a b c d ；（ 2）a b c d 是 | a b | | c d | 的充要条件。

不等式选讲（原卷版）1．(2021年高考全国乙卷理科)已知函数()3f x x a x =-++．(1)当1a =时，求不等式()6f x ≥的解集; (2)若()f x a >-，求a 的取值范围．2．(2020年高考数学课标Ⅰ卷理科)已知函数()|31|2|1|f x x x =+--．(1)画出()y f x =的图像；(2)求不等式()(1)f x f x >+的解集．3．(2020年高考数学课标Ⅰ卷理科)已知函数2()|21|f x x a x a =-+-+．(1)当2a =时，求不等式()4f x 的解集； (2)若()4f x ，求a 的取值范围．4．(2020年高考数学课标Ⅰ卷理科)设a ，b ，c ∈R ，a +b +c =0，abc =1．(1)证明：ab +bc +ca <0；(2)用max{a ，b ，c }表示a ，b ，c 中的最大值，证明：max{a ，b ，c 5．(2019年高考数学课标Ⅰ卷理科)设,,x y z R ∈，且1x y z ++=．(1)求222(1)(1)(1)x y z -++++的最小值；(2)若2221(2)(1)()3x y z a -+-+-≥成立，证明：3a -≤或1a -≥．6．(2019年高考数学课标全国Ⅰ卷理科)已知函数()()2f x x a x x x a =-+--．()1当1a =时，求不等式()0f x <的解集；()2当(),1x ∈-∞时，()0f x <，求a 的取值范围．7．(2019年高考数学课标全国Ⅰ卷理科)已知a ，b ，c 为正数，且满足1abc =．证明：(1)222111a b c a b c++++≤； (2)333()()()24a b b c c a +++++≥．8．(2018年高考数学课标Ⅰ卷（理）)【选修4—5：不等式选讲】(10分)设函数()211f x x x =++-． (1)画出()y f x =的图象；(2)当[)0,x ∈+∞时，()f x ax b ≤+，求a b +的最小值．9．(2018年高考数学课标Ⅰ卷（理）)[选修4－5：不等式选讲](10分)设函数()5|||2|f x x a x =-+--． (1)当1a =时，求不等式()0f x ≥的解集； (2)若()1f x ≤，求a 的取值范围．10．(2018年高考数学课标卷Ⅰ（理）)[选修4–5：不等式选讲](10分)已知()|1||1|f x x ax =+--．(1)当1a =时，求不等式()1f x >的解集；(2)若(0,1)x ∈时不等式()f x x >成立，求a 的取值范围．11．(2017年高考数学新课标Ⅰ卷理科)[选修4—5:不等式选讲]已知函数,．(1)当时,求不等式的解集;(2)若不等式的解集包含,求的取值范围()24f x x ax =-++()11g x x x =++-1a =()()f x g x ≥()()f x g x ≥[]1,1-a12．(2017年高考数学课标Ⅰ卷理科)[选修4—5：不等式选讲](10分)已知函数． (1)求不等式的解集；(2)若不等式的解集非空，求的取值范围．13．(2017年高考数学课标Ⅰ卷理科)[选修4-5：不等式选讲](10分)已知，证明：(1)；(2)．14．(2016高考数学课标Ⅰ卷理科)选修4—5:不等式选讲已知函数()2f x x a a =-+.(Ⅰ)当2a =时,求不等式()6f x ≤的解集;(Ⅰ)设函数()21g x x =-,当R x ∈时,()()3f x g x +≥,求a 的取值范围. 15．(2016高考数学课标Ⅰ卷理科)(本小题满分10分)选修4—5：不等式选讲已知函数()1122f x x x =-++，M 为不等式()2f x <的解集． (I)求M ；(II)证明：当,a b M ∈时，1a b ab +<+．16．(2016高考数学课标Ⅰ卷理科)(本小题满分10分)选修4—5：不等式选讲已知函数(x)123f x x =+--． (I)画出(x)y f =的图像； (II)求不等式(x)1f >的解集．17．(2015高考数学新课标2理科)(本小题满分10分)选修4-5不等式选讲设,,,a b c d 均为正数，且a b c d +=+，证明： (Ⅰ)若ab cd >>a b c d -<-的充要条件．18．(2015高考数学新课标1理科)(本小题满分10分)选修4—5：不等式选讲()12f x x x =+--()1f x ≥()2f x x x m ≥-+m 330,0,2a b a b >>+=33()()4a b a b ++≥2a b +≤已知函数()12,0f x x x a a =+-->． (Ⅰ)当1a =时，求不等式()1f x >的解集；(Ⅰ)若()f x 的图像与x 轴围成的三角形面积大于6，求a 的取值范围 19．(2014高考数学课标2理科)(本小题满分10)选修4-5：不等式选讲．设函数()f x =1(0)x x a a a++->(Ⅰ)证明：()f x ≥2；(Ⅰ)若()35f <，求a 的取值范围．20．(2014高考数学课标1理科)选修4—5:不等式选讲若,且．(1)求的最小值;(2)是否存在,使得?并说明理由．21．(2013高考数学新课标2理科)设a b c 、、均为正数，且1a b c ++=，证明：(Ⅰ)13ab bc ac ++≤；(Ⅱ)2221a b c b c a++≥ 22．(2013高考数学新课标1理科)选修4—5：不等式选讲已知函数()f x =|21||2|x x a -++,()g x =3x +． (Ⅰ)当a =2时，求不等式()f x ＜()g x 的解集；(Ⅰ)设a ＞-1,且当x ∈[2a -，12)时，()f x ≤()g x ,求a 的取值范围． 23．(2012高考数学新课标理科)选修45-：不等式选讲已知函数()2f x x a x =++-．(1)当3a =-时，求不等式()3f x ≥的解集；(2)若()4f x x ≤-的解集包含[1,2]，求a 的取值范围．0,0ab 11ab a b33ab ,a b 236a b不等式选讲1．(2021年高考全国乙卷理科)已知函数()3f x x a x =-++．(1)当1a =时，求不等式()6f x ≥的解集; (2)若()f x a >-，求a 的取值范围． 【答案】（1）(][),42,-∞-+∞．（2）3,2⎛⎫-+∞ ⎪⎝⎭． 解析：（1）当1a =时，()13f x x x =-++，13x x -++表示数轴上的点到1和3-的距离之和， 则()6f x ≥表示数轴上的点到1和3-的距离之和不小于6，故4x ≤-或2x ≥， 所以()6f x ≥的解集为(][),42,-∞-+∞．（2）依题意()f x a >-，即3a x a x -+>-+恒成立，333x a x x a a x -++-+=≥++，故3a a +>-，所以3a a +>-或3a a +<， 解得32a >-． 所以a 的取值范围是3,2⎛⎫-+∞ ⎪⎝⎭． 【点睛】解绝对值不等式的方法有零点分段法、几何意义法．2．(2020年高考数学课标Ⅰ卷理科)已知函数()|31|2|1|f x x x =+--．(1)画出()y f x =的图像；(2)求不等式()(1)f x f x >+的解集． 【答案】（1）详解解析；（2）7,6⎛⎫-∞-⎪⎝⎭． 【解析】（1）因为()3,1151,1313,3x x f x x x x x ⎧⎪+≥⎪⎪=--<<⎨⎪⎪--≤-⎪⎩，作出图象，如图所示：（2）将函数()f x 的图象向左平移1个单位，可得函数()1f x +的图象，如图所示：由()3511x x --=+-，解得76x =-． 所以不等式()(1)f x f x >+的解集为7,6⎛⎫-∞-⎪⎝⎭． 【点睛】本题主要考查画分段函数的图象，以及利用图象解不等式，意在考查学生的数形结合能力，属于基础题．3．(2020年高考数学课标Ⅱ卷理科)已知函数2()|21|f x x a x a =-+-+．(1)当2a =时，求不等式()4f x 的解集； (2)若()4f x ，求a 的取值范围．【答案】（1）32x x ⎧≤⎨⎩或112x ⎫≥⎬⎭；（2）(][),13,-∞-+∞．解析：（1）当2a =时，()43f x x x =-+-．当3x ≤时，()43724f x x x x =-+-=-≥，解得：32x ≤；当34x <<时，()4314f x x x =-+-=≥，无解；当4x ≥时，()43274f x x x x =-+-=-≥，解得：112x ≥； 综上所述：()4f x ≥的解集为32x x ⎧≤⎨⎩或112x ⎫≥⎬⎭． （2）()()()()22222121211f x x a x a x a x a aa a =-+-+≥---+=-+-=-（当且仅当221a x a -≤≤时取等号）， ()214a ∴-≥，解得：1a ≤-或3a ≥，a ∴的取值范围为(][),13,-∞-+∞．【点睛】本题考查绝对值不等式的求解、利用绝对值三角不等式求解最值的问题，属于常考题型．4．(2020年高考数学课标Ⅲ卷理科)设a ，b ，c ∈R ，a +b +c =0，abc =1．(1)证明：ab +bc +ca <0；(2)用max{a ，b ，c }表示a ，b ，c 中的最大值，证明：max{a ，b ，c 【答案】（1）证明见解析（2）证明见解析． 解析：（1）2222()2220a b c a b c ab ac bc ++=+++++=，()22212ab bc ca a b c ∴++=-++1,,,abc a b c =∴均不为0，则2220a b c ++>，()222120ab bc ca a b c ∴++=-++<； （2）不妨设max{,,}a b c a =，由0,1a b c abc ++==可知，0,0,0a b c ><<，1,a b c a bc =--=，()222322224b c b c bc bc bc a a a bc bc bc++++∴=⋅==≥=．当且仅当b c =时，取等号，a ∴3max{,,}4a b c ．【点睛】本题主要考查了不等式的基本性质以及基本不等式的应用，属于中档题．5．(2019年高考数学课标Ⅲ卷理科)设,,x y z R ∈，且1x y z ++=．(1)求222(1)(1)(1)x y z -++++的最小值；(2)若2221(2)(1)()3x y z a -+-+-≥成立，证明：3a -≤或1a -≥．【答案】【答案】(1)43；(2)见详解． 【官方解析】（1）由于2[(1)(1)(1)]x y z -++++ 222(1)(1)(1)2[(1)(1)(1)(1)(1)(1)]x y z x y y z z x =-+++++-++++++-2223(1)(1)(1)x y z ⎡⎤-++++⎣⎦故由已知得232(1)(1)143()x y z -++++≥，当且仅当511,,333x y z ==-=-时等号成立．所以232(1)(1)(1)x y z -++++的最小值为43． （2）由于2[(2)(1)()]x y z a -+-+- 222(2)(1)()2[(2)(1)(1)()()(2)]x y z a x y y z a z a x =-+-+-+--+--+--2223(2)(1)()x y z a ⎡⎤-+-+-⎣⎦故由已知得2222(2)(2)(1)()3a x y z a +-+-+-，当且仅当4122,,333aa a x y z ---===时等号成立．因此222(2)(1)()x y z a -+-+-的最小值为2(2)3a +由题设知2(2)133a +，解得3a -≤或1a -≥． 【解法2】柯西不等式法(1)22222222[(1)(1)(1)](111)[(1)(1)(1)](1)4x y z x y z x y z -++++++-++++=+++=≥，故2224(1)(1)(1)3x y z -++++≥，当且仅当511,,333x y z ==-=-时等号成立．所以222(1)(1)(1)x y z -++++的最小值为43． (2)2221(2)(1)()3x y z a -+-+-≥，所以222222[(2)(1)()](111)1x y z a -+-+-++≥．当且仅当4122,,333aa a x y z ---===时等号成立． 22222222[(2)(1)()](111)(21)(2)x y z a x y z a a -+-+-++=-+-+-=+成立．所以2(2)1a +≥成立，所以有3a -≤或1a -≥．【点评】本题两问思路一样，既可用基本不等式，也可用柯西不等式求解，属于中档题型． 6．(2019年高考数学课标全国Ⅱ卷理科)已知函数()()2f x x a x x x a =-+--．()1当1a =时，求不等式()0f x <的解集；()2当(),1x ∈-∞时，()0f x <，求a 的取值范围．【答案】()1(),1-∞；()2[)1,+∞ 【官方解析】()1当1a =时，()=|1| +|2|(1)f x x x x x ---.当1x <时，2()2(1)0f x x =--<；当1x ≥时，()0f x ≥. 所以，不等式()0f x <的解集为(,1)-∞.()2因为()=0f a ，所以1a ≥.当1a ≥，(,1)x ∈-∞时，()=() +(2)()=2()(1)<0f x a x x x x a a x x ----- 所以，a 的取值范围是[1,)+∞.【分析】()1根据1a =，将原不等式化为()1210x x x x -+--<，分别讨论1x <，12x <≤，2x ≥三种情况，即可求出结果；()2分别讨论1a ≥和1a <两种情况，即可得出结果.【解析】()1当1a =时，原不等式可化为()1210x x x x -+--<；当1x <时，原不等式可化，即()210x ->，显然成立，此时解集为(),1-∞；当12x <≤时，原不等式可化为()()()1210x x x x -+--<，解得1x <，此时解集为空集； 当2x ≥时，原不等式可化为()()()1210x x x x -+--<，即()210x -<，显然不成立；此时解集为空集；综上，原不等式的解集为(),1-∞；()2当1a ≥时，因为(),1x ∈-∞，所以由()0f x <可得()()()20a x x x x a -+--<，即()()10x a x -->，显然恒成立；所以1a ≥满足题意；当1a <时，()()()2,1()21,x a a x f x x a x x a -<⎧⎪=⎨--<⎪⎩≤，因1a x <≤时， ()0f x <显然不能成立，所以1a <不满足题意；综上，a 的取值范围是[)1,+∞.【点评】本题主要考查含绝对值的不等式，熟记分类讨论的方法求解即可，属于常考题型. 7．(2019年高考数学课标全国Ⅰ卷理科)已知a ，b ，c 为正数，且满足1abc =．证明：(1)222111a b c a b c++++≤； (2)333()()()24a b b c c a +++++≥．【答案】解：（1）因为2222222,2,2a b ab b c bc c a ac +++≥≥≥，又1abc =，故有222111ab bc ca a b c ab bc ca abc a b c ++++++==++≥．所以222111a b c a b c++++≤.（2）因为, , a b c 为正数且1abc =，故有333()()()a b b c c a +++++≥3(+)(+)(+)a b b c a c=324⨯⨯⨯=≥所以333()()()24a b b c c a +++++≥．8．(2018年高考数学课标Ⅲ卷（理）)【选修4—5：不等式选讲】(10分)设函数()211f x x x =++-． (1)画出()y f x =的图象；(2)当[)0,x ∈+∞时，()f x ax b ≤+，求a b +的最小值．【答案】【官方解析】（1）()13,212,123,1x x f x x x x x ⎧-<-⎪⎪⎪=+-≤<⎨⎪≥⎪⎪⎩()y f x =的图像如图所示（2）由（1）知，()y f x =的图像与y 轴交点的纵坐标为2，且各部分所在直线斜率的最大值为3，故当且仅当3a ≥且2b ≥时，()f x ax b ≤+在[)0,+∞成立，因此a b +的最小值为5．【民间解析】（1）()211f x x x =++-3,112,12132x x x x x x ⎧⎪>⎪⎪=+-≤≤⎨⎪⎪-<-⎪⎩，可作出函数()f x 的图象如下图（2）依题意可知()f x ax b ≤+在[)1,+∞上恒成立，在[)0,1上也恒成立 当1x ≥时，()3f x x ax b =≤+恒成立即()30a x b -+≥在[)1,+∞上恒成立 所以30a -≥，且30a b -+≥，此时3a ≥，3a b +≥当01x ≤<时，()2f x x ax b =+≤+即()120a x b -+-≥恒成立 结合3a ≥，可知20b -≥即2b ≥ 综上可知32a b ≥⎧⎨≥⎩，所以当3a =，2b =时，a b +取得最小值5．9．(2018年高考数学课标Ⅱ卷（理）)[选修4－5：不等式选讲](10分)设函数()5|||2|f x x a x =-+--． (1)当1a =时，求不等式()0f x ≥的解集； (2)若()1f x ≤，求a 的取值范围． 【答案】解析：（1）当1a =时， 24,1,()2,12,26, 2.x x f x x x x +-⎧⎪=-<⎨⎪-+>⎩≤ ≤可得()0≥f x 的解集为{}|23≤≤x x -． （2）()1f x ≤等价于|||2|4≥x a x ++-．而|||2||2|≥x a x a ++-+，且当2x =时等号成立，故()1f x ≤等价于|2|4≥a +． 由|2|4≥a +可得6≤a -或2≥a ，所以a 的取值范围是(][),62,-∞-+∞．10．(2018年高考数学课标卷Ⅰ（理）)[选修4–5：不等式选讲](10分)已知()|1||1|f x x ax =+--．(1)当1a =时，求不等式()1f x >的解集；(2)若(0,1)x ∈时不等式()f x x >成立，求a 的取值范围．【答案】解析：（1）当1a =时，()|1||1|f x x x =+--，即2,1,()2,11,2, 1.x f x x x x -≤-⎧⎪=-<<⎨⎪≥⎩故不等式()1f x >的解集为1{|}2x x >．（2）当(0,1)x ∈时|1||1|x ax x +-->成立等价于当(0,1)x ∈时|1|1ax -<成立． 若0a ≤，则当(0,1)x ∈时|1|1ax -≥； 若0a >，|1|1ax -<的解集为20x a<<，所以21a ≥，故02a <≤．综上，a 的取值范围为(0,2]．11．(2017年高考数学新课标Ⅰ卷理科)[选修4—5:不等式选讲]已知函数,()24f x x ax =-++．(1)当时,求不等式的解集;(2)若不等式的解集包含,求的取值范围 2017年高考数学新课标Ⅰ卷理科【答案】(1);(2)． 【分析】(1)将代入,不等式等价于,对按,,讨论,得出最值的解集;(2)当时,．若的解集包含,等价于当时,,则在的最小值必为与之一,所以且,得,所以的取值范围为． 【解析】(1)当时,不等式等价于① 当时,①式化为,无解; 当时,①式化为,从而; 当时,①式化为,从而 所以不等式的解集为 (2)当时, 所以的解集包含,等价于当时, 又在的最小值必为与之一,所以,得． 所以的取值范围为． 【考点】绝对值不等式的解法,恒成立问题 【点评】零点分段法是解答绝对值不等式问题的常用方法,也可以将绝对值函数转化为分段函数,借助图像解题．12．(2017年高考数学课标Ⅲ卷理科)[选修4—5：不等式选讲](10分)已知函数． (1)求不等式的解集；(2)若不等式的解集非空，求的取值范围．【答案】(Ⅰ);(Ⅱ) 【解析】（1）因为()11g x x x =++-1a =()()f x g x ≥()()f x g x ≥[]1,1-a 1x x ⎧⎪-≤≤⎨⎪⎪⎩⎭[]1,1-1a =()()f x g x ≥2|1||1|40x x x x -+++--≤x 1x <-11x -≤≤1x >[1,1]x ∈-()2g x =()()f x g x ≥[1,1]-[]1,1x ∈-()2f x ≥()f x []1,1-()1f -()1f ()12f -≥()12f ≥11a -≤≤a[]1,1-1a =()()f x g x ≥21140x x x x -+++--<1x <-2340x x --≤11x -≤≤220x x --≤11x -≤≤1x >240x x +-≤112x -<≤()()f x g x≥112x x ⎧-⎪-≤≤⎨⎪⎪⎩⎭[]1,1x ∈-()2g x =()()f x g x ≥[]1,1-[]1,1x ∈-()2f x ≥()f x []1,1-()1f -()1f ()()1212f f -≥⎧⎪⎨≥⎪⎩11a -≤≤a []1,1-()12f x x x =+--()1f x ≥()2f x x x m ≥-+m {}1x x ≥5-，4⎛⎤∞ ⎥⎝⎦()3, 11221, 123, 2x f x x x x x x -<-⎧⎪=+--=-≤≤⎨⎪>⎩所以不等式等价于或或由无解；由；由 综上可得不等式的解集为．（2）解法一：先求不等式的解集为空集时的取值范围不等式的解集为空集等价于不等式恒成立记，则当时，当时，当时， 所以 所以不等式的解集为空集时， 所以不等式的解集非空时，的取值范围为．解法二：原式等价于存在，使成立，即设由（1）知当时，，其开口向下，对称轴 ()1f x ≥131x <-⎧⎨-≥⎩12211x x -≤≤⎧⎨-≥⎩231x >⎧⎨≥⎩131x <-⎧⎨-≥⎩⇒x 1222x x -≤≤⎧⎨≥⎩12x ⇒≤≤231x >⎧⎨≥⎩2x ⇒≥()1f x ≥[)1,+∞()2f x x x m ≥-+m ()2f x x x m ≥-+()2m f x x x >-+()()2F x f x x x =-+2223, 131, 123, 2x x x x x x x x x ⎧-+-<-⎪-+-≤≤⎨⎪-++>⎩()max m F x >⎡⎤⎣⎦1x <-()()2211131524F x x x x F ⎛⎫=-+-=---<-=- ⎪⎝⎭12x -≤≤()223535312424F x x x x F ⎛⎫⎛⎫=-+-=--+≤= ⎪ ⎪⎝⎭⎝⎭2x >()()2211332124F x x x x F ⎛⎫=-++=--+<= ⎪⎝⎭()max 3524F x F ⎛⎫==⎡⎤⎪⎣⎦⎝⎭()2f x x x m ≥-+54m >()2f x x x m ≥-+m 5,4⎛⎤-∞ ⎥⎝⎦x R ∈2()f x x x m -+≥2max [()]f x x x m -+≥2()()g x f x x x =-+2223,1()31,123,2x x x g x x x x x x x ⎧-+-≤-⎪=-+--<<⎨⎪-++≥⎩1x ≤-2()3g x x x =-+-112x =>-所以当时，，其开口向下，对称轴为 所以 当时，，其开口向下，对称轴为 所以 综上 所以的取值范围为．【考点】绝对值不等式的解法 【点评】绝对值不等式的解法有三种：法一：利用绝对值不等式的几何意义求解，体现了数形结合的思想； 法二：利用“零点分段法”求解，体现了分类讨论的思想；法三：通过构造函数，利用函数的图象求解，体现了函数与方程的思想．13．(2017年高考数学课标Ⅱ卷理科)[选修4-5：不等式选讲](10分)已知，证明：(1)； (2)．【答案】【命题意图】不等式证明，柯西不等式 【基本解法】（1）解法一：由柯西不等式得：解法二：解法三：又，所以．当时，等号成立．()()11135g x g ≤-=---=-12x -<<()231g x x x =-+-32x =()399512424g x g ⎛⎫≤=-+-= ⎪⎝⎭2x ≥()23g x x x =-++12x =()()24231g x g ≤=-++=()max 54g x =⎡⎤⎣⎦m 5,4⎛⎤-∞ ⎥⎝⎦330,0,2a b a b >>+=33()()4a b a b ++≥2a b +≤55222222332()()))()4a b a b a b a b ⎡⎤⎡⎤++=+⋅+≥+=⎣⎦⎣⎦5566553325533()()()2a b a b a b ab a b a b ab a b a b++=+++=+++-33233332()2()4a b a b a b ≥++=+=()()()()()2555533553342a b a b a b a b a bab a b a b ++-=++-+=+-0,0a b >>()255332220ab a b a b ab a b +-=-≥a b =所以，，即．（2）解法一：由及得所以．解法二：（反证法）假设，则，两边同时立方得：，即，因为，所以，即，矛盾，所以假设不成立，即．解法三：因为，所以：．又，所以: 。

高三数学不等式选讲试题1.已知函数.（Ⅰ）解不等式: ；（Ⅱ）当时, 不等式恒成立,求实数a的取值范围.【答案】（1）；（2）.【解析】本题主要考查绝对值不等式的解法、不等式的性质等基础知识，考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问，由于，可以转化为，所以分3种情况，，进行讨论去掉绝对值符号解不等式；第二问，，所以利用不等式的性质得到最大值代入上式，解不等式，得到a的取值范围.试题解析：（Ⅰ）原不等式等价于:当时, ,即；当时, ,即；当时, ,即.综上所述,原不等式的解集为. （5分）（Ⅱ）当时,=所以（10分）【考点】绝对值不等式的解法、不等式的性质.2.不等式的解集是【答案】【解析】原不等式可化为，解得.考点:绝对值不等式解法3.若不等式|x-a|-|x|<2－a2对x∈R恒成立，则实数a的取值范围是。

【答案】【解析】,所以原式恒成立，即,即,解得【考点】不等式恒成立问题4.对于，当非零实数a，b满足，且使最大时，的最小值为 .【答案】【解析】法一：判别式法：令，则，代入到中，得，即……①因为关于的二次方程①有实根，所以，可得，取最大值时，或，当时，，当时，，综上可知当时，法二：柯西不等式：由可得：，当且仅当时取等号，即时，取等号，这时或当时，，当时，，综上可知当时，【考点】柯西不等式.5.（5分）（2011•陕西）（请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）A．（不等式选做题）若不等式|x+1|+|x﹣2|≥a对任意x∈R恒成立，则a的取值范围是．B．（几何证明选做题）如图，∠B=∠D，AE⊥BC，∠ACD=90°，且AB=6，AC=4，AD=12，则AE= ．C．（坐标系与参数方程选做题）直角坐标系xoy中，以原点为极点，x轴的正半轴为极轴建极坐标系，设点A，B分别在曲线C1：（θ为参数）和曲线C2：p=1上，则|AB|的最小值为．【答案】（﹣∞，3] 2 1【解析】A．首先分析题目已知不等式|x+1|+|x﹣2|≥a恒成立，求a的取值范围，即需要a小于等于|x+1|+|x﹣2|的最小值即可．对于求|x+1|+|x﹣2|的最小值，可以分析它几何意义：在数轴上点x 到点﹣1的距离加上点x到点2的距离．分析得当x在﹣1和2之间的时候，取最小值，即可得到答案；B．先证明Rt△ABE∽Rt△ADC，然后根据相似建立等式关系，求出所求即可；C．先根据ρ2=x2+y2，sin2+cos2θ=1将极坐标方程和参数方程化成直角坐标方程，根据当两点连线经过两圆心时|AB|的最小，从而最小值为两圆心距离减去两半径．解：A．已知不等式|x+1|+|x﹣2|≥a恒成立，即需要a小于等于|x+1|+|x﹣2|的最小值即可．故设函数y=|x+1|+|x﹣2|．设﹣1、2、x在数轴上所对应的点分别是A、B、P．则函数y=|x+1|+|x﹣2|的含义是P到A的距离与P到B的距离的和．可以分析到当P在A和B的中间的时候，距离和为线段AB的长度，此时最小．即：y=|x+1|+|x﹣2|=|PA|+|PB|≥|AB|=3．即|x+1|+|x﹣2|的最小值为3．即：k≤3．故答案为：（﹣∞，3]．B．∵∠B=∠D，AE⊥BC，∠ACD=90°∴Rt△ABE∽Rt△ADC而AB=6，AC=4，AD=12，根据AD•AE=AB•AC解得：AE=2，故答案为：2C．消去参数θ得，（x﹣3）2+y2=1而p=1，则直角坐标方程为x2+y2=1，点A在圆（x﹣3）2+y2=1上，点B在圆x2+y2=1上则|AB|的最小值为1．故答案为：1点评：A题主要考查不等式恒成立的问题，其中涉及到绝对值不等式求最值的问题，对于y=|x﹣a|+|x﹣b|类型的函数可以用分析几何意义的方法求最值．本题还考查了三角形相似和圆的参数方程等有关知识，同时考查了转化与划归的思想，属于基础题．6.不等式的解集为 .【答案】.【解析】解不等式，得，解得，故不等式的解集为.【考点】绝对值不等式的求解7.已知函数.（1）解不等式：；（2）当时，不等式恒成立，求实数的取值范围.【答案】（1）；（2）【解析】（1）由函数，及解不等式，通过将x的区间分为3类可解得结论.（2）由当时，不等式恒成立，令函数.所以原题等价于，由.通过绝对值不等式的公式即可得到函数的最大值，再通过解绝对值不等式可得结论.（1）原不等式等价于：当时，，即.当时，，即当时，，即.综上所述，原不等式的解集为. 4分（2）当时，=所以 7分【考点】1.绝对值不等式.2.恒成立问题.3.分类的数学思想.8.阅读：已知、，，求的最小值.解法如下：，当且仅当，即时取到等号，则的最小值为.应用上述解法，求解下列问题：（1）已知，，求的最小值；（2）已知，求函数的最小值；（3）已知正数、、，，求证：.【答案】（1）9；（2）18；（3）证明见解析.【解析】本题关键是阅读给定的材料，弄懂弄清给定材料提供的方法（“1”的代换），并加以运用.主要就是，展开后就可应用基本不等式求得最值.（1）；（2）虽然没有已知的“1”，但观察求值式子的分母，可以凑配出“1”：，因此有，展开后即可应用基本不等式；（3）观察求证式的分母，结合已知有，因此有此式中关键是凑配出基本不等式所需要的两项，如与合并相加利用基本不等式有，从而最终得出.（1）， 2分而，当且仅当时取到等号，则，即的最小值为. 5分（2）， 7分而，，当且仅当，即时取到等号，则，所以函数的最小值为. 10分（3）当且仅当时取到等号，则. 16分【考点】阅读材料问题，“1”的代换，基本不等式.9.（2012•广东）不等式|x+2|﹣|x|≤1的解集为_________．【答案】【解析】∵|x+2|﹣|x|=∴x≥0时，不等式|x+2|﹣|x|≤1无解；当﹣2＜x＜0时，由2x+2≤1解得x≤，即有﹣2＜x≤；当x≤﹣2，不等式|x+2|﹣|x|≤1恒成立，综上知不等式|x+2|﹣|x|≤1的解集为故答案为10.已知函数f(x)=|x－a|,其中a>1.(1)当a=2时,求不等式f(x)≥4－|x－4|的解集;(2)已知关于x的不等式|f(2x+a)－2f(x)|≤2的解集为{x|1≤x≤2},求a的值.【答案】(1){x|x≤1或x≥5}.(2)3【解析】(1)当a=2时, f(x)+|x－4|=当x≤2时,由f(x)≥4－|x－4|得－2x+6≥4,解得x≤1;当2<x<4时, f(x)≥4－|x－4|无解;当x≥4时,由f(x)≥4－|x－4|得2x－6≥4,解得x≥5;所以f(x)≥4－|x－4|的解集为{x|x≤1或x≥5}.(2)记h(x)=f(2x+a)－2f(x),则h(x)=由|h(x)|≤2,解得≤x≤又已知|h(x)|≤2的解集为{x|1≤x≤2}.所以=1且=2于是a=3.11.设a>1>b>-1,则下列不等式中恒成立的是()A．<B．>C．a>b2D．a2>2b【答案】C【解析】选C.令a=2,b=-,验证可得选项A不正确,令a=2,b=,则B不正确,若a=1.1,b=0.9,则D 不正确,对选项C,由-1<b<1得:0≤b2<1,又a>1,故b2<a,故C项正确.12.已知a,b,c为三角形的三边长,则a2与ab+ac的大小关系是.【答案】a2<ab+ac【解析】因为a,b,c为三角形的三边长,所以a<b+c,又因为a>0,所以a2<a(b+c),即a2<ab+ac.13.设x,y∈R,且x+y=5,则3x+3y的最小值为()A．10B．6C．4D．18【答案】D【解析】选D.3x+3y≥2=2=2=18,当且仅当x=y=2.5时,等号成立.14.已知点P(x,y)在经过A(3,0),B(1,1)两点的直线上,那么2x+4y的最小值为()A．2B．4C．16D．不存在【答案】B【解析】选B.过A,B两点的直线方程为y=-(x-3),所以x=3-2y,所以2x+4y=+4y≥4,当且仅当=4y时,等号成立.,x,y为变量,a,b为常数,且a+b=10,+=1,x+y的最小值为18,求a,b.15.已知a,b,x,y∈R+【答案】或【解析】因为x+y=(x+y)=a+b++≥a+b+2=(+)2,=(+)2=18,当且仅当=时取等号.又(x+y)min即a+b+2=18,①又a+b=10,②由①②可得或16.若关于x的不等式|a|≥|x+1|+|x-2|存在实数解,则实数a的取值范围是.【答案】(-∞,-3]∪[3,+∞)【解析】因为f (x)=|x+1|+|x-2|=所以f(x)≥3,要使|a|≥|x+1|+|x-2|有解,故|a|≥3,即a≤-3或a≥3.17.已知a、b、m、n均为正数，且a＋b＝1，mn＝2，求(am＋bn)(bm＋an)的最小值．【答案】2【解析】利用柯西不等式求解，(am＋bn)(an＋bm)≥()2＝mn·(a＋b)2＝2·1＝2，且仅当即m＝n时取最小值2.18.已知x，y，z∈R＋，且x＋y＋z＝1(1)若2x2＋3y2＋6z2＝1，求x，y，z的值．(2)若2x2＋3y2＋tz2≥1恒成立，求正数t的取值范围．【答案】（1）x＝，y＝，z＝（2）t≥6【解析】(1)∵(2x2＋3y2＋6z2)()≥(x＋y＋z)2＝1，当且仅当时取“＝”．∴2x＝3y＝6z，又∵x＋y＋z＝1，∴x＝，y＝，z＝.＝.(2)∵(2x2＋3y2＋tz2)≥(x＋y＋z)2＝1，∴(2x2＋3y2＋tz2)min∵2x2＋3y2＋tz2≥1恒成立，∴≥1.∴t≥6.19.若对恒成立,则实数的取值范围是___________.【答案】【解析】当为偶数时，，而；当为奇数时，，而.所以的取值范围是.【考点】不等式.20.若关于x的不等式的解集为(-1,4)，则实数a的值为_________.【答案】【解析】由已知得，，，当时，不等式解集为，故，无解；当时，不等式解集为，故，解得．【考点】绝对值不等式解法．21.已知函数，m∈R，且的解集为．（1）求的值；（2）若，且，求的最小值.+【答案】（1）.（2）的最小值为9.【解析】（1）由已知，得到所以根据的解集是，得到.（2）由(1)知，，由柯西不等式即得所求.试题解析：（1）因为，所以.所以又的解集是，故. 5分（2）由(1)知，，由柯西不等式得∴的最小值为9 10分【考点】绝对值不等式解法，柯西不等式.22.已知a,b,c,d均为正实数,且a+b+c+d=1,求证:+++≥.【答案】见解析【解析】证明：因为[(1+a)+(1+b)+(1+c)+(1+d)]·(+++)≥(·+·+·+·)2=(a+b+c+d)2=1,当且仅当===即a=b=c=d=时取等号.又(1+a)+(1+b)+(1+c)+(1+d)=4+(a+b+c+d)=5,所以5(+++)≥1.所以+++≥.23.设不等式|x－2|<a(a∈N*)的解集为A，且∈A，∉A.(1)求a的值；(2)求函数f(x)＝|x＋a|＋|x－2|的最小值．【答案】（1）a＝1（2）3.【解析】(1)因为∈A，且∉A，所以<a，且≥a，解得<a≤.又因为a∈N*，所以a＝1.(2)因为|x＋1|＋|x－2|≥|(x＋1)－(x－2)|＝3，当且仅当(x＋1)(x－2)≤0，即－1≤x≤2时取到等号，所以f(x)的最小值为3.24. (1)设x≥1，y≥1，证明x＋y＋≤＋＋xy；(2)1＜a≤b≤c，证明loga b＋logbc＋logca≤logba＋logcb＋logac.【答案】（1）见解析（2）见解析【解析】(1)由于x≥1，y≥1，要证x＋y＋≤＋＋xy，只需证xy(x＋y)＋1≤y＋x＋(xy)2.因为[y＋x＋(xy)2]－[xy(x＋y)＋1]＝[(xy)2－1]－[xy(x＋y)－(x＋y)]＝(xy＋1)(xy－1)－(x＋y)(xy－1)＝(xy－1)(xy－x－y＋1)＝(xy－1)(x－1)(y－1)．由条件x≥1，y≥1，得(xy－1)(x－1)(y－1)≥0，从而所要证明的不等式成立．(2)设loga b＝x，logbc＝y，由对数的换底公式得logca＝，logba＝，logcb＝，logac＝xy.于是，所要证明的不等式即为x＋y＋≤＋＋xy.其中x＝loga b≥1，y＝logbc≥1.故由(1)可知所要证明的不等式成立．25.已知函数f(x)＝|2x－a|＋a.若不等式f(x)≤6的解集为{x|－2≤x≤3}，则实数a的值为________．【答案】a＝1【解析】由|2x－a|＋a≤6得，|2x－a|≤6－a，∴a－6≤2x－a≤6－a，即a－3≤x≤3，∴a－3＝－2，∴a＝1.26.若正数x，y满足x＋3y＝5xy，则3x＋4y的最小值是()．A．B．C．5D．6【答案】C【解析】∵x>0，y>0，由x＋3y＝5xy，得＝5.∴5(3x＋4y)＝(3x＋4y) ＝13＋≥13＋2＝25.因此3x＋4y≥5，当且仅当x＝2y时等号成立．∴当x＝1，y＝时，3x＋4y的最小值为5.27.设实数均不小于1，且，则的最小值是．（是指四个数中最大的一个）【答案】9【解析】设，则，当时上式两等号都能取到，所以的最小值为9.【考点】多元函数最值的求法.28.已知（x+1）n=a0+a1（x﹣1）+a2（x﹣1）+a3（x﹣1）3+…+an（x﹣1）n，（其中n∈N*）（1）求a及；（2）试比较Sn与（n﹣2）2n+2n2的大小，并说明理由．【答案】（1）Sn=3n﹣2n（2）当n=1时，3n＞（n﹣1）2n+2n2；当n=2，3时，3n＜（n﹣1）2n+2n2；当n≥4，n∈N*时，3n＞（n﹣1）2n+2n2【解析】（1）令x=1，则a=2n，令x=2，则，∴Sn=3n﹣2n；（3分）（2）要比较Sn与（n﹣2）2n+2n2的大小，即比较：3n与（n﹣1）2n+2n2的大小，当n=1时，3n＞（n﹣1）2n+2n2；当n=2，3时，3n＜（n﹣1）2n+2n2；当n=4，5时，3n＞（n﹣1）2n+2n2；（5分）猜想：当n≥4时n≥4时，3n＞（n﹣1）2n+2n2，下面用数学归纳法证明：由上述过程可知，n=4n=4时结论成立，假设当n=k（k≥4）n=k，（k≥4）时结论成立，即3n＞（n﹣1）2n+2n2，两边同乘以3 得：3k+1＞3[（k﹣1）2k+2k2]=k2k+1+2（k+1）2+[（k﹣3）2k+4k2﹣4k﹣2]而（k﹣3）2k+4k2﹣4k﹣2=（k﹣3）2k+4（k2﹣k﹣2）+6=（k﹣2）2k+4（k﹣2）（k+1）+6＞0∴3k+1＞[（k+1）﹣1]2k+1+2（k+1）2即n=k+1时结论也成立，∴当n≥4时，3n＞（n﹣1）2n+2n2成立．综上得，当n=1时，3n＞（n﹣1）2n+2n2；当n=2，3时，3n＜（n﹣1）2n+2n2；当n≥4，n∈N*时，3n＞（n﹣1）2n+2n2﹣﹣（10分）【考点】用数学归纳法证明不等式；数列的求和；二项式定理的应用点评：本题是中档题，考查与n有关的命题，通过赋值法解答固定项，前n项和，以及数学归纳法的应用，考查逻辑推理能力，计算能力，常考题型29.选修4—5：不等式选讲已知函数（1）若不等式的解集为，求实数a，m的值。

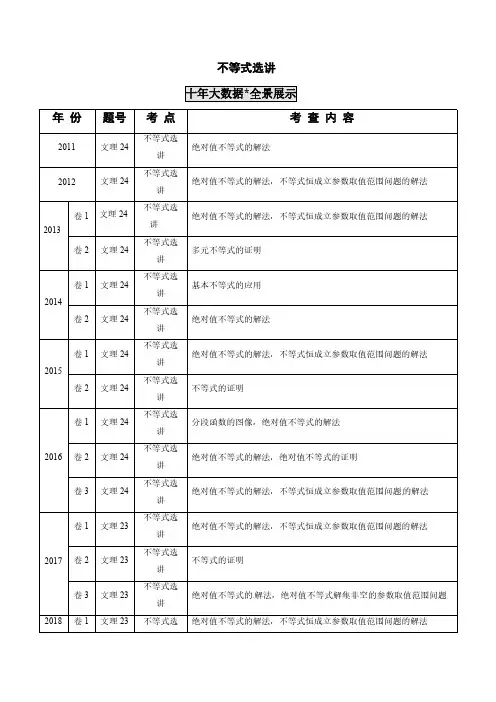
不等式选讲年份题号考点考查内容2011文理24不等式选讲绝对值不等式的解法2012文理24不等式选讲绝对值不等式的解法，不等式恒成立参数取值范围问题的解法2013卷1文理24不等式选讲绝对值不等式的解法，不等式恒成立参数取值范围问题的解法卷2文理24不等式选讲多元不等式的证明2014卷1文理24不等式选讲基本不等式的应用卷2文理24不等式选讲绝对值不等式的解法2015卷1文理24不等式选讲绝对值不等式的解法，不等式恒成立参数取值范围问题的解法卷2文理24不等式选讲不等式的证明2016卷1文理24不等式选讲分段函数的图像，绝对值不等式的解法卷2文理24不等式选讲绝对值不等式的解法，绝对值不等式的证明卷3文理24不等式选讲绝对值不等式的解法，不等式恒成立参数取值范围问题的解法2017卷1文理23不等式选讲绝对值不等式的解法，不等式恒成立参数取值范围问题的解法卷2文理23不等式选讲不等式的证明卷3文理23不等式选讲绝对值不等式的解法，绝对值不等式解集非空的参数取值范围问题2018卷1文理23不等式选绝对值不等式的解法，不等式恒成立参数取值范围问题的解法讲卷2文理23不等式选讲绝对值不等式的解法，不等式恒成立参数取值范围问题的解法卷3文理23不等式选讲绝对值函数的图象，不等式恒成立参数最值问题的解法2019卷1文理23不等式选讲三元条件不等式的证明卷2文理23不等式选讲绝对值不等式的解法，不等式恒成立参数取值范围问题的解法卷3文理23不等式选讲三元条件最值问题的解法，三元条件不等式的证明2020卷1文理23不等式选讲绝对值函数的图像，绝对值不等式的解法卷2文理23不等式选讲绝对值不等式的解法，不等式恒成立参数取值范围问题的解法卷3文理23不等式选讲三元条件不等式的证明考点出现频率2021年预测考点120绝对值不等式的求解23次考4次2021年主要考查绝对值不等式的解法、绝对值不等式的证明，不等式恒成立参数取值范围问题的解法等．考点121含绝对值不等式的恒成立问题23次考12次考点122不等式的证明23次考7次考点120绝对值不等式的求解1．(2020全国Ⅰ文理22)已知函数()3121f x x x =+--．(1)画出()y f x =的图像；(2)求不等式()()1f x f x >+的解集．【解析】(1)∵()3,1151,1313,3x x f x x x x x ⎧⎪+≥⎪⎪=--<<⎨⎪⎪--≤-⎪⎩，作出图像，如图所示：(2)将函数()f x 的图像向左平移1个单位，可得函数()1f x +的图像，如图所示：由()3511x x --=+-，解得76x =-，∴不等式的解集为7,6⎛⎫-∞- ⎪⎝⎭．2．(2020江苏23)设x ∈R ，解不等式2|1|||4x x ++≤．【答案】22,3⎡⎤-⎢⎥⎣⎦【思路导引】根据绝对值定义化为三个不等式组，解得结果．【解析】1224x x x <-⎧⎨---≤⎩ 或10224x x x -≤≤⎧⎨+-≤⎩或0224x x x >⎧⎨++≤⎩，21x ∴-≤<-或10x -≤≤或203x <≤，∴解集为22,3⎡⎤-⎢⎥⎣⎦．3．(2016全国I 文理)已知函数()|1||23|f x x x =+--．(I)在图中画出()y f x =的图像；(II)求不等式|()|1f x >的解集．【解析】(1)如图所示：(2)()4133212342x x f x x x x x ⎧⎪--⎪⎪=--<<⎨⎪⎪-⎪⎩，≤，，≥，()1f x >．当1x -≤，41x ->，解得5x >或3x <，1x -∴≤；当312x -<<，321x ->，解得1x >或13x <，113x -<<∴或312x <<；当32x ≥，41x ->，解得5x >或3x <，332x <∴≤或5x >．综上，13x <或13x <<或5x >，()1f x >∴，解集为()()11353⎛⎫-∞+∞ ⎪⎝⎭ ，，，．4．(2014全国II 文理)设函数()f x =1(0)x x a a a++->(Ⅰ)证明：()f x ≥2；(Ⅱ)若()35f <，求a 的取值范围．【解析】(I)由0a >，有()f x 111()2x x a x x a a a a a=++-≥+--=+≥，∴()f x ≥2．(Ⅱ)1(3)33f a a=++-．当时a ＞3时，(3)f =1a a+，由(3)f ＜5得3＜a ＜5212；当0＜a ≤3时，(3)f =16a a-+，由(3)f ＜5得12＜a ≤3．综上：a 的取值范围是(152+，5212+)．5．(2011新课标文理)设函数()3f x x a x =-+，其中0a >．(Ⅰ)当1a =时，求不等式()32f x x ≥+的解集；(Ⅱ)若不等式()0f x ≤的解集为{}|1x x ≤-，求a 的值．【解析】(Ⅰ)当1a =时，()32f x x ≥+可化为|1|2x -≥，由此可得3x ≥或1x ≤-．故不等式()32f x x ≥+的解集为{|3x x ≥或1}x ≤-．(Ⅱ)由()0f x ≤得30x a x -+≤，此不等式化为不等式组30x ax a x ≥⎧⎨-+≤⎩或30x aa x x ≤⎧⎨-+≤⎩，即4x a a x ⎧⎪⎨⎪⎩≥≤或2x aax ⎧⎪⎨-⎪⎩≤≤，因为0a >，∴不等式组的解集为{}|2a x x ≤-，由题设可得2a-=1-，故2a =．考点121含绝对值不等式的恒成立问题6．(2020全国Ⅱ文理22)已知函数()221f x x a x a =-+-+．(1)当2a =时，求不等式()4f x ≥的解集；(2)若()4f x ≥，求a 的取值范围．【答案】(1)32x x ⎧≤⎨⎩或112x ⎫≥⎬⎭；(2)(][),13,-∞-+∞ ．【思路导引】(1)分别在3x ≤、34x <<和4x ≥三种情况下解不等式求得结果；(2)利用绝对值三角不等式可得到()()21f x a ≥-，由此构造不等式求得结果．【解析】(1)当2a =时，()43f x x x =-+-．当3x ≤时，()43724f x x x x =-+-=-≥，解得：32x ≤；当34x <<时，()4314f x x x =-+-=≥，无解；当4x ≥时，()43274f x x x x =-+-=-≥，解得：112x ≥；综上所述：()4f x ≥的解集为32x x ⎧≤⎨⎩或112x ⎫≥⎬⎭．(2)()()()()22222121211f x x a x a x ax a a a a =-+-+≥---+=-+-=-(当且仅当221a x a -≤≤时取等号)，()214a ∴-≥，解得：1a ≤-或3a ≥，a ∴的取值范围为(][),13,-∞-+∞ ．7．(2019全国II 文理23)[选修4-5：不等式选讲](10分)已知()|||2|().f x x a x x x a =-+--(1)当1a =时，求不等式()0f x <的解集；(2)若(,1)x ∈-∞时，()0f x <，求a 的取值范围．【解析】(1)当a=1时，()=|1| +|2|(1)f x x x x x ---．当1x <时，2()2(1)0f x x =--<；当1x ≥时，()0f x ≥，∴不等式()0f x <的解集为(,1)-∞．(2)因为()=0f a ，∴1a ≥．当1a ≥，(,1)x ∈-∞时，()=() +(2)()=2()(1)<0f x a x x x x a a x x -----∴a 的取值范围是[1,)+∞．8．(2018全国Ⅰ文理)已知()|1||1|f x x ax =+--．(1)当1a =时，求不等式()1f x >的解集；(2)若(0,1)x ∈时不等式()f x x >成立，求a 的取值范围．【解析】(1)当1a =时，()|1||1|f x x x =+--，即2,1,()2,11,2, 1.--⎧⎪=-<<⎨⎪⎩≤≥x f x x x x 故不等式()1f x >的解集为1{|}2x x >．(2)当(0,1)x ∈时|1||1|x ax x +-->成立等价于当(0,1)x ∈时|1|1ax -<成立．若0≤a ，则当(0,1)x ∈时|1|1-≥ax ；若0a >，|1|1ax -<的解集为20x a <<，∴21≥a，故02<≤a ．综上，a 的取值范围为(0,2]．9．(2018全国Ⅱ文理)设函数()5|||2|=-+--f x x a x ．(1)当1a =时，求不等式()0≥f x 的解集；(2)若()1≤f x ，求a 的取值范围．【解析】(1)当1=a 时，24,1,()2,12,26, 2.+-⎧⎪=-<⎨⎪-+>⎩≤≤x x f x x x x 可得()0≥f x 的解集为{|23}-≤≤x x ．(2)()1≤f x 等价于|||2|4++-≥x a x ．而|||2||2|++-+≥x a x a ，且当2=x 时等号成立．故()1≤f x 等价于|2|4+≥a ．由|2|4+≥a 可得6-≤a 或2≥a ，∴a 的取值范围是(,6][2,)-∞-+∞ ．10．(2018全国Ⅲ文理)设函数()|21||1|f x x x =++-．(1)画出()y f x =的图像；(2)当[0,)x ∈+∞时，()f x ax b +≤，求a b +的最小值．【解析】(1)13,,21()2,1,23, 1.x x f x x x x x ⎧-<-⎪⎪⎪=+-<⎨⎪⎪⎪⎩≤≥()y f x =的图像如图所示．(2)由(1)知，()y f x =的图像与y 轴交点的纵坐标为2，且各部分所在直线斜率的最大值为3，故当且仅当3a ≥且2b ≥时，()f x ax b +≤在[0,)+∞成立，因此a b +的最小值为5．11．(2018江苏)若x ，y ，z 为实数，且226x y z ++=，求222x y z ++的最小值．【解析】由柯西不等式，得2222222()(122)(22)x y z x y z ++++++≥．因为22=6x y z ++，∴2224x y z ++≥，当且仅当122x y z ==时，不等式取等号，此时244333x y z ===，，，∴222x y z ++的最小值为4．12．(2017全国Ⅰ文理)已知函数2()4f x x ax =-++，()|1||1|g x x x =++-．(1)当1a =时，求不等式()()f x g x ≥的解集；(2)若不等式()()f x g x ≥的解集包含[1,1]-，求a 的取值范围．【解析】(1)当1a =时，不等式()()f x g x ≥等价于2|1||1|40x x x x -+++--≤．①当1x <-时，①式化为2340x x --≤，无解；当11x -≤≤时，①式化为220x x --≤，从而11x -≤≤；当1x >时，①式化为240x x +-≤，从而11712x -+<≤，∴()()f x g x ≥的解集为117{|1}2x x -+-<≤．(2)当[1,1]x ∈-时，()2g x =，∴()()f x g x ≥的解集包含[1,1]-，等价于当[1,1]x ∈-时()2f x ≥．又()f x 在[1,1]-的最小值必为(1)f -与(1)f 之一，∴(1)2f -≥且(1)2f ≥，得11a -≤≤，∴a 的取值范围为[1,1]-．13．(2017全国Ⅲ文理)已知函数()|1||2|f x x x =+--．(1)求不等式()1f x ≥的解集；(2)若不等式2()f x x x m -+≥的解集非空，求m 的取值范围．【解析】(1)3,1()21,123,2x f x x x x -<-⎧⎪=--⎨⎪>⎩≤≤，当1x <-时，()f x 1≥无解；当x -12≤≤时，由()f x 1≥得，x -211≥，解得x 12≤≤；当＞2x 时，由()f x 1≥解得＞2x ．∴()f x 1≥的解集为{}x x 1≥．(2)由()f x x x m -+2≥得m x x x x +---+212≤，而x x x x x x x x +---+--+2212+1+2≤x ⎛⎫ ⎪⎝⎭2355=--+244≤，且当32x =时，2512=4x x x x +---+，故m 的取值范围为5-，4⎛⎤∞ ⎥⎝⎦．14．(2016全国III 文理)已知函数()|2|f x x a a =-+(Ⅰ)当a=2时，求不等式()6f x ≤的解集；(Ⅱ)设函数()|21|g x x =-，当x ∈R 时，()()3f x g x +≥，求a 的取值范围．【解析】(Ⅰ)当2a =时，()|22|2f x x =-+．解不等式|22|26x -+ ，得13x - ，因此()6f x ≤的解集为{|13}x x - ．(Ⅱ)当x R ∈时，()()|2||12|f xg x x a a x +=-++-|212|x a x a -+-+ |1|a a =-+，当12x =时等号成立，∴当x R ∈时，()()3f x g x + 等价于|1|3a a -+ ．①当1a 时，①等价于13a a -+ ，无解．当1a >时，①等价于13a a -+ ，解得2a ．∴a 的取值范围是[2,)+∞．15．(2015全国I 文理)已知函数()|1|2||f x x x a =+--，0a >．(Ⅰ)当1a =时，求不等式()1f x >的解集；(Ⅱ)若()f x 的图像与x 轴围成的三角形面积大于6，求a 的取值范围．【解析】(Ⅰ)当1a =时，不等式()1f x >化为|1|2|1|10x x +--->，当1x -≤时，不等式化为40x ->，无解；当11x -<<时，不等式化为320x ->，解得213x <<；当1x ≥时，不等式化为20x -+>，解得12x <≤．∴()1f x >的解集为2{|2}3x x <<．(Ⅱ)有题设可得，12,1()312,112,x a x f x x a x a x a x a --<-⎧⎪=+--⎨⎪-++>⎩≤≤，∴函数()f x 图象与x 轴围成的三角形的三个顶点分别为21(,0),(21,0),(,1)3a A B a C a a -++，ABC ∆的面积为22(1)3a +．有题设得22(1)63a +>，故2a >．∴a 的取值范围为(2,)+∞．16．(2014全国I 文理)若0,0ab >>，且11a b +=．(Ⅰ)求33a b +的最小值；(Ⅱ)是否存在,a b ，使得236a b +=？并说明理由．【解析】(I)11a b =+≥，得2ab ≥，且当a b ==时取等号．故33ab+≥≥，且当a b ==∴33a b +的最小值为(II)由(I)知，23a b +≥．由于6>，从而不存在,a b ，使得236a b +=．16．(2013全国I 文理)已知函数()f x =|21||2|x x a -++，()g x =3x +．(Ⅰ)当a =-2时，求不等式()f x ＜()g x 的解集；(Ⅱ)设a ＞-1，且当x ∈[2a -，12)时，()f x ≤()g x ，求a 的取值范围．【解析】(Ⅰ)当a =-2时，不等式()f x ＜()g x 化为|21||22|30x x x -+---<，设函数y =|21||22|3x x x -+---，y =15, 212, 1236, 1x x x x x x ⎧-<⎪⎪⎪--≤≤⎨⎪->⎪⎪⎩，其图像如图所示，从图像可知，当且仅当(0,2)x ∈时，y ＜0，∴原不等式解集是{|02}x x <<．(Ⅱ)当x ∈[2a -，12)时，()f x =1a +，不等式()f x ≤()g x 化为13a x ++≤，∴2x a -≥对x ∈[2a -，12)都成立，故2a -≥2a -，即a ≤43，∴a 的取值范围为(-1，43]．17．(2012新课标文理)已知函数|2|||)(-++=x a x x f ．(Ⅰ)当|3-=a 时，求不等式()3f x 的解集；(Ⅱ)若()|4|f x x - 的解集包含]2,1[，求a 的取值范围．【解析】(1)当3a =-时，()3323f x x x ⇔-+- 2323x x x ⎧⇔⎨-+-⎩ 或23323x x x <<⎧⇔⎨-+-⎩ 或3323x x x ⎧⇔⎨-+-⎩ 1x ⇔ 或4x ．(2)原命题()4f x x ⇔- 在[1,2]上恒成立24x a x x ⇔++-- 在[1,2]上恒成立22x a x ⇔--- 在[1,2]上恒成立30a ⇔- ．考点122不等式的证明18．(2020全国Ⅲ文理23)设,,,0,1a b c a b c abc ∈++==R ．(1)证明：0ab bc ca ++<；(2)用{}max ,,a b c 表示,,a b c 的最大值，证明：{}3max ,,4a b c ≥【答案】(1)证明见解析(2)证明见解析．【思路导引】(1)根据题设条件,0=++c b a 两边平方，再利用均值不等式证明即可；(2)思路一：不妨设max{,,}a b c a =，由题意得出0,,0a b c ><，由()222322b c b c bc a a a bc bc+++=⋅==，结合基本不等式，即可得出证明．思路二：假设出c b a ,,中最大值，根据反证法与基本不等式推出矛盾，即可得出结论．【解析】(1)证明：().0,02=++∴=++c b a c b a ,0222222=+++++∴ca ac ab c b a 即()222222c b a ca bc ab ++-=++.0,0222<++∴<++∴ca bc ab ca bc ab (2)证法一：不妨设max{,,}a b c a =，由0,1a b c abc ++==可知，0,0,0a b c ><<，1,a b c a bc =--= ，()222322224b c b c bc bc bc a a a bc bc bc++++∴=⋅==≥=，当且仅当b c =时，取等号，a ∴≥，即max{,,}a b c ．证法二：不妨设403<<<≤c b a ，则,4,41133>=-->=c b a c ab而1132a b ->--≥>==矛盾，∴命题得证．19．(2019全国I 文理23)已知a ，b ，c 为正数，且满足abc=1．证明：(1)222111a b c a b c++≤++；(2)333()()()24a b b c c a +++≥++．【解析】(1)因为2222222,2,2a b ab b c bc c a ac +≥+≥+≥，又1abc =，故有222111ab bc ca a b c ab bc ca abc a b c ++++≥++==++，∴222111a b c a b c++≤++．(2)因为, , a b c 为正数且1abc =，故有333()()()a b b c c a +++++≥=3(+)(+)(+)a b b c ac 3≥⨯⨯⨯=24．∴333()()()24a b b c c a +++++≥．20．(2019全国III 文理23)设,,x y z ∈R ，且1x y z ++=．(1)求222(1)(1)(1)x y z -++++的最小值；(2)若2221(2)(1)()3x y z a -+-+-≥成立，证明：3a ≤-或1a ≥-．【解析】(1)由于2[(1)(1)(1)]x y z -++++222(1)(1)(1)2[(1)(1)(1)(1)(1)(1)]x y z x y y z z x =-+++++-++++++-2223(1)(1)(1)x y z ⎡⎤≤-++++⎣⎦，故由已知得2224(1)(1)(1)3x y z -++++≥，当且仅当x=53，y=–13，13z =-时等号成立．∴222(1)(1)(1)x y z -++++的最小值为43．(2)由于2[(2)(1)()]x y z a -+-+-222(2)(1)()2[(2)(1)(1)()()(2)]x y z a x y y z a z a x =-+-+-+--+--+--2223(2)(1)()x y z a ⎡⎤-+-+-⎣⎦ ，故由已知2222(2)(2)(1)()3a x y z a +-+-+- ，当且仅当43a x -=，13a y -=，223a z -=时等号成立，因此222(2)(1)()x y z a -+-+-的最小值为2(2)3a +．由题设知2(2)133a + ，解得3a - 或1a - ．21．(2017全国Ⅱ文理)已知0a >，0b >，332a b +=，证明：(1)()()554a b a b ++≥；(2)2a b +≤．【解析】(1)556556()()a b a b a ab a b b ++=+++3323344()2()a b a b ab a b =+-++()22244ab a b =+-≥．(2)∵33223()33a b a a b ab b +=+++23()ab a b =++23()2()4a b a b +≤++33()24a b +=+，∴3()8a b +≤，因此2a b +≤．22．(2017江苏)已知a ，b ，c ，d 为实数，且224a b +=，2216c d +=，证明8ac bd +≤．【解析】证明：由柯西不等式可得：22222()()()ac bd a b c d +++≤，因为22224,16,a b c d +=+=∴2()64ac bd +≤，因此8ac bd +≤．23．(2016全国II 文理)已知函数()1122f x x x =-++，M 为不等式()2f x <的解集．(I)求M ；(II)证明：当a ，b M ∈时，1a b ab +<+．【解析】(I)当12x <-时，()11222f x x x x =---=-，若112x -<<-；当1122x -≤≤时，()111222f x x x =-++=<恒成立；当12x >时，()2f x x =，若()2f x <，112x <<．综上可得，{}|11M x x =-<<．(Ⅱ)当()11a b ∈-，，时，有()()22110a b -->，即22221a b a b +>+，则2222212a b ab a ab b +++>++，则()()221ab a b +>+，即1a b ab +<+，证毕．24．(2015全国II 文理)设,,,a b c d 均为正数，且a b c d +=+，证明：(Ⅰ)若ab >cd ，则a b c d +>+；(Ⅱ)a b c d +>+是||||a b c d -<-的充要条件．【解析】(Ⅰ)∵2()2a b a b ab +=++，2()c d c d cd +=++由题设a b c d +=+，ab cd >得22()a b c d >+a b c d +>(Ⅱ)(ⅰ)若||||a b c d -<-，则22()()a b c d -<-，即22()4()4a b ab c d cd +-<+-．因为a b c d +=+，∴ab cd >，由(Ⅰ)得a b c d >(ⅱ)a b c d +>则22(a b c d >+，即a b ab c d cd ++>++因为a b c d +=+，∴ab cd >，于是2222()()4()4()a b a b ab c d cd c d -=+-<+-=-．因此||||a b c d -<-．a b c d +>||||a b c d -<-的充要条件．25．(2013全国II 文理)设,,a b c 均为正数，且1a b c ++=，证明：(Ⅰ)13ab bc ca ++≤；(Ⅱ)2221a b c b c a++≥．【解析】(Ⅰ)2222222,2,2a b ab b c bc c a ca +≥+≥+≥得222a b c ab bc ca ++≥++，由题设得()21a b c ++=，即2222221a b c ab bc ca +++++=，∴()31ab bc ca ++≤，即13ab bc ca ++≤．(Ⅱ)∵2222,2,2a b c b a c b a c b c a +≥+≥+≥，∴222()2()a b c a b c a b c b c a +++++≥++，即222a b c a b c b c a ++≥++，∴2221a b c b c a ++≥．。

新高考数学《不等式选讲》练习题一、141．不等式的解集是 ( )A ．B ．C ．D ．【答案】B 【解析】 【分析】利用绝对值三角不等式，得到，恒成立.【详解】恒成立.故答案选B 【点睛】本题考查了解绝对值不等式，利用绝对值三角不等式简化了运算.2．设集合{}1,R A x x a x =-<∈，{}15,R B x x x =<<∈．若A B =∅I ，则实数a 的取值范围是（）A ．{}06a a ≤≤B ．{}64a a a ≤≥或C ．{}06a a a ≤≥或D ．{}24a a ≤≤【答案】C 【解析】 【分析】根据公式()0x a a a x a <>⇔-<<解出集合A ，再根据交集的运算即可列出关系式，求解即可。

【详解】由111x a x a -<⇔-<-<，解得11a x a -<<+，因为A B =∅I ， 所以11a +≤或15a -≥，解得0a ≤或6a ≥，即实数a 的取值范围是{}06a a a ≤≥或，故选：C. 【点睛】本题主要考查集合的交集运算应用以及绝对值不等式的解法。

3．已知()f x 是定义域为R 的偶函数，当0x …时，2()4f x x x =+，则(2)5f x +>的解集为（ ）A ．(,5)(5,)-∞-+∞UB ．(,5)(3,)-∞-+∞UC ．(,7)(3,)-∞-+∞UD ．(,7)(2,)-∞-+∞U【答案】C 【解析】 【分析】根据偶函数以及当0x …时，2()4f x x x =+,可得0x ≥时的表达式,由此求得(2)(|2|)f x f x +=+,再代入可解得.【详解】∵()f x 是定义域为R 的偶函数，∴当0x ≥时，0x -≤,所以22()()()4()4f x f x x x x x =-=-+-=-. 由()25f x +>以及()f x 为偶函数，得(|2|)5f x +>，∴2|2|4|2|5x x +-+>，所以(|2|5)(|2|1)0x x +-++>, 因为|2|10x ++>, 所以|2|5x +>,所以25x +>或25x +<-, 解得7<-x 或 3.x > 故选C 【点睛】本题考查了利用函数的奇偶性求函数解析式,绝对值不等式的解法,属于中档题.4．已知点(3,1)P 在椭圆22221(0)x y a b a b+=>>上，点(,)M a b 为平面上一点，O 为坐标原点，则当OM 取最小值时，椭圆的离心率为（ ）A ．3B ．13C ．2D ．3【答案】D 【解析】 【分析】点(3,1)P 在椭圆22221(0)x y a b a b +=>>上，可得22911a b +=，(,)M a b 为平面上一点，||OM =a ，b 关系，代入即可．【详解】解：点(3,1)P 在椭圆22221(0)x y a b a b+=>>上，可得22911a b +=，(,)M a b为平面上一点，||OM =所以||4OM ==，当且仅当223a b =时，取等号， 222213b e a =-=，e =． 故选D ． 【点睛】考查椭圆的性质，柯西不等式的应用，求椭圆的离心率，中档题．5．关于x 不等式2x x a a -+-≥在R 上恒成立，则实数a 的最大值是 A ．0 B ．1C ．－1D ．2【答案】B 【解析】由于|x －2|＋|x －a |≥|a －2|，∴等价于|a －2|≥a ，即a ≤1.故实数a 的最大值为1.6．2018年9月24日，英国数学家.M F 阿帝亚爵在“海德堡论坛”展示了他“证明”黎曼猜想的过程，引起数学界震动，黎曼猜想来源于一些特殊数列求和，记222111123S n =+++++L L ，则（ ） A ．413S << B ．4332S << C ．322S << D ．2S >【答案】C 【解析】 【分析】由题意，可知21111111(2,)1(1)(1)1n n N n n n n n n n n n+-=<<=-≥∈++--，利用放缩法和极限，即可得到答案. 【详解】 由题意，可知21111111(2,)1(1)(1)1n n N n n n n n n n n n+-=<<=-≥∈++--，所以2221111111113111()()()232334121n S n n n n =+++++>+-+-++-=-++L L L 22211111111111(1)()()2232231n S n n n nL L =++++<+-+-++-=--， 当n →+∞且n N +∈时，101n →+，且10n →，所以322S <<，故选C. 【点睛】本题主要考查了数列思想的应用问题，其中解答中，认真审题，利用21n 进行合理放缩，再利用极限求解是解答本题的关键，着重考查了分析问题和解答问题的能力，以及放缩思想的应用，属于中档试题.7．在平面内，已知向量(1,0)a =v，(0,1)b =v，(1,1)c =v，若非负实数,,x y z 满足1x y z ++=，且23p xa yb zc =++v v v v，则（ ）A ．p vB ．p v的最大值为C ．p vD ．p v的最大值为【答案】A 【解析】 【分析】求出p v 的坐标，表示p v ，即：p v柯西不等式即可求得其最小值，问题得解． 【详解】因为()1,0a =v ，()0,1b =v ，()1,1c=v， 所以23p xa yb zc =++v v v v=()3,23x z y z ++，又非负实数,,x y z 满足1x y z ++=，所以01z ≤≤，所以pv ==5≥==≥=， 当且仅当()()31232,0x z y z z +⨯=+⨯=时，等号成立． 即：当且仅当41,,055x y z ===时，等号成立．所以p v， 故选A. 【点睛】本题主要考查了柯西不等式的应用，还考查了向量的模及坐标运算，考查构造能力，属于中档题．8．已知各项均为正数的数列{}n a 的前n 项和为n S ，且()2*21221n n a a S n n N +==++∈，，若对任意的*n N ∈，1211120nn a n a n a λ++⋯+-≥+++恒成立，则实数λ的取值范围为（ ） A ．(]2∞-，B ．(]1∞-， C ．14∞⎛⎤- ⎥⎝⎦，D ．12，∞⎛⎤- ⎥⎝⎦【答案】C 【解析】 【分析】2212,21n n a a S n +==++ ()*n N ∈，可得2n ≥时，()221121210n n n n n n a a S S a a +--=-+=+>，．可得11n n a a +=+时，212224a a +==，解得1a ．利用等差数列的通项公式可得n a ．通过放缩即可得出实数λ的取值范围． 【详解】2212,21n n a a S n +==++Q ()*n N ∈，2n ∴≥时，()22112121n n n n n a a S S a +--=-+=+， 化为：222121(1)n n n n a a a a +=++=+，0n a >．11n n a a +∴=+，即11n n a a +-=，1n =时，212224a a +==，解得11a =．∴数列{}n a 为等差数列，首项为1，公差为1．11n a n n ∴=+-=． 1211111112n n a n a n a n n n n∴++⋯+=++⋯+++++++. 记11112n b n n n n =++⋯++++，1111111211n b n n n n +=++⋯++++++++. ()()11111022*******n n b b n n n n n +-=+-=>+++++.所以{}n b 为增数列，112n b b ≥=,即121111111122n n a n a n a n n n n ++⋯+=++⋯+≥++++++. Q 对任意的*n N ∈，1211120nn a n a n a λ++⋯+-≥+++恒成立， 122λ∴≤，解得14λ≤ ∴实数λ的取值范围为14∞⎛⎤- ⎥⎝⎦，．故选C ． 【点睛】本题考查了数列递推关系、等差数列的通项公式、放缩法，考查了推理能力与计算能力，属于中档题．9．已知函数()f x 是定义在[1,2]a a -上的偶函数,且当0x >时,()f x 单调递增，则关于x 的不等式(1)()f x f a ->的解集为 （ ） A ．45[,)33B ．2112(,][,)3333--⋃ C ．12[,)33⋃45(,]33D ．随a 的值而变化【答案】C 【解析】试题分析：∵函数()f x 是定义在[1,2]a a -上的偶函数，∴1-a=2a ，∴a=13，故函数()f x 的定义的定义域为22[,]33-，又当203x <≤时,()f x 单调递增，∴11113(1)()(1)(){23313x f x f f x f x ->->⇔->⇔-≤，解得1233x ≤<或4533x <≤，所以不等式(1)()f x f a ->的解集为12[,)33⋃45(,]33，故选C考点：本题考查了抽象函数的运用点评：此类问题往往利用偶函数的性质()()f x f x =避免了讨论，要注意灵活运用10．下列四个不等式：①log 10lg 2(1)x x x +>…；②a b a b -<+；③2(0)b a ab a b+≠…；④121x x -+-≥，其中恒成立的个数是( ) A ．1 B ．2C ．3D ．4【答案】C 【解析】 【分析】依次判断每个选项的正误，得到答案. 【详解】 ①1log 10lg lg 2(1)lg x x x x x+=+>…，当10x =时等号成立，正确 ②a b a b -<+，0b =时不成立，错误 ③，a b =时等号成立.正确④12(1)(2)1x x x x -+-≥---=，12x ≤≤时等号成立，正确 故答案选C 【点睛】本题考查了不等式性质，绝对值不等式，均值不等式，综合性较强，是不等式的常考题型.11．已知x+3y+5z=6,则x 2+y 2+z 2的最小值为( ) A ．65B ．6 35C ．36 35D ．6【答案】C 【解析】 【分析】由题意结合柯西不等式的结论求解x 2+y 2+z 2的最小值即可. 【详解】 由柯西不等式,得：x 2+y 2+z 2=(12+32+52)(x 2+y 2+z 22221)135++ ≥(1×x+3×y+5×z )2135⨯=26136.3535⨯= 当且仅当x 6186,,35357y z ===时等号成立. 即x 2+y 2+z 2的最小值为3635. 本题选择C 选项. 【点睛】根据题目特征，想到利用向量方法或利用柯西不等式想法比较自然.利用柯西不等式代数形式及其向量形式解题的方法是一致的.选择哪种方法进行解题，可能会因解题者的知识解构、思维特征及对问题与方法的熟悉程度做出选择.12．设x ∈R ，则“31x <”是“1122x -<”的( ) A ．充分而不必要条件 B ．必要而不充分条件 C ．充要条件 D ．既不充分也不必要条件【答案】B 【解析】 【分析】分别求解三次不等式和绝对值不等式确定x 的取值范围，然后考查充分性和必要性是否成立即可. 【详解】 由31x <可得1x <， 由1122x -<可得01x <<， 据此可知“31x <”是“1122x -<”的必要而不充分条件. 故选B . 【点睛】本题主要考查不等式的解法，充分性与必要性的判定等知识，意在考查学生的转化能力和计算求解能力.13．不等式222log 2log x x x x -<+的解集为（ ） A ．()1,2 B ．()0,1C ．()1,+∞D ．()2,+∞【答案】C 【解析】 【分析】由题意得出0x >，分2log 0x >和2log 0x ≤两种情况讨论，结合222log 2log x x x x -<+可得出2log 0x >，解出该不等式即可.【详解】由题意得出0x >，当2log 0x ≤时，则222log 2log x x x x -=+. 当2log 0x >时，222log 2log x x x x -<+，解不等式2log 0x >得1x >. 因此，不等式222log 2log x x x x -<+的解集为()1,+∞. 故选：C. 【点睛】本题考查绝对值不等式的求解，同时也考查绝对值三角不等式的应用，考查推理能力与运算求解能力，属于中等题.14．若,,a b c ∈R ，则下列结论中: (1)2211a a a a+≥+； (2)a b a c b c -≤-+-； (3)若a b >，则11a ba b>++；(4)若1a b +=，则2221a b a b +++的最小值为 其中正确结论的个数为( )A ．1B ．2C ．3D ．4【答案】B 【解析】 【分析】利用函数知识、换元法、绝对值不等式等知识，对选项进行一一推理证明，即可得答案. 【详解】 对（1），2221111()()20a a a a a a a a +≥+⇔+-+-≥，∴12a a +≥或11a a+≤-， ∵12a a +≥或12a a+≤-，∴原不等式成立，故（1）正确；对（2），∵()()a b a c b c a c b c -=---≤-+-，故（2）正确； 对（3），令1,52a b =-=-，则51,114a b a b =-=++，显然11a b a b>++不成立，故（3）错误；对（4），∵1a b +=，∴222222(1)231111a b b b b a b b b b+-+++=+=+-+-，当1b >时，2301b b+<-，∴2221a b a b +++的最小值为4）错误. 故选：B. 【点睛】本题考查函数与不等式的知识，考查函数与方程思想、转化与化归思想，考查逻辑推理能力和运算求解能力，求解时注意消元法、换元法的使用.15．设x,y,z 是互不相等的正数，则下列不等式中不恒成立的是（ ）A ．2211x x x x++≥ BC ．12x y x y-+≥- D ．x y x z y z -≤-+- 【答案】C 【解析】 【分析】 【详解】试题分析：x y x z z y x z z y x z y z -=-+-≤-+-=-+-，故D 恒成立； 由于函数()1f x x x=+,在(]0,1单调递减；在[)1,+∞单调递增, 当1x >时, ()()221,x x f x f x >>>即2211x x x x+>+,当01x <<,()()2201,x x f x f x <<即2211x x x x++≥正确，即A 正确；=<=,故B 恒成立，若1x y -=-,不等式12x y x y-+≥-不成立, 故C 不恒成立,故选C ． 考点：1、基本不等式证明不等式；2、单调性证明不等式及放缩法证明不等式．16．已知三个正实数a 、b 、c 满足1a b c ++=，给出以下几个结论：①22213a b c ++≤；②13ab bc ca ++≤；③2221b c a a b c++≥；≥.则正确的结论个数为( ) A ．1 B ．2C ．3D ．4【答案】B 【解析】 【分析】利用基本不等式及柯西不等式计算可得； 【详解】解：①：Q 222222222a b ab b c bc a c ac ⎧+⎪+⎨⎪+⎩………，222a b c ab bc ac ∴++++… 2222222()2223()a b c a b c ab ac bc a b c ∴++=+++++++„．22213a b c ∴++…，故①不正确．②：由2222()2()3()a b c a b c ab bc ac ab bc ac ++=+++++++…，13ab bc ca ∴++„，故②正确．③：Q 222222b a b ac b c b a c c c ⎧+⎪⎪⎪+⎨⎪⎪+⎪⎩………，∴2221b c aa b c a b c ++++=… ∴2221b c a a b c++…，故③正确． ④：由柯西不等式得2()(111)a b c ++++，∴≤．则④错误．故选：B ． 【点睛】本题考查利用基本不等式即柯西不等式证明不等式，属于中档题．17．函数()f x cosx = ，则()f x 的最大值是（ ） ABC ．1D ．2【答案】A 【解析】 【分析】将()f x 化为()f x cosx =，利用柯西不等式即可得出答案.【详解】因为()f x cosx = 所以()f x cosx=„=当且仅当cosx =. 故选：A 【点睛】本题主要考查了求函数的最值，涉及了柯西不等式的应用，属于中档题.18．定义在R 上的偶函数()y f x =在[)0,+∞上递减，且()10f =，则满足12log 0f x ⎛⎫< ⎪⎝⎭的x 的取值范围是( ) A ．()10,2,2⎛⎫+∞ ⎪⎝⎭U B ．()1,11,22⎛⎫⎪⎝⎭U C ．()1,2,2⎛⎫-∞+∞ ⎪⎝⎭U D ．()1,12,2⎛⎫⋃+∞ ⎪⎝⎭【答案】A 【解析】 【分析】利用函数()f x 的奇偶性和单调性化简不等式12log 0f x ⎛⎫< ⎪⎝⎭，得到12log 1x >，解绝对值不等式和对数不等式，求得x 的取值范围. 【详解】偶函数()y f x =在[)0,+∞上递减，且()10f =，所以()y f x =在(),0-∞上递增，且()10f -=，且距离对称轴越远，函数值越小，由12log 0f x ⎛⎫< ⎪⎝⎭可得12log 1x >，所以12log 1x >或12log 1x <-，解可得，102x <<或2x >. 故选：A. 【点睛】本小题主要考查利用函数的奇偶性的单调性解抽象函数不等式，考查绝对值不等式、对数不等式的解法，属于中档题.19．已知函数()222,2log 1,2x x x f x x x ⎧-+≤=⎨->⎩，设12116n x x x ≤<<<≤L ，若()()()()()()12231n n f x f x f x f x f x f x M --+-++-≤L ，则M 的最小值为( )A ．3B ．4C ．5D ．6【答案】B 【解析】 【分析】作出函数的图象，由已知分段函数求得f （1）1=，f （2）0=，(16)3f =，等价于12231max [|()()||()()||()()|]n n M f x f x f x f x f x f x -∴≥-+-+⋯+-，再求出不等式右边的最大值即可得M 的最小值．由222,2()log 1,2x x x f x x x ⎧-+=⎨->⎩„，得f （1）1=，f （2）0=，(16)3f =．12116n x x x <<⋯<Q 剟，12231|()()||()()||()()|n n M f x f x f x f x f x f x -∴-+-+⋯+-… 12231max[|()()||()()||()()|]n n M f x f x f x f x f x f x -∴≥-+-+⋯+-12231|()()||()()||()()||(1)(2)||(2)(16)=|10||30|4n n f x f x f x f x f x f x f f f f --+-+⋯+-≤-+--+-=∴4M ≥． 则M 的最小值为4． 故选：B ． 【点睛】本题考查分段函数及其应用，考查三角绝对值不等式的应用，意在考查学生对这些知识的理解掌握水平．20．已知,,x y z R +∈,且1x y z ++=，则222x y z ++的最小值是（ ） A ．1 B ．13C ．12D ．3【答案】B 【解析】 【分析】利用柯西不等式得出()()()2222222111xy z x y z ++++≥++，于此可得出222x y z ++【详解】由柯西不等式得()()()2222222211111xy z x y z ++++≥++==，则22213x y z ++≥，当且仅当13x y z ===时，等号成立，因此，222x y z ++的最小值为13，故选：B.【点睛】本题考查利用柯西不等式求最值，关键在于对代数式朝着定值条件等式去进行配凑，同时也要注意等号成立的条件，属于中等题。

历年（2014-2023）全国高考数学真题分项（不等式选讲）好题汇编题型一：含绝对值不等式的解法1．(2021年高考全国乙卷理科·第23题)已知函数()3f x x a x =-++．(1)当1a =时，求不等式()6f x ≥的解集; (2)若()f x a >-，求a 的取值范围．2．(2020年高考课标Ⅱ卷理科·第23题)已知函数2()|21|f x x a x a =-+-+．(1)当2a =时，求不等式()4f x …的解集；(2)若()4f x …，求a 的取值范围．3．(2020江苏高考·第23题)设x ∈R ，解不等式2|1|||4x x ++≤． 4．(2019·全国Ⅱ·理·第23题)已知函数()()2f x x a x x x a =-+--．()1当1a =时，求不等式()0f x <的解集；()2当(),1x ∈-∞时，()0f x <，求a 的取值范围．5．(2019·江苏·第23题)设x ∈R ，解不等式||+|2 1|>2x x -.6．(2015高考数学新课标1理科·第24题)(本小题满分10分)选修4—5：不等式选讲已知函数()12,0f x x x a a =+-->． (Ⅰ)当1a =时，求不等式()1f x >的解集；(Ⅱ)若()f x 的图像与x 轴围成的三角形面积大于6，求a 的取值范围7．(2015高考数学江苏文理·第24题)解不等式|23|2x x ++≥8．(2014高考数学课标2理科·第24题)(本小题满分10)选修4-5：不等式选讲．设函数()f x =1(0)x x a a a++->(Ⅰ)证明：()f x ≥2；(Ⅱ)若()35f <，求a 的取值范围．9．(2017年高考数学新课标Ⅰ卷理科·第23题)[选修4—5:不等式选讲]已知函数,．()24f x x ax =-++()11g x x x =++-(1)当时,求不等式的解集;(2)若不等式的解集包含,求的取值范围10．(2017年高考数学课标Ⅲ卷理科·第23题)[选修4—5：不等式选讲](10分)已知函数． (1)求不等式的解集；(2)若不等式的解集非空，求的取值范围．11．(2016高考数学课标Ⅲ卷理科·第24题)选修4—5:不等式选讲已知函数()2f x x a a =-+.(Ⅰ)当2a =时,求不等式()6f x ≤的解集;(Ⅱ)设函数()21g x x =-,当R x ∈时,()()3f x g x +≥,求a 的取值范围.题型二：不等式的最值1．(2018年高考数学江苏卷·第24题)[选修4—5：不等式选讲](本小题满分10分)若x ，y ，z 为实数，且x +2y +2z =6，求222x y z ++的最小值． 2．(2014高考数学课标1理科·第24题)选修4—5:不等式选讲若,且． (1)求的最小值;(2)是否存在,使得?并说明理由．3．(2015高考数学陕西理科·第24题)(本小题满分10分)选修4-5：不等式选讲已知关于x 的不等式x a b +<的解集为{}24x x <<． (Ⅰ)求实数a ，b 的值；的最大值．4．(2015高考数学福建理科·第23题)选修4-5：不等式选讲已知0,0,0a b c >>>，函数()||||f x x a x b c =++-+的最小值为4．(Ⅰ)求a b c ++的值； (Ⅱ)求2221149a b c ++的最小值． 题型三：含绝对值不等式的成立问题1．(2018年高考数学课标Ⅱ卷(理)·第23题)[选修4－5：不等式选讲](10分)1a =()()f x g x ≥()()f x g x ≥[]1,1-a ()12f x x x =+--()1f x ≥()2f x x x m ≥-+m 0,0a b >>11a b+=33a b +,a b 236a b +=设函数()5|||2|f x x a x =-+--． (1)当1a =时，求不等式()0f x ≥的解集； (2)若()1f x ≤，求a 的取值范围．2．(2018年高考数学课标卷Ⅰ(理)·第23题)[选修4–5：不等式选讲](10分)已知()|1||1|f x x ax =+--．(1)当1a =时，求不等式()1f x >的解集；(2)若(0,1)x ∈时不等式()f x x >成立，求a 的取值范围．题型四：含绝对值函数的图像及其应用1．(2023年全国甲卷理科·第23题)设0a >，函数()2f x x a a =--．(1)求不等式()f x x <的解集；(2)若曲线()y f x =与x 轴所围成的图形的面积为2，求a ．2．(2023年全国乙卷理科·第23题)已知()22f x x x =+-．(1)求不等式()6f x x ≤-的解集； (2)在直角坐标系xOy 中，求不等式组()60f x yx y ≤⎧⎨+-≤⎩所确定的平面区域的面积．3．(2020年高考课标Ⅰ卷理科·第23题)已知函数()|31|2|1|f x x x =+--．(1)画出()y f x =的图像；(2)求不等式()(1)f x f x >+的解集．4．(2016高考数学课标Ⅰ卷理科·第24题)(本小题满分10分)选修4—5：不等式选讲已知函数(x)123f x x =+--． (I )画出(x)y f =的图像；(II )求不等式(x)1f ൐的解集．(I )见解析 (II )()()11353⎛⎫-∞+∞ ⎪⎝⎭，，，5．(2018年高考数学课标Ⅲ卷(理)·第23题)【选修4—5：不等式选讲】(10分)设函数()211f x x x =++-． (1)画出()y f x =的图象；(2)当[)0,x ∈+∞时，()f x ax b ≤+，求a b +的最小值．题型五：不等式证明1．(2017年高考数学江苏文理科·第24题)[选修4-5:不等式选讲]已知为实数,且证明2．(2022年高考全国甲卷数学(理)·第23题)已知a ，b ，c 均为正数，且22243a b c ++=，证明：(1)23a b c ++≤； (2)若2b c =，则113a c+≥． 3．(2020年高考课标Ⅲ卷理科·第23题)设a ，b ，c ∈R ，a +b +c =0，abc =1．(1)证明：ab +bc +ca <0；(2)用max{a ，b ，c }表示a ，b ，c 中的最大值，证明：max{a ，b ，c．,,,a b c d 22224,16,a b c d +=+=8.ac bd +≤4．(2019·全国Ⅲ·理·第23题)设,,x y z R ∈，且1x y z ++=．(1)求222(1)(1)(1)x y z -++++的最小值；(2)若2221(2)(1)()3x y z a -+-+-≥成立，证明：3a -≤或1a -≥． 5．(2019·全国Ⅰ·理·第23题)已知a ，b ，c 为正数，且满足1abc =．证明：(1)222111a b c a b c++++≤； (2)333()()()24a b b c c a +++++≥．6．(2014高考数学辽宁理科·第24题)(本小题满分10分)选修4-5：不等式选讲设函数()2|1|1f x x x =-+-，2()1681g x x x =-+，记()1f x ≤的解集为M ，()4g x ≤的解集为N ． (1)求M ；(2)当x M N ∈ 时，证明：221()[()]4x f x x f x +≤． 7．(2014高考数学江苏·第24题)【选修4 - 5：不等式选讲】已知0,0x y >>，证明：22(1)(1)9x y x y xy ++++≥．8．(2014高考数学福建理科·第23题)(本小题满分7分)选修4—5：不等式选讲已知定义在R 上的函数21)(+++=x x x f 的最小值为a ． (I )求a 的值；(II )若r q p ,,为正实数，且a r q p =++，求证：3222≥++r q p ．9．(2015高考数学新课标2理科·第24题)(本小题满分10分)选修4-5不等式选讲设,,,a b c d 均为正数，且a b c d +=+，证明：(Ⅰ)若ab cd >>+>是a b c d -<-的充要条件．10．(2015高考数学湖南理科·第18题)设0,0a b >>，且11a b a b+=+．证明: (1)2a b +≥；(2)22a a +<与22b b +<不可能同时成立．11．(2017年高考数学课标Ⅱ卷理科·第23题)[选修4-5：不等式选讲](10分)已知，证明：(1)；(2)．12．(2016高考数学课标Ⅱ卷理科·第24题)(本小题满分10分)选修4—5：不等式选讲已知函数()1122f x x x =-++，M 为不等式()2f x <的解集． (I )求M ；(II )证明：当,a b M ∈时，1a b ab +<+．330,0,2a b a b >>+=33()()4a b a b ++≥2a b +≤13．(2016高考数学江苏文理科·第24题)[选修4-5：不等式选讲]设0a >，13a x -<，23ay -<，求证：24x y a +-<．参考答案题型一：含绝对值不等式的解法1．(2021年高考全国乙卷理科·第23题)已知函数()3f x x a x =-++．(1)当1a =时，求不等式()6f x ≥的解集; (2)若()f x a >-，求a 的取值范围． 【答案】(1)(][),42,-∞-+∞ ．(2)3,2⎛⎫-+∞ ⎪⎝⎭． 答案解析：(1)当1a =时，()13f x x x =-++，13x x -++表示数轴上的点到1和3-的距离之和， 则()6f x ≥表示数轴上的点到1和3-的距离之和不小于6，故4x ≤-或2x ≥， 所以()6f x ≥的解集为(][),42,-∞-+∞ ．(2)依题意()f x a >-，即3a x a x -+>-+恒成立，333x a x x a a x -++-+=≥++，故3a a +>-，所以3a a +>-或3a a +<， 解得32a >-． 所以a 的取值范围是3,2⎛⎫-+∞ ⎪⎝⎭． 【点睛】解绝对值不等式的方法有零点分段法、几何意义法．2．(2020年高考课标Ⅱ卷理科·第23题)已知函数2()|21|f x x a x a =-+-+．(1)当2a =时，求不等式()4f x …的解集；(2)若()4f x …，求a 的取值范围．【答案】(1)32x x ⎧≤⎨⎩或112x ⎫≥⎬⎭；(2)(][),13,-∞-+∞ ．答案解析：(1)当2a =时，()43f x x x =-+-． 当3x ≤时，()43724f x x x x =-+-=-≥，解得：32x ≤； 当34x <<时，()4314f x x x =-+-=≥，无解； 当4x ≥时，()43274f x x x x =-+-=-≥，解得：112x ≥； 综上所述：()4f x ≥的解集为32x x ⎧≤⎨⎩或112x ⎫≥⎬⎭． (2)()()()()22222121211f x x a x a x ax a a a a =-+-+≥---+=-+-=-(当且仅当221a x a -≤≤时取等号)，()214a ∴-≥，解得：1a ≤-或3a ≥，a ∴的取值范围为(][),13,-∞-+∞ ．【点睛】本题考查绝对值不等式的求解、利用绝对值三角不等式求解最值的问题，属于常考题型． 3．(2020江苏高考·第23题)设x ∈R ，解不等式2|1|||4x x ++≤．【答案】22,3⎡⎤-⎢⎥⎣⎦【答案解析】1224x x x <-⎧⎨---≤⎩ 或10224x x x -≤≤⎧⎨+-≤⎩或0224x x x >⎧⎨++≤⎩21x ∴-≤<-或10x -≤≤或203x <≤,所以解集为22,3⎡⎤-⎢⎥⎣⎦4．(2019·全国Ⅱ·理·第23题)已知函数()()2f x x a x x x a =-+--．()1当1a =时，求不等式()0f x <的解集；()2当(),1x ∈-∞时，()0f x <，求a 的取值范围． 【答案】()1(),1-∞；()2[)1,+∞【官方答案解析】()1当1a =时，()=|1| +|2|(1)f x x x x x ---.当1x <时，2()2(1)0f x x =--<；当1x ≥时，()0f x ≥. 所以，不等式()0f x <的解集为(,1)-∞.()2因为()=0f a ，所以1a ≥.当1a ≥，(,1)x ∈-∞时，()=() +(2)()=2()(1)<0f x a x x x x a a x x ----- 所以，a 的取值范围是[1,)+∞.【分析】()1根据1a =，将原不等式化为()1210x x x x -+--<，分别讨论1x <，12x <≤，2x ≥三种情况，即可求出结果；()2分别讨论1a ≥和1a <两种情况，即可得出结果.【答案解析】()1当1a =时，原不等式可化为()1210x x x x -+--<；当1x <时，原不等式可化，即()210x ->，显然成立， 此时解集为(),1-∞；当12x <≤时，原不等式可化为()()()1210x x x x -+--<，解得1x <，此时解集为空集； 当2x ≥时，原不等式可化为()()()1210x x x x -+--<，即()210x -<，显然不成立；此时解集为空集；综上，原不等式的解集为(),1-∞；()2当1a ≥时，因为(),1x ∈-∞，所以由()0f x <可得()()()20a x x x x a -+--<，即()()10x a x -->，显然恒成立；所以1a ≥满足题意；当1a <时，()()()2,1()21,x a a x f x x a x x a -<⎧⎪=⎨--<⎪⎩≤，因1a x <≤时， ()0f x <显然不能成立，所以1a <不满足题意；综上，a 的取值范围是[)1,+∞.【点评】本题主要考查含绝对值的不等式，熟记分类讨论的方法求解即可，属于常考题型.5．(2019·江苏·第23题)设x ∈R ，解不等式||+|2 1|>2x x -.【答案】见答案解析【答案解析】当0x <时，原不等式可化为122x x -+->，解得13x <-；当12x 0≤≤时，原不等式可化为122x x +->，即1x <-，无解；当12x >时，原不等式可化为212x x +->，解得1x >. 综上，原不等式的解集为1{|1}3x x x <->或.6．(2015高考数学新课标1理科·第24题)(本小题满分10分)选修4—5：不等式选讲已知函数()12,0f x x x a a =+-->．为为(Ⅰ)当1a =时，求不等式()1f x >的解集；(Ⅱ)若()f x 的图像与x 轴围成的三角形面积大于6，求a 的取值范围 【答案】(Ⅰ)2{|2}3x x <<(Ⅱ)(2，+∞) 分析：(Ⅰ)利用零点分析法将不等式f (x )>1化为一元一次不等式组来解；(Ⅱ)将()f x 化为分段函数，求出()f x 与x 轴围成三角形的顶点坐标，即可求出三角形的面积，根据题意列出关于a 的不等式，即可解出a 的取值范围．答案解析：(Ⅰ)当a =1时，不等式f (x )>1化为|x +1|-2|x -1|＞1，等价于11221x x x ≤-⎧⎨--+->⎩或111221x x x -<<⎧⎨++->⎩或11221x x x ≥⎧⎨+-+>⎩，解得223x <<， 所以不等式f (x )>1的解集为2{|2}3x x <<．(Ⅱ)由题设可得，12,1()312,112,x a x f x x a x a x a x a --<-⎧⎪=+--≤≤⎨⎪-++>⎩，所以函数()f x 的图像与x 轴围成的三角形的三个顶点分别为21(,0)3a A -，(21,0)B a +，(,+1)C a a ，所以△ABC 的面积为22(1)3a +． 由题设得22(1)3a +＞6，解得2a >． 所以a 的取值范围为(2，+∞)．7．(2015高考数学江苏文理·第24题)解不等式|23|2x x ++≥【答案】153x x x ⎧⎫≤-≥-⎨⎬⎩⎭或分析：根据绝对值定义将不等式化为两个不等式组的并集，分别求解即可答案解析：原不等式可化为3232x x ⎧<-⎪⎨⎪--≥⎩或32332x x ⎧≥-⎪⎨⎪+≥⎩．解得5x ≤-或13x ≥-．综上，原不等式的解集是153x x x ⎧⎫≤-≥-⎨⎬⎩⎭或．8．(2014高考数学课标2理科·第24题)(本小题满分10)选修4-5：不等式选讲．设函数()f x =1(0)x x a a a++->(Ⅰ)证明：()f x ≥2；(Ⅱ)若()35f <，求a 的取值范围．【答案】答案解析：(Ⅰ)11112x x a x a x x a x a a a a a++-=++-≥++-=+≥，仅当1a =时等号成立，所以()f x ≥2．(Ⅱ)()3f =1133335a a a a++-=-++<当03a <<时，()3f =165a a -+<，解得12a +>当3a ≥时，()3f =15a a +<，解得52a +>综上所述，a的取值范围为15(,22++．9．(2017年高考数学新课标Ⅰ卷理科·第23题)[选修4—5:不等式选讲]已知函数,．(1)当时,求不等式的解集;(2)若不等式的解集包含,求的取值范围【答案】(1);(2)．【分析】(1)将代入,不等式等价于,对按,,讨论,得出最值的解集;(2)当时,．若的解集包含,等价于当时,,则在的最小值必为与之一,所以且,得,所以的取值范围为．【答案解析】(1)当时,不等式等价于①当时,①式化为,无解;当时,①式化为,从而;当时,①式化为,从而 所以不等式的解集为(2)当时,所以的解集包含,等价于当时,又在的最小值必为与之一,所以,得． 所以的取值范围为．10．(2017年高考数学课标Ⅲ卷理科·第23题)[选修4—5：不等式选讲](10分)已知函数．()24f x x ax =-++()11g x x x =++-1a =()()f x g x ≥()()f x g x ≥[]1,1-a 112x x ⎧-+⎪-≤≤⎨⎪⎪⎩⎭[]1,1-1a =()()f x g x ≥2|1||1|40x x x x -+++--≤x 1x <-11x -≤≤1x >[1,1]x ∈-()2g x =()()f x g x ≥[1,1]-[]1,1x ∈-()2f x ≥()f x []1,1-()1f -()1f ()12f -≥()12f ≥11a -≤≤a []1,1-1a =()()f x g x ≥21140x x x x -+++--<1x <-2340x x --≤11x -≤≤220x x --≤11x -≤≤1x >240x x +-≤112x -<≤()()f x g x≥112xx ⎧-+⎪-≤≤⎨⎪⎪⎩⎭[]1,1x ∈-()2g x =()()f x g x ≥[]1,1-[]1,1x ∈-()2f x ≥()f x []1,1-()1f -()1f ()()1212f f -≥⎧⎪⎨≥⎪⎩11a -≤≤a []1,1-()12f x x x =+--(1)求不等式的解集；(2)若不等式的解集非空，求的取值范围．【答案】(Ⅰ);(Ⅱ)【答案解析】(1)因为所以不等式等价于或或由无解；由；由 综上可得不等式的解集为．(2)解法一：先求不等式的解集为空集时的取值范围不等式的解集为空集等价于不等式恒成立记，则当时， 当时，当时， 所以 所以不等式的解集为空集时， 所以不等式的解集非空时，的取值范围为．解法二：原式等价于存在，使成立，即设()1f x ≥()2f x x x m ≥-+m {}1x x ≥5-，4⎛⎤∞ ⎥⎝⎦()3, 11221, 123, 2x f x x x x x x -<-⎧⎪=+--=-≤≤⎨⎪>⎩()1f x ≥131x <-⎧⎨-≥⎩12211x x -≤≤⎧⎨-≥⎩231x >⎧⎨≥⎩131x <-⎧⎨-≥⎩⇒x 1222x x -≤≤⎧⎨≥⎩12x ⇒≤≤231x >⎧⎨≥⎩2x ⇒≥()1f x ≥[)1,+∞()2f x x x m ≥-+m ()2f x x x m ≥-+()2m f x x x >-+()()2F x f x x x =-+2223, 131, 123, 2x x x x x x x x x ⎧-+-<-⎪-+-≤≤⎨⎪-++>⎩()max m F x >⎡⎤⎣⎦1x <-()()2211131524F x x x x F ⎛⎫=-+-=---<-=- ⎪⎝⎭12x -≤≤()223535312424F x x x x F ⎛⎫⎛⎫=-+-=--+≤= ⎪ ⎪⎝⎭⎝⎭2x >()()2211332124F x x x x F ⎛⎫=-++=--+<= ⎪⎝⎭()max 3524F x F ⎛⎫==⎡⎤⎪⎣⎦⎝⎭()2f x x x m ≥-+54m >()2f x x x m ≥-+m 5,4⎛⎤-∞ ⎥⎝⎦x R ∈2()f x x x m -+≥2max [()]f x x x m -+≥2()()g x f x x x =-+由(1)知当时，，其开口向下，对称轴 所以当时，，其开口向下，对称轴为 所以 当时，，其开口向下，对称轴为 所以 综上 所以的取值范围为．11．(2016高考数学课标Ⅲ卷理科·第24题)选修4—5:不等式选讲已知函数()2f x x a a =-+.(Ⅰ)当2a =时,求不等式()6f x ≤的解集;(Ⅱ)设函数()21g x x =-,当R x ∈时,()()3f x g x +≥,求a 的取值范围. 【答案】(Ⅰ){}13x x -≤≤;(Ⅱ)[)2,+∞.【答案解析】(Ⅰ)当2a =时,()222f x x =-+.解不等式2226x -+≤,得13x -≤≤.因此,()6f x ≤的解集为{}13x x -≤≤. (Ⅱ)当R x ∈时,()()2122121f x g x x a a x x a x a a a +=-++--+-+=-+≥ 当12x =时等号成立. 所以当R x ∈时,()()3f x g x +≥等价于13a a -+≥.① 当1a ≤时,①等价于13a a -+≥,无解. 当1a >时,①等价于13a a -+≥,解得2a ≥2223,1()31,123,2x x x g x x x x x x x ⎧-+-≤-⎪=-+--<<⎨⎪-++≥⎩1x ≤-2()3g x x x =-+-112x =>-()()11135g x g ≤-=---=-12x -<<()231g x x x =-+-32x =()399512424g x g ⎛⎫≤=-+-= ⎪⎝⎭2x ≥()23g x x x =-++12x =()()24231g x g ≤=-++=()max 54g x =⎡⎤⎣⎦m 5,4⎛⎤-∞ ⎥⎝⎦所以的取值范围是[)2,+∞.题型二：不等式的最值1．(2018年高考数学江苏卷·第24题)[选修4—5：不等式选讲](本小题满分10分)若x ，y ，z 为实数，且x +2y +2z =6，求222x y z ++的最小值． 【答案】4证明：由柯西不等式，得2222222()(122)(22)x y z x y z ++++≥++． 因为22=6x y z ++，所以2224x y z ++≥， 当且仅当122x y z ==时，不等式取等号，此时244333x y z ===，，，所以222x y z ++的最小值为4．2．(2014高考数学课标1理科·第24题)选修4—5:不等式选讲若,且． (1)求的最小值;(2)是否存在,使得?并说明理由． 【答案】答案解析:(1,得,且当时等号成立,故,且当∴的最小值为．(2)由,得,又由(1)知,二者矛盾, 所以不存在,使得成立．3．(2015高考数学陕西理科·第24题)(本小题满分10分)选修4-5：不等式选讲已知关于x 的不等式x a b +<的解集为{}24x x <<． (Ⅰ)求实数a ，b 的值；的最大值．【答案】(Ⅰ)3a =-，1b =；(Ⅱ)4．分析：(Ⅰ)先由x a b +<可得b a x b a --<<-，再利用关于x 的不等式x a b +<的解集为{}24x x <<可得a ，b +变形为，再利用柯西不等式的最大值．答案解析：(Ⅰ)由||x a b +<，得b a x b a --<<- 则2,4,b a b a --=⎧⎨-=⎩解得3a =-,1b =0,0a b >>11a b+=33a b +,a b 236a b +=11a b =+?2ab ³a b ==33a b +?a b =33a b +623a b =+?32ab £2ab ³,a b 236a b +==≤4==1=，即1t=时等号成立，故max4=．4．(2015高考数学福建理科·第23题)选修4-5：不等式选讲已知0,0,0a b c>>>，函数()||||f x x a x b c=++-+的最小值为4．(Ⅰ)求a b c++的值；(Ⅱ)求2221149a b c++的最小值．【答案】(Ⅰ)4；(Ⅱ)87．答案解析：(Ⅰ)因为(x)|x||x||(x)(x)||a|f a b c a b c b c=++++?-++=++，当且仅当a x b-＃时，等号成立，又0,0a b>>，所以|a b|a b+=+,所以(x)f的最小值为a b c++, 所以a b c4++=．(Ⅱ)由(1)知a b c4++=，由柯西不等式得()()22222114912+3+1164923a ba b c c a b c⎛⎫⎛⎫++++≥⨯⨯⨯=++=⎪ ⎪⎝⎭⎝⎭,即222118497a b c++?．当且仅当1132231ba c==,即8182,,777a b c===时，等号成立所以2221149a b c++的最小值为87．题型三：含绝对值不等式的成立问题1．(2018年高考数学课标Ⅱ卷(理)·第23题)[选修4－5：不等式选讲](10分)设函数()5|||2|f x x a x=-+--．(1)当1a=时，求不等式()0f x≥的解集；(2)若()1f x≤，求a的取值范围．【答案】答案解析：(1)当1a=时，24,1,()2,12,26, 2.x xf x xx x+-⎧⎪=-<⎨⎪-+>⎩≤≤可得()0≥f x的解集为{}|23≤≤x x-．(2)()1f x≤等价于|||2|4≥x a x++-．而|||2||2|≥x a x a ++-+，且当2x =时等号成立，故()1f x ≤等价于|2|4≥a +． 由|2|4≥a +可得6≤a -或2≥a ，所以a 的取值范围是(][),62,-∞-+∞ ． 2．(2018年高考数学课标卷Ⅰ(理)·第23题)[选修4–5：不等式选讲](10分)已知()|1||1|f x x ax =+--．(1)当1a =时，求不等式()1f x >的解集；(2)若(0,1)x ∈时不等式()f x x >成立，求a 的取值范围．【答案】答案解析：(1)当1a =时，()|1||1|f x x x =+--，即2,1,()2,11,2, 1.x f x x x x -≤-⎧⎪=-<<⎨⎪≥⎩故不等式()1f x >的解集为1{|}2x x >．(2)当(0,1)x ∈时|1||1|x ax x +-->成立等价于当(0,1)x ∈时|1|1ax -<成立． 若0a ≤，则当(0,1)x ∈时|1|1ax -≥； 若0a >，|1|1ax -<的解集为20x a <<，所以21a≥，故02a <≤． 综上，a 的取值范围为(0,2]．题型四：含绝对值函数的图像及其应用1．(2023年全国甲卷理科·第23题)设0a >，函数()2f x x a a =--．(1)求不等式()f x x <的解集；(2)若曲线()y f x =与x 轴所围成的图形的面积为2，求a ． 【答案】(1),33a a ⎛⎫⎪⎝⎭(2)2答案解析：(1)若x a ≤,则()22f x a x a x =--<, 即3x a >,解得3a x >,即3ax a <≤, 若x a >,则()22f x x a a x =--<, 解得3x a <,即3a x a <<, 综上,不等式的解集为,33a a ⎛⎫⎪⎝⎭．(2)2,()23,x a x a f x x a x a -+≤⎧=⎨->⎩． 画出()f x 的草图,则()f x 与x 轴围成ABC ,ABC 的高为3,,0,,022a a a A B ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭,所以||=AB a ,所以211||222ABC S AB a a =⋅== ,解得2a =．2．(2023年全国乙卷理科·第23题)已知()22f x x x =+-．(1)求不等式()6f x x ≤-的解集；(2)在直角坐标系xOy 中，求不等式组()60f x yx y ≤⎧⎨+-≤⎩所确定的平面区域的面积． 【答案】(1)[2,2]-； (2)8．答案解析：(1)依题意，32,2()2,0232,0x x f x x x x x ->⎧⎪=+≤≤⎨⎪-+<⎩，不等式()6f x x ≤-化为：2326x x x >⎧⎨-≤-⎩或0226x x x ≤≤⎧⎨+≤-⎩或0326x x x <⎧⎨-+≤-⎩， 解2326x x x >⎧⎨-≤-⎩，得无解；解0226x x x ≤≤⎧⎨+≤-⎩，得02x ≤≤，解0326x x x <⎧⎨-+≤-⎩，得20x -≤<，因此22x -≤≤，所以原不等式的解集为：[2,2]-(2)作出不等式组()60f x yx y ≤⎧⎨+-≤⎩表示的平面区域，如图中阴影ABC ，由326y x x y =-+⎧⎨+=⎩，解得(2,8)A -，由26y x x y =+⎧⎨+=⎩, 解得(2,4)C ，又(0,2),(0,6)B D ， 所以ABC 的面积11|||62||2(2)|822ABC C A S BD x x =⨯-=-⨯--= ． 3．(2020年高考课标Ⅰ卷理科·第23题)已知函数()|31|2|1|f x x x =+--．(1)画出()y f x =的图像；(2)求不等式()(1)f x f x >+的解集． 【答案】(1)详解答案解析；(2)7,6⎛⎫-∞-⎪⎝⎭． 【答案解析】(1)因为()3,1151,1313,3x x f x x x x x ⎧⎪+≥⎪⎪=--<<⎨⎪⎪--≤-⎪⎩，作出图象，如图所示：(2)将函数()f x 的图象向左平移1个单位，可得函数()1f x +的图象，如图所示：由()3511x x --=+-，解得76x =-． 所以不等式()(1)f x f x >+的解集为7,6⎛⎫-∞-⎪⎝⎭． 【点睛】本题主要考查画分段函数的图象，以及利用图象解不等式，意在考查学生的数形结合能力，属于基础题．4．(2016高考数学课标Ⅰ卷理科·第24题)(本小题满分10分)选修4—5：不等式选讲已知函数(x)123f x x =+--． (I )画出(x)y f =的图像； (II )求不等式(x)1f ൐的解集．【答案】 (I )见答案解析 (II )()()11353⎛⎫-∞+∞ ⎪⎝⎭，，，【官方解答】(I )()4133212342x x f x x x x x ⎧⎪--⎪⎪=--<<⎨⎪⎪-⎪⎩，≤，，≥ ，()y f x =如图所示：(II )由()f x 得表达式及图像，当()1f x =时，得1x =或3x =当()1f x =-时，得13x =或5x = 故()1f x ൐的解集为{}13x x <<；()1f x -൏的解集为153x x x ⎧⎫<>⎨⎬⎩⎭或 ()1f x >∴，解集为()()11353⎛⎫-∞+∞ ⎪⎝⎭ ，，，．【民间解答】(I )如上图所示：(II )()4133212342x x f x x x x x ⎧⎪--⎪⎪=--<<⎨⎪⎪-⎪⎩，≤，，≥()1f x >当1x -≤，41x ->，解得5x >或3x <1x -∴≤ 当312x -<<，321x ->，解得1x >或13x <113x -<<∴或312x << 当32x ≥，41x ->，解得5x >或3x < 332x <∴≤或5x >综上，13x <或13x <<或5x > ()1f x >∴，解集为()()11353⎛⎫-∞+∞ ⎪⎝⎭ ，，，．5．(2018年高考数学课标Ⅲ卷(理)·第23题)【选修4—5：不等式选讲】(10分)设函数()211f x x x =++-． (1)画出()y f x =的图象；(2)当[)0,x ∈+∞时，()f x ax b ≤+，求a b +的最小值．【答案】【官方答案解析】(1)()13,212,123,1x x f x x x x x ⎧-<-⎪⎪⎪=+-≤<⎨⎪≥⎪⎪⎩()y f x =的图像如图所示(2)由(1)知，()y f x =的图像与y 轴交点的纵坐标为2，且各部分所在直线斜率的最大值为3，故当且仅当3a ≥且2b ≥时，()f x ax b ≤+在[)0,+∞成立，因此a b +的最小值为5．【民间答案解析】(1)()211f x x x =++-3,112,12132x x x x x x ⎧⎪>⎪⎪=+-≤≤⎨⎪⎪-<-⎪⎩，可作出函数()f x 的图象如下图(2)依题意可知()f x ax b ≤+在[)1,+∞上恒成立，在[)0,1上也恒成立 当1x ≥时，()3f x x ax b =≤+恒成立即()30a x b -+≥在[)1,+∞上恒成立 所以30a -≥，且30a b -+≥，此时3a ≥，3a b +≥当01x ≤<时，()2f x x ax b =+≤+即()120a x b -+-≥恒成立 结合3a ≥，可知20b -≥即2b ≥综上可知32a b ≥⎧⎨≥⎩，所以当3a =，2b =时，a b +取得最小值5．题型五：不等式证明1．(2017年高考数学江苏文理科·第24题)[选修4-5:不等式选讲]已知为实数,且证明【答案】答案解析:证明:由柯西不等式得,直线的普通方程为．因为, ,所以, 因此2．(2022年高考全国甲卷数学(理)·第23题)已知a ，b ，c 均为正数，且22243a b c ++=，证明：(1)23a b c ++≤； (2)若2b c =，则113a c+≥． 【答案】(1)见答案解析 (2)见答案解析【答案解析】(1)证明：由柯西不等式有()()()222222221112a b c a b c ⎡⎤++++≥++⎣⎦， 所以23a b c ++≤，当且仅当21a b c ===时，取等号，所以23a b c ++≤； (2)证明：因为2b c =，0a >，0b >，0c >，由(1)得243a b c a c ++=+≤， 即043a c <+≤，所以1143a c ≥+， 由权方和不等式知()22212111293444a c a c a c a c++=+≥=≥++，当且仅当124a c =，即1a =，12c =时取等号， 所以113a c+≥ 3．(2020年高考课标Ⅲ卷理科·第23题)设a ，b ，c ∈R ，a +b +c =0，abc =1．(1)证明：ab +bc +ca <0；(2)用max{a ，b ，c }表示a ，b ，c 中的最大值，证明：max{a ，b ，c． 【答案】(1)证明见答案解析(2)证明见答案解析．答案解析：(1)2222()2220a b c a b c ab ac bc ++=+++++= ，,,,a b c d 22224,16,a b c d +=+=8.ac bd +≤l 22222()()()ac bd a b c d +++≤224a b +=2216c d +=2()64ac bd +≤8.ac bd +≤()22212ab bc ca a b c ∴++=-++ 1,,,abc a b c =∴ 均不为0，则2220a b c ++>，()222120ab bc ca a b c ∴++=-++<； (2)不妨设max{,,}a b c a =，由0,1a b c abc ++==可知，0,0,0a b c ><<，1,a b c a bc =--= ，()222322224b c b c bc bc bc a a a bc bc bc++++∴=⋅==≥=．当且仅当b c =时，取等号，a ∴≥，即max{,,}a b c ．【点睛】本题主要考查了不等式的基本性质以及基本不等式的应用，属于中档题．4．(2019·全国Ⅲ·理·第23题)设,,x y z R ∈，且1x y z ++=．(1)求222(1)(1)(1)x y z -++++的最小值；(2)若2221(2)(1)()3x y z a -+-+-≥成立，证明：3a -≤或1a -≥． 【答案】(1)43；(2)见详解． 【官方答案解析】(1)由于2[(1)(1)(1)]x y z -++++222(1)(1)(1)2[(1)(1)(1)(1)(1)(1)]x y z x y y z z x =-+++++-++++++-2223(1)(1)(1)x y z ⎡⎤-++++⎣⎦…故由已知得232(1)(1)143()x y z -++++≥，当且仅当511,,333x y z ==-=-时等号成立．所以232(1)(1)(1)x y z -++++的最小值为43． (2)由于2[(2)(1)()]x y z a -+-+-.222(2)(1)()2[(2)(1)(1)()()(2)]x y z a x y y z a z a x =-+-+-+--+--+--2223(2)(1)()x y z a ⎡⎤-+-+-⎣⎦…故由已知得2222(2)(2)(1)()3a x y z a +-+-+-…，当且仅当4122,,333aa a x y z ---===时等号成立．因此222(2)(1)()x y z a -+-+-的最小值为2(2)3a +由题设知2(2)133a +…，解得3a -≤或1a -≥．【解法2】柯西不等式法(1)22222222[(1)(1)(1)](111)[(1)(1)(1)](1)4x y z x y z x y z -++++++-++++=+++=≥，故2224(1)(1)(1)3x y z -++++≥，当且仅当511,,333x y z ==-=-时等号成立．所以222(1)(1)(1)x y z -++++的最小值为43． (2)2221(2)(1)()3x y z a -+-+-≥，所以222222[(2)(1)()](111)1x y z a -+-+-++≥．当且仅当4122,,333aa a x y z ---===时等号成立． 22222222[(2)(1)()](111)(21)(2)x y z a x y z a a -+-+-++=-+-+-=+成立．所以2(2)1a +≥成立，所以有3a -≤或1a -≥．【点评】本题两问思路一样，既可用基本不等式，也可用柯西不等式求解，属于中档题型．5．(2019·全国Ⅰ·理·第23题)已知a ，b ，c 为正数，且满足1abc =．证明：(1)222111a b c a b c++++≤； (2)333()()()24a b b c c a +++++≥．【答案】解：(1)因为2222222,2,2a b ab b c bc c a ac +++≥≥≥，又1abc =，故有222111ab bc ca a b c ab bc ca abc a b c ++++++==++≥．所以222111a b c a b c++++≤.(2)因为, , a b c 为正数且1abc =，故有333()()()a b b c c a +++++≥3(+)(+)(+)a b b c a c =324⨯⨯⨯=≥所以333()()()24a b b c c a +++++≥．6．(2014高考数学辽宁理科·第24题)(本小题满分10分)选修4-5：不等式选讲设函数()2|1|1f x x x =-+-，2()1681g x x x =-+，记()1f x ≤的解集为M ，()4g x ≤的解集为N ． (1)求M ；(2)当x M N ∈ 时，证明：221()[()]4x f x x f x +≤． 【答案】(1)[0，43]；(2)见答案解析． 答案解析：(1)由f (x )=2|x ﹣1|+x ﹣1≤1 可得1331x x ≥⎧⎨-≤⎩①，或111x x <⎧⎨-≤⎩②． 解①求得1≤x ≤43，解②求得 0≤x ＜1．综上，原不等式的解集为[0，43]．(2)由g (x )=16x 2﹣8x +1≤4，求得14-≤x ≤34，∴N =[14-，34]，∴M ∩N =[0，34]．∵当x ∈M ∩N 时，f (x )=1﹣x ，x 2f (x )+x [f (x )]2=xf (x )[x +f (x )]=21142x ⎛⎫-- ⎪⎝⎭≤14，故要证的不等式成立．7．(2014高考数学江苏·第24题)【选修4 - 5：不等式选讲】已知0,0x y >>，证明：22(1)(1)9x y x y xy ++++≥． 【答案】[选修4—4：不等式证明选讲]． 答案解析：本小题主要考查本小题满分10分．证法一：因为0,0x y >>，所以210x y ++≥>，故22(1)(1)9x y x y xy ++++≥=．证法二：(柯西不等式)22222(1)(1)(1)(1)(x y x y x y y x y x ++++=++++≥+29xy ≥+=．证法三：因为0,0x y >>，所以212x y x y ++≥+，212y x y x ++≥+．故222(1)(1)(2)(2)2()99x y x y x y y x x y xy xy ++++≥++=-+≥． (江苏苏州 褚小光) 证法四：因为0,0x y >>，所以212x y x y ++≥+，212y x y x ++≥+． 故2222(1)(1)(2)(2)225459x y x y x y y x x y xy xy xy xy ++++≥++=++≥+=． 8．(2014高考数学福建理科·第23题)(本小题满分7分)选修4—5：不等式选讲已知定义在R 上的函数21)(+++=x x x f 的最小值为a ． (I )求a 的值；(II )若r q p ,,为正实数，且a r q p =++，求证：3222≥++r q p ．(II22222222111()()(111)()9.p p q r p q r q r ≥⨯+⨯+⨯=++++=++即2223q pr ++≥．9．(2015高考数学新课标2理科·第24题)(本小题满分10分)选修4-5不等式选讲设,,,a b c d 均为正数，且a b c d +=+，证明：(Ⅰ)若ab cd >+>+>是a b c d -<-的充要条件．【答案】(Ⅰ)详见答案解析；(Ⅱ)详见答案解析．答案解析：(Ⅰ)因为2ab=++2cd=++由题设a b c d +=+，ab cd >，得22+>+>．(Ⅱ)(ⅰ)若a b c d -<-，则22()()a bc d -<-．即22()4()4ab abcd cd +-<+-．因为a bc d +=+，所以ab cd >>+>，则22>+，即a b ++>c d ++a b c d +=+，所以ab cd >，于是22()()4aba b ab -=+-2()4c d cd <+-2()c d =-．因此a b c d -<->a b c d -<-的充要条件．10．(2015高考数学湖南理科·第18题)设0,0a b >>，且11a b a b+=+．证明:(1)2a b +≥；(2)22a a +<与22b b +<不可能同时成立．【答案】(1)详见答案解析；(2)详见答案解析．分析：(1)将已知条件中的式子可等价变形为1=ab ，再由基本不等式即可得证；(2)利用反证法， 假设假设22<+a a 与22<+b b 同时成立，可求得10<<a ，10<<b ，从而与1=ab 矛盾，即可得证答案解析：由abba b a b a +=+=+11，0>a ，0>b ，得1=ab ，(1)由基本不等式及1=ab ，有22=≥+ab b a ，即2≥+b a ；(2)假设22<+a a 与22<+b b 同时成立，则由22<+a a 及0>a 得10<<a ，同理10<<b ，从而1<ab ，这与1=ab 矛盾，故22<+a a 与22<+b b 不可能成立．11．(2017年高考数学课标Ⅱ卷理科·第23题)[选修4-5：不等式选讲](10分)已知，证明：(1)；(2)．【答案】【命题意图】不等式证明，柯西不等式【基本解法】(1)解法一：由柯西不等式得：解法二：330,0,2a b a b >>+=33()()4a b a b ++≥2a b +≤55222222332()()))()4a b a b a b a b ⎡⎤⎡⎤++=+⋅+≥+=⎣⎦⎣⎦5566553325533()()()2a b a b a b ab a b a b ab a b a b++=+++=+++-33233332()2()4a b a b a b ≥++-=+=解法三：又，所以．当时，等号成立． 所以，，即．(2)解法一：由及得所以．解法二：(反证法)假设，则，两边同时立方得：，即，因为， 所以，即，矛盾，所以假设不成立，即．解法三：因为，所以：．又，所以: 。

,1
上恒成立,
x 2 max a x 2 min ,
1 a 5 , 2
a
的取值范围为
1,
5 2
.
【点睛】本题主要考查了绝对值不等式的求解,以及绝对值三角不等式的应用,其中解答中熟 记含绝对值不等式的解法,以及合理应用绝对值的三角不等式求解最值是解答的关键,着重 考查了推理与运算能力,属于中档题.
2
8．已知函数 f (x) x2 1, g(x) | x a | | 2x 1|, a R .
（1）当 a 1 时，解不等式 g(x2 ) 7 ；
2
2
（2）对任意 x1, x2 R ，若不等式 f (x1) ≥ g(x2 ) 恒成立，求实数 a 的取值范围.
试卷第 2页，总 6页
9．选修 4-5：不等式选讲
故 a 的取值范围为 (,5] [7, )
【点睛】本题考查含有绝对值的不等式的解法，绝对值的三角不等式，恒成立问题，考查了 计算化简，分析求值的能力，属中档题. 7．【详解】
（2）当 m 1时，函数 g(x) f (x) | x m | 的图象与 x 轴围成一个三角形，求实数 m 的取值范围.
21．设函数 f x 2x 4 1． （1）画出函数 y f x 的图象； （2）若不等式 f x ax 的解集非空，求 a 的取值范围．
试卷第 6页，总 6页
参考答案
试卷第 5页，总 6页
19．已知函数 f (x) | 3x 1| 2 | x 1| ．
（1）画出 y f (x) 的图像；
（2）求不等式 f (x) f (x 1) 的解集．
20．[选修 4-5：不等式选讲]
已知函数 f x 2x 2 5 . （1）解不等式： f x | x 1| ；

2015全国一卷理科
（24）本小题满分10分）选修4—5：不等式选讲
已知函数 =|x+1|-2|x-a|，a>0.
（Ⅰ）当a=1时，求不等式 f(x)>1的解集；
（Ⅱ）若f(x)的图像与x轴围成的三角形面积大于6，求a的取值范围
2015全国二卷理科
24．（本小题满分10分）
选修4-5：不等式选讲
设a，b，c，d均为正数，且a+b=c+d，证明：
近四年全国卷高考试题不等式选讲汇编
2016全国一卷理科
（24）（本小题满分10分），选修4—5：不等式选讲
已知函数f(x)=∣x+1∣-∣2x-3∣.
（I）在答题卡第（24）题图中画出y=f(x)的图像；
（II）求不等式∣f(x)∣﹥1的解集。
2016全国二卷理科
（24）（本小题满分10分），选修4—5：不等式选讲
（1）若ab>cd；则 ；
（2） 是 的充要条件。
2014全国一卷理科
24.（本小题满分10分）选修4—5：不等式选讲
若 ，且 .
(Ⅰ)求 的最小值；
（Ⅱ）是否存在 ，使得 ？并说明理由.
2014全国二卷理科
24.（本小题满分10）选修4-5：不等式选讲
设函数 =
（Ⅰ）证明： 2；
（Ⅱ）若 ，求 的取值范围.
2013全国一卷理科
（24）（本小题满分10分）选修4—5：不等式选讲
已知函数f(x)＝|2x－1|＋|2x＋a|，g(x)=x+3.
（Ⅰ）当a=-2时，求不等式f(x)＜g(x)的解集；
（Ⅱ）设a＞－1，且当x∈[－ ， )时，f(x)≤g(x)，求a的取值范围.

高考真题选修不等式选讲Document number【SA80SAB-SAA9SYT-SAATC-SA6UT-SA18】选修4-5 不等式选讲考点不等式选讲1.（2017?新课标Ⅰ,23）已知函数f（x）=﹣x2+ax+4，g（x）=|x+1|+|x﹣1|．（10分）(1)当a=1时，求不等式f（x）≥g（x）的解集；(2)若不等式f（x）≥g（x）的解集包含[﹣1，1]，求a的取值范围．1.（1）解：当a=1时，f（x）=﹣x2+x+4，是开口向下，对称轴为x= 的二次函数，g（x）=|x+1|+|x﹣1|= ，当x∈（1，+∞）时，令﹣x2+x+4=2x，解得x= ，g（x）在（1，+∞）上单调递增，f（x）在（1，+∞）上单调递减，∴此时f（x）≥g（x）的解集为（1，]；当x∈[﹣1，1]时，g（x）=2，f（x）≥f（﹣1）=2．当x∈（﹣∞，﹣1）时，g（x）单调递减，f（x）单调递增，且g （﹣1）=f（﹣1）=2．综上所述，f（x）≥g（x）的解集为[﹣1，]；（2）依题意得：﹣x2+ax+4≥2在[﹣1，1]恒成立，即x2﹣ax﹣2≤0在[﹣1，1]恒成立，则只需，解得﹣1≤a≤1，故a的取值范围是[﹣1，1]．2.（2017?新课标Ⅱ,23）已知a＞0，b＞0，a3+b3=2，证明：（Ⅰ）（a+b）（a5+b5）≥4；（Ⅱ）a+b≤2．2.证明：（Ⅰ）由柯西不等式得：（a+b）（a5+b5）≥（+）2=（a3+b3）2≥4，当且仅当= ，即a=b=1时取等号，（Ⅱ）∵a3+b3=2，∴（a+b）（a2﹣ab+b2）=2，∴（a+b）[（a+b）2﹣3ab]=2，∴（a+b）3﹣3ab（a+b）=2，∴=ab，由均值不等式可得：=ab≤（）2，∴（a+b）3﹣2≤ ，∴（a+b）3≤2，∴a+b≤2，当且仅当a=b=1时等号成立．3.（2017?新课标Ⅲ,23）已知函数f（x）=|x+1|﹣|x﹣2|．（Ⅰ）求不等式f（x）≥1的解集；（Ⅱ）若不等式f（x）≥x2﹣x+m的解集非空，求m的取值范围．3.（Ⅰ）∵f（x）=|x+1|﹣|x﹣2|= ，f（x）≥1，∴当﹣1≤x≤2时，2x﹣1≥1，解得1≤x≤2；当x＞2时，3≥1恒成立，故x＞2；综上，不等式f（x）≥1的解集为{x|x≥1}．（Ⅱ）原式等价于存在x∈R使得f（x）﹣x2+x≥m成立，即m≤[f（x）﹣x2+x]max，设g（x）=f（x）﹣x2+x．由（1）知，g（x）= ，当x≤﹣1时，g（x）=﹣x2+x﹣3，其开口向下，对称轴方程为x= ＞﹣1，∴g（x）≤g（﹣1）=﹣1﹣1﹣3=﹣5；当﹣1＜x＜2时，g（x）=﹣x2+3x﹣1，其开口向下，对称轴方程为x= ∈（﹣1，2），∴g（x）≤g（）=﹣+ ﹣1= ；当x≥2时，g（x）=﹣x2+x+3，其开口向下，对称轴方程为x= ＜2，∴g（x）≤g（2）=﹣4+2=3=1；综上，g（x）max= ，∴m的取值范围为（﹣∞，]．4.（2017?江苏,21D）已知a，b，c，d为实数，且a2+b2=4，c2+d2=16，证明ac+bd≤8．4. 证明：∵a 2+b 2=4，c 2+d 2=16，令a=2cosα，b=2sinα，c=4cosβ，d=4sinβ．∴ac+bd=8（cosαcosβ+sinαsinβ）=8cos （α﹣β）≤8．当且仅当cos （α﹣β）=1时取等号． 因此ac+bd≤8．5.(2016·全国Ⅰ，24)已知函数f (x )＝|x ＋1|－|2x －3|. (1)在图中画出y ＝f (x )的图象； (2)求不等式|f (x )|>1的解集.5.解(1)f (x )＝⎩⎪⎨⎪⎧x －4，x ≤－1，3x －2，－1<x ≤ 32，－x ＋4，x >32，y ＝f (x )的图象如图所示.(2)当f (x )＝1时，可得x ＝1或x ＝3；当f (x )＝－1时，可得x ＝13或x ＝5，故f (x )>1的解集为{x |1<x <3}；f (x )<－1的解集为⎩⎨⎧⎭⎬⎫x |x <13或x >5.所以|f (x )|>1的解集为⎩⎨⎧⎭⎬⎫x |x <13或1<x <3或x >5.6.(2016·全国Ⅲ，24)已知函数f (x )＝|2x －a |＋a . (1)当a ＝2时，求不等式f (x )≤6的解集；(2)设函数g (x )＝|2x －1|.当x ∈R 时，f (x )＋g (x )≥3，求a 的取值范围.6.解 (1)当a ＝2时，f (x )＝|2x －2|＋2.解不等式|2x －2|＋2≤6得－1≤x ≤3.因此f (x )≤6的解集为{x |－1≤x ≤3}.(2)当x ∈R 时，f (x )＋g (x )＝|2x －a |＋a ＋|1－2x |≥|2x －a ＋1－2x |＋a ＝|1－a |＋a ，所以当x ∈R 时，f (x )＋g (x )≥3等价于|1－a |＋a ≥3.① 当a ≤1时，①等价于1－a ＋a ≥3，无解. 当a ＞1时，①等价于a －1＋a ≥3，解得a ≥2. 所以a 的取值范围是[2，＋∞).7.(2016·全国Ⅱ，24)已知函数f (x )＝⎪⎪⎪⎪⎪⎪x －12＋⎪⎪⎪⎪⎪⎪x ＋12，M 为不等式f (x )<2的解集. (1)求M ；(2)证明：当a ，b ∈M 时，|a ＋b |<|1＋ab |.7.(1)解 f (x )＝⎩⎪⎨⎪⎧－2x ，x ≤－12，1，－12<x <12，2x ，x ≥12.当x ≤－12时,由f (x )<2得－2x <2，解得x >－1,所以,-1<x ≤-12；当-12<x <12时，f (x )<2； 当x ≥12时，由f (x )<2得2x <2，解得x <1，所以，-12<x <1.所以f (x )<2的解集M ＝{x |－1<x <1}.(2)证明 由(1)知，当a ,b ∈M 时,-1<a <1,-1<b <1,从而(a ＋b )2-(1＋ab )2＝a 2＋b 2-a 2b 2-1＝(a 2-1)(1-b 2)<0，即(a ＋b )2<(1＋ab )2，因此|a ＋b |<|1＋ab |.8.(2015·重庆，16)若函数f (x )＝|x ＋1|＋2|x －a |的最小值为5，则实数a ＝________.或－6 [由绝对值的性质知f (x )的最小值在x ＝-1或x ＝a 时取得,若f (-1)＝2|－1-a |＝5,a ＝32或a ＝－72，经检验均不合适；若f (a )＝5，则|x ＋1|＝5，a ＝4或a ＝－6，经检验合题意，因此a ＝4或a ＝－6.]9.(2015·陕西，24)已知关于x 的不等式|x ＋a |＜b 的解集为{x |2＜x ＜4}.(1)求实数a ，b 的值； (2)求at ＋12＋bt 的最大值.9.解(1)由|x ＋a |＜b ，得－b －a ＜x ＜b －a ，则⎩⎪⎨⎪⎧－b －a ＝2，b －a ＝4，解得a＝－3，b ＝1. (2)－3t ＋12＋t ＝34－t ＋t ≤[（3）2＋12][（4－t ）2＋（t ）2]＝24－t ＋t ＝4， 当且仅当4－t 3＝t1，即t ＝1时等号成立，故(－3t ＋12＋t )max＝4.10.(2015·新课标全国Ⅰ，24)已知函数f (x )＝|x ＋1|－2|x －a |，a >0.(1)当a ＝1时，求不等式f (x )>1的解集；(2)若f (x )的图象与x 轴围成的三角形面积大于6，求a 的取值范围. 10.解 (1)当a ＝1时，f (x )>1化为|x ＋1|－2|x －1|－1>0. 当x ≤－1时，不等式化为x －4>0，无解； 当－1<x <1时，不等式化为3x －2>0，解得23<x <1；当x ≥1时，不等式化为－x ＋2>0，解得1≤x <2.所以f (x )>1的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪23<x <2.(2)由题设可得，f (x )＝⎩⎪⎨⎪⎧x －1－2a ，x <－1，3x ＋1－2a ，－1≤x ≤a ，－x ＋1＋2a ，x >a .所以函数f (x )的图象与x 轴围成的三角形的三个顶点分别为A ⎝⎛⎭⎪⎫2a －13，0,B (2a ＋1,0),C (a ,a +1)， △ABC 的面积为23(a ＋1)2.由题设得23(a ＋1)2>6，故a >2.所以a 的取值范围为(2，＋∞).11.(2015·新课标全国Ⅱ，24)设a 、b 、c 、d 均为正数，且a ＋b ＝c ＋d ，证明：(1)若ab ＞cd ，则a ＋b ＞c ＋d ；(2)a ＋b ＞c ＋d 是|a －b |＜|c －d |的充要条件.11.证明 (1)因为(a ＋b )2＝a ＋b ＋2ab ，(c ＋d )2＝c ＋d ＋2cd ，由题设a ＋b ＝c ＋d ，ab ＞cd 得(a ＋b )2＞(c ＋d )2.因此a ＋b ＞c ＋d .(2)①若|a －b |＜|c －d |，则(a －b )2＜(c －d )2，即(a ＋b )2－4ab ＜(c ＋d )2－4cd .因为a ＋b ＝c ＋d ，所以ab ＞cd .由(1)得a ＋b ＞c ＋d . ②若a ＋b ＞c ＋d ，则(a ＋b )2＞(c ＋d )2，即a ＋b ＋2ab ＞c ＋d ＋2cd .因为a ＋b ＝c ＋d ，所以ab ＞cd ，于是(a －b )2＝(a ＋b )2－4ab ＜(c ＋d )2－4cd ＝(c －d )2.因此|a －b |＜|c －d |.综上，a ＋b ＞c ＋d 是|a －b |＜|c －d |的充要条件.12.(2014·广东，9)不等式|x －1|＋|x ＋2|≥5的解集为________.12.{x |x ≤－3或x ≥2} [原不等式等价于⎩⎪⎨⎪⎧x ≥1，（x －1）＋（x ＋2）≥5或⎩⎪⎨⎪⎧－2<x <1，－（x －1）＋（x ＋2）≥5或⎩⎪⎨⎪⎧x ≤－2，－（x －1）－（x ＋2）≥5，解得x ≥2或x ≤－3.故原不等式的解集为{x |x ≤－3或x ≥2}.]13.(2014·湖南，13)若关于x 的不等式|ax －2|<3的解集为⎩⎨⎧⎭⎬⎫x |－53<x <13，则a ＝________.13.－3 [依题意，知a ≠0.|ax －2|<3?－3<ax －2<3?－1<ax <5，当a >0时，不等式的解集为⎝ ⎛⎭⎪⎫－1a ，5a ，从而有⎩⎪⎨⎪⎧5a ＝13，－1a ＝－53，此方程组无解.当a <0时，不等式的解集为⎝ ⎛⎭⎪⎫5a，－1a ，从而有⎩⎪⎨⎪⎧5a ＝－53，－1a ＝13，解得a ＝－3.]14.(2014·重庆，16)若不等式|2x －1|＋|x ＋2|≥a 2＋12a ＋2对任意实数x 恒成立，则实数a 的取值范围是________.[令f (x )＝|2x -1|＋|x +2|,易求得f (x )min ＝52,依题意得a 2+12a +2≤52?-1≤a ≤12.]15.(2014·新课标全国Ⅱ，24)设函数f (x )＝|x ＋1a|＋|x －a |(a >0).(1)证明：f (x )≥2；(2)若f (3)<5，求a 的取值范围.15.(1)证明 由a >0，有f (x )＝|x ＋1a |＋|x －a |≥|x ＋1a－(x －a )|＝1a＋a ≥2.所以f (x )≥2.(2)解 f (3)＝|3＋1a |＋|3－a |.当a >3时，f (3)＝a ＋1a，由f (3)<5得3<a <5＋212.当0<a ≤3时，f (3)＝6－a ＋1a ，由f (3)<5得1＋52＜a ≤3.综上，a 的取值范围是⎝ ⎛⎭⎪⎪⎫1＋52，5＋21216.(2014·天津，19)已知q 和n 均为给定的大于1的自然数.设集合M ＝{0,1,2，…，q －1}，集合A ＝{x |x ＝x 1＋x 2q ＋…＋x n q n －1，x i ∈M ，i ＝1,2，…，n }.(1)当q ＝2，n ＝3时，用列举法表示集合A ；(2)设s ，t ∈A ，s ＝a 1＋a 2q ＋…＋a n q n －1，t ＝b 1＋b 2q ＋…＋b n q n －1，其中a i ，b i ∈M ，i ＝1,2，…，n .证明：若a n <b n ，则s <t .16.(1)解当q＝2,n＝3时,M＝{0,1},A＝{x|x＝x1＋x2·2＋x3·22,x i∈M,i＝1,2,3}.可得,A＝{0,1,2,3,4,5,6,7}.(2)证明由s,t∈A,s＝a1＋a2q＋…＋a n q n－1，t＝b1＋b2q＋…＋b n q n－1，ai，b i∈M，i＝1，2，…，n及a n<b n,可得s-t＝(a1－b1)＋(a2－b2)q＋…＋(a n－1－b n－1)q n－2＋(a n－b n)q n－1≤(q-1)＋(q-1)q+…+(q-1)·q n－2－q n－1＝（q－1）（1－q n－1）1－q－q n－1＝-1<0.所以，s<t.。

专练1．已知函数f (x )＝|2x －1|＋|x －2a |.(1)当a ＝1时，求f (x )≤3的解集；(2)当x ∈[1，2]时，f (x )≤3恒成立，求实数a 的取值范围．2．已知函数f (x )＝|2x ＋1|＋|2x －3|.(1)求不等式f (x )≤6的解集；(2)若关于x 的不等式f (x )<|a －1|的解集不是空集，求实数a 的取值范围．3．已知函数f (x )＝|x ＋3|－|x －2|.(1)求不等式f (x )≥3的解集；(2)若f (x )≥|a －4|有解，求a 的取值范围．4．设不等式－2＜|x －1|－|x ＋2|＜0的解集为M ，a ，b ∈M .(1)证明：|13a ＋16b |＜14；(2)比较|1－4ab |与2|a －b |的大小，并说明理由．5．设函数f (x )＝|x －3|－|x ＋1|，x ∈R .(1)解不等式f (x )<－1；(2)设函数g (x )＝|x ＋a |－4，且g (x )≤f (x )在x ∈[－2，2]上恒成立，求实数a 的取值范围．6．已知a >0，b >0，a ＋b ＝1，求证：(1)1a ＋1b ＋1ab ≥8；7．已知关于x 的不等式m －|x －2|≥1，其解集为[0，4]．(1)求m 的值；(2)若a ，b 均为正实数，且满足a ＋b ＝m ，求a 2＋b 2的最小值．8．已知a ，b 均为正数，且a ＋b ＝1，证明：(1)(ax ＋by )2≤ax 2＋by 2；≥252.9．已知二次函数f (x )＝x 2＋ax ＋b (a ，b ∈R )的定义域为[－1，1]，且|f (x )|的最大值为M .(1)证明：|1＋b|≤M；(2)证明：M≥12.10．已知a，b，c为非零实数，且a2＋b2＋c2＋1－m＝0，1a2＋4b2＋9c2＋1－2m＝0.(1)求证：1a2＋4b2＋9c2≥36a2＋b2＋c2；(2)求实数m的取值范围．11．已知函数f(x)＝m－|x－1|－|x－2|，m∈R，且f(x＋1)≥0的解集为[0，1]．(1)求m的值；(2)若a，b，c，x，y，z∈R，且x2＋y2＋z2＝a2＋b2＋c2＝m，求证：ax＋by＋cz≤1. 12．已知函数f(x)＝|x－a|，其中a>1.(1)当a＝2时，求不等式f(x)≥4－|x－4|的解集；(2)已知关于x的不等式|f(2x＋a)－2f(x)|≤2的解集为{x|1≤x≤2}，求a的值．13．设函数f(x)＝|x＋1a|＋|x－a|(a>0)．(1)证明：f(x)≥2；(2)若f(3)<5，求a的取值范围．14．设函数f(x)＝2|x－1|＋x－1，g(x)＝16x2－8x＋1.记f(x)≤1的解集为M，g(x)≤4的解集为N.(1)求M；(2)当x∈M∩N时，证明：x2f(x)＋x[f(x)]2≤14.15．设不等式－2＜|x－1|－|x＋2|＜0的解集为M，a，b∈M.(1)证明：|13a＋16b|＜14(2)比较|1－4ab|与2|a－b|的大小，并说明理由．16．已知函数f(x)＝|x＋1|＋|x－3|，g(x)＝a－|x－2|.(1)若关于x的不等式f(x)<g(x)有解，求实数a的取值范围；(2)若关于x的不等式f(x)<g(x)a＋b的值．17．已知函数f(x)＝|x－a|.(1)若对x∈[0,4]不等式f(x)≤3恒成立，求实数a的取值范围；(2)当a＝2时，若f(x)＋f(x＋5)≥m对一切实数x恒成立，求实数m的取值范围．18．已知x，y∈R，m＋n＝7，f(x)＝|x－1|－|x＋1|.(1)解不等式f (x )≥(m ＋n )x ；(2)设max{a ，b }，a ≥b ，，a <b ，求F ＝max{|x 2－4y ＋m |，|y 2－2x ＋n |}的最小值．19．已知x ，y ∈R .(1)若x ，y 满足|x －3y |＜12，|x ＋2y |＜16，求证：|x |＜310；(2)求证：x 4＋16y 4≥2x 3y ＋8xy 3.20．已知a ，b ，c ，m ，n ，p 都是实数，且a 2＋b 2＋c 2＝1，m 2＋n 2＋p 2＝1.(1)证明：|am ＋bn ＋cp |≤1；(2)若abc ≠0，证明：m 4a 2＋n 4b 2＋p 4c 2≥1.21．已知函数f (x )＝|x －1|.(1)求不等式2f (x )－x ≥2的解集；(2)对∀x ∈R ，a ，b ，c ∈(0，＋∞)，求证：|x －1|－|x ＋5|≤1a 3＋1b 3＋1c 3＋3abc .22．已知函数f (x )＝4－|x |－|x －3|.(1)求不等式f 的解集；(2)若p ，q ，r 为正实数，且13p ＋12q ＋1r ＝4，求3p ＋2q ＋r 的最小值．23．设函数f (x )＝|x ＋a |－|x －1－a |.(1)当a ＝1时，解不等式f (x )≥12；(2)若对任意a ∈[0,1]，不等式f (x )≥b 的解集不为空集，求实数b 的取值范围．高考押题专练1．已知函数f (x )＝|2x －1|＋|x －2a |.(1)当a ＝1时，求f (x )≤3的解集；(2)当x ∈[1，2]时，f (x )≤3恒成立，求实数a 的取值范围．【解析】(1)当a ＝1时，由f (x )≤3，可得|2x －1|＋|x －2|≤3，＜12，－2x ＋2－x ≤3x ＜2，－1＋2－x ≤3≥2，x －1＋x －2≤3.解①得0≤x ＜12，解②得12≤x ＜2，解③得x ＝2.综上可得，0≤x ≤2，即不等式的解集为[0，2]．(2)∵当x ∈[1，2]时，f (x )≤3恒成立，即|x －2a |≤3－|2x －1|＝4－2x ，故2x －4≤2a －x ≤4－2x ，即3x －4≤2a ≤4－x .再根据3x －4在x ∈[1，2]上的最大值为6－4＝2，4－x 的最小值为4－2＝2，∴2a ＝2，∴a ＝1，即a 的取值范围为{1}．2．已知函数f (x )＝|2x ＋1|＋|2x －3|.(1)求不等式f (x )≤6的解集；(2)若关于x 的不等式f (x )<|a －1|的解集不是空集，求实数a 的取值范围．【解析】(1)原不等式等价于>32，2x ＋1）＋（2x －3）≤6－12≤x ≤32，2x ＋1）－（2x －3）≤6或<－12，2x ＋1）－（2x －3）≤6，解得32<x ≤2或－12≤x ≤32或－1≤x <－12.∴原不等式的解集为{x |－1≤x ≤2}．(2)∵f (x )＝|2x ＋1|＋|2x －3|≥|(2x ＋1)－(2x －3)|＝4，∴|a －1|>4，∴a <－3或a >5，∴实数a的取值范围为(－∞，－3)∪(5，＋∞)．3．已知函数f(x)＝|x＋3|－|x－2|.(1)求不等式f(x)≥3的解集；(2)若f(x)≥|a－4|有解，求a的取值范围．【解析】(1)f(x)＝|x＋3|－|x－2|≥3，当x≥2时，有x＋3－(x－2)≥3，解得x≥2；当x≤－3时，－x－3＋(x－2)≥3，解得x∈∅；当－3<x<2时，有2x＋1≥3，解得1≤x<2.综上，f(x)≥3的解集为{x|x≥1}．(2)由绝对值不等式的性质可得，||x＋3|－|x－2||≤|(x＋3)－(x－2)|＝5，则有－5≤|x＋3|－|x－2|≤5.若f(x)≥|a－4|有解，则|a－4|≤5，解得－1≤a≤9.所以a的取值范围是[－1，9]．4．设不等式－2＜|x－1|－|x＋2|＜0的解集为M，a，b∈M.(1)证明：|13a＋16b|＜14；(2)比较|1－4ab|与2|a－b|的大小，并说明理由．【解析】(1)证明：记f(x)＝|x－1|－|x＋2|，x≤－2，2x－1，－2＜x＜1，3，x≥1.由－2＜－2x－1＜0，解得－12＜x＜12，则M－12，所以|13a＋16b|≤13|a|＋16|b|＜13×12＋16×12＝14.(2)由(1)得a2＜14，b2＜14.因为|1－4ab|2－4|a－b|2＝(1－8ab＋16a2b2)－4(a2－2ab＋b2)＝(4a2－1)(4b2－1)＞0，所以|1－4ab|2＞4|a－b|2，故|1－4ab|＞2|a－b|.5．设函数f(x)＝|x－3|－|x＋1|，x∈R.(1)解不等式f(x)<－1；(2)设函数g(x)＝|x＋a|－4，且g(x)≤f(x)在x∈[－2，2]上恒成立，求实数a的取值范围．【解析】(1)函数f(x)＝|x－3|－|x＋1|，x<－1－2x，－1≤x≤3，4，x>3，故由不等式f(x)<－1可得，x>3－2x<－1，1≤x≤3.解得x>32.(2)函数g(x)≤f(x)在x∈[－2，2]上恒成立，即|x＋a|－4≤|x－3|－|x＋1|在x∈[－2，2]上恒成立，在同一个坐标系中画出函数f(x)和g(x)的图象，如图所示．故当x∈[－2，2]时，若0≤－a≤4，则函数g(x)的图象在函数f(x)的图象的下方，g(x)≤f(x)在x∈[－2，2]上恒成立，求得－4≤a≤0，故所求的实数a的取值范围为[－4，0]．6．已知a>0，b>0，a＋b＝1，求证：(1)1a＋1b＋1ab≥8；【解析】证明：(1)∵a＋b＝1，a>0，b>0，∴1a＋1b＋1ab＝1a＋1b＋a＋bab＝＝4≥4ba ·ab＋4＝8(当且仅当a＝b＝12时，等号成立)，∴1a＋1b＋1ab≥8.(2)＝1a＋1b＋1ab＋1，由(1)知1a＋1b＋1ab≥8.7．已知关于x的不等式m－|x－2|≥1，其解集为[0，4]．(1)求m的值；(2)若a，b均为正实数，且满足a＋b＝m，求a2＋b2的最小值．【解析】(1)不等式m－|x－2|≥1可化为|x－2|≤m－1，∴1－m≤x－2≤m－1，即3－m≤x≤m＋1.∵其解集为[0，4]－m＝0，＋1＝4，∴m＝3.(2)由(1)知a＋b＝3，∵(a2＋b2)(12＋12)≥(a×1＋b×1)2＝(a＋b)2＝9，∴a2＋b2≥92，∴a2＋b2的最小值为92.8．已知a，b均为正数，且a＋b＝1，证明：(1)(ax＋by)2≤ax2＋by2；≥252.【解析】证明：(1)(ax＋by)2－(ax2＋by2)＝a(a－1)x2＋b(b－1)y2＋2abxy，因为a＋b＝1，所以a－1＝－b，b－1＝－a.又a ，b 均为正数，所以a (a －1)x 2＋b (b －1)y 2＋2abxy＝－ab (x 2＋y 2－2xy )＝－ab (x －y )2≤0，当且仅当x ＝y 时等号成立．所以(ax ＋by )2≤ax 2＋by 2.＝4＋a 2＋b 24＋a 2＋b 2＋（a ＋b ）2a 2＋（a ＋b ）2b 2＝4＋a 2＋b 2＋1＋2b a ＋b 2a 2＋a 2b 2＋2a b ＋1＝4＋(a 2＋b 2)＋2＋＋（a ＋b ）22＋2＋4＋2＝252.当且仅当a ＝b 时等号成立．9．已知二次函数f (x )＝x 2＋ax ＋b (a ，b ∈R )的定义域为[－1，1]，且|f (x )|的最大值为M .(1)证明：|1＋b |≤M ；(2)证明：M ≥12.【解析】证明：(1)∵M ≥|f (－1)|＝|1－a ＋b |，M ≥|f (1)|＝|1＋a ＋b |，∴2M ≥|1－a ＋b |＋|1＋a ＋b |≥|(1－a ＋b )＋(1＋a ＋b )|＝2|1＋b |，∴M ≥|1＋b |.(2)依题意，M ≥|f (－1)|，M ≥|f (0)|，M ≥|f (1)|.又|f (－1)|＝|1－a ＋b |，|f (1)|＝|1＋a ＋b |，|f (0)|＝|b |.∴4M ≥|f (－1)|＋2|f (0)|＋|f (1)|＝|1－a ＋b |＋2|b |＋|1＋a ＋b |≥|(1－a ＋b )－2b ＋(1＋a ＋b )|＝2.∴M ≥12.10．已知a ，b ，c 为非零实数，且a 2＋b 2＋c 2＋1－m ＝0，1a 2＋4b 2＋9c 2＋1－2m ＝0.(1)求证：1a 2＋4b 2＋9c 2≥36a 2＋b 2＋c2；(2)求实数m 的取值范围．【解析】(1)证明：由柯西不等式得2(a 2＋b 2＋c 2a ＋2b ·b ＋3c·，2(a2＋b2＋c2)≥36.∴1a2＋4b2＋9c2≥36a2＋b2＋c2.(2)由已知得a2＋b2＋c2＝m－1，1a2＋4b2＋9c2＝2m－1，∴(m－1)(2m－1)≥36，即2m2－3m－35≥0，解得m≤－72或m≥5.又a2＋b2＋c2＝m－1>0，1a2＋4b2＋9c2＝2m－1>0，∴m≥5.即实数m的取值范围是[5，＋∞)．11．已知函数f(x)＝m－|x－1|－|x－2|，m∈R，且f(x＋1)≥0的解集为[0，1]．(1)求m的值；(2)若a，b，c，x，y，z∈R，且x2＋y2＋z2＝a2＋b2＋c2＝m，求证：ax＋by＋cz≤1.【解析】(1)由f(x＋1)≥0得|x|＋|x－1|≤m.∵|x|＋|x－1|≥1恒成立，∴若m<1，不等式|x|＋|x－1|≤m的解集为∅，不合题意．若m≥1，①当x<0时，得x≥1－m2，则1－m2≤x<0；②当0≤x≤1时，得x＋1－x≤m，即m≥1恒成立；③当x>1时，得x≤m＋12，则1<x≤m＋12.综上可知，不等式|x|＋|x－1|≤m的解集为1－m2，m＋12.由题意知，原不等式的解集为[0，1]，0，1，解得m＝1.(2)证明：∵x2＋a2≥2ax，y2＋b2≥2by，z2＋c2≥2cz，三式相加，得x2＋y2＋z2＋a2＋b2＋c2≥2ax＋2by＋2cz.由题设及(1)，知x2＋y2＋z2＝a2＋b2＋c2＝m＝1，∴2≥2(ax ＋by ＋cz )，即ax ＋by ＋cz ≤1，得证．12．已知函数f (x )＝|x －a |，其中a >1.(1)当a ＝2时，求不等式f (x )≥4－|x －4|的解集；(2)已知关于x 的不等式|f (2x ＋a )－2f (x )|≤2的解集为{x |1≤x ≤2}，求a 的值．【解析】(1)当a ＝2时，f (x )＋|x －4|＝2x ＋6，x ≤2，，2<x <4，x ＋6，x ≥4.当x ≤2时，由f (x )≥4－|x －4|得－2x ＋6≥4，解得x ≤1；当2<x <4时，f (x )≥4－|x －4|无解；当x ≥4时，由f (x )≥4－|x －4|得2x －6≥4.解得x ≥5.所以f (x )≥4－|x －4|的解集为{x |x －1或x ≥5}．(2)记h (x )＝f (2x ＋a )－2f (x )，则h (x )2a ，x ≤0，x －2a ，0<x <a ，a ，x ≥a .由|h (x )|≤2，解得a －12≤x ≤a ＋12.又已知|h (x )|≤2的解集为{x |1≤x ≤2}．1，2，∴a ＝3.13．设函数f (x )＝|x ＋1a |＋|x －a |(a >0)．(1)证明：f (x )≥2；(2)若f (3)<5，求a 的取值范围．【解析】(1)证明：由a >0，有f (x )＝|x ＋1a |＋|x －a |≥|x ＋1a －x －a |＝1a ＋a ≥2.所以f (x )≥2.(2)f (3)＝|3＋1a |＋|3－a |.当a >3时，f (3)＝a ＋1a ，由f (3)<5得3<a <5＋212.当0<a ≤3时，f (3)＝6－a ＋1a ，由f (3)<5得1＋52<a ≤3.综上，a 14．设函数f (x )＝2|x －1|＋x －1，g (x )＝16x 2－8x ＋1.记f (x )≤1的解集为M ，g (x )≤4的解集为N .(1)求M ；(2)当x ∈M ∩N 时，证明：x 2f (x )＋x [f (x )]2≤14.【解析】(1)f (x )x －3，x ∈[1，＋∞ ，－x ，x ∈－∞，1 .当x ≥1时，由f (x )＝3x －3≤1得x ≤43，故1≤x ≤43；当x ＜1时，由f (x )＝1－x ≤1得x ≥0，故0≤x ＜1.所以f (x )≤1的解集M ＝{x |0≤x ≤43}．(2)证明：由g (x )＝16x 2－8x ＋1≤4得≤4，解得－14≤x ≤34，因此N ＝{x |－14≤x ≤324}，故M ∩N ＝{x |0≤x ≤34}．当x ∈M ∩N 时，f (x )＝1－x ，于是x 2f (x )＋x ·[f (x )]2＝xf (x )[x ＋f (x )]＝xf (x )＝x (1－x )＝14－≤14.15．设不等式－2＜|x －1|－|x ＋2|＜0的解集为M ，a ，b ∈M .(1)证明：|13a ＋16b |＜14(2)比较|1－4ab |与2|a －b |的大小，并说明理由．【解析】(1)证明：设f (x )＝|x －1|－|x ＋2|，x ≤－12x －1，－1＜x ＜13，x ≥1由－2＜－2x －1＜0，解得－12＜x ＜12，则M －12，所以|13a ＋16b |≤13|a |＋16|b |＜13×12＋16×12＝14.(2)由(1)得a 2＜14，b 2＜14.因为|1－4ab |2－4|a －b |2＝(1－8ab ＋16a 2b 2)－4(a 2－2ab ＋b 2)＝(4a 2－1)(4b 2－1)＞0，所以|1－4ab |2＞4|a －b |2，故|1－4ab |＞2|a －b |.16．已知函数f (x )＝|x ＋1|＋|x －3|，g (x )＝a －|x －2|.(1)若关于x 的不等式f (x )<g (x )有解，求实数a 的取值范围；(2)若关于x 的不等式f (x )<g (x )a ＋b 的值．【解析】(1)当x ＝2时，g (x )＝a －|x －2|取得最大值a ，∵f (x )＝|x ＋1|＋|x －3|≥4，当且仅当－1≤x ≤3，f (x )取得最小值4，又∵关于x 的不等式f (x )<g (x )有解，∴a >4，即实数a 的取值范围是(4，＋∞)．(2)当x ＝72时，f (x )＝5，则＝－72＋a ＋2＝5，解得a ＝132，∴当x <2时，g (x )＝x ＋92，令g (x )＝x ＋92＝4，得x ＝－12∈(－1,3)，∴b ＝－12，则a ＋b ＝6.17．已知函数f (x )＝|x －a |.(1)若对x ∈[0,4]不等式f (x )≤3恒成立，求实数a 的取值范围；(2)当a ＝2时，若f (x )＋f (x ＋5)≥m 对一切实数x 恒成立，求实数m 的取值范围．【解析】(1)由f (x )≤3，得|x －a |≤3，解得a －3≤x ≤a ＋3，∴不等式f (x )≤3的解集M ＝[a －3，a ＋3]，根据题意知[0,4]⊆M －3≤0，＋3≥4，∴1≤a ≤3.(2)当a ＝2时，f (x )＝|x －2|，设g (x )＝f (x )＋f (x ＋5)＝|x －2|＋|x ＋3|.由|x －2|＋|x ＋3|≥|(x －2)－(x ＋3)|＝5(当且仅当－3≤x ≤2时等号成立)，∴g (x )的最小值为5，因此，若g (x )＝f (x )＋f (x ＋5)≥m 对x ∈R 恒成立，则实数m 的取值范围是(－∞，5]．18．已知x ，y ∈R ，m ＋n ＝7，f (x )＝|x －1|－|x ＋1|.(1)解不等式f (x )≥(m ＋n )x ；(2)设max{a ，b }，a ≥b ，，a <b ，求F ＝max{|x 2－4y ＋m |，|y 2－2x ＋n |}的最小值．【解析】(1)f (x )≥(m ＋n )x ⇔|x －1|－|x ＋1|≥7x ，当x ≤－1时，2≥7x ，恒成立，当－1<x <1时，－2x ≥7x ，即－1<x ≤0；当x ≥1时，－2≥7x ，即x ∈∅，综上可知，不等式的解集为{x |x ≤0}．(2)∵F ≥|x 2－4y ＋m |，F ≥|y 2－2x ＋n |，∴2F ≥|x 2－4y ＋m |＋|y 2－2x ＋n |≥|(x －1)2＋(y －2)2＋m ＋n －5|＝|(x －1)2＋(y －2)2＋2|≥2，∴F ≥1，F min ＝1.19．已知x ，y ∈R .(1)若x ，y 满足|x －3y |＜12，|x ＋2y |＜16，求证：|x |＜310；(2)求证：x 4＋16y 4≥2x 3y ＋8xy 3.【证明】(1)∵|5x |＝|2(x －3y )＋3(x ＋2y )|≤|2(x －3y )|＋|3(x ＋2y )|<2×12＋3×16＝32，∴|x |<310.(2)∵x 4＋16y 4－(2x 3y ＋8xy 3)＝x 3(x －2y )－8y 3(x －2y )＝(x －2y )(x 3－8y 3)＝(x －2y )2(x 2＋2xy ＋4y 2)＝(x －2y )2[(x 2＋2xy ＋y 2)＋3y 2]≥0，∴x 4＋16y 4≥2x 3y ＋8xy 3.20．已知a ，b ，c ，m ，n ，p 都是实数，且a 2＋b 2＋c 2＝1，m 2＋n 2＋p 2＝1.(1)证明：|am ＋bn ＋cp |≤1；(2)若abc ≠0，证明：m 4a 2＋n 4b 2＋p 4c 2≥1.【证明】(1)因为|am ＋bn ＋cp |≤|am |＋|bn |＋|cp |，a 2＋b 2＋c 2＝1，m 2＋n 2＋p 2＝1，所以|am |＋|bn |＋|cp |≤a 2＋m 22＋b 2＋n 22＋c 2＋p 22＝a 2＋b 2＋c 2＋m 2＋n 2＋p 22＝1，即|am ＋bn ＋cp |≤1.(2)因为a 2＋b 2＋c 2＝1，m 2＋n 2＋p 2＝1，所以m 4a 2＋n 4b 2＋p 4c 2＋n 4b 2＋a 2＋b 2＋c 2)a ＋n 2b ·b ＋p 2c ·＝(m 2＋n 2＋p 2)2＝1.所以m 4a 2＋n 4b 2＋p 4c 2≥1.21．已知函数f (x )＝|x －1|.(1)求不等式2f (x )－x ≥2的解集；(2)对∀x ∈R ，a ，b ，c ∈(0，＋∞)，求证：|x －1|－|x ＋5|≤1a 3＋1b 3＋1c 3＋3abc .(1)【解析】令g (x )＝2f (x )－x ＝2|x －1|－x－2，x ≥1，3x ＋2，x <1，当x ≥1时，由x －2≥2，得x ≥4，当x <1时，由－3x ＋2≥2，得x ≤0，∴不等式的解集为(－∞，0]∪[4，＋∞)．(2)【证明】|x －1|－|x ＋5|≤|x －1－(x ＋5)|＝6，又∵a ，b ，c >0，∴1a 3＋1b 3＋1c 3＋3abc≥331a 3·1b 3·1c 3＋3abc＝3abc ＋3abc ≥23abc ·3abc ＝6，当且仅当a ＝b ＝c ＝1时取等号，∴|x －1|－|x ＋5|≤1a 3＋1b 3＋1c 3＋3abc .22．已知函数f (x )＝4－|x |－|x －3|.(1)求不等式f 的解集；(2)若p ，q ，r 为正实数，且13p ＋12q ＋1r ＝4，求3p ＋2q ＋r 的最小值．【解析】(1)f 4－|x ＋32|－|x －32|≥0，根据绝对值的几何意义，得|x ＋32|＋|x －32|表示点(x,0)到－32，B 接下来找出到A ，B 距离之和为4的点．将点A 向左移动12个单位长度到点A 1(－2,0)，这时有|A 1A |＋|A 1B |＝4；同理，将点B 向右移动12个单位长度到点B 1(2,0)，这时有|B 1A |＋|B 1B |＝4.∴当x ∈[－2,2]时，|x ＋32|＋|x －32|≤4，即f 的解集为[－2,2]．(2)令a 1＝3p ，a 2＝2q ，a 3＝r ，由柯西不等式，得a 21＋a 22＋a 23)a 1＋1a 2·a 2＋1a 3·＋12q ＋p ＋2q ＋r )≥9，∵13p ＋12q ＋1r ＝4，∴3p ＋2q ＋r ≥94.上述不等式当且仅当13p ＝12q ＝1r ＝43，即p ＝14，q ＝38，r ＝34时取等号．∴3p ＋2q ＋r 的最小值为94.23．设函数f (x )＝|x ＋a |－|x －1－a |.(1)当a ＝1时，解不等式f (x )≥12；(2)若对任意a ∈[0,1]，不等式f (x )≥b 的解集不为空集，求实数b 的取值范围．【解析】(1)当a ＝1时，不等式f (x )≥12等价于|x ＋1|－|x |≥12，①当x ≤－1时，不等式化为－x －1＋x ≥12，无解；②当－1<x <0时，不等式化为x ＋1＋x ≥12，解得－14≤x <0；③当x ≥0时，不等式化为x ＋1－x ≥12，解得x ≥0.综上所述，不等式f (x )≥12的解集为－14，＋(2)∵不等式f (x )≥b 的解集不为空集，∴b ≤f (x )max ，∵f (x )＝|x ＋a |－|x －1－a |≤|x ＋a －x ＋1－a |＝|a ＋1－a |＝a ＋1－a ，当且仅当x ≥1－a 时取等号，∴f (x )max ＝a ＋1－a ，对任意a ∈[0,1]，不等式f (x )≥b 的解集不为空集，∴b ≤[a ＋1－a ]min ，令g (a )＝a ＋1－a ，∴g 2(a )＝1＋2a ·1－a ＝1＋2a (1－a )＝1＋2∵当a ∈0，12时单调递增，a ∈12，1时单调递减，当且仅当a ＝0或a ＝1，g (a )min ＝1，∴b的取值范围为(－∞，1]．。

【高中数学】数学高考《不等式选讲》试题含答案一、141．设0x >，则()2142f x x x=--的最大值为（ ） A ．24-B ．42-C ．不存在D ．52【答案】D 【解析】 【分析】化简得到()214222x xf x x ⎛⎫=-++ ⎪⎝⎭，再利用均值不等式计算得到答案. 【详解】()32221115444322222222x x x x f x x x x x ⎛⎫=--=-++≤-⋅⋅= ⎪⎝⎭当21222x x x ==即1x =时等号成立 故选：D 【点睛】本题考查了利用均值不等式求函数最值，意在考查学生对于均值不等式的灵活运用.2．已知，，则使不等式一定成立的条件是A ．B ．C ．D ．【答案】D 【解析】因为若，则，已知不等式不成立，所以，应选答案D 。

3．设|a|<1,|b|<1,则|a+b|+|a-b|与2的大小关系是 ( ) A ．|a+b|+|a-b|>2 B ．|a+b|+|a-b|<2 C ．|a+b|+|a-b|=2 D ．不能比较大小【答案】B 【解析】选B.当(a+b)(a-b)≥0时,|a+b|+|a-b|=|(a+b)+(a-b)|=2|a|<2, 当(a+b)(a-b)<0时,|a+b|+|a-b|=|(a+b)-(a-b)|=2|b|<2.4．2018年9月24日, 英国数学家M.F 阿蒂亚爵在“海德堡论坛”展示了他“证明”黎曼猜想的过程,引起数学界震动. 黎曼猜想来源于一些特殊数列求和, 记2221111.........,23S n 则（）=+++++A ．413S << B ．4332S << C ．322S << D ．2S > 【答案】C 【解析】 【分析】由题意利用不等式放缩后裂项确定S 的范围即可. 【详解】由题意可知：222111123S n =+++++L L()111123341n n >+++++⨯⨯+L L 111111123341n n ⎛⎫⎛⎫⎛⎫=+-+-++-+ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭L L 13122>+=，且222111123S n =+++++L L()111112231n n <+++++⨯⨯-⨯L L 11111112231n n L L ⎛⎫⎛⎫⎛⎫=+-+-++-+ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭122n L =-+<，综上可得：322S <<. 本题选择C 选项. 【点睛】本题的核心是考查裂项求和的方法，使用裂项法求和时，要注意正负项相消时消去了哪些项，保留了哪些项，切不可漏写未被消去的项，未被消去的项有前后对称的特点，实质上造成正负相消是此法的根源与目的．5．已知a ，b 均为正数，且20ab a b --=，则22214a b a b-+-的最小值为（ ）A ．6B ．7C ．8D ．9 【答案】B 【解析】 【分析】a ，b 均为正数，且ab ﹣a ﹣2b ＝0，可得21a b+=1，根据柯西不等式求出代数式的最小值即可． 【详解】∵a ，b 均为正数，且ab ﹣a ﹣2b ＝0， ∴21a b+=1． 则22214a b a b-+- 24a =+b 2﹣1， 又因为2a +b ＝（21a b +）（2a +b ）22b a a b=++2≥2+2＝4，当且仅当a ＝4，b ＝2时取等号．∴（24a +b 2）（1+1）≥（2a +b ）2≥16，当且仅当a ＝4，b ＝2时取等号．∴24a +b 2≥8， ∴224a a-+b 2214a b -=+b 2﹣1≥7．故选：B ． 【点睛】本题考查“乘1法”、基本不等式的性质、柯西不等式，考查了推理能力与计算能力，属于中档题．6．设n *∈N） A>BC=D ．不能确定【答案】B 【解析】 【分析】把两个代数式进行分子有理化，比较分母的大小可以比较出大小关系． 【详解】22-===.22-===.*n N ∈ 42,31n n n n +>++>+>>><<成立，因此本题选B ． 【点睛】对于二次根式的加減运算，分母有理化是常见的运算要求，但是有时分子有理化会起到意想不到的作用，尤其是在比较二个二次根式减法算式之间的大小关系时，经常会用到分子有理化这个方法．当然不等式的性质也是很重要的．7．已知2(3)f x x x =+，若1x a -≤，则下列不等式一定成立的是( ) A ．33()()f x f a a -≤+ B ．24()()f x f a a -≤+ C ．()()5f x f a a -≤+ D ．2|()()2|(1)f x f a a -≤+【答案】B 【解析】 【分析】先令a=0,排除A ，C,D,再利用绝对值三角不等式证明选项B 成立 【详解】令a=0，则1x ≤，即-1≤x≤1,()()()()()0?f x f a f x f f x -=-=≤4,此时A,C,D 不成立，下面证明选项B 成立()()22 33f x f a x x a a -=+--=()() 3x a x a -++≤()()3x a x a -++≤()3x a ++=23x a a -++≤23x a a -++≤24a +故选：B ． 【点睛】本题考查了绝对值三角不等式的应用，特值法，结合二次函数最值分析问题，准确推理计算是关键，是基础题．8．若关于x 的不等式43x x a -++<有实数解，则实数a 的取值范围是( ) A ．(7,)+∞ B ．[)7,+∞C ．(1,)+∞D ．(1,7)【答案】A 【解析】 【分析】利用绝对值的意义可求得43x x -++的最小值为7，由此可得实数a 的取值范围，得到答案. 【详解】由题意43x x -++表示数轴上的x 对应点到4和3-对应点的距离之和，其最小值为7，再由关于x 的不等式43x x a -++<有实数解，可得7a >， 即实数x 的取值范围是(7,)+∞，故选A. 【点睛】本题主要考查了绝对值的意义，以及函数绝对值不等式的有解问题，其中根据绝对值的意义，求得43x x -++的最小值为7是解得关键，着重考查了推理与运算能力，属于中档试题.9．已知函数()f x 是定义在[1,2]a a -上的偶函数,且当0x >时,()f x 单调递增，则关于x 的不等式(1)()f x f a ->的解集为 （ ） A ．45[,)33B ．2112(,][,)3333--⋃ C ．12[,)33⋃45(,]33D ．随a 的值而变化【答案】C 【解析】试题分析：∵函数()f x 是定义在[1,2]a a -上的偶函数，∴1-a=2a ，∴a=13，故函数()f x 的定义的定义域为22[,]33-，又当203x <≤时,()f x 单调递增，∴11113(1)()(1)(){23313x f x f f x f x ->->⇔->⇔-≤，解得1233x ≤<或4533x <≤，所以不等式(1)()f x f a ->的解集为12[,)33⋃45(,]33，故选C考点：本题考查了抽象函数的运用点评：此类问题往往利用偶函数的性质()()f x f x =避免了讨论，要注意灵活运用10．已知集合{|||2}A x x =≥，2{|30}B x x x =->，则A B =I ( ) A ．∅B ．{|3x x >或2}x ?C ．{|3x x >或0}x <D ．{|3x x >或0}x <【答案】B 【解析】 【分析】可以求出集合A ，B ，然后进行交集的运算即可．【详解】∵A ＝{x |x ≤﹣2，或x ≥2}，B ＝{x |x ＜0，或x ＞3}， ∴A ∩B ＝{x |x ≤﹣2，或x ＞3}． 故选：B ． 【点睛】考查描述法的定义，绝对值不等式和一元二次不等式的解法，以及交集的运算．11．已知x+3y+5z=6,则x 2+y 2+z 2的最小值为( ) A ．65B ．6 35C ．36 35D ．6【答案】C 【解析】 【分析】由题意结合柯西不等式的结论求解x 2+y 2+z 2的最小值即可. 【详解】 由柯西不等式,得：x 2+y 2+z 2=(12+32+52)(x 2+y 2+z 22221)135++≥(1×x+3×y+5×z )2135⨯=26136.3535⨯= 当且仅当x 6186,,35357y z ===时等号成立. 即x 2+y 2+z 2的最小值为3635. 本题选择C 选项. 【点睛】根据题目特征，想到利用向量方法或利用柯西不等式想法比较自然.利用柯西不等式代数形式及其向量形式解题的方法是一致的.选择哪种方法进行解题，可能会因解题者的知识解构、思维特征及对问题与方法的熟悉程度做出选择.12．设不等式3412xx a +->-对所有的[1,2]x ∈均成立,则实数a 的取值范围是（ ）A ．15a <-或47a >B ．15a <-C ．47a >或01a <<D ．15a <-或1064a <<【答案】A 【解析】 【分析】根据不等式3412xx a +->-对所有的[1,2]x ∈均成立,取2x =时,可得2431a ->,解得15a <-或47a >,利用换元法把不等式换为281t a t ->-,分47a >和15a <-两种情况讨论2()81h t t t =+-的最大值即可求得实数a 的取值范围.【详解】解:因为不等式3412x x a +->-对所有的[1,2]x ∈均成立,当2x =时,312x +-有最大值31,不等式显然要成立,即2431a ->,解得15a <-或47a >, 当[1,2]x ∈时,令2[2,4]x t =∈, 则24[4,16]xt =∈,328[16,32]x t +=∈,所以3412x x a +->-等价于281t a t ->-,①当47a >时,即281a t t ->-在[2,4]t ∈恒成立, 即281()a t t h t >+-=,即求2()81h t t t =+-的最大值,max ()(4)47h t h ==,所以47a >;②当15a <-时,281t a t ->-在[2,4]t ∈恒成立, 即281()a t t f t <-+=,即求2()81f t t t =-+的最小值,min ()(4)15f t f ==-;综上:15a <-或47a >. 故选:A 【点睛】本题考查利用二次函数的最值求绝对值不等式中的参数问题,利用换元法是关键,属于中档题.13．对任意x ∈R ,不等式22|sin ||sin |x x a a +-≥恒成立,则实数a 的取值范围是（ ） A ．01a ≤≤ B ．11a -≤≤ C ．12a -≤≤ D ．22a -≤≤【答案】B 【解析】 【分析】解法一:（换元法）设sin t x =,则原不等式可化为22||||t t a a +-≥.求函数()||||||f t t t t a =++-的最小值,从而不等式2||a a ≥可得11a -≤≤.解法二:（特殊值法）代入2a =, 1a =-,排除错误选项即可. 【详解】解:解法一:（换元法）设sin t x =,则原不等式可化为22||||t t a a +-≥.令()||||||f t t t t a =++-,则min [()](0)||f t f a ==, 从而解不等式2||a a ≥可得11a -≤≤.故选B .解法二:（特殊值法）当2a =时,因为2|sin ||sin 2|2sin 2|sin |2|sin |2x x x x x +-=-+≥+≥, 当且仅当sin 0x =时,等号成立. 此时2|sin ||sin 2|4x x +-≥不恒成立, 所以2a =不合题意,可以排除C 、D .当1a =-时,因为2|sin ||sin 1|1sin 2|sin |1|sin |1x x x x x ++=++≥+≥, 当且仅当sin 0x =时,等号成立. 此时2|sin ||sin 1|1x x ++≥恒成立, 所以1a =-符合题意,可以排除A. 故选:B 【点睛】本题考查绝对值不等式的参数问题,属于中档题,利用函数求最值的方法或者特殊值排除法都可以解题.14．函数()f x 的定义域为A ,若存在非零实数t ，使得对于任意()x C C A ∈⊆有,x t A +∈且()()f x t f x +≤，则称()f x 为C 上的t 度低调函数.已知定义域为[)0+∞，的函数()=3f x mx --，且()f x 为[)0+∞，上的6度低调函数，那么实数m 的取值范围是（ ）A ．[]0,1B ．[)1+∞，C ．(],0-∞D ．][(),01,-∞⋃+∞ 【答案】D【解析】试题分析：由题意得， ()()6633f x f x mx m mx +≤⇒+-≥-对任意0x ≥都成立.当0m ≤时， 633633|m mx m mx -≤-⇒+-≥-恒成立；当0m >时，结合图象可知，要633mx m mx +-≥-对任意0x ≥都成立，只需0x =时633mx m mx +-≥-成立即可，即6331m m -≥-⇒≥.选D.考点：1、新定义函数；2、绝对值不等式.15．设x,y,z 是互不相等的正数，则下列不等式中不恒成立的是（ ） A ．2211x x x x++≥B C ．12x y x y-+≥- D ．x y x z y z -≤-+- 【答案】C【解析】 【分析】 【详解】试题分析：x y x z z y x z z y x z y z -=-+-≤-+-=-+-，故D 恒成立； 由于函数()1f x x x=+,在(]0,1单调递减；在[)1,+∞单调递增, 当1x >时, ()()221,x x f x f x >>>即2211x x x x+>+,当01x <<,()()2201,x x f x f x <<即2211x x x x++≥正确，即A 正确；=<=,故B 恒成立，若1x y -=-,不等式12x y x y-+≥-不成立, 故C 不恒成立,故选C ． 考点：1、基本不等式证明不等式；2、单调性证明不等式及放缩法证明不等式．16．已知函数()1()02f x x a a a =-+≠．当12a <时，函数()()21g x f x x =+-有零点，则实数a 的取值范围是（ ）A ．1,02⎡⎫-⎪⎢⎣⎭B ．10,2⎡⎤⎢⎥⎣⎦C ．8,03⎡⎤-⎢⎥⎣⎦D ．4,03⎡⎤-⎢⎥⎣⎦【答案】A 【解析】 【分析】将函数的零点问题转化为方程的根问题，再构造函数1(2)g x x a x =+--求得函数的值域，可得关于a 的不等式，解不等式即可得到答案. 【详解】Q 函数()()21g x f x x =+-有零点，∴方程2112x ax a -=+--有根， 令1(2)g x x a x =+--，则31,,1()1,,2131,,2x a x a g x x a a x x a x ⎧⎪-+-≤⎪⎪=--+<≤⎨⎪⎪-->⎪⎩∴1()[,)2g x a ∈--+∞，∴11,221,2a a a ⎧-≥--⎪⎪⎨⎪<⎪⎩，解得：1,02a ⎡⎫∈-⎪⎢⎣⎭.故选：A. 【点睛】本题考查已知函数存在零点求参数的取值范围，考查函数与方程思想、转化与化归思想，考查逻辑推理能力、运算求解能力，求解时注意将函数的零点转化为方程的根.17．集合{}|12A x x =-<，1393x B x ⎧⎫=<<⎨⎬⎩⎭，则A B I 为( ) A ．()1,2 B ．()1,2-C ．()1,3D ．()1,3-【答案】B 【解析】 【分析】计算得到{}13A x x =-<<，{}12B x x =-<<，再计算A B I 得到答案. 【详解】18{}13x x =-<<，{}139123x B x x x ⎧⎫=<<=-<<⎨⎬⎩⎭， 故()1,2A B =-I . 故选：B . 【点睛】本题考查了集合的交集运算，意在考查学生的计算能力.18．已知函数()222,2log 1,2x x x f x x x ⎧-+≤=⎨->⎩，设12116n x x x ≤<<<≤L ，若()()()()()()12231n n f x f x f x f x f x f x M --+-++-≤L ，则M 的最小值为( )A ．3B ．4C ．5D ．6【答案】B 【解析】 【分析】作出函数的图象，由已知分段函数求得f （1）1=，f （2）0=，(16)3f =，等价于12231max [|()()||()()||()()|]n n M f x f x f x f x f x f x -∴≥-+-+⋯+-，再求出不等式右边的最大值即可得M 的最小值． 【详解】由222,2()log 1,2x x x f x x x ⎧-+=⎨->⎩„，得f （1）1=，f （2）0=，(16)3f =． 12116n x x x <<⋯<Q 剟，12231|()()||()()||()()|n n M f x f x f x f x f x f x -∴-+-+⋯+-…12231max[|()()||()()||()()|]n n M f x f x f x f x f x f x -∴≥-+-+⋯+-12231|()()||()()||()()||(1)(2)||(2)(16)=|10||30|4n n f x f x f x f x f x f x f f f f --+-+⋯+-≤-+--+-=∴4M ≥．则M 的最小值为4．故选：B ．【点睛】本题考查分段函数及其应用，考查三角绝对值不等式的应用，意在考查学生对这些知识的理解掌握水平．19．设x ∈R ，则“|1|1x -<”是“220x x --<”的（ ） A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件【答案】A【解析】 1111102x x x -<⇔-<-<⇔<<，22012x x x --<⇒-<<，故为充分不必要条件.20．设0x 为函数()sin f x x π=的零点，且满足001()112x f x ++<，则这样的零点有（ ）A ．18个B ．19个C ．20个D ．21个 【答案】D【解析】从题设可得00()x k x k k Z ππ=⇒=∈，又001()sin()sin()(1)222k f x x k ππππ+=+=+=-，故(1)11k k +-<，当k 取奇数时，12k <，则1,3,5,7,9,11k =±±±±±±，共12个数；当k 取偶数时，10k <，则0,2,4,6,8k =±±±±，共9个数，所以这样的零点的个数共有21个，应选答案D 。

2019年新课标全国卷（1、2、3卷）理科数学备考宝典15．不等式选讲一、考试大纲1．理解绝对值的几何意义,并能利用含绝对值不等式的几何意义证明以下不等式：（1）a b a b +≤+ （2）a b a c c b -≤-+-（3）会利用绝对值的几何意义求解以下类型的不等式：ax b c +≤；ax b c +≥；x a x b c -+-≥2．了解下列柯西不等式的几种不同形式,理解它们的几何意义,并会证明.（1）a b a b ⋅≥⋅；（2）22222()()()a b c d ac bd ++≥+；（3≥(此不等式通常称为平面三角不等式.) 3．会用参数配方法讨论柯西不等式的一般情形：222111()n nni ii i i i i a ba b ===⋅≥∑∑∑4．会用向量递归方法讨论排序不等式.5．了解数学归纳法的原理及其使用范围,会用数学归纳法证明一些简单问题. 6．会用数学归纳法证明伯努利不等式：(1)1n x nx +>+ (1x >-，0x ≠，n 为大于1的正整数)，了解当n 为大于1的实数时伯努利不等式也成立.7．会用上述不等式证明一些简单问题.能够利用平均值不等式、柯西不等式求一些特定函数的极值. 8．了解证明不等式的基本方法：比较法、综合法、分析法、反证法、放缩法.二、新课标全国卷命题分析不等式选讲部分主要以考查以考查绝对值不等式的解法为主，偶尔也考查不等式证明的方法，经常与函数结合，考查数形结合和转化与化归思想是，考查去绝对值的方法是试题变化中不变的规律，基本不等式是考查不等式证明方法的主要依据；在求解过程中考查绝对值三角不等式的灵活应用能力。

分析问题的方法是不等式证明的关键，关于不等式证明的方法，没有具体的知识点，只有方法要求，因此它的载体丰富多彩. 三、典型高考试题讲评题型1 绝对值不等式的解法与恒成立问题例1 （2018·新课标I 卷，23）已知()11f x x ax =+--.（I ）当1a =时，求不等式()1f x >的解集；（II ）若()0,1x ∈时不等式()f x x >成立，求a 的取值范围. 解析：（I ）依题意，111x x +-->，该不等式等价于1,111,x x x <-⎧⎨--+->⎩11,111,x x x -≤≤⎧⎨++->⎩或1,111,x x x >⎧⎨+-+>⎩解得12x >，即等式()1f x >的解集为12x x ⎧⎫>⎨⎬⎩⎭； （II ）依题意，11x ax x +-->；当()0,1x ∈时，该式化为 11x ax x +-->，即11ax -<，即111ax -<-<，即02ax <<，故0,2,ax ax >⎧⎨<⎩在()0,1上恒成立，故02a <≤，即a 的取值范围为(]0,2.【解题技巧】形如||||x a x b c -+-≥(或c ≤)型的不等式主要有两种解法：(1)分段讨论法：利用绝对值号内式子对应方程的根，将数轴分为(,]a -∞，(,]a b ，(,)b +∞ (此处设a b <)三个部分，将每部分去掉绝对值号并分别列出对应的不等式求解，然后取各个不等式解集的并集；(2)图像法：作出函数1||||y x a x b =-+-和2y c =的图像，结合图像求解. 不等式的恒成立问题是高考的重难点，此类问题一般有两种解法： （1）利用函数思想转化为函数的最值问题进行分析；（2）通过数形结合构造出两个函数，通过寻找临界状态得到参数的取值范围.题型2 证明不等式例2 （2017·新课标Ⅱ，23）已知330,0,2a b a b >>+=，证明：（1）33()()4a b a b ++≥；（2）2a b +≤． 解析：（1）解法一：由柯西不等式得：55222222332()()))()4a b a b a b a b ⎡⎤⎡⎤++=+⋅+≥+=⎣⎦⎣⎦解法二：5566553325533()()()2a b a b a b ab a b a b ab a b a b ++=+++=+++-33233332()2()4a b a b a b ≥++=+=解法三：()()()()()2555533553342a b a b a b a b a b ab a b a b ++-=++-+=+-又0,0a b >>，所以()255332220ab a b a b ab a b+-=-≥．当a b =时，等号成立．所以，()()5540a b a b ++-≥，即55()()4a b a b ++≥．（2）解法一：由332a b +=及2()4a b ab +≤得2222()()()()3a b a b ab a b a b ab ⎡⎤=+⋅+-=+⋅+-⎣⎦2323()()()()44a b a b a b a b ⎡⎤++≥+⋅+-=⎢⎥⎣⎦所以2a b +≤．解法二：（反证法）假设2a b +>，则2a b >-，两边同时立方得：3323(2)8126a b b b b >-=-+-，即3328126a b b b +>-+，因为332a b +=，所以261260b b -+<，即26(1)0b -<，矛盾，所以假设不成立，即2a b +≤． 解法三：因为332a b +=，所以：()()()3333322333843344a b a b a b a a b ab b a b +-=+-+=+++--()()()()222333a b a b a b a b a b =-+-=-+-.又0,0a b >>，所以: ()()230a b a b -+-≤，所以，()38a b +≤，即2a b +≤．解法四：因为33113,113a a b b ++≥=++≥=，所以3311113()a b a b +++++≥+，即63()a b ≥+，即2a b +≤（当且仅当1a b ==时取等号）． 【解题技巧】利用基本不等式证明不等式是综合法证明不等式的一种情况，证明思路是从已知不等式和问题的已知条件出发，借助不等式的性质和有关定理，经过逐步的逻辑推理最后转化为需证问题，若不等式恒等变形之后与二次函数有关，可用配方法。

2010不等式选讲1（2010·辽宁高考理科·Ｔ24）已知c b a ,,均为正数，证明：36)111(2222≥+++++c b a c b a ， 并确定c b a ,,为何值时，等号成立。

【命题立意】本题考查了不等式的性质，考查了均值不等式。

【思路点拨】把222111a b c a b c++++分别用均值不等式，相加后，再用均值不等式。

【规范解答】（证法一）∵,,a b c 均为正数，由均值不等式得 222233()a b c abc ++≥…………………………①131113()abc a b c-++≥， ∴223111()9()abc a b c-++≥……………………② 22222233111()3()9()a b c abc abc a b c -∴+++++≥+ 22333()9()22763abc abc -+≥=又……………………③ ∴原不等式成立。

当且仅当a=b=c 时，①式和②式等号成立，当且仅当22333()9()abc abc -=时，③式等号成立。

即当a=b=c ＝143时原式等号成立。

（证法二）∵a,b,c 都是正数，由基本不等式得 222222222a b abb c bc c a ac+≥+≥+≥ ∴222a b c ab bc ac ++≥++………………………………① 同理111111a b c ab bc ac++≥++………………………………② ∴2222111()111333a b c a b c ab bc ac ab bc ac+++++≥+++++63≥…………………………………………③∴原不等式成立当且仅当a=b=c 时，①式和②式等号成立，当且仅当a=b=c,222()()()3ab bc ac ===时，③式等号成立。

即当a=b=c ＝143时原式等号成立。

2.（2010·福建高考理科·Ｔ21）已知函数f (x )=x a -．(Ⅰ)若不等式f (x )≤3的解集为｛x -1≤x ≤5｝，求实数a 的值；(Ⅱ)在(Ⅰ)的条件下，若f (x )+f (5x +)≥m 对一切实数x 恒成立，求实数m 的取值范围。

高考数学真题精选（按考点分类）专题52 不等式选讲（学生版）1．（2019•新课标Ⅱ）已知f（x）＝|x﹣a|x+|x﹣2|（x﹣a）．（1）当a＝1时，求不等式f（x）＜0的解集；（2）当x∈（﹣∞，1）时，f（x）＜0，求a的取值范围．2．（2018•新课标Ⅰ）已知f（x）＝|x+1|﹣|ax﹣1|．（1）当a＝1时，求不等式f（x）＞1的解集；（2）若x∈（0，1）时不等式f（x）＞x成立，求a的取值范围．3．（2018•新课标Ⅱ）设函数f（x）＝5﹣|x+a|﹣|x﹣2|．（1）当a＝1时，求不等式f（x）≥0的解集；（2）若f（x）≤1，求a的取值范围．4．（2017•新课标Ⅰ）已知函数f（x）＝﹣x2+ax+4，g（x）＝|x+1|+|x﹣1|．（1）当a＝1时，求不等式f（x）≥g（x）的解集；（2）若不等式f（x）≥g（x）的解集包含[﹣1，1]，求a的取值范围．5．（2017•新课标Ⅲ）已知函数f（x）＝|x+1|﹣|x﹣2|．（1）求不等式f（x）≥1的解集；（2）若不等式f（x）≥x2﹣x+m的解集非空，求m的取值范围．6．（2016•新课标Ⅲ）已知函数f（x）＝|2x﹣a|+a．（1）当a＝2时，求不等式f（x）≤6的解集；（2）设函数g（x）＝|2x﹣1|，当x∈R时，f（x）+g（x）≥3，求a的取值范围．7．（2016•新课标Ⅱ）已知函数f（x）＝|x−12|+|x+12|，M为不等式f（x）＜2的解集．（Ⅰ）求M；（Ⅱ）证明：当a，b∈M时，|a+b|＜|1+ab|．8．（2015•新课标Ⅰ）已知函数f（x）＝|x+1|﹣2|x﹣a|，a＞0．（Ⅰ）当a＝1时，求不等式f（x）＞1的解集；（Ⅱ）若f（x）的图象与x轴围成的三角形面积大于6，求a的取值范围．9．（2014•新课标Ⅱ）设函数f（x）＝|x+1a|+|x﹣a|（a＞0）．（Ⅰ）证明：f（x）≥2；（Ⅱ）若f （3）＜5，求a 的取值范围． 10．（2014•新课标Ⅰ）若a ＞0，b ＞0，且1a +1b=√ab ．（Ⅰ）求a 3+b 3的最小值；（Ⅱ）是否存在a ，b ，使得2a +3b ＝6？并说明理由．11．（2013•新课标Ⅰ）已知函数f （x ）＝|2x ﹣1|+|2x +a |，g （x ）＝x +3． （Ⅰ）当a ＝﹣2时，求不等式f （x ）＜g （x ）的解集；（Ⅱ）设a ＞﹣1，且当x ∈[−a2，12]时，f （x ）≤g （x ），求a 的取值范围．12．（2011•辽宁）选修4﹣5：不等式选讲 已知函数f （x ）＝|x ﹣2|﹣|x ﹣5|． （1）证明：﹣3≤f （x ）≤3；（2）求不等式f （x ）≥x 2﹣8x +15的解集． 13．（2019•新课标Ⅲ）设x ，y ，z ∈R ，且x +y +z ＝1． （1）求（x ﹣1）2+（y +1）2+（z +1）2的最小值；（2）若（x ﹣2）2+（y ﹣1）2+（z ﹣a ）2≥13成立，证明：a ≤﹣3或a ≥﹣1． 14．（2019•新课标Ⅰ）已知a ，b ，c 为正数，且满足abc ＝1．证明： （1）1a +1b+1c≤a 2+b 2+c 2；（2）（a +b ）3+（b +c ）3+（c +a ）3≥24．15．（2017•新课标Ⅱ）已知a ＞0，b ＞0，a 3+b 3＝2．证明： （1）（a +b ）（a 5+b 5）≥4； （2）a +b ≤2．16．（2015•新课标Ⅱ）设a ，b ，c ，d 均为正数，且a +b ＝c +d ，证明： （1）若ab ＞cd ，则√a +√b ＞√c +√d ；（2）√a +√b ＞√c +√d 是|a ﹣b |＜|c ﹣d |的充要条件． 17．（2013•辽宁）（1）证明：当x ∈[0，1]时，√22x ≤sinx ≤x ； （2）若不等式ax +x 2+x 32+2(x +2)cosx ≤4对x ∈[0，1]恒成立，求实数a 的取值范围．18．（2013•新课标Ⅱ）【选修4﹣﹣5；不等式选讲】 设a ，b ，c 均为正数，且a +b +c ＝1，证明：（Ⅰ）ab +bc +ca ≤13（Ⅱ）a 2b+b 2c+c 2a≥1．历年高考数学真题精选（按考点分类）专题52 不等式选讲（学生版）一．解答题（共18小题）1．（2019•新课标Ⅱ）已知f （x ）＝|x ﹣a |x +|x ﹣2|（x ﹣a ）． （1）当a ＝1时，求不等式f （x ）＜0的解集；（2）当x ∈（﹣∞，1）时，f （x ）＜0，求a 的取值范围． 解：（1）当a ＝1时，f （x ）＝|x ﹣1|x +|x ﹣2|（x ﹣1），∵f （x ）＜0，∴当x ＜1时，f （x ）＝﹣2（x ﹣1）2＜0，恒成立，∴x ＜1； 当x ≥1时，f （x ）＝（x ﹣1）（x +|x ﹣2|）≥0恒成立，∴x ∈∅； 综上，不等式的解集为（﹣∞，1）；（2）当a ≥1时，f （x ）＝2（a ﹣x ）（x ﹣1）＜0在x ∈（﹣∞，1）上恒成立； 当a ＜1时，x ∈（a ，1），f （x ）＝2（x ﹣a ）＞0，不满足题意， ∴a 的取值范围为：[1，+∞）2．（2018•新课标Ⅰ）已知f （x ）＝|x +1|﹣|ax ﹣1|． （1）当a ＝1时，求不等式f （x ）＞1的解集；（2）若x ∈（0，1）时不等式f （x ）＞x 成立，求a 的取值范围．解：（1）当a ＝1时，f （x ）＝|x +1|﹣|x ﹣1|={2，x ＞12x ，−1≤x ≤1−2，x ＜−1，由f （x ）＞1，∴{2x ＞1−1≤x ≤1或{2＞1x ＞1， 解得x ＞12，故不等式f （x ）＞1的解集为（12，+∞），（2）当x ∈（0，1）时不等式f （x ）＞x 成立， ∴|x +1|﹣|ax ﹣1|﹣x ＞0， 即x +1﹣|ax ﹣1|﹣x ＞0， 即|ax ﹣1|＜1，∴﹣1＜ax﹣1＜1，∴0＜ax＜2，∵x∈（0，1），∴a＞0，∴0＜x＜2 a，∴a＜2 x∵2x＞2，∴0＜a≤2，故a的取值范围为（0，2]．3．（2018•新课标Ⅱ）设函数f（x）＝5﹣|x+a|﹣|x﹣2|．（1）当a＝1时，求不等式f（x）≥0的解集；（2）若f（x）≤1，求a的取值范围．解：（1）当a＝1时，f（x）＝5﹣|x+1|﹣|x﹣2|={2x+4，x≤−1 2，−1＜x＜2−2x+6，x≥2．当x≤﹣1时，f（x）＝2x+4≥0，解得﹣2≤x≤﹣1，当﹣1＜x＜2时，f（x）＝2≥0恒成立，即﹣1＜x＜2，当x≥2时，f（x）＝﹣2x+6≥0，解得2≤x≤3，综上所述不等式f（x）≥0的解集为[﹣2，3]，（2）∵f（x）≤1，∴5﹣|x+a|﹣|x﹣2|≤1，∴|x+a|+|x﹣2|≥4，∴|x+a|+|x﹣2|＝|x+a|+|2﹣x|≥|x+a+2﹣x|＝|a+2|，∴|a+2|≥4，解得a≤﹣6或a≥2，故a的取值范围（﹣∞，﹣6]∪[2，+∞）．4．（2017•新课标Ⅰ）已知函数f（x）＝﹣x2+ax+4，g（x）＝|x+1|+|x﹣1|．（1）当a＝1时，求不等式f（x）≥g（x）的解集；（2）若不等式f（x）≥g（x）的解集包含[﹣1，1]，求a的取值范围．解：（1）当a ＝1时，f （x ）＝﹣x 2+x +4，是开口向下，对称轴为x =12的二次函数，g （x ）＝|x +1|+|x ﹣1|={2x ，x ＞12，−1≤x ≤1−2x ，x ＜−1，当x ∈（1，+∞）时，令﹣x 2+x +4＝2x ，解得x =√17−12，g （x ）在（1，+∞）上单调递增，f （x ）在（1，+∞）上单调递减，∴此时f （x ）≥g （x ）的解集为（1，√17−12]； 当x ∈[﹣1，1]时，g （x ）＝2，f （x ）≥f （﹣1）＝2．当x ∈（﹣∞，﹣1）时，g （x ）单调递减，f （x ）单调递增，且g （﹣1）＝f （﹣1）＝2． 综上所述，f （x ）≥g （x ）的解集为[﹣1，√17−12]； （2）依题意得：﹣x 2+ax +4≥2在[﹣1，1]恒成立，即x 2﹣ax ﹣2≤0在[﹣1，1]恒成立，则只需{12−a ⋅1−2≤0(−1)2−a(−1)−2≤0，解得﹣1≤a ≤1，故a 的取值范围是[﹣1，1]．5．（2017•新课标Ⅲ）已知函数f （x ）＝|x +1|﹣|x ﹣2|． （1）求不等式f （x ）≥1的解集；（2）若不等式f （x ）≥x 2﹣x +m 的解集非空，求m 的取值范围．解：（1）∵f （x ）＝|x +1|﹣|x ﹣2|={−3，x ＜−12x −1，−1≤x ≤23，x ＞2，f （x ）≥1，∴当﹣1≤x ≤2时，2x ﹣1≥1，解得1≤x ≤2； 当x ＞2时，3≥1恒成立，故x ＞2； 综上，不等式f （x ）≥1的解集为{x |x ≥1}．（2）原式等价于存在x ∈R 使得f （x ）﹣x 2+x ≥m 成立， 即m ≤[f （x ）﹣x 2+x ]max ，设g （x ）＝f （x ）﹣x 2+x ．由（1）知，g （x ）={−x 2+x −3，x ≤−1−x 2+3x −1，−1＜x ＜2−x 2+x +3，x ≥2，当x ≤﹣1时，g （x ）＝﹣x 2+x ﹣3，其开口向下，对称轴方程为x =12＞−1， ∴g （x ）≤g （﹣1）＝﹣1﹣1﹣3＝﹣5；当﹣1＜x ＜2时，g （x ）＝﹣x 2+3x ﹣1，其开口向下，对称轴方程为x =32∈（﹣1，2）， ∴g （x ）≤g （32）=−94+92−1=54；当x ≥2时，g （x ）＝﹣x 2+x +3，其开口向下，对称轴方程为x =12＜2， ∴g （x ）≤g （2）＝﹣4+2+3＝1； 综上，g （x ）max =54，∴m 的取值范围为（﹣∞，54]．6．（2016•新课标Ⅲ）已知函数f （x ）＝|2x ﹣a |+a ． （1）当a ＝2时，求不等式f （x ）≤6的解集；（2）设函数g （x ）＝|2x ﹣1|，当x ∈R 时，f （x ）+g （x ）≥3，求a 的取值范围． 解：（1）当a ＝2时，f （x ）＝|2x ﹣2|+2， ∵f （x ）≤6，∴|2x ﹣2|+2≤6， |2x ﹣2|≤4，|x ﹣1|≤2， ∴﹣2≤x ﹣1≤2， 解得﹣1≤x ≤3，∴不等式f （x ）≤6的解集为{x |﹣1≤x ≤3}． （2）∵g （x ）＝|2x ﹣1|，∴f （x ）+g （x ）＝|2x ﹣1|+|2x ﹣a |+a ≥3， 2|x −12|+2|x −a 2|+a ≥3， |x −12|+|x −a 2|≥3−a2， 当a ≥3时，成立，当a ＜3时，|x −12|+|x −a 2|≥12|a ﹣1|≥3−a2＞0， ∴（a ﹣1）2≥（3﹣a ）2， 解得2≤a ＜3，∴a 的取值范围是[2，+∞）．7．（2016•新课标Ⅱ）已知函数f （x ）＝|x −12|+|x +12|，M 为不等式f （x ）＜2的解集． （Ⅰ）求M ；（Ⅱ）证明：当a ，b ∈M 时，|a +b |＜|1+ab |．解：（I ）当x ＜−12时，不等式f （x ）＜2可化为：12−x ﹣x −12＜2，解得：x ＞﹣1， ∴﹣1＜x ＜−12，当−12≤x ≤12时，不等式f （x ）＜2可化为：12−x +x +12=1＜2，此时不等式恒成立， ∴−12≤x ≤12，当x ＞12时，不等式f （x ）＜2可化为：−12+x +x +12＜2， 解得：x ＜1， ∴12＜x ＜1，综上可得：M ＝（﹣1，1）； 证明：（Ⅱ）当a ，b ∈M 时， （a 2﹣1）（b 2﹣1）＞0， 即a 2b 2+1＞a 2+b 2，即a 2b 2+1+2ab ＞a 2+b 2+2ab ， 即（ab +1）2＞（a +b ）2， 即|a +b |＜|1+ab |．8．（2015•新课标Ⅰ）已知函数f （x ）＝|x +1|﹣2|x ﹣a |，a ＞0． （Ⅰ）当a ＝1时，求不等式f （x ）＞1的解集；（Ⅱ）若f （x ）的图象与x 轴围成的三角形面积大于6，求a 的取值范围． 解：（Ⅰ）当a ＝1时，不等式f （x ）＞1，即|x +1|﹣2|x ﹣1|＞1， 即{x ＜−1−x −1−2(1−x)＞1①，或{−1≤x ＜1x +1−2(1−x)＞1②，或{x ≥1x +1−2(x −1)＞1③． 解①求得x ∈∅，解②求得23＜x ＜1，解③求得1≤x ＜2．综上可得，原不等式的解集为（23，2）．（Ⅱ）函数f （x ）＝|x +1|﹣2|x ﹣a |={x −1−2a ，x ＜−13x +1−2a ，−1≤x ≤a −x +1+2a ，x ＞a，由此求得f （x ）的图象与x 轴的交点A （2a−13，0），B （2a +1，0），故f （x ）的图象与x 轴围成的三角形的第三个顶点C （a ，a +1）， 由△ABC 的面积大于6， 可得12[2a +1−2a−13]•（a +1）＞6，求得a ＞2． 故要求的a 的范围为（2，+∞）．9．（2014•新课标Ⅱ）设函数f （x ）＝|x +1a |+|x ﹣a |（a ＞0）． （Ⅰ）证明：f （x ）≥2；（Ⅱ）若f （3）＜5，求a 的取值范围．解：（Ⅰ）证明：∵a ＞0，f （x ）＝|x +1a |+|x ﹣a |≥|（x +1a ）﹣（x ﹣a ）|＝|a +1a |＝a +1a ≥2√a ⋅1a =2， 故不等式f （x ）≥2成立． （Ⅱ）∵f （3）＝|3+1a |+|3﹣a |＜5，∴当a ＞3时，不等式即a +1a＜5，即a 2﹣5a +1＜0，解得3＜a ＜5+√212． 当0＜a ≤3时，不等式即 6﹣a +1a ＜5，即 a 2﹣a ﹣1＞0，求得1+√52＜a ≤3． 综上可得，a 的取值范围（1+√52，5+√212）．10．（2014•新课标Ⅰ）若a ＞0，b ＞0，且1a+1b=√ab ．（Ⅰ）求a 3+b 3的最小值；（Ⅱ）是否存在a ，b ，使得2a +3b ＝6？并说明理由． 解：（Ⅰ）∵a ＞0，b ＞0，且1a+1b=√ab ，∴√ab =1a +1b ≥2√1ab ，∴ab ≥2， 当且仅当a ＝b =√2时取等号．∵a 3+b 3 ≥2√(ab)3≥2√23=4√2，当且仅当a ＝b =√2时取等号， ∴a 3+b 3的最小值为4√2．（Ⅱ）∵2a +3b ≥2√2a ⋅3b =2√6ab ，当且仅当2a ＝3b 时，取等号． 而由（1）可知，2√6ab ≥2√12=4√3＞6， 故不存在a ，b ，使得2a +3b ＝6成立．11．（2013•新课标Ⅰ）已知函数f （x ）＝|2x ﹣1|+|2x +a |，g （x ）＝x +3． （Ⅰ）当a ＝﹣2时，求不等式f （x ）＜g （x ）的解集；（Ⅱ）设a ＞﹣1，且当x ∈[−a 2，12]时，f （x ）≤g （x ），求a 的取值范围．解：（Ⅰ）当a ＝﹣2时，求不等式f （x ）＜g （x ）化为|2x ﹣1|+|2x ﹣2|﹣x ﹣3＜0． 设y ＝|2x ﹣1|+|2x ﹣2|﹣x ﹣3，则y ={−5x ，x ＜12−x −2，12≤x ≤13x −6，x ＞1，它的图象如图所示：结合图象可得，y ＜0的解集为（0，2），故原不等式的解集为（0，2）． （Ⅱ）设a ＞﹣1，且当x ∈[−a2，12]时，f （x ）＝1+a ，不等式化为1+a ≤x +3，故x ≥a ﹣2对x ∈[−a 2，12]都成立．故−a 2≥a ﹣2， 解得a ≤43，故a 的取值范围为（﹣1，43]．12．（2011•辽宁）选修4﹣5：不等式选讲已知函数f （x ）＝|x ﹣2|﹣|x ﹣5|．（1）证明：﹣3≤f （x ）≤3；（2）求不等式f （x ）≥x 2﹣8x +15的解集．解：（1）f （x ）＝|x ﹣2|﹣|x ﹣5|={−3，x ≤22x −7，2＜x ＜53，x ≥5．当2＜x ＜5时，﹣3＜2x ﹣7＜3．所以﹣3≤f （x ）≤3．（2）由（1）可知，当x ≤2时，f （x ）≥x 2﹣8x +15的解集为空集；当2＜x ＜5时，f （x ）≥x 2﹣8x +15的解集为{x |5−√3≤x ＜5}；当x ≥5时，f （x ）≥x 2﹣8x +15的解集为{x |5≤x ≤6}．综上，不等式f （x ）≥x 2﹣8x +15的解集为{x |5−√3≤x ≤6}．13．（2019•新课标Ⅲ）设x ，y ，z ∈R ，且x +y +z ＝1．（1）求（x ﹣1）2+（y +1）2+（z +1）2的最小值；（2）若（x ﹣2）2+（y ﹣1）2+（z ﹣a ）2≥13成立，证明：a ≤﹣3或a ≥﹣1．解：（1）x ，y ，z ∈R ，且x +y +z ＝1，由柯西不等式可得（12+12+12）[（x ﹣1）2+（y +1）2+（z +1）2]≥（x ﹣1+y +1+z +1）2＝4，可得（x ﹣1）2+（y +1）2+（z +1）2≥43，即有（x ﹣1）2+（y +1）2+（z +1）2的最小值为43； （2）证明：由x +y +z ＝1，柯西不等式可得（12+12+12）[（x ﹣2）2+（y ﹣1）2+（z ﹣a ）2]≥（x ﹣2+y ﹣1+z ﹣a ）2＝（a +2）2，可得（x ﹣2）2+（y ﹣1）2+（z ﹣a ）2≥(a+2)23， 即有（x ﹣2）2+（y ﹣1）2+（z ﹣a ）2的最小值为(a+2)23， 由题意可得(a+2)23≥13， 解得a ≥﹣1或a ≤﹣3．14．（2019•新课标Ⅰ）已知a ，b ，c 为正数，且满足abc ＝1．证明：（1）1a +1b +1c ≤a 2+b 2+c 2；（2）（a +b ）3+（b +c ）3+（c +a ）3≥24．证明：（1）分析法：已知a ，b ，c 为正数，且满足abc ＝1．要证（1）1a +1b +1c ≤a 2+b 2+c 2；因为abc ＝1．就要证：abc a +abc b +abc c ≤a 2+b 2+c 2；即证：bc +ac +ab ≤a 2+b 2+c 2；即：2bc +2ac +2ab ≤2a 2+2b 2+2c 2；2a 2+2b 2+2c 2﹣2bc ﹣2ac ﹣2ab ≥0（a ﹣b ）2+（a ﹣c ）2+（b ﹣c ）2≥0；∵a ，b ，c 为正数，且满足abc ＝1．∴（a ﹣b ）2≥0；（a ﹣c ）2≥0；（b ﹣c ）2≥0恒成立；当且仅当：a ＝b ＝c ＝1时取等号． 即（a ﹣b ）2+（a ﹣c ）2+（b ﹣c ）2≥0得证．故1a +1b +1c ≤a 2+b 2+c 2得证．（2）证（a +b ）3+（b +c ）3+（c +a ）3≥24成立；即：已知a ，b ，c 为正数，且满足abc ＝1．（a +b ）为正数；（b +c ）为正数；（c +a ）为正数；（a +b ）3+（b +c ）3+（c +a ）3≥3（a +b ）•（b +c ）•（c +a ）；当且仅当（a +b ）＝（b +c ）＝（c +a ）时取等号；即：a ＝b ＝c ＝1时取等号； ∵a ，b ，c 为正数，且满足abc ＝1．（a +b ）≥2√ab ；（b +c ）≥2√bc ；（c +a ）≥2√ac ；当且仅当a ＝b ，b ＝c ；c ＝a 时取等号；即：a ＝b ＝c ＝1时取等号；∴（a +b ）3+（b +c ）3+（c +a ）3≥3（a +b ）•（b +c ）•（c +a ）≥3×8√ab •√bc •√ac =24abc ＝24；当且仅当a ＝b ＝c ＝1时取等号；故（a +b ）3+（b +c ）3+（c +a ）3≥24．得证．故得证．15．（2017•新课标Ⅱ）已知a ＞0，b ＞0，a 3+b 3＝2．证明：（1）（a +b ）（a 5+b 5）≥4；（2）a +b ≤2．证明：（1）由柯西不等式得：（a +b ）（a 5+b 5）≥（√a ⋅a 5+√b ⋅b 5）2＝（a 3+b 3）2≥4， 当且仅当√ab 5=√ba 5，即a ＝b ＝1时取等号，（2）∵a 3+b 3＝2，∴（a +b ）（a 2﹣ab +b 2）＝2，∴（a +b ）[（a +b ）2﹣3ab ]＝2，∴（a +b ）3﹣3ab （a +b ）＝2，∴(a+b)3−23(a+b)=ab ，由均值不等式可得：(a+b)3−23(a+b)=ab ≤（a+b 2）2， ∴（a +b ）3﹣2≤3(a+b)34， ∴14（a +b ）3≤2， ∴a +b ≤2，当且仅当a ＝b ＝1时等号成立．16．（2015•新课标Ⅱ）设a ，b ，c ，d 均为正数，且a +b ＝c +d ，证明：（1）若ab ＞cd ，则√a +√b ＞√c +√d ；（2）√a +√b ＞√c +√d 是|a ﹣b |＜|c ﹣d |的充要条件．证明：（1）由于（√a +√b ）2＝a +b +2√ab ，（√c +√d ）2＝c +d +2√cd ，由a ，b ，c ，d 均为正数，且a +b ＝c +d ，ab ＞cd ，则√ab ＞√cd ，即有（√a +√b ）2＞（√c +√d ）2，则√a +√b ＞√c +√d ；（2）①若√a +√b ＞√c +√d ，则（√a +√b ）2＞（√c +√d ）2，即为a +b +2√ab ＞c +d +2√cd ，由a +b ＝c +d ，则ab ＞cd ，于是（a ﹣b ）2＝（a +b ）2﹣4ab ，（c ﹣d ）2＝（c +d ）2﹣4cd ，即有（a ﹣b ）2＜（c ﹣d ）2，即为|a ﹣b |＜|c ﹣d |；②若|a ﹣b |＜|c ﹣d |，则（a ﹣b ）2＜（c ﹣d ）2，即有（a +b ）2﹣4ab ＜（c +d ）2﹣4cd ，由a +b ＝c +d ，则ab ＞cd ，则有（√a +√b ）2＞（√c +√d ）2．综上可得，√a +√b ＞√c +√d 是|a ﹣b |＜|c ﹣d |的充要条件．17．（2013•辽宁）（1）证明：当x ∈[0，1]时，√22x ≤sinx ≤x ； （2）若不等式ax +x 2+x 32+2(x +2)cosx ≤4对x ∈[0，1]恒成立，求实数a 的取值范围． （1）证明：记F （x ）＝sin x −√22x ，则F ′（x ）＝cos x −√22． 当x ∈（0，π4）时，F ′（x ）＞0，F （x ）在[0，π4]上是增函数；当x ∈（π4，1）时，F ′（x ）＜0，F （x ）在[π4，1]上是减函数； 又F （0）＝0，F （1）＞0，所以当x ∈[0，1]时，F （x ）≥0，即sin x ≥√22x ，记H （x ）＝sin x ﹣x ，则当x ∈（0，1）时，H ′（x ）＝cos x ﹣1＜0，所以H （x ）在[0，1]上是减函数；则H （x ）≤H （0）＝0，即sin x ≤x ．综上，√22x ≤sin x ≤x ． （2）∵当x ∈[0，1]时，ax +x 2+x 32+2（x +2）cos x ﹣4＝（a +2）x +x 2+x 32−4（x +2）sin 2x 2≤（a +2）x +x 2+x 32−4（x +2）(√24x)2＝（a +2）x ，∴当a ≤﹣2时，不等式ax +x 2+x 32+2（x +2）cos x ≤4对x ∈[0，1]恒成立，下面证明，当a ＞﹣2时，不等式ax +x 2+x 32+2（x +2）cos x ≤4对x ∈[0，1]不恒成立． ∵当x ∈[0，1]时，ax +x 2+x 32+2（x +2）cos x ﹣4＝（a +2）x +x 2+x 32−4（x +2）sin 2x 2≥（a +2）x +x 2+x 32−4（x +2）(x 2)2＝（a +2）x ﹣x 2−x 32≥（a +2）x −32x 2=−32x [x −23（a +2）]．所以存在x 0∈（0，1）（例如x 0取a+23和12中的较小值）满足ax 0+x 02+x032+2（x 0+2）cos x 0﹣4＞0，即当a ＞﹣2时，不等式ax +x 2+x 32+2（x +2）cos x ≤4对x ∈[0，1]不恒成立．综上，实数a 的取值范围是（﹣∞，﹣2]．18．（2013•新课标Ⅱ）【选修4﹣﹣5；不等式选讲】设a ，b ，c 均为正数，且a +b +c ＝1，证明：（Ⅰ）ab +bc +ca ≤13（Ⅱ）a 2b +b2c +c 2a ≥1．证明：（Ⅰ）由a 2+b 2≥2ab ，b 2+c 2≥2bc ，c 2+a 2≥2ca 得a 2+b 2+c 2≥ab +bc +ca ， 由题设得（a +b +c ）2＝1，即a 2+b 2+c 2+2ab +2bc +2ca ＝1，所以3（ab +bc +ca ）≤1，即ab +bc +ca ≤13．（Ⅱ）因为a2b +b ≥2a ，b2c +c ≥2b ，c 2a +a ≥2c ，故a 2b +b 2c +c2a +（a +b +c ）≥2（a +b +c ），即a 2b +b2c +c 2a ≥a +b +c ．所以a 2b +b 2c +c 2a ≥1．。

第三节 不等式选讲高考试题考点一 含绝对值不等式的解法1.(2013年重庆卷,理16)若关于实数x 的不等式|x-5|+|x+3|<a 无解,则实数a 的取值范围是 .解析:法一 ∵|x-5|+|x+3|=22,5,8,35,22,5,x x x x x -⎧⎪-⎨⎪-+-⎩＞＜＜＜ ∴|x-5|+|x+3|≥8,当a ≤8时不等式无解.法二 ∵|x-5|+|x+3|≥|(x-5)-(x+3)|=8,∴当a ≤8时,不等式无解.答案:(-∞,8]2.(2013年陕西卷,理15A)(不等式选做题)已知a,b,m,n 均为正数,且a+b=1,mn=2,则(am+bn)(bm+an)的最小值为 .解析:(am+bn)(bm+an)=ab(m 2+n 2)+(a 2+b 2)mn=ab(m 2+n 2)+2[(a+b)2-2ab]≥2mnab+2(1-2ab)=2,当且仅当.答案:23.(2011年陕西卷,理15)若关于x 的不等式|a|≥|x+1|+|x-2|存在实数解,则实数a 的取值范围是 . 解析:因为|x+1|+|x-2|=|x+1|+|2-x|≥|x+1+2-x|=3,所以|a|≥|x+1|+|x-2|有解时,|a|≥3,解得a ≤-3或a ≥3.答案:(-∞,-3]∪[3,+∞)4.(2013年新课标全国卷Ⅰ,理24)已知函数f(x)=|2x-1|+|2x+a|,g(x)=x+3.(1)当a=-2时,求不等式f(x)<g(x)的解集;(2)设a>-1,且当x ∈[-2a ,12）时,f(x)≤g(x),求a 的取值范围. 解:(1)当a=-2时,不等式f(x)<g(x)化为|2x-1|+|2x-2|-x-3<0.设函数y=|2x-1|+|2x-2|-x-3,则y=15,,212,1,236, 1.x x x x x x ⎧-⎪⎪⎪--⎨⎪⎪-⎪⎩＜≤≤＞ 其图象如图所示.从图象可知,当且仅当x ∈(0,2)时,y<0.所以原不等式的解集是{x|0<x<2}.(2)当x ∈[-2a ,12）时, f(x)=1+a.不等式f(x)≤g(x)化为1+a ≤x+3.所以x ≥a-2对x ∈[-2a ,12）都成立. 故-2a ≥a-2, 即a ≤43. 从而a 的取值范围是（-1,43]. 5.(2012年辽宁卷,理24)已知f(x)=|ax+1|(a ∈R),不等式f(x)≤3的解集为{x|-2≤x ≤1}.(1)求a 的值;(2)若|f(x)-2f 2x ⎛⎫ ⎪⎝⎭|≤k 恒成立,求k 的取值范围. 解:(1)由|ax+1|≤3得-4≤ax ≤2.又f(x)≤3的解集为{x|-2≤x ≤1},所以当a ≤0时不合题意,当a>0时,-4a ≤x ≤2a, 所以a=2. (2)记h(x)=f(x)-2f 2x ⎛⎫ ⎪⎝⎭, 则h(x)=1,1143,1,211,.2x x x x ⎧⎪-⎪⎪----⎨⎪⎪--⎪⎩≤＜＜≥ 所以|h(x)|≤1,因此k ≥1.6.(2012年新课标全国卷,理24)已知函数f(x)=|x+a|+|x-2|.(1)当a=-3时,求不等式f(x)≥3的解集;(2)若f(x)≤|x-4|的解集包含[1,2],求a 的取值范围.解:(1)当a=-3时,f(x)=25,2,1,23,25, 3.x x x x x x -+⎧⎪⎨⎪-⎩≤＜＜≥当x ≤2时,由f(x)≥3得-2x+5≥3,解得x ≤1;当2<x<3时,f(x)≥3无解;当x ≥3时,由f(x)≥3得2x-5≥3,解得x ≥4.所以f(x)≥3的解集为{x|x ≤1或x ≥4}.(2)f(x)≤|x-4|⇔|x-4|-|x-2|≥|x+a|.当x ∈[1,2]时,|x-4|-|x-2|≥|x+a|⇔4-x-(2-x)≥|x+a|⇔-2-a ≤x ≤2-a.由条件得-2-a ≤1且2-a ≥2,即-3≤a ≤0.故满足条件的a 的取值范围为[-3,0].7.(2011年新课标全国卷,理24)设函数f(x)=|x-a|+3x,其中a>0.(1)当a=1时,求不等式f(x)≥3x+2的解集;(2)若不等式f(x)≤0的解集为{x|x ≤-1},求a 的值.解:(1)当a=1时,f(x)≥3x+2可化为|x-1|≥2.由此可得x ≥3或x ≤-1.故当a=1时,不等式f(x)≥3x+2的解集为{x|x ≥3或x ≤-1}.(2)由f(x)≤0得|x-a|+3x ≤0,此不等式可化为不等式组,30x a x a x ⎧⎨-+⎩≥≤或,30,x a a x x ⎧⎨-+⎩＜≤即,4x a a x ⎧⎪⎨⎪⎩≥≤或,,2x a a x ⎧⎪⎨-⎪⎩＜≤因为a>0,所以不等式组的解集为{x|x ≤-2a }, 由题设可得-2a =-1,故a=2. 考点二 不等式的证明1.(2013年新课标全国卷Ⅱ,理24)(选修45:不等式选讲)设a,b,c 均为正数,且a+b+c=1.证明:(1)ab+bc+ac ≤13; (2)2a b + 2b c +2c a≥1. 证明:(1)由a 2+b 2≥2ab,b 2+c 2≥2bc,c 2+a 2≥2ca, 得a 2+b 2+c 2≥ab+bc+ca. 由题设得(a+b+c)2=1, 即a 2+b 2+c 2+2ab+2bc+2ca=1. 所以3(ab+bc+ca)≤1,即ab+bc+ca ≤13. (2)因为2a b +b ≥2a,2b c +c ≥2b, 2c a+a ≥2c, 故2a b +2b c +2c a+(a+b+c)≥2(a+b+c), 即2a b +2b c +2c a≥a+b+c. 所以2a b +2b c +2c a≥1. 2.(2012年江苏卷,21D)已知实数x,y 满足|x+y|<13,|2x-y|<16,求证|y|<518. 证明:因为x,y 为实数,所以3|y|=|3y|=|2(x+y)-(2x-y)|≤2|x+y|+|2x-y|,由题设知|x+y|<13,|2x-y|<16,从而3|y|<23+16=56,所以|y|<5 18.3.(2011年安徽卷,理19)(1)设x≥1,y≥1,证明x+y+1xy≤1x+1y+xy;(2)设1<a≤b≤c,证明log a b+log b c+log c a≤log b a+log c b+log a c.证明:(1)由于x≥1,y≥1,所以x+y+1xy≤1x+1y+xy⇔xy(x+y)+1≤y+x+(xy)2.将上式中的右式减左式,得[y+x+(xy)2]-[xy(x+y)+1]=[(xy)2-1]-[xy(x+y)-(x+y)]=(xy+1)(xy-1)-(x+y)(xy-1)=(xy-1)(xy-x-y+1)=( xy-1)(x-1)(y-1).由于x≥1,y≥1,所以(xy-1)(x-1)(y-1)≥0.从而所要证明的不等式成立.(2)设log a b=x,log b c=y.由对数的换底公式得log c a=1xy,log b a=1x,log c b=1y,log a c=xy,于是所要证明的不等式为x+y+1xy≤1x+1y+xy.又由于1<a≤b≤c,所以x=log a b≥1,y=log b c≥1.故由(1)知所要证明的不等式成立.模拟试题考点一含绝对值不等式的解法1.(2013山东省实验中学测试)不等式3≤|5-2x|<9的解集是( )(A)(-∞,-2)∪(7,+∞)(B)[1,4](C)[-2,1]∪[4,7](D) (-2,1]∪[4,7)解析:由3≤|5-2x|<9得3≤2x-5<9,或-9<2x-5≤-3,即4≤x<7或-2<x≤1,所以不等式的解集为(-2,1]∪[4,7),故选D.答案:D2.(2013山东省实验中学测试)已知函数f(x)=|2x-a|+a.若不等式f(x)≤6的解集为{x|-2≤x≤3},则实数a的值为.解析:因为不等式f(x)≤6的解集为{x|-2≤x ≤3},即-2,3是方程f(x)=6的两个根,即|6-a|+a=6,|a+4|+a=6,所以|6-a|=6-a,|a+4|=6-a,即|6-a|=|a+4|,解得a=1.答案:13.(2011福州模拟)设函数f(x)=|x-1|+|x-a|.(1)若a=-1,解不等式f(x)≥3;(2)如果关于x 的不等式f(x)≥2恒成立,求a 的取值范围.解:(1)当a=-1时,f(x)=|x-1|+|x+1|.由f(x)≥3,得|x-1|+|x+1|≥3.①当x ≤-1时,不等式化为1-x-1-x ≥3,即x ≤-32. 所以,原不等式的解集为{x|x ≤-32}. ②当-1<x<1时,不等式化为1-x+1+x ≥3,即2≥3.所以,原不等式无解.③当x ≥1时,不等式化为-1+x+1+x ≥3,即x ≥32. 所以,原不等式的解集为{x|x ≥32}. 综上,原不等式的解集为(-∞,-32]∪[32,+∞). (2)因为关于x 的不等式f(x)≥2恒成立,所以,f(x)min ≥2.因为|x-1|+|x-a|表示数轴上的点到x=1与x=a 两点的距离之和,所以,f(x)min =|a-1|.∴|a-1|≥2,解得a ≤-1或a ≥3,所以,a 的取值范围为(-∞,-1]∪[3,+∞).考点二 不等式的证明1.(2011湖南十二校联考)若a,b,c 均为正数,且a 2+ab+ac+bc=4,则2a+b+c 的最小值为 .解析:a 2+ab+ac+bc=(a+b)(a+c)=4,由a,b,c 均为正数,可得2a+b+c=a+b+a+c ≥=4,当且仅当b=c 时取等号.答案:42.(2011福州模拟)已知a,b,c 均为正实数,且a+b+c=1..解2≤7+2(4a+1)+2(4b+1)+2(4c+1)=7+8(a+b+c)+6=21.当且仅当a=b=c=13时等号成立.综合检测1.(2012宝鸡质检)若不等式|2a-1|≤|x+1x|对一切非零实数x恒成立,则实数a的取值范围是.解析:∵x与1x同号,∴|x+1x|=|x|+|1x|≥2,当且仅当|x|=|1x|时取等号,若原不等式对任意非零实数x恒成立,则|2a-1|≤2,∴-2≤2a-1≤2,解得-12≤a≤32.答案:[-12,32]2.(2011泉州模拟)已知关于x的不等式|x+1|+|x-2|≤11a bb a⎛⎫⎛⎫++⎪⎪⎝⎭⎝⎭对任意正实数a、b恒成立,求实数x的取值范围.解:∵a>0,b>0,∴11a bb a⎛⎫⎛⎫++⎪⎪⎝⎭⎝⎭=2+ab+1ab≥4,当且仅当ab=1时取等号,∴11a bb a⎛⎫⎛⎫++⎪⎪⎝⎭⎝⎭的最小值为4,∴|x+1|+|x-2|≤4.当x≤-1时,-x-1+2-x≤4,x≥-3 2 ,∴-32≤x≤-1.当-1<x<2时,x+1+2-x≤4,3≤4,∴-1<x<2.当x≥2时,x+1+x-2≤4,x≤5 2 ,∴2≤x≤5 2 ,综上,x的取值范围是[-32,52].3.(2011福建模拟)已知a,b为正实数.(1)求证:2ab+2ba≥a+b;(2)利用(1)的结论求函数y=()21xx-+21xx-(0<x<1)的最小值.(1)证明:∵a>0,b>0,∴(a+b)(2ab+2ba)=a2+b2+3ab+3ba≥a2+b2+2ab=(a+b)2.∴2ab+2ba≥a+b,当且仅当a=b时等号成立.(2)解:∵0<x<1,∴1-x>0,由(1)的结论,函数y=()21xx-+21xx-≥(1-x)+x=1.当且仅当1-x=x即x=12时等号成立.∴函数y=()21xx-+21xx-(0<x<1)的最小值为1.。

历年高考数学真题精选（按考点分类）专题52 不等式选讲（学生版）1．（2019•新课标Ⅱ）已知f（x）＝|x﹣a|x+|x﹣2|（x﹣a）．（1）当a＝1时，求不等式f（x）＜0的解集；（2）当x∈（﹣∞，1）时，f（x）＜0，求a的取值范围．2．（2018•新课标Ⅰ）已知f（x）＝|x+1|﹣|ax﹣1|．（1）当a＝1时，求不等式f（x）＞1的解集；（2）若x∈（0，1）时不等式f（x）＞x成立，求a的取值范围．3．（2018•新课标Ⅱ）设函数f（x）＝5﹣|x+a|﹣|x﹣2|．（1）当a＝1时，求不等式f（x）≥0的解集；（2）若f（x）≤1，求a的取值范围．4．（2017•新课标Ⅰ）已知函数f（x）＝﹣x2+ax+4，g（x）＝|x+1|+|x﹣1|．（1）当a＝1时，求不等式f（x）≥g（x）的解集；（2）若不等式f（x）≥g（x）的解集包含[﹣1，1]，求a的取值范围．5．（2017•新课标Ⅲ）已知函数f（x）＝|x+1|﹣|x﹣2|．（1）求不等式f（x）≥1的解集；（2）若不等式f（x）≥x2﹣x+m的解集非空，求m的取值范围．6．（2016•新课标Ⅲ）已知函数f（x）＝|2x﹣a|+a．（1）当a＝2时，求不等式f（x）≤6的解集；（2）设函数g（x）＝|2x﹣1|，当x∈R时，f（x）+g（x）≥3，求a的取值范围．7．（2016•新课标Ⅱ）已知函数f（x）＝|x−12|+|x+12|，M为不等式f（x）＜2的解集．（Ⅰ）求M；（Ⅱ）证明：当a，b∈M时，|a+b|＜|1+ab|．8．（2015•新课标Ⅰ）已知函数f（x）＝|x+1|﹣2|x﹣a|，a＞0．（Ⅰ）当a＝1时，求不等式f（x）＞1的解集；（Ⅱ）若f（x）的图象与x轴围成的三角形面积大于6，求a的取值范围．9．（2014•新课标Ⅱ）设函数f（x）＝|x+1a|+|x﹣a|（a＞0）．（Ⅰ）证明：f （x ）≥2；（Ⅱ）若f （3）＜5，求a 的取值范围． 10．（2014•新课标Ⅰ）若a ＞0，b ＞0，且1a +1b=√ab ．（Ⅰ）求a 3+b 3的最小值；（Ⅱ）是否存在a ，b ，使得2a +3b ＝6？并说明理由．11．（2013•新课标Ⅰ）已知函数f （x ）＝|2x ﹣1|+|2x +a |，g （x ）＝x +3． （Ⅰ）当a ＝﹣2时，求不等式f （x ）＜g （x ）的解集；（Ⅱ）设a ＞﹣1，且当x ∈[−a 2，12]时，f （x ）≤g （x ），求a 的取值范围．12．（2011•辽宁）选修4﹣5：不等式选讲 已知函数f （x ）＝|x ﹣2|﹣|x ﹣5|． （1）证明：﹣3≤f （x ）≤3；（2）求不等式f （x ）≥x 2﹣8x +15的解集． 13．（2019•新课标Ⅲ）设x ，y ，z ∈R ，且x +y +z ＝1． （1）求（x ﹣1）2+（y +1）2+（z +1）2的最小值；（2）若（x ﹣2）2+（y ﹣1）2+（z ﹣a ）2≥13成立，证明：a ≤﹣3或a ≥﹣1． 14．（2019•新课标Ⅰ）已知a ，b ，c 为正数，且满足abc ＝1．证明： （1）1a +1b+1c≤a 2+b 2+c 2；（2）（a +b ）3+（b +c ）3+（c +a ）3≥24．15．（2017•新课标Ⅱ）已知a ＞0，b ＞0，a 3+b 3＝2．证明： （1）（a +b ）（a 5+b 5）≥4； （2）a +b ≤2．16．（2015•新课标Ⅱ）设a ，b ，c ，d 均为正数，且a +b ＝c +d ，证明： （1）若ab ＞cd ，则√a +√b ＞√c +√d ；（2）√a +√b ＞√c +√d 是|a ﹣b |＜|c ﹣d |的充要条件． 17．（2013•辽宁）（1）证明：当x ∈[0，1]时，√22x ≤sinx ≤x ； （2）若不等式ax +x 2+x 32+2(x +2)cosx ≤4对x ∈[0，1]恒成立，求实数a 的取值范围． 18．（2013•新课标Ⅱ）【选修4﹣﹣5；不等式选讲】 设a ，b ，c 均为正数，且a +b +c ＝1，证明：（Ⅰ）ab +bc +ca ≤13（Ⅱ）a 2b+b 2c+c 2a≥1．历年高考数学真题精选（按考点分类）专题52 不等式选讲（学生版）一．解答题（共18小题）1．（2019•新课标Ⅱ）已知f （x ）＝|x ﹣a |x +|x ﹣2|（x ﹣a ）． （1）当a ＝1时，求不等式f （x ）＜0的解集；（2）当x ∈（﹣∞，1）时，f （x ）＜0，求a 的取值范围． 解：（1）当a ＝1时，f （x ）＝|x ﹣1|x +|x ﹣2|（x ﹣1），∵f （x ）＜0，∴当x ＜1时，f （x ）＝﹣2（x ﹣1）2＜0，恒成立，∴x ＜1； 当x ≥1时，f （x ）＝（x ﹣1）（x +|x ﹣2|）≥0恒成立，∴x ∈∅； 综上，不等式的解集为（﹣∞，1）；（2）当a ≥1时，f （x ）＝2（a ﹣x ）（x ﹣1）＜0在x ∈（﹣∞，1）上恒成立； 当a ＜1时，x ∈（a ，1），f （x ）＝2（x ﹣a ）＞0，不满足题意， ∴a 的取值范围为：[1，+∞）2．（2018•新课标Ⅰ）已知f （x ）＝|x +1|﹣|ax ﹣1|． （1）当a ＝1时，求不等式f （x ）＞1的解集；（2）若x ∈（0，1）时不等式f （x ）＞x 成立，求a 的取值范围．解：（1）当a ＝1时，f （x ）＝|x +1|﹣|x ﹣1|={2，x ＞12x ，−1≤x ≤1−2，x ＜−1，由f （x ）＞1，∴{2x ＞1−1≤x ≤1或{2＞1x ＞1， 解得x ＞12，故不等式f （x ）＞1的解集为（12，+∞），（2）当x ∈（0，1）时不等式f （x ）＞x 成立， ∴|x +1|﹣|ax ﹣1|﹣x ＞0， 即x +1﹣|ax ﹣1|﹣x ＞0， 即|ax ﹣1|＜1，∴﹣1＜ax﹣1＜1，∴0＜ax＜2，∵x∈（0，1），∴a＞0，∴0＜x＜2 a，∴a＜2 x∵2x＞2，∴0＜a≤2，故a的取值范围为（0，2]．3．（2018•新课标Ⅱ）设函数f（x）＝5﹣|x+a|﹣|x﹣2|．（1）当a＝1时，求不等式f（x）≥0的解集；（2）若f（x）≤1，求a的取值范围．解：（1）当a＝1时，f（x）＝5﹣|x+1|﹣|x﹣2|={2x+4，x≤−1 2，−1＜x＜2−2x+6，x≥2．当x≤﹣1时，f（x）＝2x+4≥0，解得﹣2≤x≤﹣1，当﹣1＜x＜2时，f（x）＝2≥0恒成立，即﹣1＜x＜2，当x≥2时，f（x）＝﹣2x+6≥0，解得2≤x≤3，综上所述不等式f（x）≥0的解集为[﹣2，3]，（2）∵f（x）≤1，∴5﹣|x+a|﹣|x﹣2|≤1，∴|x+a|+|x﹣2|≥4，∴|x+a|+|x﹣2|＝|x+a|+|2﹣x|≥|x+a+2﹣x|＝|a+2|，∴|a+2|≥4，解得a≤﹣6或a≥2，故a的取值范围（﹣∞，﹣6]∪[2，+∞）．4．（2017•新课标Ⅰ）已知函数f（x）＝﹣x2+ax+4，g（x）＝|x+1|+|x﹣1|．（1）当a＝1时，求不等式f（x）≥g（x）的解集；（2）若不等式f（x）≥g（x）的解集包含[﹣1，1]，求a的取值范围．解：（1）当a ＝1时，f （x ）＝﹣x 2+x +4，是开口向下，对称轴为x =12的二次函数，g （x ）＝|x +1|+|x ﹣1|={2x ，x ＞12，−1≤x ≤1−2x ，x ＜−1，当x ∈（1，+∞）时，令﹣x 2+x +4＝2x ，解得x =√17−12，g （x ）在（1，+∞）上单调递增，f （x ）在（1，+∞）上单调递减，∴此时f （x ）≥g （x ）的解集为（1，√17−12]； 当x ∈[﹣1，1]时，g （x ）＝2，f （x ）≥f （﹣1）＝2．当x ∈（﹣∞，﹣1）时，g （x ）单调递减，f （x ）单调递增，且g （﹣1）＝f （﹣1）＝2． 综上所述，f （x ）≥g （x ）的解集为[﹣1，√17−12]； （2）依题意得：﹣x 2+ax +4≥2在[﹣1，1]恒成立，即x 2﹣ax ﹣2≤0在[﹣1，1]恒成立，则只需{12−a ⋅1−2≤0(−1)2−a(−1)−2≤0，解得﹣1≤a ≤1，故a 的取值范围是[﹣1，1]．5．（2017•新课标Ⅲ）已知函数f （x ）＝|x +1|﹣|x ﹣2|． （1）求不等式f （x ）≥1的解集；（2）若不等式f （x ）≥x 2﹣x +m 的解集非空，求m 的取值范围．解：（1）∵f （x ）＝|x +1|﹣|x ﹣2|={−3，x ＜−12x −1，−1≤x ≤23，x ＞2，f （x ）≥1，∴当﹣1≤x ≤2时，2x ﹣1≥1，解得1≤x ≤2； 当x ＞2时，3≥1恒成立，故x ＞2； 综上，不等式f （x ）≥1的解集为{x |x ≥1}．（2）原式等价于存在x ∈R 使得f （x ）﹣x 2+x ≥m 成立， 即m ≤[f （x ）﹣x 2+x ]max ，设g （x ）＝f （x ）﹣x 2+x ．由（1）知，g （x ）={−x 2+x −3，x ≤−1−x 2+3x −1，−1＜x ＜2−x 2+x +3，x ≥2，当x ≤﹣1时，g （x ）＝﹣x 2+x ﹣3，其开口向下，对称轴方程为x =12＞−1， ∴g （x ）≤g （﹣1）＝﹣1﹣1﹣3＝﹣5；当﹣1＜x ＜2时，g （x ）＝﹣x 2+3x ﹣1，其开口向下，对称轴方程为x =32∈（﹣1，2）， ∴g （x ）≤g （32）=−94+92−1=54；当x ≥2时，g （x ）＝﹣x 2+x +3，其开口向下，对称轴方程为x =12＜2， ∴g （x ）≤g （2）＝﹣4+2+3＝1； 综上，g （x ）max =54，∴m 的取值范围为（﹣∞，54]．6．（2016•新课标Ⅲ）已知函数f （x ）＝|2x ﹣a |+a ． （1）当a ＝2时，求不等式f （x ）≤6的解集；（2）设函数g （x ）＝|2x ﹣1|，当x ∈R 时，f （x ）+g （x ）≥3，求a 的取值范围． 解：（1）当a ＝2时，f （x ）＝|2x ﹣2|+2， ∵f （x ）≤6，∴|2x ﹣2|+2≤6， |2x ﹣2|≤4，|x ﹣1|≤2， ∴﹣2≤x ﹣1≤2， 解得﹣1≤x ≤3，∴不等式f （x ）≤6的解集为{x |﹣1≤x ≤3}． （2）∵g （x ）＝|2x ﹣1|，∴f （x ）+g （x ）＝|2x ﹣1|+|2x ﹣a |+a ≥3， 2|x −12|+2|x −a 2|+a ≥3， |x −12|+|x −a 2|≥3−a2， 当a ≥3时，成立，当a ＜3时，|x −12|+|x −a 2|≥12|a ﹣1|≥3−a2＞0， ∴（a ﹣1）2≥（3﹣a ）2， 解得2≤a ＜3，∴a 的取值范围是[2，+∞）．7．（2016•新课标Ⅱ）已知函数f （x ）＝|x −12|+|x +12|，M 为不等式f （x ）＜2的解集． （Ⅰ）求M ；（Ⅱ）证明：当a ，b ∈M 时，|a +b |＜|1+ab |．解：（I ）当x ＜−12时，不等式f （x ）＜2可化为：12−x ﹣x −12＜2，解得：x ＞﹣1， ∴﹣1＜x ＜−12，当−12≤x ≤12时，不等式f （x ）＜2可化为：12−x +x +12=1＜2，此时不等式恒成立， ∴−12≤x ≤12，当x ＞12时，不等式f （x ）＜2可化为：−12+x +x +12＜2， 解得：x ＜1， ∴12＜x ＜1，综上可得：M ＝（﹣1，1）； 证明：（Ⅱ）当a ，b ∈M 时， （a 2﹣1）（b 2﹣1）＞0， 即a 2b 2+1＞a 2+b 2，即a 2b 2+1+2ab ＞a 2+b 2+2ab ， 即（ab +1）2＞（a +b ）2， 即|a +b |＜|1+ab |．8．（2015•新课标Ⅰ）已知函数f （x ）＝|x +1|﹣2|x ﹣a |，a ＞0． （Ⅰ）当a ＝1时，求不等式f （x ）＞1的解集；（Ⅱ）若f （x ）的图象与x 轴围成的三角形面积大于6，求a 的取值范围． 解：（Ⅰ）当a ＝1时，不等式f （x ）＞1，即|x +1|﹣2|x ﹣1|＞1， 即{x ＜−1−x −1−2(1−x)＞1①，或{−1≤x ＜1x +1−2(1−x)＞1②，或{x ≥1x +1−2(x −1)＞1③． 解①求得x ∈∅，解②求得23＜x ＜1，解③求得1≤x ＜2．综上可得，原不等式的解集为（23，2）．（Ⅱ）函数f （x ）＝|x +1|﹣2|x ﹣a |={x −1−2a ，x ＜−13x +1−2a ，−1≤x ≤a −x +1+2a ，x ＞a，由此求得f （x ）的图象与x 轴的交点A （2a−13，0），B （2a +1，0），故f （x ）的图象与x 轴围成的三角形的第三个顶点C （a ，a +1）， 由△ABC 的面积大于6， 可得12[2a +1−2a−13]•（a +1）＞6，求得a ＞2． 故要求的a 的范围为（2，+∞）．9．（2014•新课标Ⅱ）设函数f （x ）＝|x +1a |+|x ﹣a |（a ＞0）． （Ⅰ）证明：f （x ）≥2；（Ⅱ）若f （3）＜5，求a 的取值范围．解：（Ⅰ）证明：∵a ＞0，f （x ）＝|x +1a |+|x ﹣a |≥|（x +1a ）﹣（x ﹣a ）|＝|a +1a |＝a +1a ≥2√a ⋅1a =2， 故不等式f （x ）≥2成立． （Ⅱ）∵f （3）＝|3+1a |+|3﹣a |＜5，∴当a ＞3时，不等式即a +1a＜5，即a 2﹣5a +1＜0，解得3＜a ＜5+√212． 当0＜a ≤3时，不等式即 6﹣a +1a ＜5，即 a 2﹣a ﹣1＞0，求得1+√52＜a ≤3． 综上可得，a 的取值范围（1+√52，5+√212）．10．（2014•新课标Ⅰ）若a ＞0，b ＞0，且1a+1b=√ab ．（Ⅰ）求a 3+b 3的最小值；（Ⅱ）是否存在a ，b ，使得2a +3b ＝6？并说明理由． 解：（Ⅰ）∵a ＞0，b ＞0，且1a+1b=√ab ，∴√ab =1a +1b ≥2√1ab ，∴ab ≥2， 当且仅当a ＝b =√2时取等号．∵a 3+b 3 ≥2√(ab)3≥2√23=4√2，当且仅当a ＝b =√2时取等号， ∴a 3+b 3的最小值为4√2．（Ⅱ）∵2a +3b ≥2√2a ⋅3b =2√6ab ，当且仅当2a ＝3b 时，取等号． 而由（1）可知，2√6ab ≥2√12=4√3＞6， 故不存在a ，b ，使得2a +3b ＝6成立．11．（2013•新课标Ⅰ）已知函数f （x ）＝|2x ﹣1|+|2x +a |，g （x ）＝x +3． （Ⅰ）当a ＝﹣2时，求不等式f （x ）＜g （x ）的解集；（Ⅱ）设a ＞﹣1，且当x ∈[−a 2，12]时，f （x ）≤g （x ），求a 的取值范围．解：（Ⅰ）当a ＝﹣2时，求不等式f （x ）＜g （x ）化为|2x ﹣1|+|2x ﹣2|﹣x ﹣3＜0． 设y ＝|2x ﹣1|+|2x ﹣2|﹣x ﹣3，则y ={−5x ，x ＜12−x −2，12≤x ≤13x −6，x ＞1，它的图象如图所示：结合图象可得，y ＜0的解集为（0，2），故原不等式的解集为（0，2）． （Ⅱ）设a ＞﹣1，且当x ∈[−a2，12]时，f （x ）＝1+a ，不等式化为1+a ≤x +3，故x ≥a ﹣2对x ∈[−a 2，12]都成立．故−a 2≥a ﹣2， 解得a ≤43，故a 的取值范围为（﹣1，43]．12．（2011•辽宁）选修4﹣5：不等式选讲已知函数f （x ）＝|x ﹣2|﹣|x ﹣5|．（1）证明：﹣3≤f （x ）≤3；（2）求不等式f （x ）≥x 2﹣8x +15的解集．解：（1）f （x ）＝|x ﹣2|﹣|x ﹣5|={−3，x ≤22x −7，2＜x ＜53，x ≥5．当2＜x ＜5时，﹣3＜2x ﹣7＜3．所以﹣3≤f （x ）≤3．（2）由（1）可知，当x ≤2时，f （x ）≥x 2﹣8x +15的解集为空集；当2＜x ＜5时，f （x ）≥x 2﹣8x +15的解集为{x |5−√3≤x ＜5}；当x ≥5时，f （x ）≥x 2﹣8x +15的解集为{x |5≤x ≤6}．综上，不等式f （x ）≥x 2﹣8x +15的解集为{x |5−√3≤x ≤6}．13．（2019•新课标Ⅲ）设x ，y ，z ∈R ，且x +y +z ＝1．（1）求（x ﹣1）2+（y +1）2+（z +1）2的最小值；（2）若（x ﹣2）2+（y ﹣1）2+（z ﹣a ）2≥13成立，证明：a ≤﹣3或a ≥﹣1．解：（1）x ，y ，z ∈R ，且x +y +z ＝1，由柯西不等式可得（12+12+12）[（x ﹣1）2+（y +1）2+（z +1）2]≥（x ﹣1+y +1+z +1）2＝4，可得（x ﹣1）2+（y +1）2+（z +1）2≥43，即有（x ﹣1）2+（y +1）2+（z +1）2的最小值为43； （2）证明：由x +y +z ＝1，柯西不等式可得（12+12+12）[（x ﹣2）2+（y ﹣1）2+（z ﹣a ）2]≥（x ﹣2+y ﹣1+z ﹣a ）2＝（a +2）2，可得（x ﹣2）2+（y ﹣1）2+（z ﹣a ）2≥(a+2)23， 即有（x ﹣2）2+（y ﹣1）2+（z ﹣a ）2的最小值为(a+2)23， 由题意可得(a+2)23≥13， 解得a ≥﹣1或a ≤﹣3．14．（2019•新课标Ⅰ）已知a ，b ，c 为正数，且满足abc ＝1．证明：（1）1a +1b +1c ≤a 2+b 2+c 2；（2）（a +b ）3+（b +c ）3+（c +a ）3≥24．证明：（1）分析法：已知a ，b ，c 为正数，且满足abc ＝1．要证（1）1a +1b +1c ≤a 2+b 2+c 2；因为abc ＝1．就要证：abc a +abc b +abc c ≤a 2+b 2+c 2；即证：bc +ac +ab ≤a 2+b 2+c 2；即：2bc +2ac +2ab ≤2a 2+2b 2+2c 2；2a 2+2b 2+2c 2﹣2bc ﹣2ac ﹣2ab ≥0（a ﹣b ）2+（a ﹣c ）2+（b ﹣c ）2≥0；∵a ，b ，c 为正数，且满足abc ＝1．∴（a ﹣b ）2≥0；（a ﹣c ）2≥0；（b ﹣c ）2≥0恒成立；当且仅当：a ＝b ＝c ＝1时取等号． 即（a ﹣b ）2+（a ﹣c ）2+（b ﹣c ）2≥0得证．故1a +1b +1c ≤a 2+b 2+c 2得证．（2）证（a +b ）3+（b +c ）3+（c +a ）3≥24成立；即：已知a ，b ，c 为正数，且满足abc ＝1．（a +b ）为正数；（b +c ）为正数；（c +a ）为正数；（a +b ）3+（b +c ）3+（c +a ）3≥3（a +b ）•（b +c ）•（c +a ）；当且仅当（a +b ）＝（b +c ）＝（c +a ）时取等号；即：a ＝b ＝c ＝1时取等号； ∵a ，b ，c 为正数，且满足abc ＝1．（a +b ）≥2√ab ；（b +c ）≥2√bc ；（c +a ）≥2√ac ；当且仅当a ＝b ，b ＝c ；c ＝a 时取等号；即：a ＝b ＝c ＝1时取等号；∴（a +b ）3+（b +c ）3+（c +a ）3≥3（a +b ）•（b +c ）•（c +a ）≥3×8√ab •√bc •√ac =24abc ＝24；当且仅当a ＝b ＝c ＝1时取等号；故（a +b ）3+（b +c ）3+（c +a ）3≥24．得证．故得证．15．（2017•新课标Ⅱ）已知a ＞0，b ＞0，a 3+b 3＝2．证明：（1）（a +b ）（a 5+b 5）≥4；（2）a +b ≤2．证明：（1）由柯西不等式得：（a +b ）（a 5+b 5）≥（√a ⋅a 5+√b ⋅b 5）2＝（a 3+b 3）2≥4， 当且仅当√ab 5=√ba 5，即a ＝b ＝1时取等号，（2）∵a 3+b 3＝2，∴（a +b ）（a 2﹣ab +b 2）＝2，∴（a +b ）[（a +b ）2﹣3ab ]＝2，∴（a +b ）3﹣3ab （a +b ）＝2，∴(a+b)3−23(a+b)=ab ，由均值不等式可得：(a+b)3−23(a+b)=ab ≤（a+b 2）2， ∴（a +b ）3﹣2≤3(a+b)34， ∴14（a +b ）3≤2， ∴a +b ≤2，当且仅当a ＝b ＝1时等号成立．16．（2015•新课标Ⅱ）设a ，b ，c ，d 均为正数，且a +b ＝c +d ，证明：（1）若ab ＞cd ，则√a +√b ＞√c +√d ；（2）√a +√b ＞√c +√d 是|a ﹣b |＜|c ﹣d |的充要条件．证明：（1）由于（√a +√b ）2＝a +b +2√ab ，（√c +√d ）2＝c +d +2√cd ，由a ，b ，c ，d 均为正数，且a +b ＝c +d ，ab ＞cd ，则√ab ＞√cd ，即有（√a +√b ）2＞（√c +√d ）2，则√a +√b ＞√c +√d ；（2）①若√a +√b ＞√c +√d ，则（√a +√b ）2＞（√c +√d ）2，即为a +b +2√ab ＞c +d +2√cd ，由a +b ＝c +d ，则ab ＞cd ，于是（a ﹣b ）2＝（a +b ）2﹣4ab ，（c ﹣d ）2＝（c +d ）2﹣4cd ，即有（a ﹣b ）2＜（c ﹣d ）2，即为|a ﹣b |＜|c ﹣d |；②若|a ﹣b |＜|c ﹣d |，则（a ﹣b ）2＜（c ﹣d ）2，即有（a +b ）2﹣4ab ＜（c +d ）2﹣4cd ，由a +b ＝c +d ，则ab ＞cd ，则有（√a +√b ）2＞（√c +√d ）2．综上可得，√a +√b ＞√c +√d 是|a ﹣b |＜|c ﹣d |的充要条件．17．（2013•辽宁）（1）证明：当x ∈[0，1]时，√22x ≤sinx ≤x ； （2）若不等式ax +x 2+x 32+2(x +2)cosx ≤4对x ∈[0，1]恒成立，求实数a 的取值范围． （1）证明：记F （x ）＝sin x −√22x ，则F ′（x ）＝cos x −√22． 当x ∈（0，π4）时，F ′（x ）＞0，F （x ）在[0，π4]上是增函数；当x ∈（π4，1）时，F ′（x ）＜0，F （x ）在[π4，1]上是减函数； 又F （0）＝0，F （1）＞0，所以当x ∈[0，1]时，F （x ）≥0，即sin x ≥√22x ，记H （x ）＝sin x ﹣x ，则当x ∈（0，1）时，H ′（x ）＝cos x ﹣1＜0，所以H （x ）在[0，1]上是减函数；则H （x ）≤H （0）＝0，即sin x ≤x ．综上，√22x ≤sin x ≤x ． （2）∵当x ∈[0，1]时，ax +x 2+x 32+2（x +2）cos x ﹣4＝（a +2）x +x 2+x 32−4（x +2）sin 2x 2≤（a +2）x +x 2+x 32−4（x +2）(√24x)2＝（a +2）x ，∴当a ≤﹣2时，不等式ax +x 2+x 32+2（x +2）cos x ≤4对x ∈[0，1]恒成立，下面证明，当a ＞﹣2时，不等式ax +x 2+x 32+2（x +2）cos x ≤4对x ∈[0，1]不恒成立． ∵当x ∈[0，1]时，ax +x 2+x 32+2（x +2）cos x ﹣4＝（a +2）x +x 2+x 32−4（x +2）sin 2x 2≥（a +2）x +x 2+x 32−4（x +2）(x 2)2＝（a +2）x ﹣x 2−x 32≥（a +2）x −32x 2=−32x [x −23（a +2）]．所以存在x 0∈（0，1）（例如x 0取a+23和12中的较小值）满足ax 0+x 02+x032+2（x 0+2）cos x 0﹣4＞0，即当a ＞﹣2时，不等式ax +x 2+x 32+2（x +2）cos x ≤4对x ∈[0，1]不恒成立．综上，实数a 的取值范围是（﹣∞，﹣2]．18．（2013•新课标Ⅱ）【选修4﹣﹣5；不等式选讲】设a ，b ，c 均为正数，且a +b +c ＝1，证明：（Ⅰ）ab +bc +ca ≤13（Ⅱ）a 2b +b2c +c 2a ≥1．证明：（Ⅰ）由a 2+b 2≥2ab ，b 2+c 2≥2bc ，c 2+a 2≥2ca 得a 2+b 2+c 2≥ab +bc +ca ， 由题设得（a +b +c ）2＝1，即a 2+b 2+c 2+2ab +2bc +2ca ＝1，所以3（ab +bc +ca ）≤1，即ab +bc +ca ≤13．（Ⅱ）因为a2b +b ≥2a ，b2c +c ≥2b ，c 2a +a ≥2c ，故a 2b +b 2c +c2a +（a +b +c ）≥2（a +b +c ），即a 2b +b2c +c 2a ≥a +b +c ．所以a 2b +b 2c +c 2a ≥1．。