信号与系统课件--差分方程齐次解单根例

x (t ) (t mT )
a

0 T
(t mT )
• • •
t
mT
ˆ xa (t )
m
x (mT ) (t mT )
a

0 T
T (t )
1
-2 -1 0 1 2
t
P ( j)
T
s

s
s
下面研究理想采样前后信号频谱的变化 我们知道，两信号在时域相乘的傅立叶变换等于两信号分别的傅立 叶变换的卷积 ˆ 按照 xa (t ) xa (mT ) (t mT ) 推导如下：
m
xa (mT )h(t mT )

t
0 T 2T 3T
sin[ (t mT )] T xa ( mT ) C m m (t ) m m (t mT ) T
X a ( j)
c
0
•
2
•
s
s
•
2 s
•
3s

ˆ X a ( j )
0
s 2
•
•
s
•
2 s
•
3s

3、（时域）采样定理
采样定理：当抽样频率大于信号最高频率的两倍时，
抽样后信号的频谱是原信号频谱的周期延拓而无混叠现 象，表明抽样没有丢失信息，有可能再恢复出原信号
频谱不混迭的条件 c 式中
h(0) ah( 1) 1 0 1 1
h(1) ah(0) 0 a 0 a
h(n) ah(n 1) 0 a n 0 a n
a n h( n) a u ( n) 0

(2) (b)计算零状态响应:
yzs [k ]
n
x[n]h[k
n]
u[k
]
3(
1 2
)
k
2( 1 ) k 3
u[k
]
n
u[n]
3(
1 2
)kn
2( 1 ) k n 3
u[k
-
n]
k n0
3(
1 2
)k
n
2( 1 ) k n 3
k 3(1 )kn k 2(1)kn
n0 2
CLTI系统数学模型——线性常系数微分方程，冲
激响应h(t);系统函数H(s);频率响应特性H( jw)
H (s) Yzs (s) X (s)
LT
h(t) H(s)
H ( j) H (s) |s j (系统稳定)
FT
h(t) H(j )
26
DLTI系统数学模型——线性常系数差分方程；冲
激响应h(n);系统函数H(z);频率响应特性H(ejw).
则
yzi[k ]
C1
(
1 2
)k
C2
(
1 )k 3
，k
0
代入初始条件,有:
y[1] 2C1 3C2 0
y[2] 4C1 9C2 1 C1 1/ 2, C2 1/ 3
则
yzi[k ]
1 2
(1)k 2
1 3
( 1 ) k ，k 3
0
= ( 1 )k1 (1)k1，k 0
2
3
17
n0 3
[ 3 3(1)k (1)k ]u[k] 23
完全响应: y[k] yzi[k] yzs[k]
[ 1 7 (1)k 4 (1)k ]u[k]

电信学院
1
前向差分方程
查公式
考虑二阶系统：
y(k 2) a1y(k 1) a0 y(k) b2 f (k 2) b1 f (k 1) b0 f (k)
初始值：yzi (0), yzi (1)
两边取Z变换有：
(z2 a1z a0 )Y (z) yzi (0)z2 yzi (1)z a1yzi (0)z (b2z2 b1z b0 )F(z)
1
(z
1)( z
2)
z
1
3
z
1
z
1
3
z
2
全响应
yzs (k )
[2 3
(1)k
1 3
(2)k
] (k)
y(k)
yzi
(k)
yzs (k )
[
2 3
6(1)k
2 3
(2)k
]
(k)
电信学院 返回
8
例 5.12 解 法 二
y(k 2) 3y(k 1) 2y(k) f (k 1) 3 f (k) yzi(1)=1, yzi(2)=3
F(z)
Y (z) Yzi (z) Yzs (z) 零输入响应
零状态响应
电信学院
3
系统函数
定义
H
(z)
零状态响应的z变换 激励信号的z变换
Yzs (z) F(z)
二阶系统零状态响应
Yzs (z)
b2z2 b1z b0 z2 a1z a0
F(z)
H (z)F (z)
对n阶LTI系统的系统函数
(b2z2 b1z b0 )F(z) b2 f (0)z2 b2 f (1)z b1 f (0)z
令：M (z) [ y(0) b2 f (0)]z2 [ y(1) a1y(0) b2 f (1) b1 f (0)]z

《高数3差分方程》PPT课件
# 高数3差分方程 PPT课件 ## 简介 - 差分方程的定义 - 差分方程的应用领域
什么是差分方程？
定义
差分方程是描述离散变量之间关系的数学方程。
应用领域
差分方程广泛应用于物理学、经济学、生物学和工程学等各个领域。
离散与连续
差分方程与微分方程的联系与区别。
常见的差分方程类型
参考资料
1 差分方程相关教材
《差分方程导论》、《差 分方程与重积分》等。
2 差分方程的相关论文
搜寻关于差分方程研究的 最新论文。
3 差分方程的相关网站
浏览在线差分方程教程和 实例应用。
通过求解两个线性齐 次差分方程的通解并 取其乘积得到非齐次 差分方程的通解。
齐次线性差分 方程通解的求 法
根据初始条件求解齐 次线性差分方程的通 解。
非齐次线性差 分方程通解的 求法
根据初始条件和非齐 次项求解非齐次线性 差分方程的通解。
差分方程在实际应用中的重要性
经济学中的应用
差分方程可用于描述经济模型中的离散变化。
生物学中的应用
差分方程可用于模拟生物体内离散变量的变化 规律。
物理学中的应用
差分方程可用于研究离散物理系统的演化。
工程学中的应用
差分方程可用于分析工程系统中的离散变化与 其他参数之间的关系。
总结
差分方程是研究离散变量之间关系的重要工具，广泛应用于各个学科中。了 解差分方程的基础知识和求解方法对深入理解实际问题具有重要意义。
1
一阶线性常微分方程
描述离散变量一阶导数与其他变量之间的关系。
2
二阶线性常微分方程
描述离散变量二阶导数与其他变量之间的关系。

里采用Z变换法来求解差分方程，这在实际使用上是最
Hale Waihona Puke 简单有效的方法。.精品课件.
3
例题：
若系统用差分方程y(n)=ay(n-1)+x(n)描述，输入序列 x(n)=δ(n)，求初始条件分别为：（1）h(n)=0，n<0；
（2）h(n)=0，n>0时的单位脉冲响应h(n)。 解：（1）令x(n)=δ(n)， y(n)= h(n)=0， n<0
x(n)
y(n)
Z-1
a
该式说明，系统在某时刻n的输出值y(n)不仅与该 时刻的输入x(n) 有关，还与该时刻以前的输出值 y(n-1)，y(n-2)等有关。
.精品课件.
7
§1.4 连续时间信号的抽样
模拟 前置预 滤波器
xa(t)
PrF
A/D 变换器
ADC
数字信号 处理器
DSP
D/A 变换器
DAC
§1.3 离散时间系统的时域描述––––差分方程
连续时间系统——用微分方程描述系统输出输入之间 的关系。
离散时间系统——用差分方程描述或研究输出输入之 间的关系。
一、常系数线性差分方程的一般表达式
N
M
ak y(n k) br x(n r) , a0 1
k0
r0
或
M
N
y(n) br x(n r) ak y(n k)
……
由y(n) ay(n 1) x(n)，得 y(1) ay(0) x(1) 0 y(2) ay(1) x(2) 0
y(n)=ay(n-1)=-an
y(n) 0，n 1
因此，h(n)=y(n)=-anu(-n-1)，是非因果系统。

频域分析法通过研究系统对不同频率信号的响应 特性，可以深入了解系统的频率特性。
简化计算
在频域中，常采用傅里叶变换等数学工具将信号 分解为不同频率的分量，从而简化计算过程。
3
局限性
频域分析法主要适用于线性时不变系统，对于非 线性或时变系统，频域分析法的应用受到限制。
变换域分析法
变换工具
变换域分析法通过采用拉普拉斯变换、Z变换等数学工具，将时间 域或频率域的信号转换到复平面上的另一域进行分析。
齐次性
若激励信号$x(t)$使系统产生响应 $y(t)$，则激励信号$kx(t)$使系统产 生的响应为$ky(t)$。
时不变特性
延迟性
若激励信号$x(t)$使系统产生响应 $y(t)$，则激励信号$x(t-t_0)$使系统 产生的响应为$y(t-t_0)$。
起始状态无关性
系统的输出只与输入信号有关，与系 统的起始状态无关。
MATLAB数据类型与运 算
深入介绍MATLAB中的数值类型、字符类型 、逻辑类型等数据类型，以及相应的运算规 则。
利用MATLAB进行信号生成与处理
信号生成
01
讲解如何使用MATLAB生成常见的基本信号，如正弦波、余弦
波、方波、锯齿波等。
信号处理
02
详细介绍MATLAB中信号处理的基本方法，包括信号的加减、
系统稳定性
在变换域中，可以方便地分析系统的稳定性，如通过判断系统函数 的极点位置来确定系统的稳定性。
系统性能评估
通过变换域分析法，可以对系统的性能指标如幅频特性、相频特性 等进行全面评估。
03 线性时不变系统特性
线性特性
叠加性
若对两个激励信号$x_1(t)$和$x_2(t)$， 系统分别有响应$y_1(t)$和$y_2(t)$，则 对叠加的激励$ax_1(t)+bx_2(t)$，系统 的响应为$ay_1(t)+by_2(t)$。

41
4. 指数信号 指数信号的一般数学表达式为
f(t)=Aest
根据式中s的不同取值，可以分下列两种情况讨论： (1) s=σ时，此时为实指数信号，即
(1-23)
f(t)=Aeσt
(1-24)
当σ>0时，信号呈指数规律增长；当σ<0时，信号随指数规律
衰减；当σ=0时，指数信号变成恒定不变的直流信号，如图1-
16所示。
42
图1-16 实指数信号
43
(2) s=σ+jω，此时为复指数信号。利用欧拉公式，可以进 一步表示为
(1-25) 可见，复指数信号的实部和虚部都是振幅按指数规律变化的 正弦振荡，当σ>0(σ<0)时，其实部和虚部的振幅按指数规律增 长(衰减)；当σ=0时，复指数信号变为虚指数信号
(1-26) 此时信号的实部和虚部都是等幅振荡的正弦波。复指数信号 虚部的波形如图1-17所示。
f(t)δ(t)=f(0)δ(t)
若f(t)在t=t0时连续，则有
f(t)δ(t－t0)=f(t0)δ(t－t0)
(1-16) (1-17)
36
对上面两式取积分，可得到下面两个重要的积分结果: (1-18) (1-19)
式(1-19)说明，δ(t)函数可以把信号f(t)在某时刻的值采样(筛选) 出来，这就是δ(t)的筛选性。
11
图1-4 非周期能量信号
12
图1-5 非周期功率信号
13
图1-6 非功率非能量信号
14
1.2.2 几种常用的基本信号 1. 单位斜变信号 斜变信号是指从某一时刻开始随时间成正比例增加的信
号。斜变信号也称斜坡信号。若斜变信号增长的变化率为1， 斜变的起始点发生在t=0时刻，就称其为单位斜变信号(如图 1-7所示)，其数学表达式为

T T

T
f (t ) dt
f (t ) dt
2
2
（1.1-1）
1 P lim T 2T

T
T
（ 1.1-2 ）
上两式中，被积函数都是f ( t )的绝对值平方，所以信号能量 E 和信号功率P 都是非负实数。 若信号f ( t )的能量0 < E < , 此时P = 0，则称此信号 为能量有限信号，简称能量信号（energy signal）。 若信号f ( t )的功率0 < P < , 此时E = ，则称此信 号为功率有限信号，简称功率信号（power signal）。 信号f ( t )可以是一个既非功率信号，又非能量信号， 如单位斜坡信号就是一个例子。但一个信号不可能同时既是 功率信号，又是能量信号。
1.3 系统的数学模型及其分类
1.3.1 系统的概念 什么是系统（ system ）？广义地说，系统是由若干相互作用 和相互依赖的事物组合而成的具有特定功能的整体。例如， 通信系统、自动控制系统、计算机网络系统、电力系统、水 利灌溉系统等。通常将施加于系统的作用称为系统的输入激 励；而将要求系统完成的功能称为系统的输出响应。 1.3.2 系统的数学模型 分析一个实际系统，首先要对实际系统建立数学模型，在数 学模型的基础上，再根据系统的初始状态和输入激励，运用 数学方法求其解答，最后又回到实际系统，对结果作出物理 解释，并赋予物理意义。所谓系统的模型是指系统物理特性 的抽象，以数学表达式或具有理想特性的符号图形来表征系 统特性。
2．连续信号和离散信号 按照函数时间取值的连续性划分，确定信号可分为连续时 间信号和离散时间信号，简称连续信号和离散信号。 连续信号（ continuous signal）是指在所讨论的时间内，对 任意时刻值除若干个不连续点外都有定义的信号，通常用f ( t ) 表示。 离散信号（discrete signal）是指只在某些不连续规定的时刻 有定义，而在其它时刻没有定义的信号。通常用 f(tk) 或 f(kT) [简写 f(k )] 表示，如图1.1-2所示。图中信号 f (tk) 只在t k = －2, －1, 0, 1, 2, 3,…等离散时刻才给出函数值。

Ba k
(不含等于a的特征根)
( B1k B0 )a k
(含一个等于a的特征根)
( Br k r Br 1k r 1 B0 )a k
(含有r个等于a的特征根)
例：已知某系统激励为零，初始值y(0)=0， y(1)=2，描述系统的差分方程 y(k ) 3 y(k 1) 2 y(k 为 2k U (k ) 求系统的响应 y(k)。 2) 解： 2
1 1 (2) 求零状态响应： f (k ) y0 (k ) yt (k ) y yt (k ) ( ) k 15 2 1 1 k k k y f (k ) A1 (1) A2 (2) ( ) 15 2
递推得：y(0)=1， y(1)=-2.5，并代入上式，有
2 8 1 1 y f (k ) (1) k (2) k ( ) k 3 5 15 2
解：
递推求初值：
代入通解求待定系数：
h(k ) 5h(k 1) 6h(k 2) (k ) h(0) 5h(1) 6h(2) f (0) 1 h(1) 5h(0) 6h(1) (1) 5
h(0) [ A1 A2 ] 1 h(1) [ A1 (2) A2 (3)] 5
i 1
r i
E1
k
i r 1
Ai E i
n
k
例1：已知某系统激励为零，初始值y(0) =1 ， y(1)=4，描述系统的差 y(k ) 5 y(k 1) 6 y(k 2) 0 求系统的响应 y(k)。 分方程为 解： 1 5E 1 6 E 2 0 或 E 2 5E 6 0
y(k-1)E-1 y(k)

2 an T1

T1 2 T 1 2
f ( t )dt
余弦分量 系数 正弦分量 系数

T1 2 T 1 2
f ( t ) cos(n1t )dt
2 bn T1

T1 2 T 1 2
f ( t ) sin( n1t )dt
注意！
傅立叶级数与傅立叶系数的联系与区别
指数形式傅立叶级数的傅里叶系数
尺度变换、初值、终值
卷积特性 拉氏逆变换

部分分式展开法（求系数）

系统函数H(s)
定义（两种定义方式）
求解（依据两种定义方式）
第四章 拉普拉斯变换、 连续时间系统的s域分析
收敛域：实际上就是拉氏变换存在的条件；
σ t
lim f (t ) e
t
0
σ σ0
三．一些常用函数的拉氏变换
t n st n n1 st e t e dt s 0 s 0
n n1 st t e dt s 0 n n 1 n 所以 L t L t s n1



Lt t e d t
st 0
1 1 st 1 e s2 s s 0 n2 2 2 1 2 2 L t Lt 2 3 s s s s n3 3 2 3 2 6 3 Lt Lt 3 4 s s s s
1 sin( t ) (e jt e jt ) 2j 1 cos(t ) (e jt e jt ) 2
推出 公式
第一章 绪论
关于冲激信号
(at )
1 (t ) a
尺度变换特性
(t ) f (t ) f (0) (t )

a
n
y ( n) y (n 1)
N k 0
y(n) ca
n
一般情况下：令 y c 代入 a k y ( n k ) 0
ak c nk 0 消去c，除以 n N
可得 a0 有N个根
k 0
N
N
a N 1 aN 1 aN 0 特征方程 特征根 1 , 2 ,, N
§7.4 线性常系数差分方程的求解
①例子 例7：第一类型（方程右端无x (n ) 项，即齐次方程） y(n) 3 y(n 1) 2 y(n 2) 0，y (0) 1, y (2) 2 解特点：无特解项 y (n) 的 n取值从 ~
2 3 2 0 得1 1, 2 2 y(n) C1 C2 2n 即： C1 0 1 C1 C2 得： C2 1 2 C1 2C2
n ~ 1
yh '(n) ~ 1 yh (n) : n 0 ~ D(n) : n 0 ~ D '(n) 0 ~ 1 用 y (0)…… y ( N 1) y(1) …… y ( N ) y(n) [ yh (n) D(n)]u(n) yh '(n)u(n 1)
1=C1+C2 2=C1+2C2+4
解得C1=4，C2=-3，故 y(n) 4 3 2 2 n 2
n
n n
n
当n≤-1时 y(n) C1 1 C2 2 3 1 C1 C2 2 2 C1 3 故 解得 C C 2 2 9 C2 3 2 1 4
§7.4 线性常系数差分方程的求解

•二、系统的概念
• 一般而言，系统(system)是指若干相互关联的事物组合 而成具有特定功能的整体。
• 如手机、电视机、通信网、计算机网等都可以看成系统。 它们所传送的语音、音乐、图象、文字等都可以看成信号。
• 信号的概念与系统的概念常常紧密地联系在一起。
• 信号的产生、传输和处理需要一定的物理装置，这样的 物理装置常称为系统。
1.3 信号的基本运算
• 一、信号的＋、－、×运算 • 两信号f1(·) 和f2 (·)的相+、－、×指同一时刻
两信号之值对应相加减乘。如
信号的概念与系统的概念常常紧密地联系在一起。 对于连续系统,设其最右端积分器的输出x(t); 相应地，对于离散信号，也有能量信号、功率信号之分。 若信号f (t)的功率有界，即P <∞ ,则称其为功率有限信号，简称功率信号。 时间和幅值都为连续的信号称为模拟信号。 可见，引入冲激函数之后，间断点的导数也存在。 确定信号与随机信号波形 解：图中有两个积分器，因而系统为二阶系统。 高度无穷大，宽度无穷小，面积为1的对称窄脉冲。 对于连续系统,设其最右端积分器的输出x(t); 若信号不能用确切的函数描述，它在任意时刻的取值都具有不确定性，只可能知道它的统计特性，如在某时刻取某一数值的概率，这类信号称为 随机信号或不确定信号。 为传送消息而装设的全套技术设备（包括传输信道）。 解析描述——建立差分方程 （2） yzs(t) = | f (t)|， yzi(t) = 2 x(0) 若系统既是齐次的又是可加的，则称该系统是线性的，即
• 三、冲激函数的性质 • 四、序列δ(k)和ε(k) • 1.5 系统的描述
• 一、系统的数学模型 • 二、系统的框图表示 • 1.6 LTI系统分析方法概述

哈尔滨工业大学自动化测试与控制系
信号与系统—signals and systems
2．离散时间系统与连续时间系统的对比 离散
连续
数学模型
差分方程
微分方程
时域求解方法
卷积和
卷积
变换域
Z变换、傅氏、离散正交变换、系 傅氏、拉氏、系统函数 统函数
精度高、可靠性好、 重量体积小、便于大规模集成
无此优点
一维、二维系统
哈尔滨工业大学自动化测试与控制系
信号与系统—signals and systems
⑥正弦信号 x(n)sin0 余弦信号 x(n)cosn0
1·
-5 -10
5 10 n
-1·
周期：
1）
若
2
0
为正整数，T
2)
2
若 0
为有理数，T k •
2 0
2 ,k0为使2
0
0
= 0.1 T=20
为正整数的最小正整数
1/E
1/E
-2
哈尔滨工业大学自动化测试与控制系
信号与系统—signals and systems
4. 微分方程 差分方程ห้องสมุดไป่ตู้
dy(t)Ay(t)B(xt) y (n 1 ) a(n y ) b(n x )
dt
d(yt)y[n (1)T]y(nT )
T应足够小
dt
T
y [(n 1 )T ]y(n T )A y(n T ) B x(n T )
信号与系统—signals and systems
③N阶线性常系数差分方程一般形式
N
M
aiy(ni) bjx(ni) 后向差分形式
i0
j0

0
1 e L e e ed t 0 α s α s 0
α t α t st

α s t

σ α
st L t t e d t 1 全s域平面收敛
L t t t t e d t e 0 0
T 1 2 T 1 1 2
注意！
傅立叶级数与傅立叶系数的联系与区别
指数形式傅立叶级数的傅里叶系数
jn1t 称为指数形式 f ( t ) Fne 的傅立叶级数 n


1 F (n 1) Fn T 1
T1 2 T 1 2
f (t )e
jn1t
dt , n (,)



L t t te d
st 0
1 st t de s 0
1 1 st 1 e 2 s s 0 s n 2 2 21 2 2 L t L t 2 3 s ss s n 3 3 2 32 6 3 L t L t 3 4 s ss s n! n 所 以 L t n1 s
Ee
t ( )2
E e
-(
ut
傅立叶变换特性主要内容
对称性质 奇偶虚实性 时移特性
线性性质 尺度变换性质 频移特性
微分性质
时域积分性质
第三章
•时域卷积定理
若 f t F , f t F 1 1 2 2

则 f t f t F F 1 2 1 2

定义：
单边拉氏变换、双边、收敛域、常用函数的拉氏变换
拉氏变换的性质

2.积分 信号的积分是指信号在区间(-∞，t)上的积分。可表示为
t
y(t)
f()df( 1)(t)
1.2.3 信号的相加、相乘及综合变换 1.相加
信号相加任一瞬间值，等于同一瞬间相加信号瞬时值的和。即
y (t)f1 (t)f2 (t) ...
1.2.3 信号的相加、相乘及综合变换 2.相乘
信号相乘任一瞬间值，等于同一瞬间相乘信号瞬时值的积。即
离散时间系统是指输入系统的信号是离散时间信号，输出也是离散 时间信号的系统，简称离散系统。如图连续时间系统与离散时间系统(b) 所示。
1.3.1 系统的定义及系统分类 2. 线性系统与非线性系统
线性系统是指具有线性特性的系统，线性特性包括齐次性与叠加性。线 性系统的数学模型是线性微分方程和线性差分方程。
2.1.2 MATLAB语言的特点
1、友好的工作平台和编程环境 2、简单易用的程序语言 3、强大的科学计算机数据处理能力 4、出色的图形处理功能
1、友好的工作平台和编程环境
MATLAB由一系列工具组成。这些工具方 便用户使用MATLAB的函数和文件，其中 许多工具采用的是图形用户界面。
新版本的MATLAB提供了完整的联机查询、 帮助系统，极大的方便了用户的使用。简 单的编程环境提供了比较完备的调试系统， 程序不必经过编译就可以直接运行，而且 能够及时地报告出现的错误及进行出错原 因分析。
y (t)f1 (t) f2 (t) ...
1.2.3 信号的相加、相乘及综合变换 3.综合变换 在信号分析的处理过程中，通常的情况不是以上某种单一信号的运算，往
往都是一些信号的复合变换，我们称之为综合变换。
1.3 系统
1.3.1 系统的定义及系统分类

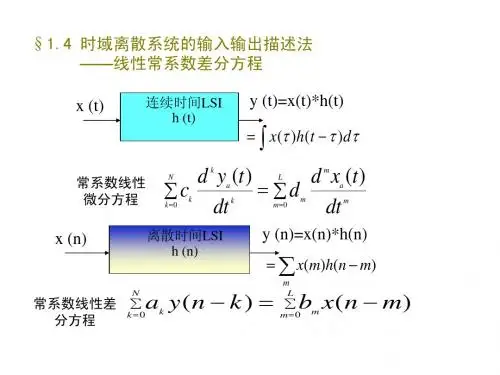
差分方程齐次解的一般形式
（实用版）
目录
1.差分方程的定义与基本概念
2.齐次差分方程的解法
3.差分方程齐次解的一般形式
4.应用实例与结论
正文
一、差分方程的定义与基本概念
差分方程是一种特殊的微分方程，它的研究对象是离散函数。

差分方程在数学、物理、生物、经济等领域有广泛的应用。

它是描述离散系统运动的一种有效方法。

二、齐次差分方程的解法
对于齐次差分方程，我们可以通过特征方程的方法求解。

特征方程的根即为齐次差分方程的通解。

具体步骤如下：
1.确定差分方程的特征方程
2.求解特征方程的根
3.根据特征方程的根，写出齐次差分方程的通解
三、差分方程齐次解的一般形式
设齐次差分方程为：a_n = b_n，其中 a_n 和 b_n 为已知数列。

根据特征方程求解得到的通解可表示为：
a_n = c * r^n，其中 c 为任意常数，r 为特征方程的根。

四、应用实例与结论
通过求解齐次差分方程，我们可以研究许多实际问题。

例如，在生物学中，可以用差分方程描述种群的增长；在经济学中，可以用差分方程描述货币供应和需求等。

总结：差分方程齐次解的一般形式为 a_n = c * r^n，其中 c 为任意常数，r 为特征方程的根。