网络计划优化案例 工期优化
- 格式:doc
- 大小:537.00 KB
- 文档页数:5


简述网络计划工期优化的步骤:工期简述步骤优化计划工期优化步骤顺序简述工期优化的步骤工期优化步骤是什么篇一:简述资源有限、工期最短的网络计划优化方法简述资源有限、工期最短的网络计划优化方法摘要:实践证明:采用网络计划技术,对于缩短工期,提高工效,降低成本,合理使用资源等方面,都能取得良好效果。
网络计划的资源优化有两类,一是“资源有限,工期最短”优化;二是“工期固定,资源均衡”优化,本文主要介绍第一类的优化方法。
1.引言项目在实施阶段有三个目标:一是高质量;二是不能超过投资总额;三是短工期。
项目的三大目标组成了一个完整的目标系统,三者之间的关系是相互制约、相互影响的。
比如,缩短工期往往会引起成本上升和质量下降;一个质量要求很高的项目在成本和工期上则不可能要求达到最优。
为适应大规模生产的发展和关系复杂的现代科学研究的需要,国内外陆续采用的以网络图为基础的计划管理新方法,即网络计划技术。
2.网络计划网络计划技术,也称网络分析法,它是在计划管理中通过网络图的形式,用来安排工程计划,控制施工进度和费用,使其达到预定目标的一种科学管理方法。
网络也是整个施工计划的模型。
其基本原理是:首先应用网络图的形式来表示计划中各项工作的先后顺序和相互关系;其次是通过计算找出计划中的关键工作和线路,在计划执行过程中进行有效的控制和监督,保证合理地使用人力、物力、财力来完成目标任务。
3.网络计划的优化3.1.含义网络计划的优化,就是根据编制计划的要求,在一定约束条件下,通过利用时差,不断改善计划方案,要求周期最短,费用最小,资源利用充分有效及切实可行的最优计划方案。
通过逐次优化,时差逐次减少,以至大部或全部消失。
然后根据优化的结果,最后做出决策。
网络计划优化工作是多方面的,有组织、技术方面,也有经济方面;有定性的,也有定量的。
例如:在资源基本保证的条件下,如何做到既保证工期又尽量节省资源:在资源有限条件下,如何尽量缩短工期:在工期不变的条件下,如何合理利用资源;在缩短工期的同时,如何保证成本最低等等,都属于网络计划优化的具体内容。


网络计划优化案例试题及答案一、试题。
某工程的网络计划如下图所示,箭线上方括号外为工作名称,括号内为正常持续时间(天),箭线下方括号外为直接费用率(千元/天),括号内为最短持续时间(天)。
工程间接费用率为0.8千元/天,正常工期时的间接费用为16千元。
试进行工期优化,求出最低工程费用及其相应的工期。
[此处应插入网络计划图,图中节点用数字表示,例如1 2之间有工作A,正常持续时间为6天,直接费用率为0.5千元/天,最短持续时间为4天等类似表示]二、答案及解析。
1. 计算各工作的直接费用率和可压缩时间。
对于工作A,正常持续时间D_A=6天,最短持续时间d_A=4天,直接费用率C_A=0.5千元/天,可压缩时间Δ t_A=6 4=2天。
按照同样的方法计算其他工作的相关参数。
2. 找出关键线路并计算总工期和总费用。
通过计算(可采用标号法等计算关键线路的方法),找出关键线路,假设关键线路为1 2 3 4,总工期T = 18天。
总直接费用C_d(假设所有工作按正常持续时间计算直接费用之和),总间接费用C_i=0.8×18 + 16 = 30.4千元,总费用C = C_d+C_i。
3. 进行工期优化。
选择直接费用率最小的关键工作进行压缩。
假设在关键线路上工作A的直接费用率最小。
每次压缩Δ t = min{Δ t_A,Δ t_B,·s}(其中A,B,·s为关键工作),并且要考虑压缩后是否会改变关键线路。
压缩工作A一天,此时总工期变为T'=17天。
重新计算总费用:总直接费用增加0.5×1 = 0.5千元。
总间接费用减少0.8×1 = 0.8千元。
总费用C'=C 0.8+0.5。
继续按照上述方法进行压缩,直到不能再压缩为止(即再压缩会使直接费用增加超过间接费用减少量)。
4. 确定最低工程费用及其相应工期。
通过不断的计算和优化,最终得到最低工程费用及其对应的工期。




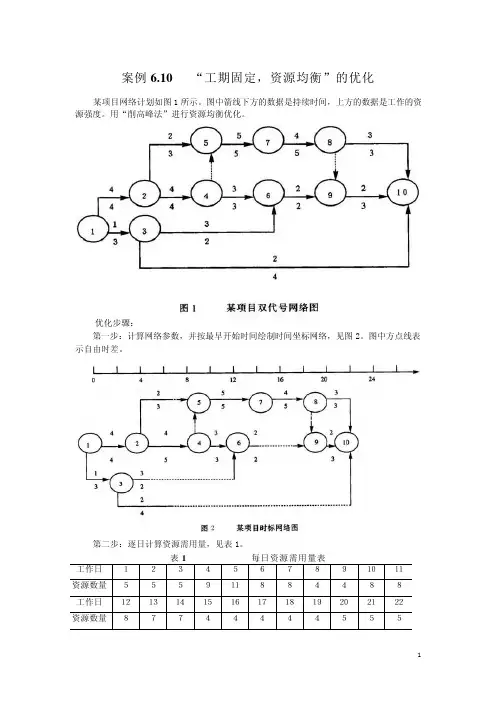
案例6.10 “工期固定,资源均衡”的优化某项目网络计划如图1所示。
图中箭线下方的数据是持续时间,上方的数据是工作的资源强度。
用“削高峰法”进行资源均衡优化。
优化步骤:第一步:计算网络参数,并按最早开始时间绘制时间坐标网络,见图2。
图中方点线表示自由时差。
第二步:逐日计算资源需用量,见表1。
表1 每日资源需用量表工作日1234567891011资源数量555911884488工作日1213141516171819202122资源数量87744444555第三步:确定资源限量。
用表1中的最大值减去一个单位量作为资源限量。
由于峰值是第5天的11,故资源限量为:R=11-1=10第四步:分析资源用量的高峰并进行调整。
根据表1中的资源数量,可以确定资源超限的状况。
其中,第5天的资源需要量是11,超过R=10的限量。
由图2可见,第5天正在进行的工作有:2-5、2-4、3-6、3-10,分别计算其时间差值△T i-j:△T2-5=TF2-5-(T h-ES2-5)=2-(5-4)=1△T2-4=TF2-4-(T h-ES2-4)=0-(5-4)= -1△T3-6=TF3-6-(T h-ES3-6)=12-(5-3)=10△T3-10=TF3-10-(T h-ES3-10)=15-(5-3)=13可见,工作2-5、3-6、3-10都可以移动,其中工作3-10的时间差值最大,故优先将该工作向右移动2天(即第5天之后开始) ,见图3 (注意图中方点线的位置与图2中的差别)。
重新计算每日资源需要量,见表2。
表2 第一次调整后每日资源需用量表工作日1234567891011资源数量55579886688工作日1213141516171819202122资源数量87744444555根据第一次调整情况,观察其峰值变化状况,若在其他时段出现超过R的情况时,则重复第四步,直至不超过R为止。
本例中,工作3-10调整后,其他时段未出现超过峰值 (R=10) 的情况。

一、工期优化示例已知某工程双代号网络计划如图1所示,图中箭线下方括号外数字为工作的正常持续时间,括号内数字为最短持续时间;箭线上方括号内数字为优选系数,该系数综合考虑质量、安全和费用增加情况而确定。
选择关键工作压缩其持续时间时,应选择优选系数最小的关键工作。
若需要同时压缩多个关键工作的持续时间时,则它们的优选系数之和(组合优选系数)最小者应优先作为压缩对象。
现假设要求工期为15,试对其进行工期优化。
图1初始网络计划(1)根据各项工作的正常持续时间,用标号法确定网络计划的计算工期和关键线路,如图2所示。
此时关键线路为①—②—④—⑥。
图2初始网络计划中的关键线路(2)由于此时关键工作为工作A、工作D和工作H,而其中工作A酌优选系数最小,故应将工作A作为优先压缩对象。
(3)将关键工作A的持续时间压缩至最短持续时间3,利用标号法确定新的计算工期和关键线路,如图3所示。
此时,关键工作A被压缩成非关键工作,故将其持续时间3延长为4,使之成为关键工作。
工作A恢复为关键工作之后,网络计划中出现两条关键线路,即:①—②—④—⑥和①—③—④—⑥,如图4所示。
图3工作A压缩至最短时间时的关键线路图4第一次压缩后的网络计划(4)由于此时计算工期为18,仍大于要求工期,故需继续压缩。
需要缩短的时间:△T=18-15=3。
在图5所示网络计划中,有以下五个压缩方案:①同时压缩工作A和工作B,组合优选系数为:2+8=10;②同时压缩工作A和工作E,组合优选系数为:2+4=6;③同时压缩工作B和工作D,组合优选系数为:8+5=13;④同时压缩工作D和工作E,组合优选系数为:5+4=9;⑤压缩工作H,优选系数为10。
在上述压缩方案中,由于工作A和工作E的组合优选系数最小,故应选择同时压缩工作A和工作E的方案。
将这两项工作的持续时间各压缩1(压缩至最短),再用标号法确定计算工期和关键线路,如图5所示。
此时,关键线路仍为两条,即:①—②—④—⑥和①—③—④—⑥。

第十节网络计划优化一、工期优化所谓工期优化,是指网络计划的计算工期不满足要求工期时,通过压缩关键工作的持续时间以满足要求工期目标的过程。
通过压缩关键工作的持续时间来达到优化目标。
在工期优化过程中,此外,网络计划的工期优化可按下列步骤进行:(1)确定初始网络计划的计算工期和关键线路。
(2)按要求工期计算应缩短的时间△T:△T=Tc-Tr式中:Tc——网络计划的计算工期;Tr——要求工期。
(3)选择应缩短持续时间的关键工作。
选择压缩对象时宜在关键工作中考虑下列因素:1)缩短持续时间对质量和安全影响不大的工作;2)有充足备用资源的工作;3)缩短持续时间所需增加的费用最少的工作。
(4)将所选定的关键工作的持续时间压缩至最短,并重新确定计算工期和关键线路。
若被压缩的工作变成非关键工作,则应延长其持续时间,使之仍为关键工作。
(5)当计算工期仍超过要求工期时,则重复上述(2)~(4),直至计算工期满足要求工期或计算工期已不能再缩短为止。
(6)当所有关键工作的持续时间都已达到其能缩短的极限而寻求不到继续缩短工期的方案,但网络计划的计算工期仍不能满足要求工期时,应对网络计划的原技术方案、组织方案进行调整,或对要求工期重新审定。
二、费用优化费用优化又称工期成本优化,是指寻求工程总成本最低时的工期安排,或按要求工期寻求最低成本的计划安排的过程。
1.费用与时间的关系在工程项目施工过程中.完成一项工作通常可以采用多种施工方法和组织方法,而不同的施工方法和组织方法,又会有不同的持续时间和费用。
由于一项工程项目往往包含许多工作,所以在安排工程进度计划时,就会出现许多方案。
进度方案不同,所对应的总工期和总费用也就不同。
为了能从多种方案中找出总成本最低的方案,必须首先分析费用与时间之间的关系。
(1)工程费用与工期的关系。
工程总费用由直接费和间接费组成。
直接费由人工费、材料费、机械使用费、措施费等组成。
施工方案不同,直接费也就不同;如果施工方案一定工期不同,直接费也不同。
简述资源有限、工期最短的网络计划优化方法摘要:实践证明:采用网络计划技术,对于缩短工期,提高工效,降低成本,合理使用资源等方面,都能取得良好效果。
网络计划的资源优化有两类,一是“资源有限,工期最短”优化;二是“工期固定,资源均衡”优化,本文主要介绍第一类的优化方法。
1.引言项目在实施阶段有三个目标:一是高质量;二是不能超过投资总额;三是短工期。
项目的三大目标组成了一个完整的目标系统,三者之间的关系是相互制约、相互影响的。
比如,缩短工期往往会引起成本上升和质量下降;一个质量要求很高的项目在成本和工期上则不可能要求达到最优。
为适应大规模生产的发展和关系复杂的现代科学研究的需要,国内外陆续采用的以网络图为基础的计划管理新方法,即网络计划技术。
2.网络计划网络计划技术,也称网络分析法,它是在计划管理中通过网络图的形式,用来安排工程计划,控制施工进度和费用,使其达到预定目标的一种科学管理方法。
网络也是整个施工计划的模型。
其基本原理是:首先应用网络图的形式来表示计划中各项工作的先后顺序和相互关系;其次是通过计算找出计划中的关键工作和线路,在计划执行过程中进行有效的控制和监督,保证合理地使用人力、物力、财力来完成目标任务。
3.网络计划的优化3.1.含义网络计划的优化,就是根据编制计划的要求,在一定约束条件下,通过利用时差,不断改善计划方案,要求周期最短,费用最小,资源利用充分有效及切实可行的最优计划方案。
通过逐次优化,时差逐次减少,以至大部或全部消失。
然后根据优化的结果,最后做出决策。
网络计划优化工作是多方面的,有组织、技术方面,也有经济方面;有定性的,也有定量的。
例如:在资源基本保证的条件下,如何做到既保证工期又尽量节省资源:在资源有限条件下,如何尽量缩短工期:在工期不变的条件下,如何合理利用资源;在缩短工期的同时,如何保证成本最低等等,都属于网络计划优化的具体内容。
3.2.研究意义绘制网络图、计算时间参数和确定关键路线,仅仅是网络计划的初步,只能得到一个初始的计划方案。
案例6.9 “资源有限,工期最短”优化某项目时间坐标网络计划如图1所示。
图中方点线表示自由时差;箭线下方标注的数据为相应工作的持续时间,上方是工作所需人力资源强度(人/天) 。
若每天只有9个工人可供使用,如何安排各工作的最早开始时间才能使工期最短。
优化步骤:第一步:计算每日资源需用量。
计算结果如表1所示。
第二步:逐日检查资源需求量并与资源限量比较。
由表1可见,第一天资源需要量就超过了可供资源量,必须进行工作最早开始时间的调整。
表1 每日所需人力资源数量表工作日12345678910资源数量13131313131377138工作日11121314151617181920资源数量8555565555第三步:分析资源超限的时段。
从第1~6天,资源需要量均为13,超出了资源限量,在这一时段内有工作1-2、1-3和1-4。
第四步:确定需要调整工作的顺序。
工作1-2、1-3和1-4有资源冲突,其网络参数如表2所示。
表2 超过资源限量的时段工作参数表工作代号i-jEFi-jLSi-j1—2801—3671—496将上述三项工作进行两两排列,组成不同方案,并计算其工期延长时间,计算结果见表3。
表3 △D i,j值计算表工作名称EFLS△D1-2△D1-3△D2-1△D2-3△D3-1△D3-211—4969221—2802131—36706由表3可见,将工作1-4置于1-3之后,工期未增加。
按此方案调整,并绘制新的网络计划,如图2所示(注意1-4的方点线的位置与图1中不同,表明此时1-4尚未开始)。
第五步:重复上述步骤。
根据第一次调整方案,逐日计算资源需求量,如表4所示。
表4 人力资源需求表工作日12345678910资源数量888888771313工作日11121314151617181920资源数量131010101065555可见,在第9天,资源需求超出限量,这时的工作有1-4、2-4、2-5、2-3,计算各方案的工期延长值,结果见表5。
某水利枢纽工程由大坝、电站、泄洪洞(底孔)和溢流表孔等建筑物组成。
为满足度汛要求,工程施工采取两期导流,一期工程施工泄洪底孔坝段(A )和溢流表孔坝段(B )。
某承包人承担了该项(一期工程)施工任务,并依据《水利水电工程标准施工招标文件》(2009年版)与发包人签订了施工合同。
合同约定:(1)签约合同价为4500万元,工期24个月,2011年9月1日开工,2011年12月1日截流。
(2)开工前,发包人按约定签约合同10%向承包人支付工程预付款,工程预付款的扣回与还清按sF F S F C A R )()(121--=计算,其中F 1=20%,F 2=90%。
(3)从第一个月起,按工程进度款5%的比例扣留工程质量保证金。
由承包人编制,并经监理人批准的施工进度计划如果2-1所示(单位:月,每月按30天计):图1-1施工进度计划图本工程在施工过程中发生以下事件:事件一:由于发包人未按时提供施工场地,造成了开工时间推迟,导致“初期围堰填筑”的延误,经测算“初期围堰填筑”要延至2012年1月30日才能完成。
承包人据此向监理人递交了索赔意向通知书,后经双方协商达成如下事项:(1)截流时间推迟到2012年2月1日;(2)“围堰加高”须在2012年5月30日(含5月30日)前完成;(3)完工日期不变,调整进度计划;(4)承包人依据工期—费用表(如表2所示),重新编制新的施工进度计划,并提交了赶工措施和增加的费用,上报监理人并批准。
的2012年3月份已完成工程量清单中“截流及基坑排水”的金额为245万元,“围堰加高”的金额为135万元,均含赶工增加费用。
事件三:结合现场及资源情况,承包人对新的施工进度计划进行了局部调整,A坝段采用搭接施工,其单代号搭接网络如图2-2所示:图1-2 A坝段施工进度单代号搭接网络图问题:1.根据原网络进度计划,分别指出“初期围堰填筑”和“围堰加高”的最早完成日期。
2.根据事件一,按增加费用最少原则,应如何调整施工进度计划?计算施工所增加的总费用。
第一节 网络计划优化网络计划的优化是指利用时差不断地改善网络计划的最初方案,在满足既定目标的条件下,按某一衡量指标来寻求最优方案。
华罗庚曾经说过,在应用统筹法时,要向关键线路要时间,向非关键线路要节约。
网络计划的优化按照其要求的不同有工期目标、费用目标和资源目标等。
一.工期优化当网络计划的计算工期大于要求工期时,就需要通过压缩关键工作的持续时间来满足工期的要求。
工期优化是指压缩计算工期,以达到计划工期的目标,或在一定约束条件下使工期最短的过程。
在工期优化过程中要注意以下两点: (1)不能将关键工作压缩成非关键工作;在压缩过程中,会出现关键线路的变化(转移或增加条数),必须保证每一步的压缩都是有效的压缩。
(2)在优化过程中如果出现多条关键路线时,必须考虑压缩公用的关键工作,或将各条关键线路上的关键工作都压缩同样的数值,否则,不能有效地将工期压缩。
工期优化的步骤:1.找出网络计划中的关键工作和关键线路(如用标号法),并计算出计算工期; 2.按计划工期计算应压缩的时间T ∆;p c T T T -=∆式中,c T — 网络计划的计算工期p T — 网络计划的计划工期3.选择被压缩的关键工作,在确定优先压缩的关键工作时,应考虑以下因素: (1)缩短工作持续时间后,对质量和安全影响不大的关键工作; (2)有充足的资源的关键工作;(3)缩短工作的持续时间所需增加的费用最少。
4.将优先压缩的关键工作压缩到最短的工作持续时间,并找出关键线路和计算出网络计划的工期;如果被压缩的工作变成了非关键工作,则应将其工作持续时间延长,使之仍然是关键工作;5.若已经达到工期要求,则优化完成。
若计算工期仍超过计划工期,则按上述步骤依次压缩其它关键工作,直到满足工期要求或工期已不能再压缩为止;6.当所有关键工作的工作持续时间均已经达到最短而工期仍不能满足要求时,应对计划的技术、组织方案进行调整,或对计划工期重新审订。
例1.已知网络计划如下图所示,箭线下方括号外为正常持续时间,括号内为最短工作历时,假定计划工期为100天,根据实际情况和考虑被压缩工作选择的因素,缩短顺序依次为B 、C 、D 、E 、G 、H 、I 、A ,试对该网络计划进行工期优化。
一、工期优化示例
已知某工程双代号网络计划如图1所示,图中箭线下方括号外数字为工作的正常持续时间,括号内数字为最短持续时间;箭线上方括号内数字为优选系数,该系数综合考虑质量、安全和费用增加情况而确定。
选择关键工作压缩其持续时间时,应选择优选系数最小的关键工作。
若需要同时压缩多个关键工作的持续时间时,则它们的优选系数之和(组合优选系数)最小者应优先作为压缩对象。
现假设要求工期为15,试对其进行工期优化。
图1 初始网络计划
(1)根据各项工作的正常持续时间,用标号法确定网络计划的计算工期和关键线路,如图2所示。
此时关键线路为①—②—④—⑥。
(①,5)(②,11)
(①,②,6)(④,11)
图2 初始网络计划中的关键线路
(2)由于此时关键工作为工作A、工作D和工作H,而其中工作A酌优选系数最小,故应将工作A作为优先压缩对象。
(3)将关键工作A的持续时间压缩至最短持续时间3,利用标号法确定新的计算工期和关键线路,如图3所示。
此时,关键工作A被压缩成非关键工作,故将其持续时间3延长为4,使之成为关键工作。
工作A恢复为关键工作之后,网络计划中出现两条关键线路,即:①—②—④—⑥和①—③—④—⑥,如图4所示。
(①,3)(③,10)
(①,6)(④,10)
图3 工作A压缩至最短时间时的关键线路
(①,4)(②,③,10)
(①,6)(④,10)
图4 第一次压缩后的网络计划
(4)由于此时计算工期为18,仍大于要求工期,故需继续压缩。
需要缩短的时间:△T=18 -15 = 3。
在图5所示网络计划中,有以下五个压缩方案:
①同时压缩工作A和工作B,组合优选系数为:2+8=10;
②同时压缩工作A和工作E,组合优选系数为:2+4=6;
③同时压缩工作B和工作D,组合优选系数为:8+5=13;
④同时压缩工作D和工作E,组合优选系数为:5+4=9;
⑤压缩工作H,优选系数为10。
在上述压缩方案中,由于工作A和工作E的组合优选系数最小,故应选择同时压缩工作A和工作E的方案。
将这两项工作的持续时间各压缩1(压缩至最短),再用标号法确定计算工期和关键线路,如图5所示。
此时,关键线路仍为两条,即:①—②—④—⑥和①—③—④—⑥。
(①,6)(④,9)
图5 第二次压缩后的网络计划
在图5中,关键工作A和E的持续时间已达最短,不能再压缩,它们的优选系数变为无穷大。
(5)由于此时计算工期为17,仍大于要求工期,故需继续压缩。
需要缩短的时间:△T2=17 -15 =2。
在图5所示网络计划中,由于关键工作A和E已不能再压缩,故此时只有两个压缩方案:
①同时压缩工作B和工作D,组合优选系数为:8+5=13;
②压缩工作H,优选系数为10。
在上述压缩方案中,由于工作H的优选系数最小,故应选择压缩工作H的方案。
将工作H的持续时间缩短2,再用标号法确定计算工期和关键线路,如图6所示。
此时,计算工期为15,已等于要求工期,故图6所示网络计划即为优化方案。
(①,6)(④,9)图6 工期优化后的网络计划。