当前位置：文档之家 › 自控理论 4-3对数坐标图

自控理论 4-3对数坐标图

  • 格式：ppt
  • 大小：11.56 MB
  • 文档页数：57

下载文档原格式

  / 57

合集下载

自动控制原理第4章

自动控制原理第4章

= cos(ωt ) + jsin (ωt )
j ( ±180° + q ⋅360° )
| G(s) H (s) | e
j∠G ( s ) H ( s )
= 1⋅ e
(q=0, 1, 2, …)
从而得出绘制根轨迹所依据的条件是 ① 幅值条件 幅值条件 |G(s)H(s)|=1 (4.7) ② 相角条件 ∠G(s)H(s)=arg［G(s)H(s)］=±180°+q·360° (q=0, 1, 2, …) (4.8) ± 实际上满足相角条件的任一点, 一定可以找到相应的可变参 数值, 使幅值条件成立。所以, 相角条件式(4.8)也是根轨迹的充 要条件。只要利用相角条件就可确定根轨迹的形状, 但利用幅 值条件才可以求得给定闭环极点所对应的增益 增益K。进行相角计 增益 算时, 规定正实轴方向为0°, 逆时针 逆时针方向为相角的正方向。 正
G( s) =
K (τs + 1) s(Ts + 1)
其中, τ＞T。 试大致绘出其根轨迹。 解 首先将开环传递函数化为如下标准形式:
零极点 形式
k (s + 1/τ ) G( s) = s( s + 1 / T )
第四章根 轨 迹 分析 式中, k=τK/T。系统有两个开环极点p1=0、p2=-1/T和一个开环零 点z1=-1/τ, 所以系统的根轨迹有两条分支。当k=0时, 两条根轨迹 从开环极点开始; 当k→∞时, 一条根轨迹终止于开环零点z1, 另 (2-1)=1条趋于无穷远处。并且根据开环零极点的位置, 可知实 轴上的(z1,p1)和(-∞, p2)区间为根轨迹的区段。系统的根轨迹图 如图4-3所示, 其中“×”表示开环极点, “○”表示开环零点。

自动控制原理所有定理2021精选PPT

自动控制原理所有定理2021精选PPT
滞后环节
状态空间分析设计方法
模型
§7.1 线性系统状态空间数学模型
基本概念及状态空间描述 由机理分析建立状态空间表达式 由微分方程建立状态空间表达式 由传递函数建立状态空间表达式 状态空间表达式与传递函数矩阵
分析方法
§7.2 系统状态空间运动分析
线性定常系统状态运动分析 矩阵指数函数
状态空间分析设计方法
稳定性 准确性 快速性
稳态准确性 动态准确性
稳态特性 动态特性
控制系统的数学模型
连续时间线性时不变系统 离散时间线性时不变系统
L 1 变换 微分方程
常见数 学模型
传递函数 频率特性
z 1 变换 差分方程
L变换
脉冲传递函数
Z变换
s j
zejT
离散系统频率特性
状态空间模型
离散状态方程
anc(n)an1c(n1)...a0cbmr(m)bm1r(m1)...b0r(t)
k p limG(s) s0
1 1 kp
kv lim sG (s) s0
1 kv
ka lim s 2G(s) s0
1 ka
稳定性分析
劳斯判据
根轨迹分析方法 1 8 0 0 根轨迹
广义根轨迹
D(s) f s,k 0 D(s) f s,k f1(s)kf2(s) 0
1k f2(s) f1 (s)
T s 1 T s 1
s积 分 滞 后 记 忆
常见的典型环节
5 振 荡 环 节 G ( s ) s 2 2n n 2 s n 2 T 2 s 2 1 2 T s 1
： 阻 尼 比 ， n T 1 :无 阻 尼 振 荡 频 率
6 延 迟 环 节 G (s ) e s

控制工程-典型环节的对数坐标图(Bode图)

控制工程-典型环节的对数坐标图(Bode图)

(
j
)


arctan
1
2T T 2
2
南华大学
第四章 系统的频率响应分析
特点：
转折频率：
TT
=1，T
=1
T
=
n
。
低频段T<<1,→ 0dB线；
高频段T>>1,→-40dB/dec 线。
L() 20 0 -20 -40 () 0
-90
-180
-40dB/dec
T

T

100 ω(rad/s)
南华大学
典型环节的对数坐标图
(1) 比例环节
对数幅频特性为：
G( j) K
L() 20lg G( j) 20lg K
L(ω)为常数是平行于横轴的一条直线。
对数相频特性为(ω)=0 ，与横轴重合。
L(ω )
20lgK
0 ω
(ω)
0 ω
第四章 系统的频率响应分析
南华大学
第四章 系统的频率响应分析
(3) 积分环节
对数幅频特性：
G( j ) 1 j
dB 20lg G( j)
40
L( ) 20 lg G( j ) 20 lg 1 20 lg 20
-20dB/dec
对数相频特性：
0.1 1 10
( ) 90
180 G
南华大学
(2) 惯性环节
对数幅频特性为：
G( j) 1 jT 1

L( ) 20lg G( j ) 20lg
1
20lg 1 T 2 2
1 T 2 2
对数相频特性： ( ) G( j ) arctan T

自动控制原理-4-2

自动控制原理-4-2

它的Bode图如图 图如图4.20。 它的 图如图 。
传递函数为k／ 的积分单元 的积分单元。 传递函数为 ／s的积分单元。它 的对数幅频特性函数只须把刚才 画的图象向上移动lgkB。所以它 画的图象向上移动 。 是通过ω=1，L=lgkB而斜率为 是通过 ， 而斜率为-1 而斜率为 的直线。也可以说是通过ω=k， 的直线。也可以说是通过 ， L=0的点而斜率为 的直线。如图 的点而斜率为-1的直线 的点而斜率为 的直线。 4.21。 。
《自动控制原理》 自动控制原理》
第四章 频率响应法
是正的， 是负的。 当k>1，对数幅频特性曲线 ，对数幅频特性曲线L(G)是正的，当k<1，L(G)是负的。当k=1，L(G)=0。 是正的 ， 是负的 ， 。
4.5 基本单元的频率特性函数 1．比例单元 ． 比例单元的传递函数为 G ( s ) = k 频率特性函数就是 G ( jω ) = k
L(G)图象的特征是通过原点 图象的特征是通过原点(µ=0，L=0)而 图象的特征是通过原点 ， 而 斜率为-1B／十倍频程 也就是 也就是-20dB／十倍 斜率为 ／十倍频程(也就是 ／ 频程)的直线 的直线。 频程 的直线。
3．惰性单元 ． 惰性单元的传递函数是
它的频率特性函数是 即
1 G ( jω ) = ω 2T 2 + 1 arg G ( jω ) = − arctgωT
为画图方便，现在把 点附近L(G)的准确值与两条渐近 为画图方便，现在把ω=1／T点附近 ／ 点附近 的准确值与两条渐近 线之间的误差∆L即 列于表4.3中 线之间的误差 即L(G)-Lapprox列于表 中，并绘成曲线如图 4.24。图4.24是一条通用的修正曲线，只须把修正曲线横坐标轴 是一条通用的修正曲线， 。 是一条通用的修正曲线 点与图4.23的P点重合，然后把修正曲线逐点叠加到 点重合， 的ω=1／T点与图 ／ 点与图 的 点重合 两条渐近线上，得到的就是准确的对数幅频特性图，如图4.25 两条渐近线上，得到的就是准确的对数幅频特性图，如图 所示。这样的作图方法是很简便的，但要注意修正曲线与对数 所示。这样的作图方法是很简便的， 幅频特性必须使用统一的比例尺才能叠加。 幅频特性必须使用统一的比例尺才能叠加。

自动控制原理知识点汇总

自动控制原理知识点汇总

自动控制原理总结第一章绪论技术术语1. 被控对象:是指要求实现自动控制的机器、设备或生产过程。

2. 被控量：表征被控对象工作状态的物理参量(或状态参量)，如转速、压力、温度、电压、位移等。

3. 控制器：又称调节器、控制装置，由控制元件组成，它接受指令信号，输出控制作用信号于被控对象。

4. 给定值或指令信号r(t)：要求控制系统按一定规律变化的信号，是系统的输入信号。

5. 干扰信号n(t)：又称扰动值，是一种对系统的被控量起破坏作用的信号。

6. 反馈信号b(t)：是指被控量经测量元件检测后回馈送到系统输入端的信号。

7. 偏差信号e(t)：是指给定值与被控量的差值，或指令信号与反馈信号的差值。

闭环控制的主要优点：控制精度高，抗干扰能力强。

缺点：使用的元件多，线路复杂，系统的分析和设计都比较麻烦。

对控制系统的性能要求:稳定性快速性准确性稳定性和快速性反映了系统的过渡过程的性能。

准确性是衡量系统稳态精度的指标，反映了动态过程后期的性能。

第二章控制系统的数学模型拉氏变换的定义:几种典型函数的拉氏变换1.单位阶跃函数1(t)2.单位斜坡函数3.等加速函数4.指数函数e-at5.正弦函数sin ωt6.余弦函数cos ωt7.单位脉冲函数(δ函数)拉氏变换的基本法则1.线性法则2.微分法则3.积分法则4.终值定理5.位移定理传递函数：线性定常系统在零初始条件下，输出信号的拉氏变换与输入信号的拉氏变换之比称为系统(或元部件)的传递函数。

动态结构图及其等效变换1.串联变换法则2.并联变换法则3.反馈变换法则4.比较点前移“加倒数”；比较点后移“加本身”。

5.引出点前移“加本身”；引出点后移“加倒数”梅森（S. J. Mason）公式求传递函数典型环节的传递函数1.比例(放大)环节2.积分环节3.惯性环节4.一阶微分环节5.振荡环节6.二阶微分环节第三章时域分析法二阶系统分析二阶系统的单位阶跃响应1.过阻尼ξ>1的情况：系统闭环特征方程有两个不相等的负实根。

自动控制理频域伯德图

自动控制理频域伯德图


Lω 20lg1 ＝0 dB
——低频渐近线为一条0dB的水平直线。
Lω 20lg 1 Tn ω
2

2 2
2ζ T ω
n
2
高频段，即ωTn>>1时
L() 20lg( Tn ) 40lg(Tn )
2 2
当ω增加10倍
ωTn 40 40lgωTn L() 40lg10
相频与ω无关，值为-90°且平行于横轴的直线。
L ( )
20 0
20 0.1 10
1

( )
0 90
0.1
1
10

3 微分因子
G jω jω
微分环节是积分环节的倒数，它们的 曲线斜率和相位移也正好相差一个负号。
L ( )
20
0
20
0.1 20
1
10

( )
90
L() 40lg Tn 40lg1 0(dB)
即高频渐近线是一条斜率为-40dB/dec的直线。 当 ωω 1 时
n
Tn
说明
ω ωn
1 Tn
为二阶系统(振荡环节)的转折频率。

。10
0
0.1
0.2 0. 3
L ( )
dB
-40dB/dec
0 .7 1
10
系统 的相频特性为 90 arctan arctan 2 10
0
W=0
90
0
W=1
W=10 W=无穷大
110.860
123.70
0 90

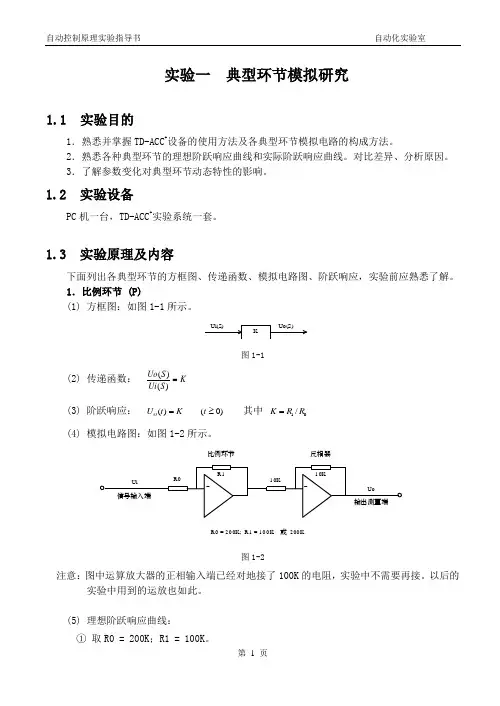
自控原理实验指导书_自动化

实验一 典型环节模拟研究1.1 实验目的1．熟悉并掌握TD-ACC +设备的使用方法及各典型环节模拟电路的构成方法。

2．熟悉各种典型环节的理想阶跃响应曲线和实际阶跃响应曲线。

对比差异、分析原因。

3．了解参数变化对典型环节动态特性的影响。

1.2 实验设备PC 机一台，TD-ACC +实验系统一套。

1.3 实验原理及内容下面列出各典型环节的方框图、传递函数、模拟电路图、阶跃响应，实验前应熟悉了解。

1．比例环节 (P)(1) 方框图：如图1-1所示。

图1-1(2) 传递函数：K S Ui S Uo =)()( (3) 阶跃响应：)0()(≥=t Kt U O 其中 01/R R K =(4) 模拟电路图：如图1-2所示。

图1-2注意：图中运算放大器的正相输入端已经对地接了100K 的电阻，实验中不需要再接。

以后的实验中用到的运放也如此。

(5) 理想阶跃响应曲线：① 取R0 = 200K ；R1 = 100K 。

② 取R0 = 200K ；R1 = 200K 。

2．积分环节 (I)(1) 方框图：如右图1-3所示。

图1-3(2) 传递函数：TSS Ui S Uo 1)()(=(3) 阶跃响应： )0(1)(≥=t t Tt Uo 其中 C R T 0=(4) 模拟电路图：如图1-4所示。

图1-4(5) 理想阶跃响应曲线：① 取R0 = 200K ；C = 1uF 。

② 取R0 = 200K ；C = 2uF 。

3．比例积分环节 (PI)(1) 方框图：如图1-5所示。

图1-5(2) 传递函数：TSK S Ui S Uo 1)()(+= (3) 阶跃响应： )0(1)(≥+=t tTK t Uo 其中01/R R K =；C R T 0=(4) 模拟电路图：如图1-6所示。

图1-6(5) 理想阶跃响应曲线：①取R0 = R1 = 200K；C = 1uF。

②取R0=R1=200K；C=2uF。

4．惯性环节 (T)(1) 方框图：如图1-7所示。

第五次课自动控制理论讲解

时,则对应得系统得开环频率特性为
2
G( jw)
K
1
w
j
w2
2
jw
1
j
w w1
1
j
w w3
它在wc处得相角为
(wc )
90
2 arctan
wc w1
2 arctan
wc w2
arctan
wc w3
90 (144 ~ 180) 144 18 108 ~ 144
即相位裕量 在 72 ~ 36 之间
★
三、闭环系统得性能分析 5、6-7 ★
w0 (jw)0 KG0 ( jw) 1 K
当v = 1时,闭环幅频 特性得零频值为
M (0) lim w0
KG0 ( jw) (jw)1 KG0 ( jw)
1
说明:0型与I型及以上系统零频值M(0)得差异,反映了它们跟随阶跃输
入时稳态误差得不同,前者有稳态误差,后者没有稳态误差。
2、频带宽度
即相位裕量 在 18 ~ 18 之间
[说明]:条件只就是必要而非充分得。
作业 pp、218-219: 5-13
第五章 频率响应法
• 5、1 频率特性 • 5、2 对数坐标图 • 5、3 极坐标图 • 5、4 用频率法辨识线性定常系统得数学模
型 • 5、5 奈奎斯特稳定判据 •• 55、、67 相频对域稳性定能性指分标析与时域性能指标之间得 • 5关、系7 频域性能指标与时域性能指标之间得
K
s(1 0.2s)(1 0.05s)
试求:K = 1时得 Kg 与 解 基于在wg处开环频率特性得相角为
(wg ) 90 arctan 0.2wg arctan 0.05wg 180

对数坐标图 公式

Dec Dec Dec Dec
− ∞...
0
−2 0.01
−1 0.1
0 1
1 10
2 100
log ω
ω
由于ω 以对数分度，所以零频率点在－∞处。
更详细的刻度如下图所示
ω
lg ω
ω lgω
１ 0.00 0
2 0.30 1
3 0.47 7
4 0.60 2
5 0.69 9
6 0.77 8
7 0.84 5
k =1 j =1 m2
m1
i =1
n1
− ∑ 20 lg (1 − ω 2Tl 2 ) + j 2ζ l Tl ω
l =1
n1 2ζ k Tk ω − v × 90° − ∑ tg −1Tk ω ϕ (ω ) = ∠K + ∑ tg −1τ iω + ∑ tg −1 1 − ω 2Tk2 i =1 k =1 k =1 m1 m2
幅值A(ω ) 1.00 对数幅值 20lgA(ω ) 0 1.26 2 0.79 -2 1.5 6 4 0.6 3 -4 2.0 0 6 0.5 0 -6 2.5 1 8 0.3 9 -8 3.1 6 10 0.3 2 -10 5.62 15 0.18 -15 10. 0 20 0.1 0 -20 100 40 0.0 1 -40 1000 60 0.001 -60 10000 80 0.0001 -80
L(ω) = 20log A(ω) = 20log = −20log ω,
π
L(ω ) / dB 40 20
1
ω
ω
1 10 100
− 20 − 40
ω =1, L(ω) = 0; ω =10, L(ω) = −20

自动控制原理与系统第4章 自动控制系统的频率分析法

它的对数相频特性和对数幅频特性间存在着确定的对应关系或者对于最小相位系统只需根据其对数幅频特性就能写出其传递函数45系统的闭环频率特性系统的开环传递函数gs为上式中系统的闭环传递函数s为其闭环频率特性闭环幅频特性由式420及可得若为自变量为应变量则可画出如图4419aa所示的闭环幅频特性和如图4419bb所示的闭环相频特性
在以上各式中，通常称
U(ω )——实频特性 V(ω )——虚频特性 M(ω )——幅频特性
() ——相频特性
G(jω )——
(4-1) (4–2) (4–3)
显然，幅频特性 相频特性
3.图形表示方式
图4-4 常见的二、三阶系统的幅相频率特性曲线
例如，有G1(jω )和G2(jω )两个环节串联，则其等效频率 若绘制极坐标图，其模M=M1M2，绘制起来十分麻烦，这是
②对数相频特性 为与横轴重合的水平直线。
图4-7 比例环节的伯德图
增设比例环节后，将使系统的 向上(或 向下)平移，而不会改变的 形状。对系统 将不产生任何影响。这是比例环节的一大特点。
2.积分环节 (1)传递函数
(2)频率特性 (3)对数频率特性
(4) ①对数幅频特性
由式(4-8)有
图4-8 积分环节的伯德图
4.5 系统的闭环频率特性
系统的开环传递函数G(s)为
上式中 系统的闭环传递函数Φ (s)为
其闭环频率特性
闭环幅频特性 由式(4-20)及
,可得
若ω 为自变量，
、
为应变量，则可画出如
图4-19（a）所示的闭环幅频特性和如图4-19（b）所
示的闭环相频特性。
图4-19 典型二阶控制系统的闭环频率特性
积分环节的对数幅频特性曲线 可表述为：在ω =1
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

(2) 将各环节的L(w),j(w)曲线画于对数坐标纸上 1) L1(w) = 20lg4 ≈12(dB)是幅值为12dB的水平线。 2) L2(w)是过ω=1, L(w)0dB,斜率为 -20dB/dec的直线。 3) L3(w)是转角频率为ω=0.5的惯性环节对数幅频曲线。 4) L4(w)是转角频率为ω=2的微分环节对数幅频曲线。 5) L5(w)是转角频率为ω=8的振荡环节对数幅频曲线。
惯性环节L(w) 1 ① G(s)= 0.5s+1
L(w)dB 40 26dB 20
100 ② G(s)= s+5
[-20]
0dB 0o -20 - 30o - 45o o -40 - 60 - 90o 0.1 0.2
ω
1
2
10 20
[-20]
100
5. 一阶微分环节 (Ts 1) L(w ) 20lg 1 (wT) 2 j (w ) tg -1wT 1 Ts 1与 两环节的 Bode 图关于 Ts 1 横轴成镜像对称 关系。
斜率 40 20 20
40
30
-20
20
17.5
10
-60 -80
0
-10
-60
-20
-30
-40 -1 10
10
0
10
1
图4-19 例4-6的幅频特性
1 7.5( s 1) 3 G( s) 1 s 2 1 s( s 1)[( ) s 1] 2 2 2
图4-19 例4-6的相频特性
j
290o w r w n 1 2
2
wn
0dB
L(w r ) 20 lg 2
0 1 ω
1
2
L(wn ) 20lg 2
8. 延迟（滞后）环节 (e TDS ) L(w ) 20lg1 0 (dB) j (w ) -wTD (rad ) -57.3wTD ( )
w 0 时 j 00 ; w w n 时 j -90 0 ; w 时 j -180 0
振荡环节
L(w)dB 40 20 0dB -20 -40
2 Kωn 4 G(s) 2 2 2 s 2ζωn s ωn s 2 0.2 2s 4
0 0.5时， L(wn ) 20lg2 0 0.5时， L(wn ) 0 0.5 1时， L(wn ) 0
相频特性 j(ω)
1)精确特性 2)渐近特性 3)误差修正 4) 相 角 曲 线模 板 ( jw ) G
1 1 jwT
j (w ) tg 1wT
j (w ) tg 1wT 在单对数纸上制作相角模板 : w j (w )
0 00 1 0.1 T 5.7 0 1 T 45 0 1 10 T 84.3 0 90 0
6)绘制各环节相频特性曲线 j1(w)～ j5(w)。
L2积分
L4一阶微分 L1比例
L5振荡 L3惯性
(3)将L1(w)～L5(w)叠加, 求得开环对数幅频曲线L(w) 当 ≤ 0.4 时,修正振荡环节 (4)将j1(ω)～ j5(ω)叠加, 求得开环对数相频特性曲 线j(ω)。
4(0.5 s 1) G( s) H ( s) s( 2 s 1)[( 0.125 s ) 2 0.05 s 1]
一阶微分L(w) ① G(s)= 0.5s+1
L(w)dB + 90o 40 + 60o + 45o 20 +30o 0dB 0o -20 -40 0.1 0.2
② G(s)= 0.3 (0.25s+0.1)
[+20]
[+20]
1 2 10 20
ω
100
1 6. 二阶振荡环节（ 2 2 ） T s 2Ts 1 1 L(w ) 20lg 2 -20lg (1 w 2T 2 ) 2 ( 2wT ) 2 T (jw ) 2 j2 wT 1 2wT ) j (w ) tg ( ) 2 2 1w T
1 T1 s G1 H 1 1 T2 s 1 T1 s G2 H 2 1 T2 s
三.开环系统Bode图的绘制方法
（一）环节曲线叠加法 【例4-5】系统开环传递函数为
4(0.5 s 1) G( s) H ( s) s( 2 s 1)[( 0.125 s ) 2 0.05 s 1]
试绘制其开环对数频率特性图。
解 (1)将开环频率特性按典型环节进行分解
4(0.5 s 1) G( s) H ( s) s( 2 s 1)[( 0.125 s ) 2 0.05 s 1]
j (w ) tg 1wT 1 (1) 低频 w 则 L(w ) -20lg1 0 低频渐近线 T 1 (2) 高频 w 则 L(w ) -20lg wT T 高频渐近线斜率为 - 20dB/dec 1 (3) 转角频率w T 精确值 L(w ) -20lg 2 -3.03 dB
0
积分环节L(w)
1 ① G(s)= s
L(w)dB 40 20 0dB -20
10 ② G(s)= s
1 ③ G(s)= 5s
[-20]
[-20] 1 2 10 20 [-20] ω 100
0.1 0.2
-40
3. 微分环节(s) L(ω)=20lg|jω|= 20lgω j(ω)= ∠jω= 900
4(0.5 s 1) G( s) H ( s) s( 2 s 1)[( 0.125 s ) 2 0.05 s 1]
1 1 1
wg
0.05w G ( jw ) tg 0.5w 90 tg 2w tg 1 (0.125w )2
0
（二）顺序斜率迭加法
步骤:
§4-3 对数坐标图
一.对数坐标图(Bode图)及其特点
1. Bode图的构成 对数幅频 L(w)=20lg │G(jw)H(jw)│=20lgA(w) 对数相频 j(ω)=∠G(jw)H(jw)
半对数坐标纸，如图4-7所示。
2. Bode图法的优点
(1) 对数分度利于扩展低频段，压缩高频段，
适合工程实际的需要。
2. 积分环节（1/s）
1 1 G ( jw ) 90 0 jw w
1 L(w ) 20 lg w 20 lg w j (w ) 1 90 jw
(dB ) (4 7)
幅频特性是斜率为－20dB/dec 的一条直线， 交0dB 线于w 1处。 相频特性是一条 －90 水平线。
1
1) 低频段 w
1 则 L(w ) -20lg1 0 低频渐近线斜率为 0 T 1 2) 高频段 w 则 L(w ) -20lg(wT) 2＝－40lg wT T 高频渐近线斜率为- 40dB/dec 1 3) 转角频率w w n T 对数相频 精确值 L(w n ) -20lg2
-20dB/dec;
(5) 每遇到一个转角频率就改变一次斜率;
0.35
(6) G ( jw ) tg
1
L(wn) 20lg 2 3 dB
w
0.5w 90 tg 0.5w tg 3 1 0.5w 2
0 1 1
wc -----剪切频率; wg ----- 相位穿越频率
1
二阶微分环节
G( s ) T s 2Ts 1
2 2 2 s 2 2wn s wn
w
2 n
1 wn T
G( jwn ) 290 , G( j0) 10 ,
o
G( j) o 180
对数幅频渐近曲线
L(w) [+40]
幅相曲线0<<0.707时有峰值：
ω 100
0.1 0.2
1
wn
2
10 20
[-40]
w r w n 1 2 1.92
2
20 lg M r 20 lg
1 2 1
2
8.14 dB
振荡环节再分析
L(w)dB
G (s)
1
2
S2
20 lg
2 2wnS wn 0＜＜0.5
2 wn K
2 1
10( s 3) G( s ) s( s 2)(s 2 s 2)
解 (1)化标准形式 (2)确定转角频率
1 7.5( s 1) 3 G( s) 1 s 2 1 s( s 1)[( ) s 1] 2 2 2
转角频率 斜率
2 40
2 20
3 20
( 3) 低 频 段 ： (w ) w 0 20 lg L
（4-8）
微分环节L(w) ① G(s)= s ② G(s)= 5s
L(w)dB 40 [+20] 20 0dB -20 -40
③ G(s)= 0.1s
ω 0.1 0.2 [+20] 1 2 [+20] 10 20 100
4. 惯性环节 （／Ts 1) 1 1 L(w ) 20 lg 20 lg 1 (wT ) 2 1 jw T
G( jw ) tg来自1w0.5w 90 tg 0.5w tg 3 1 0.5w 2
0 1 1
四.最小相位系统和非最小相位系统 (1)定义 ①最小相位系统
开环传递函数中，无右极点或右零点 (并且不具有延迟因子) 的系统; ②非最小相位系统
开环传递函数中，有右极点或右零点 (或具有延迟因子) 的系统。
7.5
w
20 lg 7.5 20 lgw