第三节 对数坐标图（伯德图）对数幅频特性曲线：前面提到过伯德图中对数幅频特性曲线的纵坐标采用()()20lg dB L w G j =w ，这是因为传递函数总可以分解为因子相乘、除的形式，从而其频率传递函数的模必然由相应各因子的模相乘、除得之，取其对数可将乘、除变为加、减而便于计算，至于前面的系数“20”则是沿用电信技术的增益表达式而来的，这样就使得()L w 的单位成为分贝“”。
dB 横坐标按自变量的常用对数进行刻度。
原因一方面可使变动范围得到扩展，在有限的图面上比起均匀刻度来能表现出更大的变动范围；另一方面，w w ()L w 中往往都含有lg 因子，采用自变量的常用对数刻度，可使自变w w量的对数曲线成为直线，便于绘制。
对数相频特性曲线：纵坐标()(w G j )w φ=∠均匀刻度；横坐标也按自变量的常用对数进行刻度。
w 若在横轴上取两点满足2110w w =，则距离为()2121lg lg lg lg101w w w w −===。
即横坐标每变化一个单位，相当于频率变化10倍，叫做一个“十倍频程”，用“”表示。
dec在标注横轴时，往往只标出w 的值，并不标出值。
lg w 这种计量坐标系称为半对数坐标系。
若212w w =，则距离为：()2121lg lg lg lg 20.301w w w w −=== 这表示横坐标每变化一个单位，相当于频率变化一倍，叫做一个“倍频程”，用“”表示。
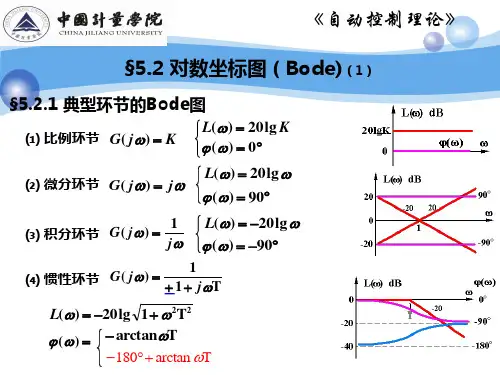
oct一、典型环节的对数坐标图1、比例环节（K ）()G jw K =（K 为常数） ()()20lg 20lg L w G jw K==（） dB ()()()011010Lw K K L w K L w ⎫==⎧⎪⎪>>⎨⎬⎪⎪<<⎩⎭()()0w G jw φ=∠=jw w()()()===−（dB）20lg20lg120lgL w G jw w w()20lg L w w =−()()011020L w w w L w ⎫==⎧⎪⎨⎬==−⎩⎪⎭()()90w G jw φ=∠=− ()L w 曲线为过（1，0）点，斜率为每十倍频程下降的一条直线，记为“20dB 20dB dec −”。
