第五章 导数(数学分析-河南师范大学,李文林)
- 格式:ppt
- 大小:643.00 KB
- 文档页数:24



高数大一第五知识点总结在大一学习高等数学的过程中,我们接触到了许多重要的知识点。
其中,第五章的内容是我们需要重点掌握和总结的。
本文将对第五章的知识点进行系统的总结和梳理。
一、导数导数是微积分的重要概念之一,它描述了函数在某一点的变化率。
在第五章中,我们学习了导数的定义和性质,以及如何求导。
1. 导数的定义导数的定义是函数的变化率,可以表示为f'(x)或者dy/dx,其中x是自变量,y是因变量。
导数的几何意义是函数曲线在某一点的切线斜率。
2. 导数的计算法则在求导的过程中,我们学习了许多计算导数的法则,如常数法则、幂函数法则、和差法则、乘积法则、商法则和复合函数求导法则。
这些法则可以帮助我们更快地求得函数的导数。
3. 高阶导数在第五章中,我们还学习了高阶导数的概念。
高阶导数表示对原函数的导数再求导。
我们可以通过一阶导数的法则来求得高阶导数。
二、微分微分是导数的另一种表达形式,它更侧重于函数在某一点的近似线性变化。
1. 微分的定义微分的定义是近似变化量的线性函数,可以表示为dy=f'(x)dx。
其中dx表示自变量的增量,dy表示函数值的增量。
2. 微分的计算法则我们可以利用导数的计算法则来求得微分,并且通过微分可以近似计算函数在某一点的值。
这使得我们可以在计算中方便地使用微分来替代原函数。
三、应用问题在学习高等数学的过程中,我们也需要将所学的知识应用到实际问题中,第五章的应用问题就是我们要重点关注的内容。
1. 几何应用问题在几何应用问题中,我们需要利用导数的概念和公式来解决与曲线相关的问题,如切线方程、法线方程、曲率等。
2. 最值问题最值问题在数学中也是非常常见的一类问题,通过求导和解方程可以求得函数的极值点,从而解决最值问题。
3. 实际应用问题除了几何和最值问题,我们还会遇到很多实际应用问题,如速度、加速度、优化问题等。
这些问题需要我们将数学知识与实际问题相结合,进行建模和求解。
总结:第五章的知识点涵盖了导数、微分和应用问题,这些内容对于我们理解和掌握高等数学的基本概念和方法非常重要。

高数知识点总结大一第五章第五章:高数知识点总结在大一学习高等数学时,第五章可能是最具挑战性的章节之一。
这一章主要介绍了导数和微分的概念与运算,它们是解决数学问题、理解和应用自然现象中的数学工具。
本文将对该章的重要知识点进行总结,以帮助读者更好地理解和掌握这些概念。
1. 导数的定义与几何意义导数是函数在某一点的变化率,用数学符号表示为f'(x)或dy/dx。
它描述了函数图像在某点的切线斜率,可以用来确定函数的极值、函数图像的形态、速度、加速度等概念。
当函数连续可导时,导数存在且唯一。
2. 导数的基本运算法则导数的基本运算法则包括常数法则、幂法则、和差法则、乘法法则、商法则等。
这些法则可以简化导数的计算,帮助我们更便捷地求解导数。
3. 高阶导数与Leibniz符号高阶导数是指对导数进行多次求导的结果。
例如,f''(x)表示对f'(x)再求导的结果,称为f(x)的二阶导数。
Leibniz符号可以简化高阶导数的书写,例如,f'(x)可以表示为dy/dx。
4. 微分与微分的几何意义微分是导数的另一种表达形式,表示函数在某一点的增量与自变量的增量之间的关系。
微分可以用来确定函数图像的局部线性近似,从而可以估计函数在某一点的近似值。
微分也常用于求解极值和优化问题。
5. 高阶导数与函数的性质通过高阶导数,我们可以了解函数的更多性质。
例如,f''(x)>0表示函数f(x)在某区间上是凸函数,f''(x)<0表示函数f(x)在某区间上是凹函数。
高阶导数还可以用于求解曲线的凹凸性、拐点、拐点类型等问题。
6. 隐函数与求导有些函数不能直接表示为y=f(x)的形式,而是通过方程关联在一起。
这样的函数称为隐函数。
通过隐函数求导,我们可以推导出一个方程中的两个变量之间的关系式。
7. 参数方程与求导参数方程是用参数表示的函数形式,它可以描述一条曲线或曲面。


导数的运算【学习目标】1.娴熟掌握基本初等函数的导数公式,掌握导数的四则运算法例;2.能利用给出的基本初等函数的导数公式和导数的四则运算法例求简单函数的导数【自主学习】1.基本初等函数的导数公式是什么?2.幂函数与指数函数的求导公式的差别是什么?3.导数的运算法例及推论是什么?4.求导法例和公式的构造是灵巧进行求导运算的前提条件,当函数分析式较为复杂时,应怎么做?当函数分析式不可以直接用公式时,应怎么做?【自主检测】1. 设曲线y x 1在点 (3,2) 处的切线与直线ax y 1 0 垂直,则a.x1 2. 已知曲线y x 23lnx的一条切线的斜率为1, 则切点的横坐标为.42【典型例题】例 1.依据基本初等函数的导数公式和导数运算法例,求以下函数的导数.(1)y x32x 3;( 2)y11x11 x(3)y sin x ln x ;( 4)y x;x1 ln x .4(5)y( 6)y (2 x25x1) e x;1ln x(7)y sin x cos x x21 cos x sin x(8) yx【讲堂检测】2x 2的导数是()1. 函数y2x21(A)4x x2 1 8x 34x x 2 1 4x 2 yx 23(B)y31x21(C)y 2x x218x3(D)y4x x 2 1 4x x 23x 23 112.若直线 y x b 为函数 y 1图象的切线 , 求 b=_________和切点坐标为 ___________. x3.已知曲线 C:y = 3x4- 2x3-9x2+ 4,求曲线 C上横坐标为 1 的点的切线方程 ______________.4.求过曲线 y=cosx 上点 P(3,1)的切线的直线方程 . 2【总结提高】1.娴熟掌握基本初等函数的导数公式;2.掌握导数的四则运算法例;3.能利用给出的基本初等函数的导数公式和导数的四则运算法例求简单函数的导数.。
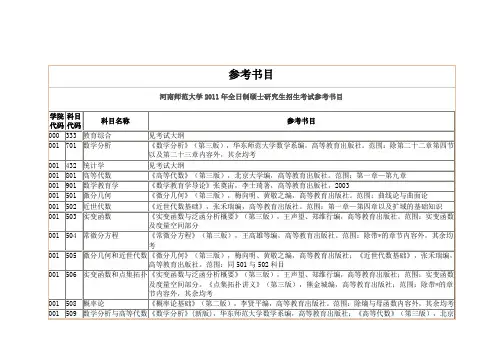

第1页,共2页2018年攻读硕士学位研究生入学考试试题科目代码与名称:611数学分析 适用专业或方向:数学、统计学 浜考试时间:3小时 满分:150分试题编号:A 令(必须在答题纸上答题,在试卷上答题无效,答题纸可向监考老师索要) (16分,每小题8分)求下列极限:二. (16分)证明当 x>\ 时有\fx\nx < x-\.三. (16分)设/(Z )在SM ]上连续,在(。
,厶)内可导,证明存在使得 2貝/(幻-/(。
))=(屏-/)♦«)四. (17分)设{々〃}单调递减趋于0,且对一切自然数〃有£(印-%)《1,求收k=\n=\敛,且d"〃=1五. (17分)证明£—— 在[丄1]上一致收敛.〃=]l + x + x~+ •・・ + •¥ 2六. (17 分)求曲线积分 / = £(-工3 + e> + sin x )dx + (A >>2 + xe v-cos y )dy ,其中《是 正向闭单位圆周. 七.(17分)1)lim ,002)第2页,共2页设/(x,y,z )具有二阶连续的偏导数,令z = f{xy,-,x )求 y八. (17 分)求 jjj (x + y + z)dxdydz ,其中/是球体x 2+y 2 +z 2<x + y + z.VK. (17 分)设函数/(对在(-00,+00)±连续,且 lim/(/(%)) = 00,证明 lim/(x) = oo.X->00x —>oo。

高数大一知识点总结第五章第五章是高等数学中的重要章节,主要介绍了微分学的基本概念和相关的方法。
本文将对第五章的知识点进行总结,包括导数、微分和应用等内容。
1. 导数导数是微分学的基本概念,表示函数在某一点上的变化率。
它的定义为函数f(x)在点x处的导数等于该点处的切线斜率。
导数可以通过求导的方式来计算,常用的求导法则包括常数法则、幂函数法则、和差法则、乘积法则和商法则等。
导数有很多重要的应用,例如可以用来求函数的极值、判断函数的单调性以及进行函数的图像绘制等。
此外,在物理学和经济学中,导数也经常用于解释实际问题和推导相关公式。
2. 微分微分是导数的一种表达形式,它表示函数在某一点上的变化量与自变量的变化量之间的关系。
微分可以用来近似计算函数的变化量,其计算公式为dy=f'(x)dx。
其中,dy表示函数的微分,f'(x)表示函数f(x)在点x处的导数,dx表示自变量的微小变化量。
微分可用于求函数的局部线性近似、计算函数的微小变化量以及推导相关公式等。
在实际应用中,微分还常常用于优化问题的求解,例如求函数的最大值或最小值。
3. 高阶导数高阶导数是指导数的导数,表示函数变化率的变化率。
如果函数f(x)在点x处的导数存在,那么我们可以对其求导得到f'(x)的导数,称为f(x)的二阶导数。
同理,我们可以对二阶导数求导,得到三阶导数,以此类推。
高阶导数常用于分析函数的性质和求解特定问题。
例如,如果一个函数的二阶导数大于零,那么它在该点附近是凸函数;如果一个函数的二阶导数小于零,那么它在该点附近是凹函数。
4. 高阶微分类似于高阶导数,高阶微分是指微分的微分。
如果一个函数的微分存在,那么可以对其微分再次进行微分,得到二阶微分。
同理,我们可以对二阶微分进行微分,得到三阶微分,以此类推。
高阶微分在物理学和工程学中具有重要的应用,例如在描述物体的运动过程中,高阶微分可以表示加速度和速度的变化。

3.2.1 几个常用函数的导数【学习目标】1.推导四种常有函数y c 、y x 、y x2、y 1的导数公式;x2.掌握并能运用这四个公式正确求函数的导数.【自主学习】1.用导数的定义求函数 y= f ( x) 的导数的三个步骤是什么?怎样函数 y f x 在x= x0处和过某点处的切线方程?2. 四种常有函数y c 、 y x 、y x2、y 1及y f ( x) x n(n Q*)的导数公式是什x么?怎样应用?【自主检测】(1)y x5的导数___________; y x5在x=1处的导数_______; y x5在(1,1)处的切线方程_______;(2) y x 3的导数___________; y x 3在x=1处的导数_______; y x3在 (1,1)处的切线方程 _______;(2) y x 1y x11过(1,1) 处的导数 ___________;在 x=1 处的导数 _______; y xx x x的切线方程 _______;【典型例题】例 1. 求以下函数的导数.(1)y x4x21(2) y x 4 1 x3 1 x2x 232(3) y1x2+xx2例 2.已知曲线C:y=x 3- 3x2+2x, 直线 l:y=kx,且l与C切于点(x0,y0)(x0≠ 0),求直线l 的方程及切点坐标【讲堂检测】1. 已知函数 f ( x) 在 R 上知足 y=-3x 2+3x+1,则曲线 y f ( x) 在点 (1, f (1))处的切线方程 ( )A.3 x y 4 0B.3 x y 4 0 C .3 x y 4 0D.3 x y 4 02. 若存在过点 (1,0) 的直线与曲线y x 3 和 yax 2 15 x 9 都相切, 则 a 等于__________44. 已知曲线 y= 1x 34 .33( 1)求曲线在 x=2 处的切线方程;( 2)求曲线过点( 2, 4)的切线方程 .。
刹时变化率与导数【学习目标】1.认识刹时速度、刹时变化率的观点;2.理解导数的观点,知道刹时变化率是导数,领会导数的思想及其内涵;3.会求函数在某点的导数.【自主学习】1.刹时速度、刹时变化率的观点是什么?2.导数的观点是什么?3.求函数 f (x) 在点x0处的导数f ( x0)的三个步骤是什么?4.函数 f(x) 在 x0处的导数 f ′(x 0) 与x 相关吗?5.某点导数即为函数在这点的刹时变化率,含着两层含义是什么?(1) lim y存在,则称 f(x) 在 x=x0处能否可导而且导数是什么?xx→0 (2) lim y不存在,则称 f(x) 在 x=x0处能否可导?x 0x→【自主检测】1. 质点运动规律为s t23,求质点在t 3 的刹时速度.2. 数f ( x)= x2x 在x 1 处的导数.【典型例题】例 1.求函数 y= 3x2在 x=1 处的导数 .例 2. 求函数y 11在点 x处的导数 . x2【讲堂检测】1. 已知 f(x)=ax3+3x2+2,若f ' 1 =4,则a的值等于()(A)1916(C)1310(B)33(D)332.求曲线 y=f(x)=x3在 x 1时的导数.3. 数 y=x 在x=1处的导数.【总结提高】1.局部以匀速取代变速,以均匀速度取代刹时速度,而后经过取极限,从刹时速度的近似值过渡到刹时速度的精准值,进而过渡到导数的观点.2. 理解求导数值的三个步骤:⑴求函数值的增量 : y f ( x0x) f (x0 ) ;⑵求均匀变化率:y f ( x 0x ) f ( x0 )x x并化简 ;⑶直觉lim△ y得导数 f ( x 0 ) .△ x 0△x注意:令 x=x0+ x,得f x - f x0x= x- x0,于是 f ′(x 0) = lim与定义中的 f ′(x 0) = limx- x0x 0x 0f x + x-f x→→意义同样 .x。