2017年山东科技大学考研真题712数学分析硕士研究生专业课考试试题

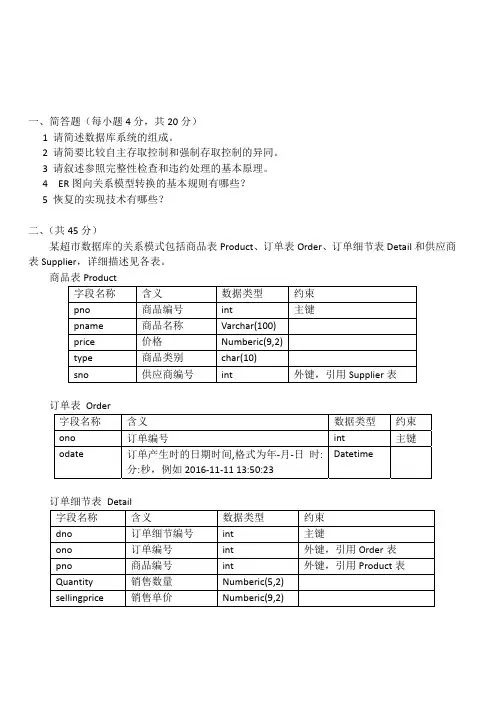
一、简答题（每小题4分，共20分）1 请简述数据库系统的组成。

2 请简要比较自主存取控制和强制存取控制的异同。

3 请叙述参照完整性检查和违约处理的基本原理。

4 ER图向关系模型转换的基本规则有哪些？5 恢复的实现技术有哪些？二、（共45分）某超市数据库的关系模式包括商品表Product、订单表Order、订单细节表Detail和供应商表Supplier，详细描述见各表。

商品表Product字段名称 含义 数据类型 约束pno 商品编号 int 主键pname 商品名称 Varchar(100)price 价格 Numberic(9,2)type 商品类别 char(10)sno 供应商编号 int 外键，引用Supplier表订单表 Order字段名称 含义 数据类型 约束ono 订单编号 int 主键odate 订单产生时的日期时间,格式为年‐月‐日 时:Datetime分:秒，例如2016‐11‐11 13:50:23订单细节表 Detail字段名称 含义 数据类型 约束dno 订单细节编号 int 主键ono 订单编号 int 外键，引用Order表pno 商品编号 int 外键，引用Product表Quantity 销售数量 Numberic(5,2)sellingprice 销售单价 Numberic(9,2)供应商表Supplier字段名称 含义 数据类型 约束sno 供应商编号 int 主键sname 供应商名称 Varchar(100)address 地址 Varchar(100)contacts 联系人 Varchar(100)zip 邮政编码 char(6)求解下列问题：1 请用关系代数表示下列查询（15分）（1）查询价格小于等于100.00的商品的供应商名称。

（2）查询在2016年没有任何商品销售的供应商名称。

（3）查询联系人为“张山”的供应商编号、名称与地址。

2 请用SQL语言表示下列查询（15分）(1)查询包含“手机”类商品的订单的编号与日期。

一、（20分）在一天中进入某超市的顾客人数ξ服从参数为λ的泊松分布，而进入超市的每一个人以概率p 购买1件商品，以概率1A p -不购买商品，假设顾客是否购买商品是相互独立的，记A A η为一天中顾客在该超市购买商品的件数。

A 1、求η的概率分布；2、求条件概率{|}p l k ξη==，其中为非负整数； ,k l 二、（20分）设随机向量(,ξηy )的联合密度函数为,01,1(,)0,Axy x x f x y ≤≤≤≤⎧=⎨⎩其它 1、求常数；A 2、求,ξη的边缘密度函数，,ξη是否独立？为什么？ 3、求概率(1/2P )η<及概率(P 1)ξη+=的值； 11(|22P ηξ)<= 4、求条件概率),(ηξ三、（20分）设二维随机变量的联合分布函数为(1)(1),0,0(,)0x y e e if x y F x y else αβ--⎧-->=⎨⎩>其中0,0αβ>> 与η1、问ξ是否独立？为什么？ 2、 求),(ηξ的联合密度函数；(2)E ξη+、()E ξη及协方差cov(,)ξηξη-+3、 求数学期望；4、 若0αβ=>，试证明ξη+与/ξη独立。

四、（14分）假设(,)X Y 服从二元正态分布221(0,2;3,4;2N -，Z X Y =+//321、求数学期望，方差；EZ DZX 与Z 2、问是否相关？是否独立？为什么？服从参数为n p }{五、（16分）1、随机变量序列n ξn ξ相互独立，的贝努利分布，其中01n p <<，证明}{n ξ服从大数定律，即对任意0ε>有11{|()|)i i P p n ξ}0,(εni =n ->→→∞∑。

2、设随机变量n ξξξ,,,21 ,(2)=0.9775,Φ相互独立，且均服从均匀分布六、（20分）1、设(0.05,0.05)U -（注：(1)0.8Φ=，试利用中心极限定理求1i i = 的近似值。

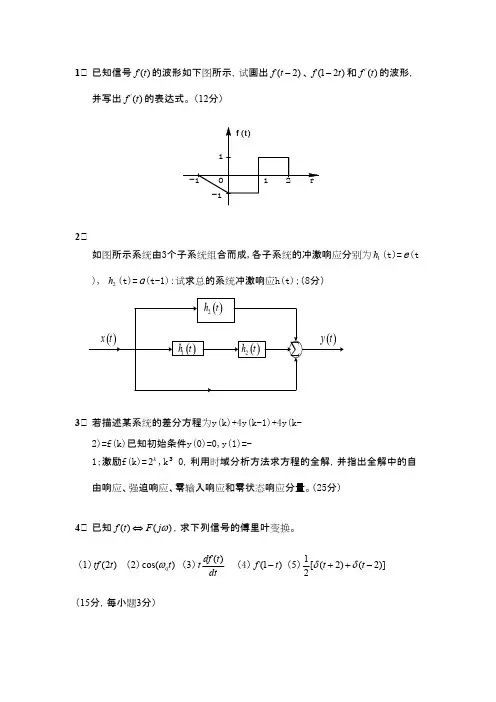
1．已知信号的波形如下图所示，试画出、和的波形，()f t (2)f t -(12)f t -'()f t 并写出的表达式。

（12分）'()f t 2．如图所示系统由3个子系统组合而成,各子系统的冲激响应分别为(t ）=(t 1h e ), (t)=(t-1)：试求总的系统冲激响应h(t)；（8分）2hd 3．若描述某系统的差分方程为y(k)+4y(k-1)+4y(k-2)=f(k)已知初始条件y(0)=0,y(1)=-1;激励f(k)=,k 0，利用时域分析方法求方程的全解，并指出全解中的自2k ³由响应、强迫响应、零输入响应和零状态响应分量。

（25分）4．已知，求下列信号的傅里叶变换。

()()f t F j ω⇔ （1） （2） （3） （4） （5）(2)tf t 0cos()t ω()df t tdt (1)f t -1[(2)(2)]2t t δδ++-（15分，每小题3分）5．已知某系统的频响特性H （jω）及激励信号的频谱F （jω）如题图所示,s （t ）（1）画出y （t ）的频谱Y （jω），并写出Y （jω）的表示式；（6分）（2）若p （t ）=cos100t ，画出y s （t ）的频谱Y s （jω）；（8分）（3）若分别对f （t ）、y （t ）和y s （t ）采样，则它们的最低抽样率与奈奎斯特间隔分别是多少。

（6分）6．求下列时间函数的拉普拉斯变换，并指出收敛域。

（8分，每小题4分）(1) (2) ()21tet ε--0(1)()k k t k δ∞=--∑7．若描述LTI 连续系统的微分方程为,激励信()()()()''''1.50.50.5r t r t r t e t ++=号为 ， ,()()e t t ε=()01r V =。

利用拉普拉斯变换求系统的零输入响应和零状态响应，并判()()'02/r V s =断自然响应和受迫响应。