平面向量的加法运算

平面向量的运算平面向量在数学中是一种重要的概念，它们被广泛应用于几何学、物理学等领域。

平面向量的运算是平面向量的基本操作，包括加法、减法、数量乘法（或标量乘法）和向量乘法（或点乘、叉乘）等。

下面将分别对这些运算进行详细介绍。

一、平面向量的加法平面向量的加法定义简单，即对应元素相加。

假设有两个平面向量A和A，它们的加法表示为：A + A = (A₁ + A₁, A₂ + A₂)其中，A₁和A₂分别为向量A的两个分量，A₁和A₂分别为向量A的两个分量。

通过按照上述规则进行相应的运算，可以得到向量的和。

二、平面向量的减法平面向量的减法类似于加法，即对应元素相减。

假设有两个平面向量A和A，它们的减法表示为：A - A = (A₁ - A₁, A₂ - A₂)其中，A₁和A₂分别为向量A的两个分量，A₁和A₂分别为向量A的两个分量。

通过按照上述规则进行相应的运算，可以得到向量的差。

三、平面向量的数量乘法平面向量的数量乘法指的是一个向量与一个标量（实数）的乘法。

假设有一个平面向量A和一个标量A，它们的数量乘法表示为：AA = (AA₁, AA₂)其中，A₁和A₂分别为向量A的两个分量。

通过按照上述规则进行相应的运算，可以得到向量与标量的乘积。

四、平面向量的向量乘法平面向量的向量乘法分为点乘和叉乘两种情况。

点乘，也称为数量积或内积，是两个向量相乘后再求和得到一个标量的运算。

假设有两个平面向量A和A，它们的点乘表示为：A·A = A₁A₁ + A₂A₂其中，A₁和A₂分别为向量A的两个分量，A₁和A₂分别为向量A的两个分量。

点乘的结果是一个标量。

叉乘，也称为向量积或外积，是两个向量相乘后得到一个新向量的运算。

假设有两个平面向量A和A，它们的叉乘表示为：A×A = (A₂A₃ - A₃A₂, A₃A₁ - A₁A₃, A₁A₂ - A₂A₁)其中，A₁、A₂和A₃分别为向量A的三个分量，A₁、A₂和A₃分别为向量A的三个分量。

平面向量的运算法则平面向量是二维的有方向和大小的量，通常用箭头表示。

在平面上，我们可以进行平面向量的加法、减法、数乘、点乘和叉乘等运算，下面将详细介绍这些运算法则。

1.平面向量的加法：设有平面向量A和B，表示为⃗A和⃗B，其加法运算为：⃗A+⃗B=⃗C，其中C是由A和B的箭头所形成的三角形的对角线的向量。

加法满足以下性质：-交换律：⃗A+⃗B=⃗B+⃗A-结合律：(⃗A+⃗B)+⃗C=⃗A+(⃗B+⃗C)2.平面向量的减法：设有平面向量A和B，表示为⃗A和⃗B，其减法运算为：⃗A-⃗⃗B=⃗C，其中C是由A的箭头指向B的箭头所形成的三角形的对角线的向量。

3.平面向量的数乘：设有平面向量A和实数k，表示为⃗A和k，其数乘运算为：k⃗A=⃗B，其中B的大小等于A的大小乘以k，方向与A相同（若k>0），或相反（若k<0）。

数乘满足以下性质：- 结合律：k(l⃗A) = (kl)⃗A-分配律：(k+l)⃗A=k⃗A+l⃗A4.平面向量的点乘（数量积）：设有平面向量A和B，表示为⃗A和⃗B，其点乘运算为：⃗A · ⃗B = ABcosθ，其中A和B的夹角θ的余弦值等于点乘结果与两个向量大小的乘积的商。

点乘满足以下性质：-交换律：⃗A·⃗B=⃗B·⃗A-结合律：(⃗A+⃗B)·⃗C=⃗A·⃗C+⃗B·⃗C-数乘结合律：(k⃗A)·⃗B=k(⃗A·⃗B)特殊情况下：-若⃗A与⃗B垂直，即⃗A·⃗B=0，则称⃗A与⃗B是正交的或垂直的。

-若⃗A和⃗B非零，且⃗A·⃗B>0，则夹角θ为锐角。

-若⃗A和⃗B非零，且⃗A·⃗B=0，则夹角θ为直角。

-若⃗A和⃗B非零，且⃗A·⃗B<0，则夹角θ为钝角。

5.平面向量的叉乘（向量积）：设有平面向量A和B，表示为⃗A和⃗B，其叉乘运算为⃗A × ⃗B = nABsinθ⃗n，其中n为垂直于A和B所在平面的单位向量，θ为A和B 的夹角。

平面向量的加法与减法性质平面向量是在平面内具有大小和方向的量，可以进行加法和减法运算。

平面向量的加法与减法性质是研究向量运算规律的重要内容。

一、平面向量的表示与加法1. 平面向量的表示平面向量通常用一个有向线段来表示，线段的长度代表向量的大小，箭头方向表示向量的方向。

用大写字母表示向量，例如 A、B、C。

2. 平面向量的加法平面向量的加法遵循平行四边形法则。

设有两个平面向量 A 和 B，A 的起点为 O，终点为 P，B 的起点为 P，终点为 Q，则向量 A+B 的起点为 O，终点为 Q，即 A+B 的表示是由 A 和 B 的起点连线和连接 A 的终点和 B 的起点的线段组成。

3. 平面向量的加法性质（1）交换律：A+B = B+A（2）结合律：(A+B)+C = A+(B+C)（3）零向量：对于任意向量 A，有 A+0 = 0+A = A，其中 0 为零向量，零向量的大小为 0，方向可以是任意方向。

二、平面向量的减法平面向量的减法运算可以转化为加法运算。

设有两个平面向量 A 和B，A 的起点为 O，终点为 P，B 的起点为 O，终点为 Q，则向量 A-B可以表示为向量 A 的起点为 O，终点为 Q，再将向量 B 倒转180°，起点为 Q，终点为 P，即 A-B = A+(-B)。

三、平面向量的性质1. 平面向量的加法性质（1）交换律：A+B = B+A（2）结合律：(A+B)+C = A+(B+C)（3）零向量：对于任意向量 A，有 A+0 = 0+A = A2. 平面向量的减法性质（1）减去一个向量等于加上该向量的相反向量：A-B = A+(-B)（2）零向量：对于任意向量 A，有 A-0 = A3. 平面向量的数乘性质平面向量的数乘运算是指将向量的大小和方向同时进行数倍的运算。

设有一个平面向量 A 和一个实数 k，则 kA 的大小为 |k|*|A|，方向与 A的方向相同（当 k>0）或相反（当 k<0）。

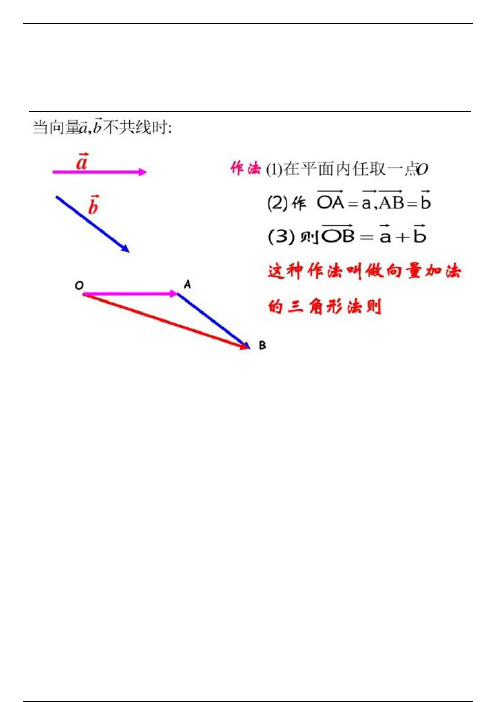
向量的加法口诀： 首尾相连，首连尾，方向指向末向量。

以第一个向量的起点为起点，以第二个向量的终点为终点的向量是两向量的和向量。

二、向量的减法两向量做减法运算，图像如下图所示：向量的减法口诀： 首首相连，尾连尾，方向指向被减向量。

以第一个向量的终点为起点，以第二个向量的终点为终点的向量是两向量的差向量。

向量的学习是高一数学必修四第二章的内容，要求同学们会向量的基本运算，其中就包括加法、减法、数乘。

要求大家能根据运算法则解决基本的向量运算，学会运用图像解决向量加减法，向量的数乘等问题。

向量的相关题目难度也不是很大，只要大家认真学习，认真做好笔记，认真做做题目，总结做题规律，那么当我们遇到类似题目时就会似曾相识，做起来也很顺手，再细心点的话，得满分也没有问题。

学习方法很多，重要的事找到适合自己的方法，当然适合自己方法就是最好的方法。

附一；三角形定则解决向量加减的方法将各个向量依次首尾顺次相接，结果为第一个向量的起点指向最后一个向量的终点。

注:两个向量相减，则表示两个向量起点的字母必须相同;差向量的终点指向被减向量的终点。

平行四边形定则解决向量加法的方法实数λ叫做向量a的系数,乘数向量λa的几何意义就是将表示向量a的有向线段伸长或压缩.当∣λ∣＞1时,表示向量a的有向线段在原方向（λ＞0）或反方向（λ＜0）上伸长为原来的λ∣倍；当∣λ∣＜1时,表示向量a的有向线段在原方向（λ＞0）或反方向（λ＜0）上缩短为原来的λ∣倍.数与向量的乘法满足下面的运算律结合律：(λa)·b=λ(a·b)=(a·λb).向量对于数的分配律（第一分配律）：(λ+μ)a=λa+μa.数对于向量的分配律（第二分配律）：λ(a+b)=λa+λb.数乘向量的消去律：① 如果实数λ≠0且λa=λb,那么a=b.② 如果a≠0且λa=μa,那么λ=μ 3、向量的的数量积定义：已知两个非零向量a,b.作OA=a,OB=b,则角AOB称作向量a和向量b的夹角,记作〈a,b〉并规定0≤〈a,b〉≤π定义：两个向量的数量积（内积、点积）是一个数量,记作a·b.若a、b不共线,则a·b=|a|·|b|·cos〈a,b〉；若a、b共线,则a·b=+-∣a∣∣b∣.向量的数量积的坐标表示：a·b=x·x'+y·y'.向量的数量积的运算律a·b=b·a（交换律）；(λa)·b=λ(a·b)(关于数乘法的结合律)；（a+b)·c=a·c+b·c（分配律）；向量的数量积的性质a·a=|a|的平方.a⊥b 〈=〉a·b=0.|a·b|≤|a|·|b|.向量的数量积与实数运算的主要不同点1、向量的数量积不满足结合律,即：(a·b)·c≠a·(b·c)；例如：(a·b)^2≠a^2·b^2.2、向量的数量积不满足消去律,即：由 a·b=a·c (a≠0),推不出 b=c.3、|a·b|≠|a|·|b|4、由 |a|=|b| ,推不出 a=b或a=-b.4、向量的向量积定义：两个向量a和b的向量积（外积、叉积）是一个向量,记作a×b.若a、b不共线,则a×b的模是：∣a×b∣=|a|·|b|·sin〈a,b〉；a×b的方向是：垂直于a和b,且a、b和a×b按这个次序构成右手系.若a、b共线,则a×b=0.向量的向量积性质：∣a×b∣是以a和b为边的平行四边形面积.。

平面向量加法
两个向量做加法运算就是向量的加法，是一种向量的运算。

向量的加法口诀：首尾相连，首连尾，方向指向末向量。

向量的减法口诀：首首相连，尾连尾，方向指向被减向量。

平面向量是在二维平面内既有方向(direction)又有大小(magnitude)的量，物理学中也称作矢量，与之相对的是只有大小、没有方向的数量（标量）。

平面向量用a,b,c上面加一个小箭头表示，也可以用表示向量的有向线段的起点和终点字母表示。

向量的加法满足平行四边形法则和三角形法则。

AB+BC=AC。

a+b=(x+x'，y+y')。

a+0=0+a=a。

向量加法的运算律：交换律：a+b=b+a；结合律：(a+b)+c=a+(b+c)。

如果a、b是互为相反的向量，那么a=-b，b=-a，a+b=0. 0的反向量为0，AB-AC=CB. 即“共同起点，指向被减”，a=(x,y) b=(x',y') 则 a-b=(x-x',y-y')。

平面向量的加减运算平面向量是表示平面上的有向线段的数学工具，常用于描述位移、速度、力等物理量。

在平面向量的运算中，加法和减法是最基本的操作。

1. 加法运算平面向量的加法运算是指将两个向量相加得到一个新的向量的操作。

设有向量A(A₁, A₂)和向量A(A₁, A₂)，则它们的和为向量A(A₁,A₂)，即：A = A + A = (A₁ + A₁, A₂ + A₂)2. 减法运算平面向量的减法运算是指将一个向量减去另一个向量得到一个新的向量的操作。

设有向量A(A₁, A₂)和向量A(A₁, A₂)，则它们的差为向量A(A₁, A₂)，即：A = A - A = (A₁ - A₁, A₂ - A₂)在进行平面向量的加减运算时，我们可以利用向量的坐标表示进行计算。

具体操作如下：1. 给出需要进行加减运算的向量A和向量A的坐标表示。

2. 将两个向量的对应坐标进行相加（或相减），得到新的坐标。

3. 根据得到的新坐标，构造新的向量A（加法运算）或向量A（减法运算）。

4. 最后，将新的向量A（加法运算）或向量A（减法运算）的坐标表示写出，即完成了平面向量的加减运算。

补充说明：1. 在计算过程中，要注意坐标的顺序，确保符号对应正确。

2. 加法运算和减法运算可以通过相互转化来进行，即：A + A = A - ( - A)3. 若有多个向量进行加减运算，可以采用逐步进行的方法，先进行第一对向量的运算，然后将得到的结果与下一个向量进行运算，依次类推。

4. 在实际问题中，应用到向量加减运算时，可以结合图像进行解释和计算，更直观地理解向量的运算规律。

通过以上步骤，我们可以完成平面向量的加减运算。

在实际应用中，平面向量的加减运算常常用于解决平面几何和物理学中的问题，如位移、速度、力的合成分解等。

总结：平面向量的加减运算是指将两个向量相加或相减得到一个新的向量。

通过计算向量的各个坐标，然后进行相应的加减操作，我们可以得到最终的结果。

平面向量的运算如何进行平面向量的加减乘除运算平面向量是描述平面上的有向线段的数学工具，具有大小和方向。

在平面向量的运算中，常见的操作包括向量的加法、减法、数量乘法和除法。

下面将详细介绍平面向量的运算方法。

一、平面向量的加法平面向量的加法是将两个向量的对应元素进行相加的运算。

设有向量A = (x1, y1)和向量B = (x2, y2)，则向量A和向量B的和为向量C = (x1 + x2, y1 + y2)。

例子：已知向量A = (1, 2)，向量B = (3, 4)，求向量A和向量B的和。

解：向量A和向量B的和为向量C = (1 + 3, 2 + 4) = (4, 6)。

二、平面向量的减法平面向量的减法是将两个向量的对应元素进行相减的运算。

设有向量A = (x1, y1)和向量B = (x2, y2)，则向量A和向量B的差为向量C = (x1 - x2, y1 - y2)。

例子：已知向量A = (1, 2)，向量B = (3, 4)，求向量A和向量B的差。

解：向量A和向量B的差为向量C = (1 - 3, 2 - 4) = (-2, -2)。

三、平面向量的数量乘法平面向量的数量乘法是指一个向量与一个实数的乘法运算。

设有向量A = (x, y)和实数k，则向量A乘以实数k的结果为向量B = (kx, ky)，即向量A的每个元素分别乘以实数k。

例子：已知向量A = (3, 4)，求向量A乘以实数2的结果。

解：向量A乘以实数2的结果为向量B = (2 × 3, 2 × 4) = (6, 8)。

四、平面向量的除法平面向量的除法并没有直接定义，因为除法运算在平面向量中没有明确的意义。

平面向量的运算主要是通过加法、减法和数量乘法来实现。

如果需要进行向量的除法运算，一般可以通过乘以倒数的方式来实现。

即将除法转化为乘法运算。

例子：已知向量A = (4, 6)，求向量A除以实数2的结果。

解：向量A除以实数2的结果可以通过将实数2转化为倒数的方式来实现，即向量A除以实数2可以表示为向量A乘以实数1/2。