化学热力学基础小结2010

热力学小结热力学是一门研究物质热运动规律的学科。

通过对热力学的学习，我了解到了热力学的基本概念、原理和应用。

下面是我的热力学学习小结。

热力学的基本概念包括热力学系统、热力学均衡态和热力学过程。

热力学系统是指我们所研究的对象，可以是封闭系统、开放系统或孤立系统。

热力学均衡态是指系统的宏观性质不随时间变化的状态。

热力学过程是指系统由一个均衡态变为另一个均衡态的过程。

热力学的原理是基于能量守恒定律和熵增原理。

能量守恒定律指出能量既不能创造也不能消失，只能由一种形式转化为另一种形式。

熵增原理是指在任何封闭系统中，熵总是增加的。

熵可以理解为系统的无序程度，熵增代表系统的无序程度增加。

热力学的应用非常广泛，涉及到能量转化、功和热的关系、热机效率等方面。

其中最常见的应用是热力学循环。

热力学循环是指系统在一系列给定步骤中的循环过程，常用于实现能量的转化和传递。

在学习热力学过程中，我发现热力学是一门抽象的学科，需要运用数学工具进行分析和计算。

例如， Gibbs 自由能和Helmholtz 自由能是热力学中常用的两个宏观性质，可以通过数学方法推导和计算出来。

此外，熵的计算也需要运用统计力学的方法。

在热力学的学习过程中，我也深刻认识到热力学是自然界中普遍存在的一种规律。

热力学的基本原理适用于各种不同的物质和系统，例如气体、液体和固体，也适用于宏观和微观尺度。

热力学原理的普适性使得热力学成为工程技术和科学研究的重要工具。

总的来说，通过对热力学的学习，我了解到了热力学的基本概念、原理和应用。

热力学的基本概念包括热力学系统、热力学均衡态和热力学过程。

热力学的原理是基于能量守恒定律和熵增原理。

热力学的应用非常广泛，涉及到能量转化、功和热的关系、热机效率等方面。

在学习热力学的过程中，我也体会到热力学是一门抽象的学科，需要运用数学工具进行分析和计算。

通过学习热力学，我对自然界的运行规律有了更深入的理解，也为将来的学习和工作打下了坚实的基础。

热⼒学⼩结化学热⼒学基础内容⼩结化学热⼒学是热⼒学原理在化学科学中的应⽤。

重点讲述了化学反应中的能量变化(即化学反应热) 和化学反应⾃发进⾏的⽅向。

1. 热⼒学第⼀定律：封闭体系：ΔU = Q + W绝热过程：Q = 0， ΔU = W循环过程： ΔU = 0，Q = – W2. 化学反应中的能量变化(化学反应热)：1) 恒容热效应数值上等于系统热⼒学能的变化：Q V = ΔU2) 恒压热效应数值上等于系统焓的变化：Q p = ΔH盖斯定律：反应热加和定律1) 在相同条件下正向反应和逆向反应的ΔH 数值相等，符号相反。

2) ⼀个反应若能分解成⼏步实现，则总反应的ΔH 等于各分步反应ΔH 值之和。

(恒温或恒压)化学反应的热效应只与物质的始态或终态有关⽽与变化途径⽆关。

3. 化学反应恒压热效应(焓变)的计算：利⽤盖斯定律或由下式计算：Δr H m ? = ∑ν产·Δf H m ?(产物) –∑ν反·Δf H m ?(反应物)4. 熵及熵变：熵的定义及其影响因素(温度、状态、分⼦⼤⼩及结构复杂性)由标准摩尔熵(S m ?)求反应的标准摩尔熵变(ΔS m ?)r S ψm = ∑n 产S ψm(产物) - ∑n 反S ψm(反应物)近似认为化学反应的焓变与熵变不随温度变化⽽变化：r H m T ≈ ?r H m ?298， ?r S m ?T ≈ ?r S m ?2985. ⾃发性判据：1) 熵判据：熵增加原理S > 0，⾃发S < 0，⾮⾃发S = 0，平衡2) ⾃由能判据：等温、等压不做⾮体积功：Δr G m(T ) < 0，⾃发Δr G m(T ) > 0，⾮⾃发Δr G m(T ) = 0，平衡6.化学反应标准⾃由能变的计算：吉布斯⽅程：r G m(T ) = r H m(298) - T r S m(298)r G m(T ) = r H m(298) - T r S m(298)r m f m f m 298.15K ()()()G n G n G ∑∑产产反＝－反当熵变和焓变符号相同，即熵变和焓变对反应⾃发性贡献互相⽭盾时，反应的⾃发性由温度决定。

热力学总结及学习感想热力学是研究能量和能量传递规律的学科，它是自然科学中的一个重要分支。

热力学的发展和运用贯穿于各个领域，涉及到物理、化学、天文学、工程学等诸多学科。

在学习热力学的过程中，我深刻认识到了热力学的基本原理和应用，并对热力学的研究方法和思维方式有了更加清晰的认识。

以下是我对热力学的总结及学习感想。

热力学的基本原理可以由三个基本定律来概括。

第一定律是能量守恒定律，它指出能量既不能自发生成，也不能自发消失，只能从一种形式转化为另一种形式。

这个定律告诉我们能量是一个可转化的物理量，并且在转化过程中总是守恒的。

第二定律是热力学中最重要的定律之一，它阐述了一个重要的物理现象——热量是从高温物体传递到低温物体的，不会反向传播。

第二定律的研究为我们理解能量转化和传递提供了重要的理论基础。

第三定律则是物质在绝对零度时熵为零的定律，它告诉我们在绝对零度时，物质的分子和原子处于最低能量状态，熵（即混乱程度）为零。

热力学的学习过程中，我通过分析热力学系统的状态变化、热力学循环和热力学平衡等基本概念，深入理解了热力学的基本原理和规律。

我学会了热力学分析中的基本方法和计算技巧，例如热力学性质的计算、热力学过程的分析等。

在解决热力学问题时，我也学会了灵活运用热力学定律和公式，结合实际问题进行推导和计算。

通过与同学的讨论和合作，我也加深了对热力学的理解，并找到了解决问题的有效方法。

在学习热力学的过程中，我深感热力学在自然科学中的重要性和广泛应用。

热力学不仅是解释和分析自然界中许多现象的重要工具，也是工程技术中的基础理论之一。

我们的生活和工作中处处都离不开热力学的应用，例如汽车引擎、空调制冷、电力发电等。

热力学的研究不仅帮助我们更好地理解自然界的奥秘，还为创新科技和解决实际问题提供了重要的理论依据。

通过学习热力学，我也培养了一些重要的学习能力和思维方式。

热力学的学习需要具备一定的数学基础和逻辑思维能力。

在解决热力学问题时，我们需要进行系统的分析和推导，运用公式和模型来描述和解释物质的能量变化和热力学性质。

《热力学》课程各章内容小结Ⅰ 温度、物态方程一．热力学系统及其平衡态热力学系统分为孤立系统、封闭系统及开放系统；系统的平衡态是在没有外界影响的条件下，系统的宏观性质不随时间变化的状态； 状态参量——描述系统平衡状态的宏观物理量：几何参量（V ）、力学参量（p ）、化学参量（1n ，2n ……）、电磁参量（E ，H ）； 对简单系统，独立变量只有两个（如p 、V ）。

二．温度与温标（一）实验表明：如果两个热力学系统同时与第三个系统处于热平衡，则这两个系统必定彼此处于热平衡——热平衡定律（热力学第零定律）。

该定律为科学地建立温度概念提供了实验基础，可证明温度是状态函数。

（二）温标是温度的数值表示法规定水的三相点温度为K 16.273，则定容气体温标为trV p pT ⨯=K 15.273，tr p 为气体在三相点时的压强； 理想气体温标为 trp p p T tr limK 15.273→⨯=，在理想气体温标确定的温度范围内，与热力学温标T 完全一致。

t （℃）＝K 15.273-T 三．物态方程均匀物质的物态方程是：0),,(=T V p f 或 ),(V p T T = 与求物态方程有关的物理量有：pT V V ⎪⎭⎫ ⎝⎛∂∂=1α——定压膨胀系数 VT p p ⎪⎭⎫ ⎝⎛∂∂=1β——定容压强系数 TT p V V ⎪⎪⎭⎫⎝⎛∂∂-=1κ——等温压缩系数因1-=⎪⎭⎫ ⎝⎛∂∂⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫⎝⎛∂∂pV T V T T p p V ，所以p T βκα= 几种物态方程：理想气体 const /=T pV 或nRT pV = 实际气体的范氏方程 ()RT b V V a p m m =-⎪⎪⎭⎫⎝⎛+2（1mol ） 简单固体 []p T T T V p T V T κα--+=)(1)0,(),(000Ⅱ 热力学第一定律一．功、热量、内能（一）准静态过程的功体积功：V p W d d -=，⎰-=BAV V V p W d表面张力的功：A W d d σ=，⎰=21d A A A W σ 功是过程量。

热学课程小结重点内容分子动理论的基本观点：1.自然界的一切宏观物体，无论是气体，液体还是固体，都是由大量分子或原子构成的。

2.分子与分子之间存在着一定的距离。

3.分子间存在相互作用力。

4.在任意时刻，某个分子位于何处，具有怎样的速度、动量、能量，都具有一定的偶然性。

但是就大量分子的整体表现来看，却呈现出一种必然的规律性，这种大量偶然事件在整体上所呈现的规律，称为统计规律。

每个分子的运动遵从力学规律，而大量分子的热运动则遵从统计规律，这就是气体动理论的基本观点 。

理想气体的微观模型：1、气体分子的大小与气体分子之间的平均距离相比要小得多，因此可以忽略不计，可将理想气体分子看作质点。

2、除分子之间的瞬间碰撞以外，可以忽略分子之间的相互作用力。

因为分子在相继两次碰撞之间作匀速直线运动。

3、分子间的相互碰撞以及分子与器壁的碰撞可以看作完全弹性碰撞。

综上所述：理想气体分子可以被看作是自由的、无规律运动者的弹性质点群。

理想气体压强的统计意义：===z y x V V VmkTV V V z yx ===222tS I P ∆∆=Kn P ε32=温度的微观意义：kT V m V m V m z y x 21212121222===K kT V m ε==23212真实气体状态方程修正的两个因素：体积修正，压强修正。

在力学中，我们把确定一个物体在空间的位置所必需的独立坐标数目定义为物体的自由度。

单原子分子：质点，自由度3 双原子分子：刚性细杆，自由度5 多原子分子：刚体，自由度6KT ik 2=ε（能量均分定理：在温度为T 的平衡态下，物质分子的每个自由度都具有相同的平均动能，其值为KT 21）麦克斯韦速率分布函数：物理意义：速率在v 附近单位速率区间内的分子数与总分子数的比。

或者说速率在v 附近单位速率区间内的分子出现的概率。

对于确定的气体，麦克斯韦速率分布函数只与温度有关。

NdvdN v f =)(dvv f N N V V )(21⎰=∆dv v f N NV V )(21⎰=∆1)(0=⎰∞dv v f三个统计速率： 1、平均速率：MRTRTV 60.182==πμ2、方均根速率MRTRTmkT V 73.133===μ3、最概然速率MRT RTmkTV P 41.122===μ单位时间内一个分子与其它分子发生碰撞的平均次数，称为平均碰撞频率，简称为碰撞频率。

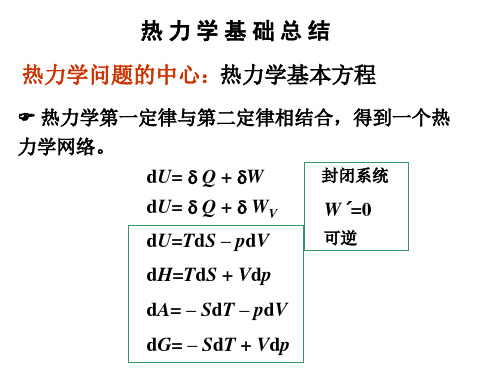
第二章热力学基础小结这一章主要讲了热力学第一定律和热力学第二定律。

一、热力学第一定律U=Q+W ∆ （封闭系统，任何过程） dU=Q W δ+δ （封闭系统微变过程）二、热力学第二定律1、 热力学第二定律的数学表达式，Clausius 不等式：QdS T δ≥B A Q S Tδ∆≥⎰ > 为不可逆＝为可逆2、熵的定义式rQ dS Tδ=BAS Br B A S AdQ dS S S S T=-=∆=⎰⎰三、状态函数及其关系式1、状态函数关系式：（定义式） H = U + pV|| ||G = A + pV+ + TS TS2、 热力学的四个基本方程:（适用条件：恒定组成，只作体积功的封闭系统） dU TdS pdV =- dH TdS Vdp =+dA SdT pdV =-- dG SdT Vdp =-+3、对应系数关系式： V p U ()()T S S ∂∂H ==∂∂ S T U A()()p V V ∂∂==-∂∂ S T H G()()V p p∂∂==∂∂ V p A G ()()S T T ∂∂==-∂∂4、Maxwell 关系式：S V T p )()V S ∂∂=-∂∂； S p T V )()P S ∂∂=∂∂； T V S p )()V T ∂∂=∂∂； T p S V)()P T∂∂=-∂∂； 四、各种判据的比较：五、各种热力学函数的计算公式： 1、体积功的计算 （1）、定义式：21V BB e V W W p dV δ==-∑⎰（2）、反抗恒定外压过程：21V e e 21V W p dV p (V V )=-=--⎰（3）、可逆过程：21V III V W = pdV -⎰（4）、理想气体恒温过程：1221V pW= nRTlnnRTln V p = （5）、有气体参加的相变过程：体系在恒温恒压下由凝聚相α转变为气相(g)β.W p(V V )pV nRT βαβ=--=-=-（6）、绝热过程： 0a Q = ,21,()a V m V m W U nC T T nC T =∆=-=∆2、热效应的计算（1）、恒容热： V Q U=∆（封闭系统，恒定W ′= 0）2211T T V V V.m T T Q U C dT n C dT =∆==⎰⎰（2）、恒压热：21p Q H H H =-=∆ （封闭系统，恒压，'0W =）2211T T p p p.m T T Q H C dT n C dT =∆==⎰⎰（3）、理想气体恒温可逆过程：12TT 21V pQ W nRTlnnRTln V p =-== （4）、绝热过程：0a Q =3、热力学能的计算（1）、封闭系统，任何过程： U=Q+W ∆ （2）、理想气体恒温过程：U ∆=0 （3）、均相物质变温过程：2211T T V V.m T T U C dT n C dT ∆==⎰⎰（4）、绝热过程：U W∆=4、焓变的计算 （1）、封闭系统：()()2211HU pV U p V pV ∆=∆+∆=∆+-（2）、理想气体恒温过程：H ∆＝0 （3）、均相物质变温过程：2211T T p p.m T T H C dT n C dT ∆==⎰⎰（4）、恒压过程：()HU p V ∆=∆+∆（5）、可逆相变过程：p m HQ n H βα∆==∆（6）、不可逆相变过程设计过程完成。