正方形内的半角模型22问

专题1.8 正方形半角模型【例题精讲】【例1】在正方形ABCD 中，点E ，F 分别在边BC ，CD 上，且45EAF CEF Ð=Ð=°．（1）将ADF D 绕着点A 顺时针旋转90°，得到ABG D （如图①)，求证：AEG AEF D @D ；（2）若直线EF 与AB ，AD 的延长线分别交于点M ，N （如图②)，求证：222EF ME NF =+．【解答】（1）证明：ADF D Q 绕着点A 顺时针旋转90°，得到ABG D ，AG AF \=，BG DF =，90GAF Ð=°，BAG DAF Ð=Ð，45EAF Ð=°Q ，904545BAE DAF BAE BAG \Ð+Ð=Ð+Ð=°-°=°，即GAE EAF Ð=Ð，\在AEG D 和AEF D 中，AG AFGAE EAF AE AE=ìïÐ=Ðíï=î，()AEG AEF SAS \D @D ；（2）证明：连接G ，如图所示：Q 四边形ABCD 是正方形，AB BC CD AD \===，90C Ð=°，45CEF Ð=°Q CE CF \=，DF DN =，BM BE =，BC CD =Q ，BE DF \=，BG DF =Q，BG DF BE BM\===，BMG\Ð=°，45Q，Ð=°EMB45EMG\Ð=°，90\=，MG同理：NF=，\=，MG NF22222EG MG ME NF ME\=+=+，Q，AEG AEFD@D\=，EG EF222\=+．EF ME NF【题组训练】1．如图，等边AEFD的顶点E，F在矩形ABCD的边BC，CD上，且45Ð=°．求证：CEF矩形ABCD是正方形．【解答】解：Q四边形ABCD是矩形，\Ð=Ð=Ð=°，B D C90Q是等边三角形，AEFDAE AF \=，60AEF AFE Ð=Ð=°，45CEF Ð=°Q ，45CFE CEF \Ð=Ð=°，180456075AFD AEB \Ð=Ð=°-°-°=°，()AEB AFD AAS \D @D ，AB AD \=，\矩形ABCD 是正方形．2．如图，在正方形ABCD 中，E 、F 分别是BC 、CD 边上的点，45EAF Ð=°．（1）如图（1），试判断EF ，BE ，DF 间的数量关系，并说明理由；（2）如图（2），若AH EF ^于点H ，试判断线段AH 与AB 的数量关系，并说明理由．【解答】（1）解：BE DF EF +=；理由如下：如图1，延长FD 到G ，使DG BE =，连接AG ，Q 在GDA D 和EBA D 中，90DG BE GDA ABE AD AB =ìïÐ=Ð=°íï=î，()GDA EBA SAS \D @D ，AG AE \=，GAD EAB Ð=Ð，故45GAF Ð=°，在GAF D 和EAF D 中，Q AG AE GAF EAF AF AF =ìïÐ=Ðíï=î，()GAF EAF SAS \D @D ，GF EF \=，即GD DF BE DF EF +=+=；（2）AH AB =，理由如下：Q 四边形ABCD 为正方形，AB AD \=，90BAD Ð=°，\把ADF D 绕点A 顺时针旋转90°得到ABQ D ，如图2，AQ AF \=，90FAQ Ð=°，90ABQ D Ð=Ð=°，而90ABC Ð=°，\点Q 在CB 的延长线上，45EAF Ð=°Q ，9045QAE EAF \Ð=°-Ð=°，EAF QAE \Ð=Ð，在AEQ D 和AEF D 中，AE AE EAF QAE AQ AF =ìïÐ=Ðíï=î，()AEQ AEF SAS \D @D ，EQ EF \=，AB EQ ^Q ，AH FE ^，AB AH \=．3．如图，在矩形ABCD 中，点E ，F 分别在BC ，CD 边上，且AE AF =，45CEF Ð=°．（1）求证：四边形ABCD 是正方形；（2）若AF =，1BE =，求四边形ABCD 的面积．【解答】（1）证明：Q 四边形ABCD 是矩形，90B D C \Ð=Ð=Ð=°，AE AF =Q ，AFE AEF \Ð=Ð，45CEF Ð=°Q ，90C Ð=°，45CFE \Ð=°，AFD AEB \Ð=Ð，()ABE ADF AAS \D @D ，AB AD \=，\矩形ABCD 是正方形．（2）解：Q 由（1）可知：AE AF ==，又1BE =，90B Ð=°，\由勾股定理得，AD ===，Q 四边形ABCD 是正方形，\217ABCD S ==正方形．4．正方形ABCD 的边长为6，E ，F 分别是AB ，BC 边上的点，且45EDF Ð=°，将DAE D绕点D 逆时针旋转90°，得到DCM D ．（1）求证：EF CF AE =+；（2）当2AE =时，求EF 的长．【解答】（1）证明：DAE D Q 逆时针旋转90°得到DCM D ，180FCM FCD DCM \Ð=Ð+Ð=°，AE CM =，F \、C 、M 三点共线，DE DM \=，90EDM Ð=°，90EDF FDM \Ð+Ð=°，45EDF Ð=°Q ，45FDM EDF \Ð=Ð=°，在DEF D 和DMF D 中，Q DE DM EDF MDF DF DF =ìïÐ=Ðíï=î，()DEF DMF SAS \D @D ，EF MF \=，EF CF AE \=+；（2）解：设EF MF x ==，2AE CM ==Q ，且6BC =，628BM BC CM \=+=+=，8BF BM MF BM EF x \=-=-=-，624EB AB AE =-=-=Q ，在Rt EBF D 中，由勾股定理得222EB BF EF +=，即2224(8)x x +-=，解得：5x =，则5EF =．5．（1）如图①，点E 、F 分别在正方形ABCD 的边AB 、BC 上，45EDF Ð=°，连接EF ，求证：EF AE FC =+．（2）如图②，点E ，F 在正方形ABCD 的对角线AC 上，45EDF Ð=°，猜想EF 、AE 、FC 的数量关系，并说明理由．【解答】证明：（1）Q 四边形ABCD 是正方形，AB BC CD AD \===，90B C ADC DAB Ð=Ð=Ð=Ð=°，如图①：延长BA ，使AM CF =，连接MD ，在AMD D 和CFD D 中，AM CF MAD C AD CD =ìïÐ=Ðíï=î，()AMD CFD SAS \D @D，MDA CDF \Ð=Ð，MD DF =，45EDF Ð=°Q ，45ADE FDC \Ð+Ð=°，45ADM ADE MDE \Ð+Ð=°=Ð，MDE EDF \Ð=Ð，在EDF D 和EDM D 中，MD DF MDE FDE DE DE =ìïÐ=Ðíï=î，()EDF EDM SAS \D @D ，EF EM \=，EM AM AE AE CF =+=+Q ，EF AE CF \=+；（2）222EF AE CF =+，理由如下：如图②，将CDF D 绕点D 顺时针旋转90°，可得ADN D ，由旋转的性质可得DN DF =，AN CF =，45DAN DCF Ð=Ð=°，CDF ADN Ð=Ð，90CAN CAD DAN \Ð=Ð+Ð=°，222EN AE AN \=+，45EDF Ð=°Q ，45CDF ADE \Ð+Ð=°，45ADE ADN NDE EDF \Ð+Ð=°=Ð=Ð，在EDF D 和EDN D中，FDE NDE DE DE ïÐ=Ðíï=î，()EDF EDN SAS \D @D ，EF EN \=，222EF AE CF \=+．6．（1）如图1，点E 、F 分别在正方形ABCD 的边BC 、CD 上，45EAF Ð=°，求证：EF BE FD =+；（2）如图2，四边形ABCD 中，90BAD й°，AB AD =，180B D Ð+Ð=°，点E 、F 分别在边BC 、CD 上，则当EAF Ð与BAD Ð满足什么关系时，仍有EF BE FD =+，说明理由．【解答】证明：（1）如图1：把ABE D 绕点A 逆时针旋转90°至ADG D ，则ADG ABE D @D ，AG AE \=，DAG BAE Ð=Ð，DG BE =，又45EAF Ð=°Q ，即45DAF BEA EAF Ð+Ð=Ð=°，GAF FAE \Ð=Ð，在GAF D 和EAF D中，GAF FAE AF AF ïÐ=Ðíï=î，()GAF EAF SAS \D @D ．GF EF \=．又DG BE =Q ，GF BE DF \=+，BE DF EF \+=；（2）当2BAD EAF Ð=Ð时，仍有EF BE FD =+，理由如下：如图2，延长CB 至M ，使BM DF =，连接AM ，180ABC D Ð+Ð=°Q ，180ABC ABM Ð+Ð=°，D ABM \Ð=Ð，在ABM D 和ADF D 中，AB AD ABM D BM DF =ìïÐ=Ðíï=î，()ABM ADF SAS \D @D AF AM \=，DAF BAM Ð=Ð，2BAD EAF Ð=ÐQ ，DAF BAE EAF \Ð+Ð=Ð，EAB BAM EAM EAF \Ð+Ð=Ð=Ð，在FAE D 和MAE D 中，AE AE FAE MAE AF AM =ìïÐ=Ðíï=î，()FAE MAE SAS \D @D ，EF EM BE BM BE DF \==+=+，即EF BE DF =+．7．（类比学习，从图1中找方法在图2中运用）（1）如图1，在正方形ABCD （四条边都相等，每个内角都是90)°中，E 是AB 上一点，G 是AD 上一点，F 是AD 延长线上一点，且45GCE Ð=°，BE DF =．求证：GE BE GD =+．（2）如图2，已知：AC 平分BAD Ð，CE AB ^，CD CB =，180B D Ð+Ð=°．求证：AE AD BE =+．【解答】证明：（1）在正方形ABCD 中，BC CD =，在BCE D 和DCF D 中，90BC CD B CDF DF BE =ìïÐ=Ð=°íï=î，()BCE DCF SAS \D @D ，CE CF \=，BCE DCF Ð=Ð，45GCE Ð=°Q ，904545GCF GCD DCF GCD BCE \Ð=Ð+Ð=Ð+Ð=°-°=°，GCF GCE \Ð=Ð，在GCE D 和GCF D 中，CE CF GCF GCE CG CG =ìïÐ=Ðíï=î，()GCE GCF SAS \D @D ，EG GF \=，GF GD DF =+Q ，GE BE GD \=+；（2）延长AB 到F 使BF AD =，180ABC CBF \Ð+Ð=°，180ABC D Ð+Ð=°Q ，CBF D \Ð=Ð，CD CB =Q ，()CDA CBF SAS \D @D ，DAC F \Ð=Ð，AC Q 平分BAD Ð，DAC CAE \Ð=Ð，CAE F \Ð=Ð，AC FC \=，CE AB ^Q ，AE EF \=，AE AD BE \=+．8．（1）如图1的正方形ABCD 中，点E ，F 分别在边BC ，CD 上，45EAF Ð=°，延长CD 到点G ，使DG BE =，连接EF ，AG ．求证：EF FG =；（2）如图2，等腰Rt ABC D 中，90BAC Ð=°，AB AC =，点M ，N 在边BC 上，且45MAN Ð=°．若1BM =，3CN =，求MN 的长．【解答】（1）证明：在正方形ABCD 中，ABE ADG Ð=Ð，AD AB =，在ABE D 和ADG D 中，AD AB ABE ADG DG BE =ìïÐ=Ðíï=î，()ABE ADG SAS \D @D ，BAE DAG \Ð=Ð，AE AG =，90EAG \Ð=°，在FAE D 和GAF D 中，45AE AG EAF FAG AF AF =ìïÐ=Ð=°íï=î，()FAE FAG SAS \D @D ，EF FG \=；（2）解：如图，过点C 作CE BC ^，垂足为点C ，截取CE ，使CE BM =．连接AE 、EN ．AB AC =Q ，90BAC Ð=°，45B ACB \Ð=Ð=°．CE BC ^Q ，45ACE B \Ð=Ð=°．在ABM D 和ACE D 中，AB AC B ACE BM CE =ìïÐ=Ðíï=î，()ABM ACE SAS \D @D ．AM AE \=，BAM CAE Ð=Ð．90BAC Ð=°Q ，45MAN Ð=°，45BAM CAN \Ð+Ð=°．于是，由BAM CAE Ð=Ð，得45MAN EAN Ð=Ð=°．在MAN D 和EAN D 中，AM AE MAN EAN AN AN =ìïÐ=Ðíï=î，()MAN EAN SAS \D @D ．MN EN \=．在Rt ENC D 中，由勾股定理，得222EN EC NC =+．222MN BM NC \=+．1BM =Q ，3CN =，22213MN \=+，MN \=9．如图，四边形ABCD 是正方形，点E 是BC 边上的动点（不与点B 、C 重合），将射线AE 绕点A 按逆时针方向旋转45°后交CD 边于点F ，AE 、AF 分别交BD 于G 、H 两点．（1）当55BEA Ð=°时，求HAD Ð的度数；（2）设BEA a Ð=，试用含a 的代数式表示DFA Ð的大小；（3）点E 运动的过程中，试探究BEA Ð与FEA Ð有怎样的数量关系，并说明理由．【解答】解：（1）Q四边形ABCD是正方形，\Ð=Ð=°，90EBA BAD\Ð=°-Ð=°-°=°，EAB AEB90905535\Ð=Ð-Ð-Ð=°-°-°=°；HAD BAD EAF EAB90453510（2）Q四边形ABCD是正方形，\Ð=Ð=Ð=°，90EBA BAD ADF\Ð=°-Ð=°-，EAB AEB a9090\Ð=Ð-Ð-Ð=°-°-°-=-°，DAF BAD EAF EAB a a9045(90)45\Ð=°-Ð=°--°=°-；DFA DAF a a9090(45)135（3）BEA FEAÐ=Ð，理由如下：延长CB至I，使BI DF=，连接AI．Q四边形ABCD是正方形，AD AB\=，90Ð=Ð=°，ADF ABC\Ð=°，ABI90又BI DFQ，=\D@D，DAF BAI SAS()\=，DAF BAIÐ=Ð，AF AIEAI BAI BAE DAF BAE EAF\Ð=Ð+Ð=Ð+Ð=°=Ð，45又AED的公共边，Q是EAID与EAF()EAI EAF SAS \D @D ，BEA FEA \Ð=Ð．10．如图，在正方形ABCD 中，E 是AB 边上一点，F 是AD 延长线上一点，BE DF =．（1）求证：CE CF =；（2）若点G 在AD 边上，且45GCE Ð=°，3BE =，5DG =，求GE 的长．【解答】（1）证明：Q 四边形ABCD 是正方形，BC DC \=，90B FDC Ð=Ð=°，在EBC D 和FDC D 中，DF EB FDC B CB DC =ìïÐ=Ðíï=î，()CBE CDF SAS \D @D ，CE CF \=；（2）解：由（1）得：CBE CDF D @D ，BCE DCF \Ð=Ð，BCE ECD DCF ECD \Ð+Ð=Ð+Ð，即90ECF BCD Ð=Ð=°，又45GCE Ð=°Q ，45GCF GCE \Ð=Ð=°，Q 在ECG FCG D @D 中，CE CF GCE GCF GC GC =ìïÐ=Ðíï=î，()ECG FCG SAS \D @D，358GE GF DG DF DG BE \==+=+=+=．11．如图，Rt CEF D 中，90C Ð=°，CEF Ð，CFE Ð外角平分线交于点A ，过点A 分别作直线CE ，CF 的垂线，B ，D 为垂足．（1）求证：四边形ABCD 是正方形．（2）已知AB 的长为6，求(6)(6)BE DF ++的值．（3）借助于上面问题的解题思路，解决下列问题：若三角形PQR 中，45QPR Ð=°，一条高是PH ，长度为6，2QH =，则HR =　3或12　．【解答】（1）证明：作AG EF ^于G ，如图1所示：则90AGE AGF Ð=Ð=°，AB CE ^Q ，AD CF ^，90B D C \Ð=Ð=°=Ð，\四边形ABCD 是矩形，CEF ÐQ ，CFE Ð外角平分线交于点A ，AB AG \=，AD AG =，AB AD \=，\四边形ABCD 是正方形；（2）解：Q 四边形ABCD 是正方形，6BC CD \==，在Rt ABE D 和Rt AGE D 中，AE AE AB AD =ìí=î，Rt ABE Rt AGE(HL)\D @D ，BE BG \=，同理：Rt ADF Rt AGF(HL)D @D ，DF GF \=，BE DF GE GF EF \+=+=，设BE x =，DF y =，则6CE BC BE x =-=-，6CF CD DF y =-=-，EF x y =+，在Rt CEF D 中，由勾股定理得：222(6)(6)()x y x y -+-=+，整理得：6()36xy x y ++=，(6)(6)(6)(6)6()36363672BE DF x y xy x y \++=++=+++=+=；（3）解：①PQR D 是锐角三角形时，如图2所示：把PQH D 沿PQ 翻折得PQD D ，把PRH D 沿PR 翻折得PRM D ，延长DQ 、MR 交于点G ，由（1）（2）得：四边形PMGD 是正方形，MR DQ QR +=，MR HR =，2DQ HQ ==，6MG DG MP PH \====，4GQ \=，设MR HR a ==，则6GR a =-，2QR a =+，在Rt GQR D 中，由勾股定理得：222(6)4(2)a a -+=+，解得：3a =，即3HR =；②当PQR D 是钝角三角形时，过P 作PT PR ^交RQ 延长线于T ，如图3所示：则904545TPQ Ð=°-°=°，由①得：3TH =，PT \===设HR x =，PR y =，则3TR x =+，PTR D Q 的面积11(3)622x =+´=´，\62x =+，225(62)y x \=+①，在Rt PRH D 中，由勾股定理得：2226y x =+②，由①②得：2(12)0x -=，12x \=，即12HR =；综上所述，HR 为3或12，故答案为：3或12．12．（1）如图1，在正方形ABCD 中，E 是AB 上一点，G 是AD 上一点，45ECG Ð=°，那么EG 与图中两条线段的和相等？证明你的结论．（2）请用（1）中所积累的经验和知识完成此题，如图2，在四边形ABCG 中，//()AG BC BC AG >，90B Ð=°，12AB BC ==，E 是AB 上一点，且45ECG Ð=°，4BE =，求EG 的长？【解答】解：（1）EG BE DG=+．如图1，延长AD至F，使DF BE=，连接CF，Q四边形ABCD为正方形，Ð=Ð=Ð=°，BC DCABC ADC BCD\=，90Q，Ð=-Ð180CDF ADC\Ð=°，CDF90\Ð=Ð，ABC CDFQ，=BE DF\D@D，()EBC FDC SAS=，\Ð=Ð，EC FCBCE DCFQ，Ð=°45ECGBCE GCD BCD ECG\Ð+Ð=Ð-Ð=°-°=°，904545\Ð+=Ð=°，45GCD DCF FCG\Ð=Ð，ECG FCG=Q，GC GC\D@D，()ECG FCG SASEG GF \=，GF GD DF GD BE =+=+Q ，EG GD BE \=+．（2）如图2，过点C 作CD AG ^，交AG 的延长线于D ．//AG BC Q ，180A B \Ð+Ð=°，90B Ð=°Q ，18090A B \Ð=°-Ð=°，90CDA Ð=°Q ，AB BC =，\四边形ABCD 是正方形，12AB BC ==Q ，12CD AD \==，4BE =Q ，8AE AB BE \=-=，设EG x =，由（1）知EG BE GD =+，4GD x \=-，12(4)16AG AD GD x x \=-=--=-，在Rt AEG D 中：222GE AG AE =+，222(16)8x x \=-+，解得10x =，10EG \=．13．如图，在正方形ABCD 中，点E 、F 分别为边BC 、CD 上两点，45EAF Ð=°，过点A 作GAB FAD Ð=Ð，且点G 为边CB 延长线上一点．①GAB FAD D @D 吗？说明理由．②若线段4DF =，8BE =，求线段EF 的长度．③若4DF =，8CF =．求线段EF 的长度．【解答】解：①全等．证明：Q 四边形ABCD 为正方形AB AD \=，ABG D Ð=Ð，在ABG D 和ADF D 中，GAB FAD Ð=Ð，AB AD =，ABG D Ð=ÐGAB FAD \D @D ．②解：90BAD Ð=°Q ，45EAF Ð=°45DAF BAE \Ð+Ð=°GAB FADD @D Q GAB FAD \Ð=Ð，AG AF=45GAB BAE \Ð+Ð=°45GAE \Ð=°GAE EAF\Ð=Ð在GAE D 和FAE D 中AG AF =Q ，GAE EAF Ð=Ð，AE AE=()GAE FAE SAS \D @D EF GE \=．GAB FADD @D Q GB DF\=8412EF GE GB BE FD BE \==+=+=+=．③设EF x =，则4BE GE BG x =-=-．EC BC BE =-Q ，12(4)16EC x x \=--=-．在Rt EFC D 中，依据勾股定理可知：222EF FC EC =+，即222(16)8x x -+=，解得：10x =．10EF \=．14．如图，Rt CEF D 中，90C Ð=°，CEF Ð，CFE Ð外角平分线交于点A ，过点A 分别作直线CE ，CF 的垂线，B ，D 为垂足．（1）EAF Ð=　45　°（直接写出结果不写解答过程）；（2）①求证：四边形ABCD 是正方形．②若3BE EC ==，求DF 的长．（3）如图（2），在PQR D 中，45QPR Ð=°，高5PH =，2QH =，则HR 的长度是 （直接写出结果不写解答过程）．【解答】解：（1）90C Ð=°Q ，90CFE CEF \Ð+Ð=°，36090270DFE BEF \Ð+Ð=°-°=°，AF Q 平分DFE Ð，AE 平分BEF Ð，12AFE DFE \Ð=Ð，12AEF BEF Ð=Ð，11()27013522AEF AFE DFE BEF \Ð+Ð=Ð+Ð=´°=°，18045EAF AEF AFE \Ð=°-Ð-Ð=°，故答案为：45；（2）①作AG EF ^于G ，如图1所示：则90AGE AGF Ð=Ð=°，AB CE ^Q ，AD CF ^，90B D C \Ð=Ð=°=Ð，\四边形ABCD 是矩形，CEF ÐQ ，CFE Ð外角平分线交于点A ，AB AG \=，AD AG =，AB AD \=，\四边形ABCD 是正方形；②设DF x =，3BE EC ==Q ，6BC \=，由①得四边形ABCD 是正方形，6BC CD \==，在Rt ABE D 与Rt AGE D 中，AB AG AE AE =ìí=î，Rt ABE Rt AGE(HL)\D @D ，3BE EG \==，同理，GF DF x ==，在Rt CEF D 中，222EC FC EF +=，即2223(6)(3)x x +-=+，解得：2x =，DF \的长为2；（3）解：如图2所示：把PQH D 沿PQ 翻折得PQD D ，把PRH D 沿PR 翻折得PRM D ，延长DQ 、MR 交于点G ，由（1）（2）得：四边形PMGD 是正方形，MR DQ QR +=，MR HR =，2DQ HQ ==，5MG DG MP PH \====，3GQ \=，设MR HR a ==，则5GR a =-，2QR a =+，在Rt GQR D 中，由勾股定理得：222(5)3(2)a a -+=+，解得：157a =，即157HR =；故答案为：157．16．如图，已知正方形ABCD 的边长为6，E ，F 分别是AB 、BC 边上的点，且45EDF Ð=°，将DAE D 绕点D 逆时针旋转90°，得到DCM D ．（1）求证：EF MF=（2）若2AE =，求FC 的长．【解答】解：（1）DAE D Q 逆时针旋转90°得到DCM D ，180FCM FCD DCM \Ð=Ð+Ð=°，F \、C 、M 三点共线，DE DM \=，90EDM Ð=°．90EDF FDM \Ð+Ð=°，45EDF Ð=°Q ，45FDM EDF \Ð=Ð=°，()DEF DMF SAS \D @D ，EF MF \=．（2）设EF MF x ==，2AE CM ==Q ，且6BC =，628BM BC CM \=+=+=，8BF BM MF BM EF x \=-=-=-，624EB AB AE =-=-=Q ．在Rt EBF D 中，由勾股定理得222EB BF EF +=．即2224(8)x x +-=，\解得：5x =，即5FM =．523FC FM CM \=-=-=．17．设E 、F 分别在正方形ABCD 的边BC ，CD 上滑动保持且45EAF Ð=°，AP EF ^于点P ．（1）求证：AP AB =；（2）若5AB =，求ECF D 的周长．【解答】证明：（1）延长CB 到F ¢，使BF DF ¢=，在正方形ABCD 中，AB AD =，90ABC D Ð=Ð=°，18090ABF ABC D \Т=°-Ð=°=Ð，()ABF ADF SAS \D ¢@D ，AF AF \¢=，12Ð=Ð，13239045EAF EAF EAF \Т=Ð+Ð=Ð+Ð=°-Ð=°=Ð，又EA EA =Q ，()EAF EAF SAS \D ¢@D ，EF EF \¢=，AEF AEF S S ¢D D =，而1122EF AB EF AP ¢=g g ，AB AP \=．解：（2）CEF C EC CF EFD =++EC CF EF =++¢EC BE CF BF =+++¢BC CF DF=++210BC CD AB =+==．18．如图，在正方形ABCD 中，E 是AB 上一点，F 是AD 延长线上一点，且DF BE =．（1）求证：CE CF =；（2）若点G 在AD 上，且45GCE Ð=°，则GE BE GD =+成立吗？为什么？【解答】（1）证明：在正方形ABCD 中，Q BC DC B CDF BE DF =ìïÐ=Ðíï=î，()CBE CDF SAS \D @D ．CE CF \=．（2）解：GE BE GD =+成立．理由是：Q 由（1）得：CBE CDF D @D ，BCE DCF \Ð=Ð，BCE ECD DCF ECD \Ð+Ð=Ð+Ð，即90ECF BCD Ð=Ð=°，又45GCE Ð=°Q ，45GCF GCE \Ð=Ð=°．Q CE CF GCE GCF GC GC =ìïÐ=Ðíï=î，()ECG FCG SAS \D @D ．GE GF \=．GE DF GD BE GD \=+=+．19．正方形ABCD 的边长为3，E 、F 分别是AB 、BC 边上的点，且45EDF Ð=°．将DAE D 绕点D 逆时针旋转90°，得到DCM D ．（1）求证：EF FM =；（2）当1AE =时，求EF 的长．【解答】解：（1）证明：DAE D Q 逆时针旋转90°得到DCM D ，180FCM FCD DCM \Ð=Ð+Ð=°，F \、C 、M三点共线，DE DM \=，90EDM Ð=°，90EDF FDM \Ð+Ð=°，45EDF Ð=°Q ，45FDM EDF \Ð=Ð=°，在DEF D 和DMF D 中，DE DM EDF MDF DF DF =ìïÐ=Ðíï=î，()DEF DMF SAS \D @D ，EF MF \=；（2）设EF MF x ==，1AE CM ==Q ，且3BC =，314BM BC CM \=+=+=，4BF BM MF BM EF x \=-=-=-，312EB AB AE =-=-=Q ，在Rt EBF D 中，由勾股定理得222EB BF EF +=，即2222(4)x x +-=，解得：52x =，则52EF =．。

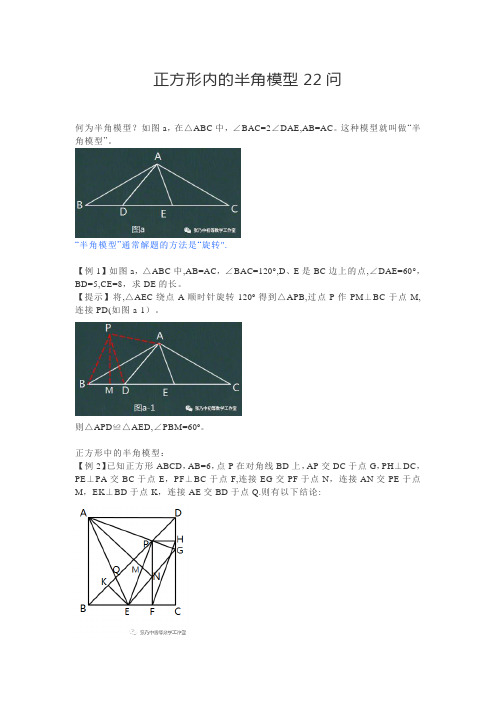
正方形内的半角模型22问何为半角模型？如图a，在△ABC中，∠BAC=2∠DAE,AB=AC。

这种模型就叫做“半角模型”。

“半角模型”通常解题的方法是“旋转".【例1】如图a，△ABC中,AB=AC，∠BAC=120°,D、E是BC边上的点,∠DAE=60°，BD=5,CE=8，求DE的长。

【提示】将,△AEC绕点A顺时针旋转120º得到△APB,过点P作PM⊥BC于点M,连接PD(如图a-1）。

则△APD≌△AED,∠PBM=60º。

正方形中的半角模型：【例2】已知正方形ABCD，AB=6，点P在对角线BD上，AP交DC于点G，PH⊥DC，PE⊥PA交BC于点E，PF⊥BC于点F,连接EG交PF于点N，连接AN交PE于点M，EK⊥BD于点K，连接AE交BD于点Q.则有以下结论:（1）△PAE是等腰直角三角形；（2）EF=FC（四边形EFHP为平行四边形）；(3）PB-PD=√2BE；（4）EG=EB+DG；（5）BC+BE=√2BP;（6)GA平分∠DGE;（7)A到EG的距离为定值；（8）△EFN的周长为定值;（9）FH=AP;（10）∠BAE=∠BPE；（11）NE=NG=NP(∠NEP=∠NPE，∠NPG=∠NGP）；（12）∠KEQ=∠PEN;（13）∠APB=∠AEG；（14)∠DGE=2∠AQD;（15）PQ²=BQ²+PD²；(16）AB=√2PK（PK=3√2）;（17）若BE=2,则PF=4且DG=GC；（18）若∠EPF=22.5º，则PF=PK;（19）若△PEC是等边三角形，则PE=6√3—6（PF=9-3√3，PD=3√6-3√2);(20)S△ABE=6,则S△ECG=6；（21)若AN⊥EG，则PD=6√2—6；（22）若AN⊥EG，则NA—NE=√2NP。

【解析】（1)延长FP（如图1—1），则PIDH为正方形，∠EPF=∠PAI，∴△EPF≌△PAI,∴PA=PE，又PE⊥AP,∴△PAE为等腰直角三角形；（2）EF=IP=ID=FC，PH∥EF，故四边形EFHP为平行四边形;（3）PB-PD=√2BF—√2PH=√2(BF—PH）=√2(BF-EF）=√2BE；（4）将△ADG绕点A顺时针旋转90º得到△ABJ（如图1-2).则AJ=AG，∠GAE=∠JAE=45º，AE=AE，∴△GAE≌△JAE，JE=EG，JE=JB+BE,JB=DG，∴EG=EB+DG；（5)∵BP=BD-PD=√2BC-√2FC，∴√2BP=2BC-2FC=BC+（BC—FC-EF）=BC+BE；（6)由(4），∠AJB=∠AGE=∠AGD，故GA平分∠DGE；(7)由（4），∠AEB=∠AEG=∠AGD，故A到EG的距离=AB=6，为定值; （8）C△ECG=EC+CG+EG=EC+CG+GD+BE=BC+CD=12，∵EF=FC，FN∥CG，∴N为EG中点，C△EFN=C△ECG÷2=6，为定值；（9）连接PC（如图1-3）,根据对称性，PA=PC，四边形FCHP为矩形，∴PC=FH，∴PA=FH；（10）∵∠BAE+∠DAG=45º,∠BPE+∠EPF=45º，∠EPF=∠DAG（参照（1）的证明），∴∠BAE=∠BPE；（11)由(8）知，点N为EG中点，△EPG为直角三角形，∴NE=NG=NP(∠NEP=∠NPE，∠NPG=∠NGP）；（12)∠KEQ=∠AEB-45º=90º—∠BAE -45º=45º—∠BAE=∠DAG；∠PEN=∠EPN=∠DAG，∴∠KEQ=∠PEN；（13）∠APB=∠BPC=45º+∠FPC=45º+∠EPN=45º+∠PEN=∠AEG；（14）∠AQD=45º+∠BAE=45º+45º—∠DAG=90º-∠DAG=∠AGD，∴2∠AQD=2∠AGD=∠DGE；（15）将△ABQ绕点A逆时针旋转90º得到△ADR，连接RP(如图1—4）。

半角模型
1、产生条件：共顶点、等线段，一个小角等于大角的一半，对角互补的四边形。

2、常见形式：图形中，往往出现90°套45°的情况，或者120°套60°的情况，还有2α套α的情况。

求证的结论一般是“a+b=c 或者a -b=c ”。

3、解题方法: 通过辅助线“截长补短”，构造全等三角形，转移边角。

旋转移位造全等，翻折分割构全等。

4、经典题型：
4.1、正方形半角模型：90°→ 45°
例1、如图，正方形ABCD 中，∠EAF=45°。

求证： （1）EF=BE+DF ． （2）∠EFC 周长 = 2AB （3）EA 平分∠BEF
变式训练：
如图，正方形ABCD 中，∠EAF=45°。

求证：EF=DF - BE
B
B
4.2、等腰直角三角形半角模型：90°→ 45°
例2、如图，等腰直角三角形中∠BAC=90°，∠EAF=45°，求证：BE 、EF 、CF 的数量关系。

变式训练：
如图，等腰直角三角形中∠BAC=90°，∠EAF=45°，求证：BE 2 + CF 2 = EF 2。

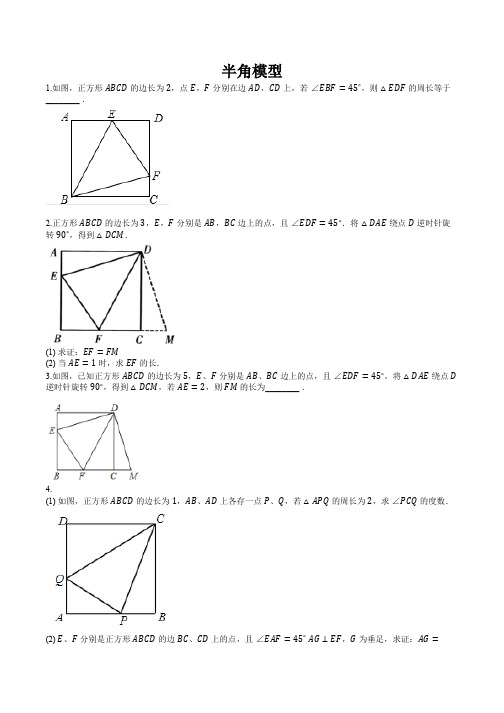
半角模型1.如图，正方形ABCD的边长为2，点E，F分别在边AD，CD上，若∠EBF=45∘，则△EDF的周长等于________ ．2.正方形ABCD的边长为3，E，F分别是AB，BC边上的点，且∠EDF=45∘．将△DAE绕点D逆时针旋转90∘，得到△DCM．(1) 求证：EF=FM(2) 当AE=1时，求EF的长．3.如图，已知正方形ABCD的边长为5，E、F分别是AB、BC边上的点，且∠EDF=45∘，将△DAE绕点D 逆时针旋转90∘，得到△DCM，若AE=2，则FM的长为________ ．4.(1) 如图，正方形ABCD的边长为1，AB、AD上各存一点P、Q，若△APQ的周长为2，求∠PCQ的度数．(2) E、F分别是正方形ABCD的边BC、CD上的点，且∠EAF=45∘AG⊥EF，G为垂足，求证：AG=AB．5.如图，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE．(1) 求证：CE=CF；(2) 若点G在AD上，且∠GCE=45∘，则GE=BE+GD成立吗？为什么？6.如图，已知正方形ABCD边长为1，∠EAF=45∘，AE=AF，则有下列结论：①∠1=∠2=22.5∘②点C到EF的距离是√2−1③△ECF的周长为2④BE+DF>EF其中正确的结论是 ________．（写出所有正确结论的序号）7.如图，已知正方形ABCD的边长为8 cm，点E、F分别在边BC、CD上，∠EAF=45∘．当EF=8 cm 时，△AEF的面积是________ cm2；当EF=7 cm时，△EFC的面积是________ cm2．8.如图，正方形ABCD的边长为6，点E、F分别在AB、AD上，若CE=3√5，且∠ECF=45∘，则CF的长为 ()A．2√10 B．3√5 C．53√10D．103√59.(1) 如图，正方形ABCD的边长为1，AB、AD上各存一点P、Q，若△APQ的周长为2，求∠PCQ的度数．(2) E、F分别是正方形ABCD的边BC、CD上的点，且∠EAF=45∘，AG⊥EF，G为垂足，求证：AG= AB．10.如图，在正方形ABCD中，E是边AB上一点，点F是AD延长线上一点，且DF=BE．(1) 求证：CE=CF；(2) 若G是AD上一点，且∠GCE=45∘①证明：GE=BE+GD；②设BE=4，GE=10，求△CEG的面积．11.如图1，在正方形ABCD内作∠EAF=45∘，AE交BC于点E，AF交CD于点F，连接EF，过点A作AH⊥EF，垂足为H．图1图2图3(1) 如图2，将△ADF绕点A顺时针旋转90∘得到△ABG．①求证：△AGE≅△AFE；②若BE=2，DF=3，求AH的长．(2) 如图3，连接BD交AE于点M，交AF于点N．请探究并猜想：线段BM，MN，ND之间有什么数量关系？并说明理由．12.如图（1），已知正方形ABCD中，E，F分别是BC，CD边上的点，且∠EAF=45∘，判断线段BE，EF，FD之间的数量关系，并说明理由．小明同学的想法是：已知条件比较分散，可以通过旋转变换将分散的已知条件集中在一起，于是他将△DAF绕点A顺时针旋转90∘，得到△BAH，然后通过证明三角形全等可得出结论．请你参考小明同学的思路，解决下列问题：(1) 图1中线段BE，EF，FD之间的数量关系是________；(2) 如图2，已知正方形ABCD边长为5，E，F分别是BC，CD边上的点，且∠EAF=45∘，AG⊥EF于点G，则AG的长为________，△EFC的周长为________；(3) 如图3，已知△AEF中，EAF=45∘，AG⊥EF于点G，且EG=2，GF=3，则△AEF的面积为________．13.如图，在正方形ABCD中，AB=1，E，F分别是边BC，CD上的点，连接EF、AE、AF，过A作AH⊥EF于点H．若EF=BE+DF．那么下列结论：①AE平分∠BEF②FH=FD③∠EAF=45∘④S△EAF=S△ABE+S△ADF；⑤△CEF的周长为2其中正确结论的是 ________ ．14.如图，在Rt△ABC中，AB=AC，D、E是斜边BC上两点，且∠DAE=45∘，将△ADC绕点A顺时针旋转90∘后，得到△AFB，连接EF，下列结论：（1）△AED≅△AEF（2）△ABE≅△ACD（3）BE+DC=DE（4）BE2+DC2=DE2其中正确结论有 () 个A．1B．2C．3D．415.如图，在△ABC中，∠BAC=90∘，AB=AC，点D、E均在边BC上，且∠DAE=45∘，猜想BD、DE、EC应满足的等量关系，并写出推理过程．16.如图，在△ABC中，AB=AC=2√2，∠BAC=90∘，点D、E都在边BC上，∠DAE=45∘，若BD= 2CE，则DE的长是 ()A．1B．3−√52C．3√5−52D．3√5−517.四边形ABCD被对角线BD分为等腰直角三角形ABD和直角三角形CBD，其中∠A和∠C都是直角，另一条对角线AC的长度为2，求四边形ABCD的面积．18.在等腰直角△ABC中，∠ACB=90∘，AC=BC．M是AB的中点，点P从B出发向点C运动，MQ⊥MP交AC于点Q．试说明△MPQ的形状和面积将如何变化．19.如图所示，△ABD是等边三角形，在△ABC中，BC=a，CA=b．问：当∠ACB为何值时，C、D两点间的距离最大？最大值是多少？20.如图所示，点D为∠ABC的平分线BD上一点，点E、F分别为∠ABC两边上的动点，且∠ABC+∠EDF=180∘．连接DE、DF，判断在E、F运动过程中，DE、DF的数量关系并证明．21.如图，P是正方形ABCD内一点，∠APB=135∘，BP=1，AP=√7，求PC的值．()A．√5B．3C．2√2D．222.点P为等腰直角三角形ABC内一点，∠ACB=90∘，PB=1，PC=2，PA=3，求∠BPC的度数．23.如图．设P是等边△ABC内的一点，且PA:PB:PC=3:4:5，求∠APB的度数．24.如图，△ABC是边长为3的等边三角形，△BDC是等腰三角形，且∠BDC=120∘，以D为顶点作一个60∘角，使其两边分别交AB于点M，交AC于点N，连接MN，则△AMN的周长为 ()A．9B．8C．7D．625.△ABC是边长为1的等边三角形，△BDC是顶角为120∘的等腰三角形，∠MDN=60∘，求△AMN 的周长．26.D为等边△ABC外一点，且BD=CD，∠BDC=120∘，点M，N分别在AB，AC上，若BM+CN= MN，(1) ∠MDN= ________度；(2) 作出三角形△DMN的高DH，并证明：DH=BD；(3) 在第（2）的基础上，求证：MD平分∠BDH．27.如图，△ABC等边三角形，△BDC是顶角∠BDC=120∘的等腰三角形，以D为顶点作一个60∘角，角的两边分别交AB、AC于M、N，连接MN，若SΔBMD +SΔCND=10，则SΔDMN= ________ ．28.如图，在四边形ABCD中，∠B+∠ADC=180∘，AB=AD，E、F分别是边BC、CD延长线上的点，且∠EAF=12∠BAD，求证：EF=BE−FD．29.如图，已知等边△ABC外有一点H，连接CH、BH，BH=CH且∠BHC=120∘，在AB上取点E、在AC上取点F，若∠EHF=60∘，设EH、FH分别交BC于P、Q两点，试证明以下结论：=2BC(1) CΔAEF(2) AF=2BP，AE=2CQ半角模型1.【答案】4【解析】∵四边形ABCD为正方形∴AB=BC，∠BAE=∠C=90∘∴把△ABE绕点B顺时针旋转90∘可得到△BCG，如图∴BG=AE，CG=AE，∠GBE=90∘，∠BAE=∠C=90∘∴点G在DC的延长线上∵∠EBF=45∘∴∠FBG=∠EBG−∠EBF=45∘∴∠FBG=∠FBE在△FBG和△EBF中，{BF=BF∠FBG=∠FBEBG=BE∴△FBG≌△FBE(SAS)∴FG=EF∵FG=FC+CG=CF+AE∴EF=CF+AE∴△DEF的周长=DF+DE+CF+AE=CD+AD=2+2=42.(1)【答案】证明见解析【解析】∵△DAE逆时针旋转90∘得到△DCM∴DE=DM，∠EDM=90∘∴∠EDF+∠FDM=90∘∵∠EDF=45∘∴∠FDM=∠EDF=45∘∵DF=DF∴△DEF≅△DMF∴EF=MF(2)【答案】52【解析】设EF=x∵AE=CM=1∴BF=BM−MF=BM−EF=4−x∵EB=2由勾股定理得：EB2+BF2=EF2即22+(4−x)2=x2，解得：x=523.【答案】297【解析】∵△DAE逆时针旋转90∘得到△DCM∴∠FCM=∠FCD+∠DCM=180∘∴F、C、M三点共线∴DE=DM，∠EDM=90∘∴∠EDF+∠FDM=90∘∵∠EDF=45∘∴∠FDM=∠EDF=45∘∵DF=DF∴△DEF≅△DMF∴EF=MF设EF=MF=x∵AE=CM=2，且BC=5∴BM=BC+CM=7∴BF=BM−MF=BM−EF=7−x∵EB=AB−AE=3在Rt△EBF中，由勾股定理得：EB2+BF2=EF2即32+(7−x)2=x2，解得：x=297∴FM=29 74.(1)【答案】45∘【解析】如图所示，延长AB至点E，使得BE=DQ，连接CE，证△CDQ≅△CBE，再证△CQP≅△CEP(2)【答案】证明见解析【解析】如图所示，延长FB至点Q，使得BQ=DE，连接AQ先证△ADE≅△ABQ，再证△AQF≅△AEF，利用面积法可得AB=AG5.(1)【答案】证明见解析【解析】∵四边形ABCD为正方形∴BC=CD，∠B=∠ADC=90∘在△BEC和△DFC中，{BC=CD∠B=∠CDF BE=DF∴△CBE≅△CDF(SAS)∴CE=CF(2)【答案】成立，理由见解析【解析】∵由（1）得△CBE≅△CDF∴∠BCE=∠DCF∴∠BCE+∠ECD=∠DCF+∠ECD，即∠ECF=∠BCD=90∘∵∠GCE=45∘∴∠GCF=∠GCE=45∘∵CE=CF，∠GCE=∠GCF，GC=GC∴△ECG≅△FCG(SAS)∴GE=GF∴GE=DF+GD=BE+GD6.【答案】①②③【解析】∵四边形ABCD为正方形∴AB=AD，∠BAD=∠B=∠D=90∘在Rt△ABE和Rt△ADF中，{AE=AFAB=AD∴Rt△ABE≅Rt△ADF∴∠1=∠2∵∠EAF=45∘∴∠1=∠2=∠22.5∘，故①正确；连接EF、AC，它们相交于点H，如图所示：∵Rt△ABE≅Rt△ADF∴BE=DF∵BC=DC∴CE=CF∵AE=AF∴AC垂直平分EF，AH平分∠EAF∴EB=EH，FD=FH∴BE+DF=EH+HF=EF，故④错误；∴C△ECF=CE+CF+EF=CE+BE+CF+DF=CB+CD=2，故③正确；设BE=x，则EF=2x，CE=1−x∵△CEF为等腰直角三角形∴EF=√2CE，即2x=√2(1−x)，解得：x=√2−1∴EF=2(√2−1)∴CH=12EF=√2−1，故②正确；故答案为①②③7.【答案】32；8【解析】如图所示，延长CB到G，使得BG=DF，连接AG∵四边形ABCD是正方形∴AB=AD，∠D=∠ABG=90∘∵BG=DF∴△ABG≅△ADF∴AG=AF，∠GAB=∠FAD∵∠EAF=45∘∴∠FAD+∠BAE=45∘∴∠GAE=∠FAE=45∘∵AE=AE∴△GAE≅△FAE∴EF=EG=8∴S△AEF=S△AEG=12×8×8=32当EF=7时，由上述结论可知：S△EFC=S正方形ABCD −2S△AEF=8×8−2×12×7×8=64−56=88.【答案】A【解析】如图，延长FD到G，使DG=BE，连接CG、EF∵四边形ABCD为正方形在△BCE与△DCG中，{CB=CD∠CBE=∠CDGBE=DG∴△BCE≅△DCG ( SAS )∴ CG=CE，∠DCG=∠BCE∴∠GCF=45∘在△GCF与△ECF中，{GC=EC∠GCF=∠ECFCF=CF∴△GCF≅△ECF ( SAS )∴ GF=EF∵ CE=3√5，CB=6∴ BE=√CE2−CB2=√(3√5)2−62=3∴ AE=3设AF=x，则DF=6−x，GF=3+(6−x)=9−x∴ EF=√AE2+x2=√9+x2∴ (9−x)2=9+x2∴ x=4，即AF=4∴ GF=5∴ DF=2∴ CF=√CD2+DF2=√62+22=2√10故选 A9.(1)【答案】45∘【解析】如图所示，将Rt△CDQ绕点C逆时针旋转90∘易证P、B、E三点共线∵AQ+QD+AP+PB=AD+AB=1+1=2∴AQ+AP+PQ=AQ+QD+AP+PB，即PQ=QD+PB=PE∵PC=PC,CQ=CE,PQ=PE∴△PQC≅△PEC(SSS)∴∠PCQ=∠PCE=45∘(2)【答案】证明见解析【解析】把△ADE绕点A顺时针旋转90∘，得△ABQ∵FA=FA,∠FAQ=∠FAE=45°,AQ=AE,∴△AFQ≅△AFE(SAS)∴AB=AG10.(1)【答案】证明见解析【解析】在正方形ABCD中，∵{BC=CD∠B=∠CDFBE=DF∴△CBE≅△CDF (SAS)∴CE=CF(2)【答案】①证明见解析；②60【解析】①∵由 (1) 得：△CBE≅△CDF∴∠BCE=∠DCF∴∠BCE+∠ECD=∠DCF+∠ECD，即∠ECF=∠BCD=90∘∵∠GCE=45∘∴∠GCF=∠GCE=45∘∵{CE=CF∠GCE=∠GCFGC=GC∴△ECG≅△FCG (SAS)∴GE=GF∴GE=DF+GD=BE+GD ②由①得：GE=BE+GD∵BE=4，GE=10∴GD=6设正方形的边长为x，则AG=x−6，AE=x−4由勾股定理得：(x−6)2+(x−4)2=102解得：x1=12，x2=−2（舍去）∴正方形的边长为12∴AG=6，AE=8∴△GAE的面积为24，△CDG的面积为36，△CBE的面积为24，正方形ABCD的面积为144∴△CGE的面积为6011.(1)【答案】①见解析；②6【解析】①由旋转的性质可知：AF=AG，∠DAF=∠BAG∵四边形ABCD为正方形∴∠BAD=90∘∵∠EAF=45∘∴∠BAE+∠DAF=45∘∴∠BAG+∠BAE=45∘∴∠GAE=∠FAE在△GAE和△FAE中，{AG=AF∠GAE=∠FAEAE=AE，∴△GAE≅△FAE②∵△GAE≅△FAE，AB⊥GE，AH⊥EF∴AB=AH，GE=EF=5设正方形的边长为x，则EC=x−2，FC=x−3在Rt△EFC中，由勾股定理得：EF2=FC2+EC2即(x−2)2+(x−3)2=25，解得：x=6∴AB=6∴AH=6(2)【答案】见解析【解析】如图所示，将△ABM逆时针旋转90∘得△ADM′∵四边形ABCD为正方形∴∠ABD=∠ADB=45∘由旋转的性质可知：∠ABM=∠ADM′=45∘，BM=DM′∴∠NDM′=90∘∴NM′2=ND2+DM′2∠EAM′=90∘，∠EAF=45∘∴∠EAF=∠FAM′=45∘在△AMN和△AM′N中，{AM=AM′∠MAN=∠M′ANAN=AN∴△AMN≅△AM′N∴MN=NM′∵BM=DM′∴MN2=ND2+BM2 12.(1)【答案】EF=BE+FD【解析】△AHB≅△AFD，△AEH≅△AEF(2)【答案】5；10【解析】∵△FAE≅△HAE，AG，AB分别是△FAE与△HAE的高∴AG=AB=5∵Rt△AEG≅Rt△ABE∴EG=BE同理得：GF=DF∴△EFC的周长为BC+CD=10(3)【答案】15【解析】将△AEF置于图2中∵EG=2，GF=3∴BE=2，DF=3，EF=5设AB=x，则CE=x−2，CF=x−3在△CEF中，根据勾股定理，解得x=−1（舍去），x=6∴AG=AB=6∴S△AEF=12EF⋅AG=1513.【答案】①②③④⑤【解析】如图，延长CB到G点，使BG=DF，连接AG，则EF=EG在△ADF和△ABG中，∵AD=AB，∠D=∠ABG，DF=BG∴△ADF≅△ABG (SAS)∴∠GAB=∠FAD，AG=AF在△AEF和△AEG中，∵AG=AF，EF=EG，AE=AE∴△AEF≅△AEG (SSS)∴∠GEA=∠FEA，即AE平分∠BEF故①正确；∵∠ABE=∠AHE=90∘，∠AEB=∠AEH，AE=AE∴△ABE≅△AHE (AAS)∴BE=EH∴FH=BG=FD故②正确；∠EAF=∠GAE=∠GAB+∠BAE=∠DAF+∠BAE∴∠EAF=12∠BAD=12×90∘=45∘故③正确；∵△ABE≅△AHE (AAS)，△AHF≅△ADF (HL)∴S△EAF=S△ABE+S△ADF故④正确；∵△CEF的周长=CE+CF+EF=CE+CF+BE+DF=1+1=2故⑤正确；故正确的有：①②③④⑤14.【答案】B【解析】∵△ADC绕点A顺时针旋转90∘得△AFB∴△ADC≅△AFB，∠FAD=90∘∴AD=AF∵∠DAE=45∘∴∠FAE=90∘−∠DAE=45∘∴∠DAE=∠FAE，AE为△AED和△AEF的公共边∴△AED≅△AEF∴ED=FE在Rt△ABC中，∠ABC+∠ACB=90∘∵∠ACB=∠ABF∴∠ABC+∠ABF=90∘，即∠FBE=90∘∴在Rt△FBE中，BE2+BF2=FE2∴BE+DC=DE故正确的有（1）（4）故选 B15.【答案】BD2+EC2=DE2，证明见解析【解析】如图所示，作AF⊥AE，使AF=AE∵∠DAE=∠DAF=45∘∵AD=AD∴△ADE≅△ADF∴DF=DE∵∠BAF=∠CAE=45∘−∠BAD，AB=AC∴△ABF≅△ACE∴BF=CE，∠ABF=∠ACE∴∠FBD=∠ABF+∠ABC=∠ACE+∠ABC=90∘∴BD2+EC2=BD2+BF2=DF2=DE216.【答案】D【解析】∵ΔABC中，AB=AC=2√2，∠BAC=90∘∴∠ABC=∠C=45∘由勾股定理得：BC=√AB2+AC2=4把ΔAEC绕A点旋转到ΔAFB，使AB和AC重合，连接DF则AF=AE，∠FBA=∠C=45∘，∠BAF=∠CAE∵∠DAE=45∘∴∠FAD=∠FAB+∠BAD=∠CAE+∠BAD=∠BAC−∠DAE=90∘−45∘=45∘∴∠FAD=∠DAE=45∘在ΔFAD和ΔEAD中，{AD=AD∠FAD=∠EADAF=AE∴ΔFAD≅ΔEAD(SAS)∴DF=DE，BF=EC设EC=x，则BF=x，BD=2x，DF=DE=√5x∵BC=4∴2x+√5x+x=4，解得：x=3−√5∴DE=√5x=√5(3−√5)=3√5−5故选 D17.【答案】2【解析】“对角互补”+“邻边相等”的四边形，已知对角线的长度并不能直接求面积．利用旋转可将四边形变形成我们熟悉的三角形如图：延长CD到点E，使DE=BC，连接AE易证：△ABC ≅△ADE所以S△ABC=S△ADE，AC=AE，∠BAC=∠DAE所以△ACE为等腰直角三角形，S四边形ABCD =S△ACE=12×22=218.【答案】略【解析】如图，连接CM易证△MQC ≅△MPB，所以MQ=MP 所以△MPQ为等腰直角三角形，形状不变△MPQ的面积与边MP的长度有关当点P从点B到BC中点时，面积由大变小当点P是BC中点时，三角形的面积最小当点P继续向点C运动时，面积由小变大19.【答案】∠ACB=120∘时，C、D两点间的距离最大，为a+b【解析】如图，以CD为边作等边三角形DCC′，所以CD=CC′易证△DBC ≅△DAC′，所以AC′=BC=a在△ACC′中，AC+AC′>CC′当C，A，C′三点共线时，AC+AC′=CC′=a+b所以CD的最大值为a+b此时∠ACB=∠ACD+∠BCD=∠ACD+∠AC′D=180∘−60∘=120∘20.【答案】DE=DF【解析】如图，过点D分别作BA和BC的垂线段，垂足分别为H和Q易证：△DHE ≅△DQF，所以DE=DF21.【答案】B【解析】如图，把△PBC绕点B逆时针旋转90∘得到△ABP′（点C的对应点C′与点A重合），所以，AP′=PC，BP′=BP=1，所以，△PBP′是等腰直角三角形，所以，∠P′PB=45∘，PP′=√BP2+BP′2=√12+12=√2，∵∠APB=135∘，∴∠APP′=∠APB−∠P′PB=135∘−45∘=90∘，在Rt△APP′中，AP′=√PP′2+AP2=√(√2)2+(√7)2=3，∴PC=AP′=3.22.【答案】∠BPC=135∘．【解析】如图，把△ACP绕点C逆时针旋转90∘得到△BCD，连接DP，∵△ACP绕点C逆时针旋转90∘得到△BCD，∴CP=CD=2，∠DCP=90∘，DB=PA=3，∴△CPD为等腰直角三角形，∴PD=√2PC=2√2，∠CPD=45∘，在△PDB中，PB=1，PD=2√2，DB=3，而12+(2√2)2=32，∴PB2+PD2=BD2，∴△PBD为直角三角形，∴∠DPB=90∘，∴∠BPC=45∘+90∘=135∘．23.【答案】∠APB=150∘．【解析】将ΔPBC绕点B逆时针旋转60∘得ΔDAB，则BP=BD，∠DBP=60∘，∴ΔDBP为等边三角形，∠DPB=60∘，设AD=PC=5k，DP=BP=4k，∵AP2+DP2=(3k)2+(4k)2=25k2=AD2，∴ΔADP是直角三角形，∠APD=90∘，∴∠APB=∠APD+∠DPB=150∘．24.【答案】D【解析】∵△BDC是等腰三角形，且∠BDC=120∘∴∠DBC=∠BCD=30∘∵△ABC是边长为3的等边三角形∴∠ABC=∠BAC=∠BCA=60∘∴∠DBA=∠DCA=90∘延长AB至F，使BF=CN，连接DF∴ BF =CN ，DB =DC∴ Rt △BDF ≌Rt △CDN∴ ∠BDF =∠CDN ，DF =DN∵ ∠MDN =60∘∴ ∠BDM +∠CDN =60∘∴ ∠BDM +∠BDF =60∘ ∴ ∠FDM =∠MDN =60∘∴ △DMN ≌△DMF∴ MN =MF ∴ △AMN 的周长 =AM +AN +MN =AM +MB +BF +AN =AB +AC =6故选 D25.【答案】1【解析】如图所示，延长 BD 交 AC 于 P ，延长 CD 交 AB 于 Q ，在 PC 上截取 KP =QM ，交 AC 于 P ，连接 DK∵ △BDC 是等腰三角形，且 ∠BDC =120∘ ∴ BD =CD ，∠DBC =∠DCB =30∘，∠BDQ =∠CDP =60∘ ∵ △ABC 等边三角形∴ ∠ABC =∠ACB =60∘ ∴ ∠MBD =∠PCD =30∘，CQ ⊥AB ，BP ⊥AC ∴ AQ =BQ =12AB =12，AP =PC =12AC =12在 △BDQ 和 △CDP 中，{∠QBD =∠PCDBD =CD∠BDQ =∠CDP∴ △BDQ ≌△CDP(ASA)∴ BQ =PC ，QD =PD∵ CQ ⊥AB ，BP ⊥AC∴ ∠MQD =∠DPK =90∘在 △MDQ 与 △PDK 中，{∠MQD=∠DPKQM=PK∴△MDQ≌△PDK(SAS)∴∠QDM=∠PDK，DM=DK∵∠BDQ=60∘，∠MDN=60∘∴∠QDM+∠PDN=60∘∴∠PDK+∠PDN=60∘，即∠KDN=60∘在△MDN与△KDN中，{DM=DK∠MDN=∠KDN=60∘DN=DN∴△MDN≌△KDN(SAS)∴MN=KN=NP+PK∴△AMN的周长=AM+AN+MN=AM+AN+NP+PK=AM+AN+NP+QM=AQ+AP=126.(1)【答案】60∘【解析】如图所示，将△BDM顺时针旋转120∘得到△CDE则DM=DE,∠BDM=∠CDE,BM=CE∴EN=CE+CN=BM+CN=MN∵BM+CN=MN在 △DMN 和 △DEN 中，{MN =EN DM =DE DN =DN∴△DMN ≅△DEN(SSS)∴∠MDN =∠EDN(2)【答案】证明见解析【解析】如图所示，延长 AC 至 E ，使 CE =BM ，连接 DE∵△ABC 是等边三角形∴∠ABC =∠ACB =60∘∵BD =CD ，∠BDC =120∘∴∠CBD =∠BCD =30∘∴∠ABD =∠ACD =90∘∴∠ABD =∠ECD =90∘∴△BDM ≅△CDE (SAS)∴DM =DE∵NE =NC +CE =NC +BM =MN ，DN =DN∴△DMN ≅△DEN (SSS)∴∠DNM =∠DNE∵DH ⊥MN ，DC ⊥AC∴DH =DC∵BD =DC∴DH =BD(3)【答案】证明见解析【解析】∵∠ABD =90∘，DH ⊥MN ，DH =BD ，DM =DM∴△BDM ≅△HDM∴∠BDM =∠HDM∴ MD 平分 ∠BDH27.【答案】10【解析】如图所示，延长 AB 至 K ，使 ∠KDN =∠BDC =120∘易证：△KDB≌△NDC，△DKM≌△DNM则S△DMN=S△BMD+S△CND=1028.【答案】证明见解析【解析】如图所示，在BE上截取BG，使BG=DF，连接AG∵∠B+∠ADC=180∘，∠ADF+∠ADC=180∘∴∠B=∠ADF 在△ABG和△ADF中，{AB=AD∠B=∠ADFBG=DF∴△ABG≅△ADF(SAS)∴∠BAG=∠DAF，AG=AF∴∠BAG+∠EAD=∠DAF+∠EAD=∠EAF=12∠BAD∴∠GAE=∠EAF 在△AEG和△AEF中，{AG=AF∠GAE=∠EAFAE=AE∴△AEG≅△AEF(SAS)∴EG=EF∵EG=BE−BG ∴EF=BE−FD29.(1)【答案】证明见解析【解析】如图所示，延长EB至M，使BM=CF，连接HM易证：△HCF≌△HBM(SAS)，△HFE≌△HME(SAS)∴EF=BE+CF∴C△AEF=2BC(2)【答案】证明见解析【解析】如图所示，过E作ES//AC交BC于S，交HF于T由HF平分∠EFC得：△EFT为等腰三角形∴EF=ET∵△BES为等边三角形∴ST=CF，AE=CS∴△QCF≌△QST(ASA)∴QC=QS∴AE=2CQ同理可证：AF=2BP。

半角模型例题已知，正方形ABCD 中，∠EAF 两边分别交线段BC 、DC 于点E 、F ，且∠EAF ﹦45° 结论1：BE ﹢DF ﹦EF结论2：S △ABE ﹢S △ADF ﹦S △AEF 结论3：AH ﹦AD结论4：△CEF 的周长﹦2倍的正方形边长﹦2AB 结论5：当BE ﹦DF 时，△CEF 的面积最小 结论6：BM 2﹢DN 2﹦MN 2结论7：三角形相似，可由三角形相似的传递性得到 结论8：EA 、FA 是△CEF 的外角平分线 结论9：四点共圆 结论10：△ANE 和△AMF 是等腰直角三角形（可通过共圆得到） 结论11：MN ﹦√22EF （可由相似得到）结论12：S △AEF ﹦2S △AMN （可由相似的性质得到） 结论5的证明：设正方形ABCD 的边长为1 则S △AEF ﹦1﹣S 1﹣S 2﹣S 3﹦1﹣12x ﹣12y ﹣12(1﹣x)(1﹣y) ﹦12﹣12xy所以当x ﹦y 时，△AEF 的面积最小结论6的证明：将△ADN 顺时针旋转90°使AD 与AB 重合 ∴DN ﹦BN ′易证△AMN ≌△AMN ′ ∴MN ﹦MN ′在Rt △BMN ′中，由勾股定理可得： BM 2﹢BN ′2﹦MN ′2 即BM 2﹢DN 2﹦MN 2结论7的所有相似三角形：△AMN ∽△DFN△AMN ∽△BME△AMN ∽△BAN△AMN ∽△DMA△AMN ∽△AFE结论8的证明：因为△AMN ∽△AFE ∴∠3＝∠2因为△AMN ∽△BAN ∴∠3＝∠4 ∴∠2＝∠4 因为AB ∥CD ∴∠1＝∠4 ∴∠1＝∠2结论9的证明：因为∠EAN ﹦∠EBN ＝45°∴A 、B 、E 、N 四点共圆（辅圆定理：共边同侧等顶角）同理可证C 、E 、N 、F 四点共圆 A 、M 、F 、D 四点共圆 C 、E 、M 、F 四点共圆**必会结论-------- 图形研究正方形半角模型已知：正方形ABCD ，E 、F 分别在边BC 、CD 上，且︒=∠45EAF ，AE 、AF 分别交BD 于H 、G ，连EF .一、全等关系（1）求证：①EF BE DF =+；②DG 2﹢BH 2﹦HG 2；③AE 平分BEF ∠，AF 平分DFE ∠. 二、相似关系（2）求证：①DG CE 2=；②BH CF 2=；③HG EF 2=. （3）求证：④DH BG AB ⋅=2；⑤HG BG AG ⋅=2；⑥21=⋅CF DF CE BE . 三、垂直关系（4）求证：①EG AG ⊥；②FH AH ⊥；③BEAB HCF =∠tan . （5)、和差关系求证：①BE DG BG 2=-；②DH DF AD 2=+； ③||2||DG BH DF BE -=-.例1、在正方形ABCD 中，已知∠MAN ﹦45°，若M 、N 分别在边CB 、DC 的延长线上移动，①.试探究线段MN 、BM 、DN 之间的数量关系. ②.求证：AB=AH.例2、在四边形ABCD 中，∠B+∠D ﹦180°，AB=AD ，若E 、F 分别在边BC 、CD 上，且满足EF=BE +DF. 求证：∠EAF ＝12∠BAD例3、在△ABC 中，AB=AC ，∠BAC=2∠DAE=120°，若BD=5，CE=8，求DE 的长。

几何模型系列：正方形中的半角模型20个常用结论，欢迎交流半角模型是全等三角形中一种常见的几何模型，正方形中的半角模型是最常见的一种，做过不
少相关题型，总感觉题型之间有某种相似之处，也拜读过很多的大神的文章，最后决定搜集整
理，好好琢磨一番，最后整理出正方形中的半角模型的20个常用结论，希望与学生与教育同行
一起交流。

半角模型在中考几何中也是经常遇见，本篇文章就不再介绍其具体的应用，只分析
正方形中的半角模型，不分析其他图形的半角模型。

一、什么叫半角模型
定义：
我们习惯把过等腰三角形顶角的顶点引两条射线，使两条射线的夹角为等腰三角形顶角的一半
这样的模型称为半角模型。

1、常见的图形
正方形，正三角形，等腰直角三角形等。

2、解题思路
①将半角两边的三角形通过旋转到一边合并形成新的三角形；
②证明与半角形成的三角形全等；
③通过全等的性质得出线段之间的数量关系，从而解决问题。

二、半角模型有哪些常见结论，我们该如何证明。

正方形半角模型的15个结论
正方形半角模型是指在正方形的四个顶点处各分出一个角度为45度的扇形，然后将这四个扇形组合在一起，形成一个半角模型。

以下是正方形半角模型的15个结论：
1. 正方形半角模型的中心是正方形的中心。

2. 正方形半角模型的四条弧线互相垂直。

3. 正方形半角模型的四个扇形完全相等。

4. 正方形半角模型的圆心角度为180度。

5. 正方形半角模型的周长等于正方形周长的一半。

6. 正方形半角模型的半径等于正方形边长的一半。

7. 正方形半角模型的直径等于正方形的对角线长度。

8. 正方形半角模型的面积等于正方形面积的一半。

9. 正方形半角模型的外接圆半径等于正方形的边长。

10. 正方形半角模型的内切圆半径等于正方形的边长的平方根减去正方形边长的一半。

11. 正方形半角模型的内部四边形的面积等于正方形面积的一半减去正方形边长的平方。

12. 正方形半角模型的内部四边形是菱形。

13. 正方形半角模型的对角线分别是内部四边形的对角线。

14. 正方形半角模型的对角线相交于圆心。

15. 正方形半角模型的内部四边形的对角线长度等于正方形边长的平方根减去正方形边长的一半。

半角模型例题已知,正方形ABCD 中,∠EAF 两边分别交线段BC 、DC 于点E 、F,且∠EAF ﹦45° 结论1:BE ﹢DF ﹦EF结论2:S △ABE ﹢S △ADF ﹦S △AEF 结论3:AH ﹦AD结论4:△CEF 得周长﹦2倍得正方形边长﹦2AB 结论5:当BE ﹦DF 时,△CEF 得面积最小 结论6:BM 2﹢DN 2﹦MN 2结论7:三角形相似,可由三角形相似得传递性得到 结论8:EA 、FA 就是△CEF 得外角平分线 结论9:四点共圆结论10:△ANE 与△AMF 就是等腰直角三角形(可通过共圆得到) 结论11:MN ﹦EF(可由相似得到)结论12:S △AEF ﹦2S △AMN(可由相似得性质得到) 结论5得证明:设正方形ABCD 得边长为1 则S △AEF ﹦1﹣S 1﹣S 2﹣S 3﹦1﹣x ﹣y ﹣(1﹣x)(1﹣y) ﹦﹣xy所以当x ﹦y 时,△AEF 得面积最小结论6得证明:将△ADN 顺时针旋转90°使AD 与AB 重合 ∴DN ﹦BN ′易证△AMN ≌△AMN ′ ∴MN ﹦MN ′在Rt △BMN ′中,由勾股定理可得: BM 2﹢BN ′2﹦MN ′2 即BM 2﹢DN 2﹦MN 2结论7得所有相似三角形:△AMN ∽△DFN△AMN ∽△BME△AMN ∽△BAN△AMN ∽△DMA△AMN ∽△AFE结论8得证明:因为△AMN ∽△AFE ∴∠3＝∠2因为△AMN ∽△BAN ∴∠3＝∠4 ∴∠2＝∠4 因为AB ∥CD ∴∠1＝∠4 ∴∠1＝∠2结论9得证明:因为∠EAN ﹦∠EBN ＝45° ∴A 、B 、E 、N 四点共圆(辅圆定理:共边同侧等顶角)同理可证C 、E 、N 、F 四点共圆 A 、M 、F 、D 四点共圆 C 、E 、M 、F 四点共圆**必会结论-------- 图形研究正方形半角模型已知:正方形ABCD ,E 、F 分别在边BC 、CD 上,且︒=∠45EAF ,AE 、AF 分别交BD 于H 、G ,连EF 、一、全等关系(1)求证:①EF BE DF =+;②DG 2﹢BH 2﹦HG 2;③AE 平分BEF ∠,AF 平分DFE ∠、 二、相似关系(2)求证:①DG CE 2=;②BH CF 2=;③HG EF 2=、 (3)求证:④DH BG AB ⋅=2;⑤HG BG AG ⋅=2;⑥21=⋅CF DF CE BE 、 三、垂直关系(4)求证:①EG AG ⊥;②FH AH ⊥;③BEAB HCF =∠tan 、 (5)、与差关系求证:①BE DG BG 2=-;②DH DF AD 2=+; ③||2||DG BH DF BE -=-、例1、在正方形ABCD 中,已知∠MAN ﹦45°,若M 、N 分别在边CB 、DC 得延长线上移动,①、试探究线段MN 、BM 、DN 之间得数量关系、 ②、求证:AB=AH 、例2、在四边形ABCD 中,∠B+∠D ﹦180°,AB=AD,若E 、F 分别在边BC 、CD 上,且满足EF=BE +DF 、 求证:∠EAF ＝∠BAD例3、在△ABC 中,AB=AC,∠BAC=2∠DAE=120°,若BD=5,CE=8,求DE 得长。