竞赛作业2(静力学)
- 格式:doc
- 大小:195.00 KB
- 文档页数:2

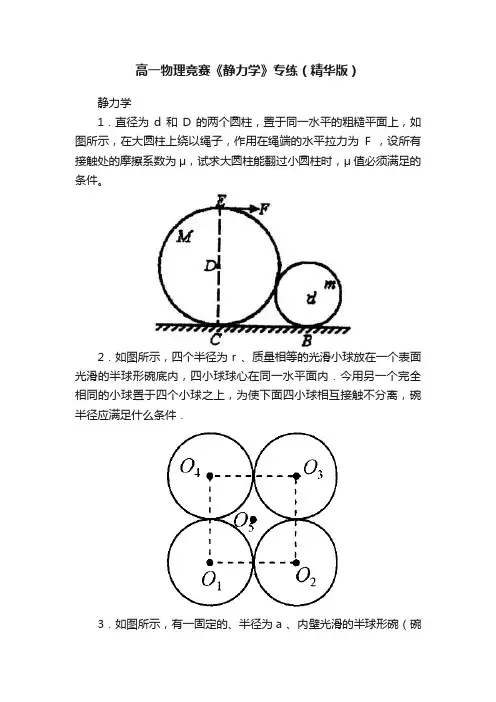
高一物理竞赛《静力学》专练(精华版)静力学1.直径为d 和D 的两个圆柱,置于同一水平的粗糙平面上,如图所示,在大圆柱上绕以绳子,作用在绳端的水平拉力为F ,设所有接触处的摩擦系数为μ,试求大圆柱能翻过小圆柱时,μ值必须满足的条件。
2.如图所示,四个半径为r 、质量相等的光滑小球放在一个表面光滑的半球形碗底内,四小球球心在同一水平面内.今用另一个完全相同的小球置于四个小球之上,为使下面四小球相互接触不分离,碗半径应满足什么条件.3.如图所示,有一固定的、半径为a 、内壁光滑的半球形碗(碗口处于水平位置),O 为球心。
碗内搁置一质量为m 、边长为a 的等边三角形均匀薄板ABC 。
板的顶点A 位于碗内最低点,碗的最低点处对A 有某种约束使顶点A 不能滑动(板只能绕A 点转动)。
(1).当三角形薄板达到平衡时,求出碗对顶点A 、B 、C 的作用力的大小各为多少。
(2).当板处于上述平衡状态时,若解除对A 点的约束,让它能在碗的内表面上从静止开始自由滑动,求此后薄板具有的最大动能。
4.一质量为m 的小球被固定在质量为M 的大圆环上.把此圆环挂在一不光滑的钉子上,如图所示.若要使环上的任何一点(除小球所在位置外)挂在钉子上,都能使环保持平衡,则环与钉子之间的摩擦系数μ至少多大?5.如图所示,将一支正六棱柱形铅笔放在斜面上,斜面倾角a=40°,铅笔与水平方面成θ角,铅笔静止,试问:(1)铅笔与斜面之间的静磨擦因数至少为多大?(2)θ角至少多大?6、一根细棒AB ,A 端用铰链与天花板相连,B 端用铰链与另一细棒BC 相连。
二棒长度相等,限于在图示的竖直面内运动,且不计较铰链处的磨擦。
当在C 端加一个适当的外力(与AB 、BC 在一个平面内)可使二棒静止在如图所示的位置,即二棒相互垂直,且C 端在A 端的正下方。
(1)不论二棒的质量如何,此外力只可能在哪个方向范围内?试说明理由。
(2)如果AB 棒质量为m 1,BC 棒质量为m 2,求此外力的大小和方向。

力、物体的平衡补充:杠杆平衡(即力矩平衡),对任意转动点都平衡。
一、力学中常见的三种力1.重力、重心①重心的定义:++++=g m g m gx m gx m x 212211,当坐标原点移到重心上,则两边的重力矩平衡。
②重心与质心不一定重合。
如很长的、竖直放置的杆,重心和质心不重合。
如将质量均匀的细杆AC (AB =BC =1m )的BC 部分对折,求重心。
以重心为转轴,两边的重力力矩平衡(不是重力相等):(0.5-x )2G =(x +0.25)2G ,得x =0.125m (离B 点). 或以A 点为转轴:0.5⨯2G +(1+0.5)2G =Gx ', 得x '=0.875m ,离B 点x =1-x '=0.125m.2.巴普斯定理:①质量分布均匀的平面薄板:垂直平面运动扫过的体积等于面积剩平面薄板重心通过和路程。
如质量分布均匀的半圆盘的质心离圆心的距离为x , 绕直径旋转一周,2321234R x R πππ⋅=,得π34R x = ②质量分布均匀的、在同一平面内的曲线:垂直曲线所在平面运动扫过的面积等于曲线长度剩曲线的重心通过路程。
如质量分布均匀的半圆形金属丝的质心离圆心的距离为x ,绕直径旋转一周,R x R πππ⋅=242,得πR x 2= 1. (1)半径R =30cm 的均匀圆板上挖出一个半径r =15cm的内切圆板,如图a 所示,求剩下部分的重心。
(2)如图b 所示是一个均匀三角形割去一个小三角形AB 'C ',而B 'C '//BC ,且∆AB 'C '的面积为原三角形面积的41,已知BC 边中线长度为L ,求剩下部分BCC 'B '的重心。
[答案:(1) 离圆心的距离6R ;(2)离底边中点的距离92L ] 解(1)分割法:在留下部分的右边对称处再挖去同样的一个圆,则它关于圆心对称,它的重心在圆心上,要求的重心就是这两块板的合重心,设板的面密度为η,重心离圆心的距离为x .有力矩平衡: ),2()2(])2(2[222x R R x R R -=-ηπηπ得6R x ==5cm. 填补法:在没挖去的圆上填上一块受”重力”方向向上的圆,相当于挖去部分的重力被抵消,其重心与挖去后的重心相同,同理可得6R x =. 能量守恒法:原圆板的重力势能等于留下部分的重力势能和挖去部分的重力势能之和,可得6R x =. (2) ∆AB 'C '的面积为原三角形面积的1/4,质量为原三角形质量的41,中线长度应为原三角形中线长度的21。


高中物理竞赛练习题静力学(预赛)一、共点力作用下物体的平衡1. 有两个质量分别为m1和m2的光滑小环,套在竖直放置且固定的光滑大环上,两环以细线相连,如图所示。
已知细线所对的圆心角为α,求系统平衡时细线与竖直方向间所夹的角θ为多少?2. 有一水平放置的半径R的圆柱体光滑槽面,其上放有两个半径均为r的光滑圆柱体A和B,如图所示为其截面图。
图中O为圆柱面的圆心,A、B分别为两圆柱的圆心,OQ为竖直线。
已知A、B两圆柱分别重G1和G2,且R=3r。
求此系统平衡时,OA线与OQ线之间的夹角α为多少?3. 四个半径均为R的光滑球,静止于一个水平放置的半球形碗内,该四球球心恰好在同一水平面上。
现将一个相同的第五个球放在前述四球之上,而此系统仍能维持平衡,求碗的半径为多少?4. 质量为m的立方块固定在弹簧上,两弹簧的劲度系数分别为k1和k2,未形变时长度分别为l1和l2,固定弹簧的另一端,使立方块可以沿水平面运动。
立方块与平面之间的动摩擦因数为μ,弹簧两固定点间距离为L,立方块大小可不计。
求立方块能够处于平衡状态的范围。
5. 两个质量相等的物体,用绳索通过滑轮加以连接,如图所示。
两物体和平面之间的动摩擦因数μ相等,试问要使这两个物体所组成的系统开始运动,角ϕ的最小值应为多少?(已知A 物体所在平面恰好水平)6. 半径为R 的刚性球固定在水平桌面上,有一个质量为M 的圆环状均匀弹性绳圈,原长2πa ,2R a =,绳圈的弹性系数为k (绳圈伸长s 时,绳中弹性张力为ks )。
将绳圈从球的正上方轻轻放到球上,并用手扶着绳圈使之保持水平并最后停留在某个静力平衡位置上,设此时绳圈长度为2πb ,b =,考虑重力,忽略摩擦,求绳圈的弹性系数k (用M 、R 、g 表示,g 为重力加速度)。
二、一般物体的平衡7. 圆桌面有三条相互等距的桌腿在圆桌边缘上支撑着,桌腿的重量忽略不计。
某人坐在正对着一套桌腿的圆桌边缘上,使圆桌以另两条桌腿着地点的连线为轴而倾倒,圆桌倾倒后,他再坐到桌面的最高点上,恰巧又能使圆桌恢复过来。

静力学1如图所示,一个半径为R 的四分之一光滑球面放在水平桌面上,球面上放置一光滑均匀铁链,其A 端固定在球面的顶点,B 端恰与桌面不接触,铁链单位长度的质量为ρ.试求铁链A 端受的拉力T. 2:图3—9中,半径为R 的圆盘固定不可转动,细绳不可伸长的圆盘固定不可转动,细绳不可伸长 但质量可忽略,绳下悬挂的两物体质量分别为M 、m.设圆盘与设圆盘与 绳间光滑接触,试求盘对绳的法向支持力线密度. 3、质量为m ,自然长度为2πa ,弹性系数为k 的弹性圈,水平置于半径为R 的固定刚性球上,不计摩擦。
而且a = R/2 。
(1)设平衡时圈长为2πb ,且b = 2a ,试求k 值;(2)若k = R2mg2p ,求弹性圈的平衡位置及长度。
求弹性圈的平衡位置及长度。
4、均质铁链如图2悬挂在天花板上,已知悬挂处的铁链的切线与天花板的夹角为θ,而铁链总重为G , 试求铁链最底处的张力。
试求铁链最底处的张力。
5、如图3所示,两不计大小的定滑轮被等高地固定在天花板上,跨过滑轮的轻绳悬挂三部分重物。
A 、B 部分的重量是固定的,分别是A G = 3牛顿和B G = 5牛顿,C G 则可以调节大小。
设绳足够长,试求能维持系统静止平衡的C G 取值范围。
取值范围。
6、如图5所示,长为L L 、粗细不均匀的横杆被两根轻绳水平悬挂,绳子与水平方向的夹角在图、粗细不均匀的横杆被两根轻绳水平悬挂,绳子与水平方向的夹角在图上已标示,求横杆的重心位置。
上已标示,求横杆的重心位置。
图 2θABC图 3OAB αβ第四个球,放在三个球的上方正中。
设四个球的表面、圆筒的内壁表面均由相同物质构成,其相互之间的最大静摩擦因数均为μ=0.775。
试问:R 取何值时,用手轻轻竖直向上提起,圆筒即能将四个球一起提起来? 12、物体放在水平面上,用与水平方向成30°的力拉物体时,物体匀速前进。
若此力大小不变,改为沿水平方向拉物体,物体仍能匀速前进,求物体与水平面之间的动摩擦因素μ。
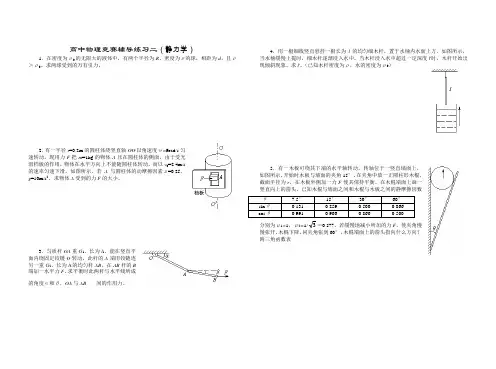
高中物理竞赛辅导练习二(静力学)1.在密度为ρ0的无限大的液体中,有两个半径为R、密度为ρ的球,相距为d,且ρ>ρ0。
求两球受到的万有引力。
2.有一半径r=0.2m的圆柱体绕竖直轴OO/以角速度ω=9rad/s匀速转动,现用力F把m=1kg的物体A压在圆柱体的侧面,由于受光滑档板的作用,物体在水平方向上不能随圆柱体转动,而以v0=2.4m/s的速率匀速下滑,如图所示。
若A与圆柱体的动摩擦因素μ=0.25,g=10m/s2。
求物体A受到的力F的大小。
3.匀质杆OA重G1、长为l1,能在竖直平面内绕固定铰链O转动,此杆的A端用铰链连另一重G2、长为l2的均匀杆AB,在AB杆的B端加一水平力F。
求平衡时此两杆与水平线所成的角度α和β,OA与AB间的作用力。
4.用一根细线竖直悬挂一根长为l的均匀细木杆,置于水桶内水面上方,如图所示,当水桶缓慢上提时,细木杆逐渐浸入水中。
当木杆浸入水中超过一定深度l'时,木杆开始出现倾斜现象。
求l'。
(已知木杆密度为ρ,水的密度为ρ0)5.有一木板可绕其下端的水平轴转动,转轴位于一竖直墙面上,如图所示,开始时木板与墙面的夹角15°,在夹角中放一正圆柱形木棍,截面半径为r,在木板外侧加一力F使其保持平衡。
在木棍端面上画一竖直向上的箭头。
已知木棍与墙面之间和木棍与木板之间的静摩擦因数分别为μ1=1,μ2=1/3≈0.577。
若缓慢地减小所加的力F,使夹角慢慢张开,木棍下降。
问夹角张到60°,木棍端面上的箭头指向什么方向?附三角函数表θ7.5°15°30°60°sinθ0.131 0.259 0.500 0.866cosθ0.991 0.966 0.866 0.500。

奥赛培训-静力学趣题(二)一、四个相同的球静止在光滑的大半球形碗内,它们的中心同在一水平面内,今以另一相同的球放在四球之上,若碗的半径大于球的半径k倍时,则四球将互相分离。
试求此k值。
(所有的接触面都是光滑的。
)二、一均匀圆桌面由三条相互等距的桌腿在圆桌边缘上支撑着,桌腿重量忽略不计。
某人坐在正对着一条桌腿的圆桌边上,恰好使圆桌以另两条桌腿着地点联机为轴而倾倒。
圆桌倾倒后他再坐到圆桌面的最高点上,恰好又能使圆桌恢复过来。
试求桌面半径与桌腿长度之比值。
三、如图1所示,一根细棒,上端A处用绞炼与天花板相连,下端B用绞炼与另一细棒相连,两棒长度相等,两棒只限于图示的垂直面内运动,且不计绞炼处的摩擦。
当在C端加一适当的外力(在纸面内)可使两棒平衡在图标位置处,即两棒间夹角为90°,且C端正处在A端的正下方。
试问:(1)不管两棒的质量如何,此外力只可能在哪个方向的范围内?(2)如果AB棒的质量1kg ,BC棒的质量2kg ,此外力的大小和方向若何?四、一空心圆环形圆管沿一条直径截成两部分,一半竖立在铅垂平面内,如图2所示,两管口处在一水平线上。
现向管内注入与管壁相切的小钢珠,左、右侧第一个钢珠都与圆管截面相切。
已知每个钢珠重W ,共2n个。
求从左边起第k个和第(k + 1)个钢珠之间相互作用的正向力量值N k。
假设系统中处处无摩擦。
五、如图3所示,一轻质木板EF长为L ,E端用铰炼固定在铅直墙面上,另一端用水平轻绳FD拉住。
木板上依次放着(2n + 1)个圆柱体,半径均为R ,每个圆柱体重量均为W ,木板与墙的夹角为α,一切摩擦都可略去,求FD绳上的张力T 。
六、如图4所示,代表某一铅直平面,在此面内有两根均匀细杆AB和BC ,质量相同,长度分别为l1和l2,它们共同接触水平地面,端点记为B ,各自的另一端A和C分别靠在相对的两堵垂直墙上。
已知墙面间距离为l ,且l>l1,l1>l2,且l1 + l2>l ,系统处处无摩擦。

与中学物理竞赛有关的静力学知识及试题知识准备1、重力:由于地球的吸引而使物体受到的力叫重力。
重力是地球对物体的万有引力在垂直当地水平面的一个分力,尤有引力的另一个指向地轴的分力为物化随同地球自转提供向心力。
一个物体的各部分受到地球对它的重力可以认为集中在一点,这一等效的作用点叫做物体的重心。
重心不一定在物体上,也不一定在物体的几何中心上。
求物体的重心有许多方法:(1)如果物体是一个平面,可以用悬持法确定物体的重心。
如果物体由几个部分组成,且每一个部分的重心容易求得,则由下面的公式求得整个物体的重心。
其方法是:(1)先建立一个直角坐标系,各部分的质量分别为:m 1、m 2、m 3、……,它们的坐标分别为()()()111222,,,,,,,,,n n n x y z x y z x y z ,则物体的重心(或质心)坐标为为: 112212112212112212i in n c n i in n c n i in n c n m xm x m x m x x m m m m m y m y m y m y y m m m m m z m z m z m z z m m m m⎧⎪+++⎪==+++⎪⎪⎪+++⎪==⎨+++⎪⎪⎪+++⎪==⎪+++⎪⎩∑∑∑ 2、弹力:A 、发生弹性形变的物体,会对迫使它形变的物体产生力的作用,这种力叫弹力。
弹力的方向:刚体间的弹力与接触面垂直(即沿接触面的法线方向),且由接触面指向受力物体所在的一方;B 、柔软的绳索对其他物体的作用力,沿绳且指向绳的收缩方向。
在弹性限度以内,弹性体的产生的弹力与弹性形变成正比(胡克定律),即F=kx ,式中的k 为弹性体的劲度系数。
(由弹性体的自身性质决定)。
C 、能发生明显形迹变的弹性体,在外界条件突然变化时,弹力的大小和方向不能产生瞬时突变。
而无明显形变的弹性体,它产生的弹力的大小和方向能发生瞬时突变。
3、摩擦力:当一个在另一个物体的表面上有相对运动或有相对运动趋势时,会产生阻碍两物体间的相对运动(或阻碍相对运动趋势)的力,叫滑动摩擦力(或叫做静摩擦力)。
静力学复习题1. 某平面任意力系向O 点简化,得到R ˊ=10N ,M 0=10 N·cm ,方向如图所示,求:该力系向A 点简化的结果。
2. 图示三铰刚架受力F 作用,求:A 、B 支座反力的大小。
3. 已知力P = 40 kN ,S =20kN ,物体与地面间的摩擦系数f = 0.5,动摩擦系数f ′= 0.4,求:物体所受的摩擦力。
4. 物块重W ,一外力F 作用在物块上,且作用线在摩擦角外,如图所示,已知ο25=θ,摩擦角ο20=m ϕ,F W =。
试确定物块的运动状态。
5. 力F 通过A (3,4,0),B (0,4,4)两点(长度单位为米),若F =100N ,求/;(1) 该力在y 轴上的投影;(2 )该力对z 轴的矩。
6. 已知力F 的大小,角度ϕ和θ,以及长方体的边长a ,b ,c ,求:(1)力F 在轴z 和y上的投影;(2)力F 对轴x 的矩)(F x m 。
7. 图示正立方体,各边长为a ,四个力1F 、2F 、3F 、4F 大小皆等于F ,如图所示,作用在相应的边上。
求:此力系简化的最终结果并在图中画出。
8. 等边三角形ABC.边长为a.己知四个力的大小相等,即F1=F2=F3=F4=F;力偶矩M=Fa, 则该力系简化的最后结果是什么?9. 图示结构,杆重不计.已知:L=4.5m. q0=3kN/m. P=6kN. M=4.5kNm.求固定端E处的反力.(作业二中4题)10 .图示结构,由杆AB、DE、BD组成,各杆自重不计,D、C、B均为铰链连接,A 端为固定端约束。
已知q(N/m),M=qa2(N·m),P=2qa(N),尺寸如图。
试列四个方程求固定端A的约束反力及BD杆所受的力。
(作业二中3题)11. .图示多跨梁由直杆AD和T字形杆DHG组成.已知:力P=2kN,q=0.5kN/m, M=4kNm,L=4m。
试列二个刚体静力学平衡方程求:支座H和支座C的反力。
第二部分:静力学一、复习基础知识点一、 考点内容1.力是物体间的相互作用,是物体发生形变和物体运动状态变化的原因。
2.重力是物体在地球表面附近所受到的地球对它的引力,重心。
3.形变与弹力,胡克定律。
4.静摩擦,最大静摩擦力。
5.滑动摩擦,滑动摩擦定律。
6.力是矢量,力的合成与分解。
7.平衡,共点力作用下物体的平衡。
二、 知识结构⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎩⎨⎧→→→⎩⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎪⎪⎭⎫ ⎝⎛--→⎪⎪⎭⎫ ⎝⎛→→⎪⎪⎩⎪⎪⎨⎧⎪⎪⎭⎫ ⎝⎛→⎪⎪⎭⎫ ⎝⎛-→的灵活使用方法:整体法和隔离法产生条件、摩擦力、弹力、重力顺序原则受力分析实效原则图解法(几何法)力的分解式法图解法(几何法)、公力的合成力的等效性使物体产生形变物体产生加速度)改变物体运动状态(使力的效果效果各异作用力与反作用力效果相同平衡力支持力等回复力、浮力、压力、动力、阻力:向心力、效果子力、电场力、磁场力不接触的力:重力、分产生条件、大小、方向力接触的力:弹力、摩擦性质力的种类物体受力物体同时定是施力物体施力物体同时定是受力相互性受力物体施力物体物体间作用物质性力的属性—物体间的相互作用—力的定义力.......321 三、 复习思路在复习力的概念时,同学们应注重回顾学过的各种具体的力,包括电磁学中的各种力,也可以联系牛顿第三定律展开研究力的相互性。
对于重力,在复习时可以联系万有引力定律,分清为什么“重力是由于地球的吸引而产生的力”。
且通过分析物体随地球自转需向心力,最终认识重力与万有引力之间的差异很小,一般可认为2地R GMmmg =。
摩擦力是本单元的重点,也是难点,要结合具体的例子,对摩擦力的大小和方向,摩擦力的有无的讨论以及物体在水平面、斜面上、竖直墙上等的滑动摩擦力与弹力的关系等,要分门别类地进行讨论、研究。
高中物理竞赛试题详解(2)1.如图1-32所示,求图示均匀薄板的重心,大正方形边长为a ,挖去的小正方形边长为4a ,一个顶点在大正方形的几何中心上,两正方形各对应边相互平行.1. [解]在大正方形中挖去一个与正方形O 1等大,关于正方形中心G 对称的小正方形O 2,则挖去小正方形后的大正方形,其中重心在G 点.其重量为正方形O 2的14倍.若设正方形O 2的质量为m ,则挖了O 2后的大正方形的质量为14m建立ox 坐标轴,根据对称性,重心必在ox 轴上.原点在O 点. 根据重心公式:112212n nnm r m r m r r m m m +++=+++142814m m r m m ⋅+⋅==+,即:重心在O 2O 1的连线上,离O 1的距离为120a . 2.如图1-33所示,边长为a 的均匀立方体,平衡地放在一个半径为r 的圆柱面顶部,假设静摩擦系数很大,足以阻止立方体下滑.试证明物体的稳定平衡的条件2a r >. 2.[解]若物体不能下滑, 由图可以看出,当正方体受到扰动时,其中心就由A 点移到B 点.只要B 点的位置比A 点高,正方体就处于稳定平衡状态.设:立方体与圆柱的接触点对应的半径转过了α角.如解图1-12所示.则:初始A 点的高度为2ar +,在B 点时的高度为:OM NR BS ++cos sin cos 2ar r αααα=+⋅⋅+()cos sin 2ar r ααα=++⋅⋅正方体处于平衡,须使()c o s s i n22aar r r ααα++⋅⋅>+ 整理得: (sin cos 1)(1cos )2ar αααα⋅+->-(tan )tan 222a r ααα->当α很小时,tan 22αα= 即只要2ar >时,正方体就处于稳定平衡状态.3.在蜡烛的底部插一个铁钉后,竖立在水中.蜡烛露出水面1cm ,已知蜡烛的密度为水密度的0.9倍.现将蜡烛点燃,蜡烛燃烧多长后方可熄灭? 3.解:设水的密度为ρ0蜡烛的密度为ρ,横截面积为s ,铁钉的质量为m图1-32O图1-33ar解图1-12A B OPM B PMαN N R S则: ρ0gsx =ρgs (x +1)+mgρ0gs (x -∆x )=ρgs (x -∆x )+mgρ0gsx =ρgs (1+∆x )∆x =10(cm )4.用20块质量均匀分布的相同光滑积木块,在光滑水平面上一块叠一块地搭成单孔桥,已知每一积木块长度为L .横截面是边长为4Lh =的正方形,要求此桥具有最大跨度(即桥孔底宽),试画出桥的示意图,并计算跨度s 与桥孔高度H 的比值。
静力学竞赛习题详解1.图1—23所示的上大下小的杯中,盛有密度均匀的混合液体.其密度为ρ经过一段时间后变成密度分别为ρ1,ρ2的两层均匀液体.如果总体积不变,试讨论杯底所受液体的压强有何变化?[解]: 取以杯底为底面积的竖直水柱为研究对象,在均匀混合时,该体积内两种密度的液体各占一半.而分层后,由于密度较大的一半液体分布在杯子的底部,由于平均底面积较小,而体的总高度不变,2.底边为a θ当θ动或翻倒.试分别求出发生滑动和翻倒时的θ,并说明在什么条件下出现的是滑动情况,在什么条件下出现的是翻倒情况.[解]物体恰好沿斜面下滑的条件是:sin cos mg mg θμθ=即tan μθ=若物体不下滑而翻倒,此时重心的延长线恰好过物体的左下角如图解2-2所示.此时角θ满足tan a bθ=若a u b <, 当1tan θμ-= 时, 先开始滑动.若a u b>, 当1tan a b θ-=时,先翻倒.3.一物体质量为m ,置于倾角为的斜面上,物体与斜面间的动摩擦4.一轻绳跨过两个等高的轻定滑轮,两端分别挂上质量m l =4kg 和m 2=2kg 的物体,如图1-25所示.在滑轮之间的绳上悬挂物体m ,为使三个物体能图1-25保持平衡,求m 的取值范围. [解]:m 最大值:的夹角α接近因此1m m <+ m 的最小值m 的夹角近90由此解得: m 综合以上:5.质量为M =1多少?[解]当物体在斜面运动时,物体所受的力并不在同一平面内.在垂直斜面的平面内,物体的受力如解2-5-1所示.沿斜面平面内受力如解2-5-2所示.由图可知。
N =mg cos30°因为物体做匀速直线运动,所以在两个方向合力都为0,即有21sin F f mg f θ=⎧⎨=⎩f 1、f 2分别为物体所受摩擦力的两个分量。
f 2解2-5-2f =求得f =又由f N μ=可求得μ=6.如图1-27线的夹角为θ[解]可。
竞赛作业2(静力学)姓名______________
1.如图所示,在半径为R的两个铁球内各挖一个半径为R/2的球腔C1和C2,两球腔与各球内切,两球心相距d,求两球间引力的大小(设铁球的密度为ρ)。
2.一薄壁烧杯,半径为R,质量为m,重心位于中心线上,离杯底为H,今将水慢慢注入杯中,问烧杯连同杯内的水共同重心最低时,水面离杯底的距离等于多少?为什么?(设水的密度为ρ)
3.如图所示,用铰链接在竖直墙上,悬挂物的重量为500N,轻杆OA,OB的长度都是50cm,AB=60cm,且A和B等高,均匀杆OC的倾角600,杆重200N,铰链C在AB中点正下方,CO⊥DO。
求(1)杆AO对墙作用力(2)OC对墙的作用力。
4.半径为R、质量为M1的均匀圆球与一质量为M2的重物分别用细绳AD和ACE悬挂于同一点A,并处于平衡状态,如图所示.已知悬点A到球心O的距离为L,不考虑绳的质量和绳与球的摩擦,试求悬挂圆球的绳AD与竖直方向AB间的夹角θ.(第十届全国中学生物理竞赛预赛试题)【15】
5.AO,CO,AD,BC,BO”,DO”为均匀钢片,可绕O,A,C,O’,
B,D,O”转动.由它们组成如图状铰链,AB与CD两端分别用绳连
接,下挂重物M,若知钢片条AO,CO,BO”,DO”质量均为m,AD,
BC的质量为2 m.问静止时绳子中的张力为多大?
6.半径为r、质量为m的三个相同的刚性球放在光滑的水平桌面上,两两互相接触。
用一个高为1.5r的圆柱形刚性园筒(上下均无底)将此三球套在筒内,园筒的半径取适当值,使得各球间以及球与筒壁之间均保持无形变接触。
现取一质量亦为m、半径为R的第四个球,放在三球上方的正中。
设四个球的表面、园筒的内壁表面均由相同物质构成,其相互之间的最
大静摩擦系数均为μ=(约等于0.775),问R取何值时,用手轻轻竖直向上提起园筒
即能将四个球一起提起来?。