用YΔ等效变换巧算复杂电路的等效电阻

计算一个电路的电阻，通常从欧姆定律出发，分析电路的串并联关系。

实际电路中，电阻的联接千变万化，我们需要运用各种方法，通过等效变换将复杂电路转换成简单直观的串并联电路。

本节主要介绍几种常用的计算复杂电路等效电阻的方法。

1、等势节点的断接法在一个复杂电路中，如果能找到一些完全对称的点（以两端连线为对称轴），那么可以将接在等电势节点间的导线或电阻或不含电源的支路断开（即去掉），也可以用导线或电阻或不含电源的支路将等电势节点连接起来，且不影响电路的等效性。

这种方法的关键在于找到等势点，然后分析元件间的串并联关系。

常用于由等值电阻组成的结构对称的电路。

【例题1】在图8-4甲所示的电路中，R 1 = R 2 = R 3 = R 4 = R 5 = R ，试求A 、B 两端的等效电阻R AB 。

模型分析：这是一个基本的等势缩点的事例，用到的是物理常识是：导线是等势体，用导线相连的点可以缩为一点。

将图8-4甲图中的A 、D 缩为一点A 后，成为图8-4乙图。

答案：R AB = 83R 。

【例题2】在图8-5甲所示的电路中，R 1 = 1Ω ，R 2 = 4Ω ，R 3 = 3Ω ，R 4 = 12Ω ，R 5 = 10Ω ，试求A 、B 两端的等效电阻R AB 。

模型分析：这就是所谓的桥式电路，这里先介绍简单的情形：将A 、B 两端接入电源，并假设R 5不存在，C 、D 两点的电势相等。

因此，将C 、D 缩为一点C 后，电路等效为图8-5乙对于图8-5的乙图，求R AB 是非常容易的。

事实上，只要满足21R R =43R R 的关系，该桥式电路平衡。

答案：R AB =415Ω 。

【例题3】在如图所示的有限网络中，每一小段导体的电阻均为R ，试求A 、B 两点之间的等效电阻R AB 。

【例题4】用导线连接成如图所示的框架，ABCD 是正四面体，每段导线的电阻都是1。

求AB 间的总电阻。

2、电流分布法 设有电流I 从A 点流入、B 点流出，应用电流分流的思想和网络中两点间不同路径等电压的思想，（即基耳霍夫定理），建立以网络中各支路的电流为未知量的方程组，解出各支路电流与总电流I 的关系，然后经任一路径计算A 、B 两点间的电压，再由即可求出等效电阻。

电阻的Ｙ形与△形联接及等效变换电路中电阻用串、并联方法化简为一个等效电阻。

这种电路不论有多少电阻，结构有多复杂，都能用串、并联方法化简为一个等效电阻的电路，称为简单电阻电路；但有些电路电阻与电阻的关系，既不串、也不并这种类型的电路称为复杂电阻电路。

对于这类电阻可用三角形网络等效变换为星形网络或星形网络等效变换为三角形网络的方法来分析。

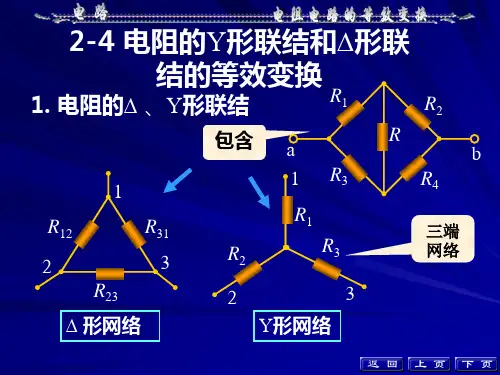
一、电阻的Ｙ形与△形联接的概念<?XML:NAMESPACE PREFIX = O />在电路中，有时电阻的联结即非串联又非并联，如图所示中，电阻<?XML:NAMESPACE PREFIX = V /> 的一端都接在一个公共结点上，各自的另一端则分别接到三个端子上，我们称此联结方式为Y形联结；电阻则分别接在三个端子的每两个之间，我们称之为三角形联结。

二、Y形和△形之间的等效变换如图所示，设它们对应端之间有相同电压如果它们彼此等效，则 对于图中联结的电路，各电阻中的电流分别为 对结点1、2、3分别列KCL方程，有（1） 而对图联结的电路，根据广义回路分别列KVL方程，有                又因  求解上述三个方程，可得出根据等效变换的原则，式（1）和式（2）中电压、和前面的系数应该相应地相等，故经整理后可得（3）上式就是从已知的联结电路的电阻来确定等效电路的各对应电阻的关系式。

也可整理成 （4）可见，上式就是从已知的联结电路的电阻来确定等效联结电路的各对应电阻的关系式。

第二章 电阻电路的等效变换2.1 学习要点1. 电阻的等效变换：电阻的串并联， Y 与△的等效变换。

2. 电源的串联、并联及等效变换。

3. “实际电源”的等效变换。

4. 输入电阻的求法。

2.2 内容提要 2.2.1 电阻的等效变换1. 电阻的串联：等效电阻： R eq ＝∑1=k nk R ；分压公式：u k ＝eqkeq ×R R u ； 2. 电阻的并联：等效电导：G eq ＝∑1=knk G ；分流公式：qe G G i i keq k ×=； 2.2.2. 电阻的Y 与△的等效变换1. △→Y ：一般公式：Y 形电阻＝形电阻之和形相邻电阻的乘积∆∆；即31232331*********231231212311++=++=++R R R R R R R R R R R R R R R R R R 2312＝2. Y →△：一般公式：形不相邻电阻形电阻两两乘积之和形电阻＝Y Y ∆；图 2.1即：213322131113322123313322112++=++=++=R R R R R R R R R R R R R R R R R R R R R R R R2.2.3 电源的串联、并联等效变换 电源的串联、并联等效变换见表2.1。

表2.1 电源的串联、并联等效变换2.2.4 “实际电源”的等效变换 1. “实际电压源”→“实际电流源” R i ＝R u 或 G i ＝1/R u i s ＝u s /R u 2. “实际电流源”→“实际电压源”R u ＝R i ＝1/G i u s ＝i s R i ＝i s /G i两者等效互换的原则是保持其端口的V AR 不变。

2.2.5 输入电阻的求法一端口无源网络输入电阻的定义（见图2.2）：R in ＝u/ i1. 当一端口无源网络由纯电阻构成时，可用电阻的 串并联、Y 形与△形等效变换化简求得。

2. 当一端口无源网络内含有受控源时，可采用外加电压法或外加电流法求得： 即输入电阻 R in ＝u s /i 或 R in ＝u/ i s方法是：在端口处加一电压源u s （或电流源i s ）, 再求比值u s /i 或u/ i s ，该比值即是一端口无源网络的输入电阻。

组织教学：清点人数，强调课堂纪律。

复习提问：1.受控源可分为哪几类？2.什么是转移电阻？什么是转移电导？导入新课：线性电阻和直流电源组成的电路称为直流线性电阻电路，简称直流电阻电路。

许多现实应用中的电阻电路都相当复杂，所以学习一些基本的分析方法就显得非常重要，通过学习这些方法，在电力、电信和无线电技术中，有许多工程的实际问题，都可以归结为电阻电路的计算问题，本节课我们首先介绍电阻的等效转换方法。

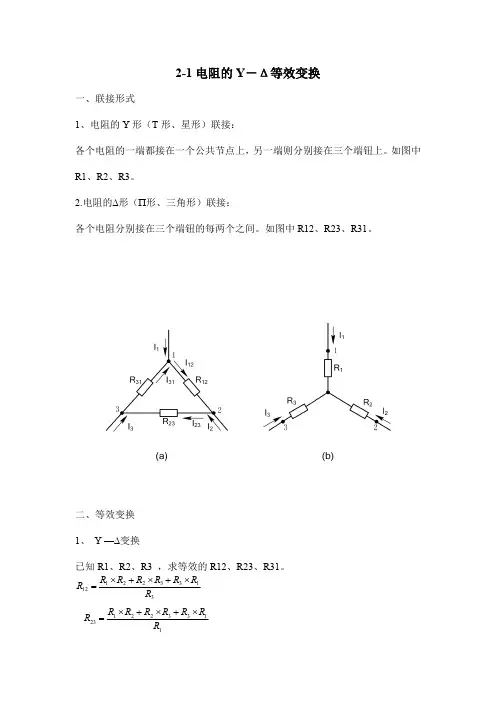
新授课：2-1电阻的Y－Δ等效变换一、联接形式1、电阻的Y形（T形、星形）联接：各个电阻的一端都接在一个公共节点上，另一端则分别接在三个端钮上。

如图中R1、R2、R3。

2.电阻的∆形（∏形、三角形）联接：各个电阻分别接在三个端钮的每两个之间。

如图中R12、R23、R31。

二、等效变换 1、 Y —∆变换已知R1、R2、R3 ，求等效的R12、R23、R31。

一般公式： 2、 ∆ —Y 变换：已知R12、R23、R31 ，求等效的R1、R2、R3 。

一般公式：313322112R R R R R R R R ⨯+⨯+⨯=113322123R R R R R R R R ⨯+⨯+⨯=213322131R R R R R R R R ⨯+⨯+⨯=对臂电阻单个相邻电阻之积的和=∆R 31231231121R R R R R R ++⨯=31231223122R R R R R R ++⨯=31231231233R R R R R R ++⨯=(a)(b)3、 特例，当三个电阻相等时： 课堂练习：1.下图2-10a 中的各个电阻阻值如图所示，求电路的等效电阻R ab 。

二．如图所示电路中, 已知U s=225V , R 0=1Ω, R 1=40Ω, R 2=36Ω, R 3=50Ω, R 4=55Ω, R 5=10Ω, 试求各电阻的电流。

周圈电阻之和相邻电阻之积=Y R ∆∆==R R R R Y Y 13或解 将△形连接的R 1, R 3, R 5等效变换为Y 形连接的R a, R c 、R d, 如图2.10(b)所示, 代入式(2.8)求得图2.10(b)是电阻混联网络, 串联的R c 、R 2的等效电阻R c2=40Ω, 串联的R d 、R 4的等效电阻R d4=60Ω, 二者并联的等效电阻R a 与R ob 串联, a 、b 间桥式电阻的等效电阻 桥式电阻的端口电流cb( a ) I I b( b )Ω=++⨯=++=Ω=++⨯=++=Ω=++⨯=++=5405010501044050101040204050104050135351355113513R R R R R R R R R R R R R R R R R R d c a Ω=+⨯=2460406040ab R Ω=+=442420i RR 2、R 4的电流各为 为了求得R 1、R 3、R 5的电流, 从图2.10(b)求得 回到图2.10(a )电路, 得 并由KCL 得小结：本节课我们学习重点在于电阻的星形和三角形连接之间的转换，同学们要熟练掌握两种连接方式的转换公式，做到从整体把握电路的化简方法。

y型三角形等效变换公式
Y型三角形等效变换公式，也称为Y等效变换公式，用于将一个Y 型三角形电路（由一根中性线和三根相位线组成）转换成等效的Δ型三角形电路（有三个角接点和三个线连接点）。

Y型三角形电路可以通过以下等效变换公式转换成Δ型三角形电路：
Va = Vab
Vb = Vbc
Vc = Vca
其中，Va、Vb和Vc分别表示Δ型三角形电路中的相电压，Vab、Vbc和Vca分别表示Y型三角形电路中的两两相电压。

类似地，可以通过以下等效变换公式将Δ型三角形电路转换成等效的Y型三角形电路：
Vab = Va - Vb
Vbc = Vb - Vc
Vca = Vc - Va
Y型三角形等效变换公式的拓展包括：
1.电流等效变换：除了电压，Y型三角形电路和Δ型三角形电路还可以通过类似的方式进行电流的等效变换。

2.电抗等效变换：除了电压和电流，Y型三角形电路和Δ型三角形电路还可以通过等效变换公式进行电抗的转换，包括电感和电容。

3.多阶段等效变换：当存在多个Y型三角形电路或多个Δ型三角形电路时，可以通过多次等效变换将它们转换成等效的大型电路。

这对于分析和设计复杂的三相电路非常有用。

4.等效变换的应用：Y型三角形等效变换公式在三相电力系统分析和电路设计中经常被使用，可以简化电路计算和分析的复杂性。

电阻的Y－△等效变换
“两个电路，有相同的连线端子，如果它们对应端子的电流方向和大小相同，对应两端子的电压方向和大小相同，则它们互为等效电路。

”如果把它们看成一个黑匣子，则它们的对外表现是相同的。

毫无疑问，两个等效电路内部必然有一个对应关系存在。

换句话说，对于如图电路，知道其中一个电路中的三个电阻，就可计算出另一个电路中的三个电阻。

从电路设计的角度看问题，要求各端子的电流大小和方向、两两端子的电压大小和方向的指标已确定，则起码有两种电路形式存在。

对于Y 型连接的电路。

根据KCL和KVL，写出三个独立方程：
i1+ i2+ i3＝0
R1i1－R2i2＝u12
R2i2－R3i3＝u23
将电流看做未知量，是一个三元一次方程组，解得：
对于△型连接的电路，端子1', 2', 3' 的电流为：
令：i1＝i'1，i2＝i'2，i3＝i'3，得：
对于任何的u12，u23，u31，上式都要成立，只能是其系数等于0 ，由此解得Y－△的等效电阻公式：
从上式也可解出△－Y的等效电阻公式：。

用Y/Δ等效变换巧算复杂电路的等效电阻钟佩文重庆市潼南中学，重庆 潼南 402660摘要：在某些复杂电路中，几个电阻既非串联，又非并联，如果使用常规方法计算它们的等效电阻，那么将会是一件十分困难繁琐的事情。

本文采用Y-Δ等效变换与Δ-Y 等效变换两种方法，将复杂电路中的Y 形联接与Δ形联接的电阻进行合理地互换，高效精确地计算电路的等效电阻，以达到事半功倍的效果。

关键词：Y-Δ等效变换；Δ-Y 等效变换；Y 形联接；Δ形联接；等效电阻在电路分析中，经常会遇到几个既非串联，又非并联的电阻组成的复杂电路。

要计算这个电路的等效电阻，如果单纯地采用串、并联规律的传统方法进行化简，那么运算过程将会非常困难繁琐。

本文重点介绍两种方法——Y-Δ等效变换与Δ-Y 等效变换，旨在找出复杂电路中Y 形联接与Δ形联接的电阻，将其进行合理地互换。

可使看似毫无规律的电阻呈现出简单的串、并联关系，在电路串并联基础上计算等效电阻，让复杂深奥的问题迎刃而解。

如图1中a 、b 所示，a 图为Y 形联接的电阻，b 图为Δ形联接的电阻，它们之间等效变换的条件是：仍然保持电路中其余各个部分的电流和电压不变，即要求对应端（如1,2,3）流入或流出的电流（如I 1,I 2,I 3）一一相等，对应端之间的电压（如U 12,U 23,U 13）一一相等。

当满足上述等效变换的条件时，在Y 形联接与Δ形联接两种接法中，对应2a3 I 1I 3b图1 Y 形联接与Δ形联接的电阻的任意两端的等效电阻也必然相等，即为：()23131223131221R R R R R R R R +++=+()23131213122332R R R R R R R R +++=+ ①()23131223121331R R R R R R R R +++=+联立三式，可以解出：将Y 形联接等效变换为Δ形联接时，331322112R R R R R R R R ++=131322123R R R R R R R R ++=②231322113R R R R R R R R ++=将Δ形联接等效变换为Y 形联接时，23131213121R R R R R R ++=23131223122R R R R R R ++=③23131223133R R R R R R ++=1、Y-Δ等效变换的实际应用 例题1 求解图2之中a 、b解析： 在图2所示的电路图Ⅰ中，5个阻值均为R 的电阻既非串联，又非并联，图2 电路图Ⅰb图3 a 、b 两点之间经过Y-Δ等效变换的电路图Ⅰ如果采用串、并联规律的传统方法进行化简，那么欲求它们的等效电阻将会变得非常复杂繁琐。

如何计算电路的等效电阻？
如何计算电路的等效电阻?
答：从你给的图中可得知，它们之间有并联、串联、复联的俗称混联电路。

为了便于计算我重新给电阻偏了统一的号，并添加了相应的电阻值，这样更有说服力。

（R1 50Ω）（R2 40Ω）（R3 10Ω）（R4 55Ω）（R5 36Ω）
求此类电路等效电阻的简单方法，就是将电路作丫/△等效互换，使它变为电阻串联、并联电路。

等效变换时，可以将R1. R2 R3的△形联演变成Y型联接，如下面图2所示。

根据电阻的△/丫等效变换公式可得：Ra=R1×R2/R1+R2+R3 =40x50/40+10+50=20Ω Rc=R1xR3/R1+R2+R3 =50×10/40+10+50=5Ω Rd=R2xR3/R1+R2+R3 =40×10/40+10+50=4Ω
将计算得出的Ra Rc Rd的阻值代入下列式中，可得a、b两点的等效电阻Rad=Ra+（Rc+R5∥Rd+R4）=20+（60×40/60+40）=44Ω
几十年的计算方法，可能使用起来不太方便，加上本人水平有限，难免有瑕疵，希望对提问者有一点帮助。

同时欢迎太家批评指正，在此谢过大家。

知足常乐2018.2.18湖北钟祥。

电阻Y形连接等效变换为△形连接的另一种计算方法
张智民
【期刊名称】《电世界》
【年(卷),期】2012(053)005
【摘要】电阻Y形连接变换为△形连接的等效电路图如图1所示。

【总页数】1页(P49-49)
【作者】张智民
【作者单位】中国石油天然气管道局,河北廊坊065000
【正文语种】中文
【中图分类】TM645.12
【相关文献】
1.电阻Y形与△形联接的等效变换的一种简单计算方法 [J], 姚祖恩
2.用顺次短接顺次断开法求电阻T形网络与π形网络的等效变换 [J], 高伟吉
3.T形和Π形电阻电路等效变换的教学探讨 [J], 田社平;孙盾;张峰
4.电阻星形(Y形)网络与三角形(△形)网络等效变换两种推导方法的比较 [J], 吕芳;李奋荣
5.电阻T形网络与π形网络等效变换的简单推导 [J], 董永胜
因版权原因，仅展示原文概要，查看原文内容请购买。