最优化问题的数学模型一般可以用约束集X和目标函数f进行表示.集合X

运筹学概念部分一、填空题1．运筹学的主要研究对象是各种有组织系统的管理问题,经营活动。

2．运筹学的核心主要是运用数学方法研究各种系统的优化途径及方案，为决策者提供科学决策的依据。

3．模型是一件实际事物或现实情况的代表或抽象.4通常对问题中变量值的限制称为约束条件，它可以表示成一个等式或不等式的集合。

5．运筹学研究和解决问题的基础是最优化技术，并强调系统整体优化功能.6．运筹学用系统的观点研究功能之间的关系。

7．运筹学研究和解决问题的优势是应用各学科交叉的方法，具有典型综合应用特性。

8．运筹学的发展趋势是进一步依赖于_计算机的应用和发展。

9．运筹学解决问题时首先要观察待决策问题所处的环境。

10．用运筹学分析与解决问题，是一个科学决策的过程。

11。

运筹学的主要目的在于求得一个合理运用人力、物力和财力的最佳方案.12．运筹学中所使用的模型是数学模型。

用运筹学解决问题的核心是建立数学模型,并对模型求解.13用运筹学解决问题时，要分析，定义待决策的问题。

14．运筹学的系统特征之一是用系统的观点研究功能关系.15。

数学模型中，“s·t”表示约束（subject to 的缩写）。

16．建立数学模型时，需要回答的问题有性能的客观量度，可控制因素，不可控因素。

17．运筹学的主要研究对象是各种有组织系统的管理问题及经营活动。

18. 1940年8月，英国管理部门成立了一个跨学科的11人的运筹学小组,该小组简称为OR。

二、单选题19．建立数学模型时，考虑可以由决策者控制的因素是（ A ）A．销售数量B．销售价格C．顾客的需求 D．竞争价格20．我们可以通过( C）来验证模型最优解。

A．观察B．应用C．实验D．调查21．建立运筹学模型的过程不包括（ A ）阶段。

A．观察环境B．数据分析C．模型设计D．模型实施22。

建立模型的一个基本理由是去揭晓那些重要的或有关的（B ）A数量B变量C约束条件 D 目标函数23。

1 2( ( ⎨最优化方法部分课后习题解答1.一直优化问题的数学模型为：习题一min f (x ) = (x − 3)2 + (x − 4)2⎧g (x ) = x − x − 5 ≥ 0 ⎪ 11 2 2 ⎪试用图解法求出：s .t . ⎨g 2 (x ) = −x 1 − x 2 + 5 ≥ 0 ⎪g (x ) = x ≥ 0 ⎪ 3 1 ⎪⎩g 4 (x ) = x 2 ≥ 0（1） 无约束最优点，并求出最优值。

（2） 约束最优点，并求出其最优值。

（3） 如果加一个等式约束 h (x ) = x 1 −x 2 = 0 ，其约束最优解是什么？ *解 ：（1）在无约束条件下， f (x ) 的可行域在整个 x 1 0x 2 平面上，不难看出，当 x =（3，4） 时， f (x ) 取最小值，即，最优点为 x * =（3，4）：且最优值为： f (x * ) =0（2）在约束条件下， f (x ) 的可行域为图中阴影部分所示，此时，求该问题的最优点就是在约束集合即可行域中找一点 (x 1 ,x 2 ) ，使其落在半径最小的同心圆上，显然，从图示中可以看出，当 x *=15 , 5 ) 时， f (x ) 所在的圆的半径最小。

4 4⎧g (x ) = x −x − 5 = 0⎧ 15 ⎪x 1 = 其中：点为 g 1 (x) 和 g 2 (x ) 的交点，令 ⎪ 1 1 2 ⎨2 求解得到： ⎨ 45即最优点为 x *= ⎪⎩g 2 (x ) = −x 1 −x 2 + 5 = 015 , 5 ) ：最优值为： f(x * ) = 65 ⎪x =⎪⎩ 2 44 48（3）.若增加一个等式约束，则由图可知，可行域为空集，即此时最优解不存在。

2.一个矩形无盖油箱的外部总面积限定为 S ，怎样设计可使油箱的容量最大？试列出这个优化问题的数学模型，并回答这属于几维的优化问题. 解：列出这个优化问题的数学模型为：max f (x ) = x 1x 2 x 3⎧x 1x 2 + 2x 2 x 3 + 2x 1x 3 ≤ S ⎪ s .t . ⎪x 1 > 0⎪x 2 > 0 ⎪⎩x 3 > 0该优化问题属于三维的优化问题。

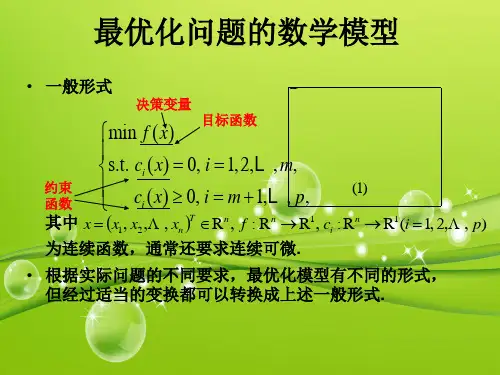
第4章离散优化模型【内容总结与思考】§1数学规划（最优化模型）概述。

规划模型（最优化模型）的三要素:决策（设计，控制）变量,约束条件和目标函数,最优化模型就是在满足约束条件的集合中（可行集）求目标函数的最优值。

按目标函数分分为多目标规划和单目标规划。

单目标规划模型的一般形式：max （min） Z = f（x）,x = （x{,x2,...,x n）Ts.t.（x） < 0, i = 1.2,...m线性规划:目标函数和约束条件都是线性的称为线性规划。

不是线性规划统称为非线性规划。

二次规划:目标函数是二次的，约束条件是线性的称为二次规划。

整数规划:决策变量均取整数值的规划称为整数规划。

部分决策变量取整数，其它取实数则称为混合整数规划。

只取0,1 的变量称为0-1变量。

实际问题建模（生产计划•线性规划）。

建模.软件计算，结果分析:对偶价格。

敏感性分析结果应用：系数变化范围（目标函数系数,约束右端项系数）例题1最优化模型的三姜素为（）■最优化问题就规划问题,整数规划是（)o§1生产计划建模:决策变量为目标为利润（费用），约束为生产要素限制，一般为线性规划。

例题1 一般的生产规划模型的目标函数是（），决策变量是（）,约束条件为（）。

其一般模型为（）§2运输问题建模（自来水输运与装机）lo 一般运输问题建模。

第，个供应点（源）第丿个需求点（汇）的量为®,则模型为m nmin（ max）i=l j=ln m ms.t. 2L x u -a i»Z x ij -lb j^x ij - ub j»j=l i=l i=l目标为费用最小（或利润最大），约束包括两类，供应约束（源点,始点）需求约束（终点•汇）。

一般运输问题的数据表结构:利润表+右边表示供应点的数据+底边表示各需求点的数据。

2O运输问题编程「水库送水问题Idefine set and variable;sets: gong/1..3/:a;xu/1..4/:bl f bu;link(gon g f xu):x f c;en dsets•evaluate to known variable;data:a=100,120,100;bl 二30,70,10,10;bu=80,140,30,50;c 二290,320,230,280,310,320,260,300,260,250,220,-1000;enddatamax=@sum(link(i,j):c(ij)*x(ij));@for(gong(i):@sum(xu(j):x(ij))<=a(i)); @for(xu(j):@sum(gong(i):x(ij))>=bl(j)); @for(xu(j):@sum(gong(i):x(ij))<=bu(j)); end例题1 一般运输问题的模型( 厂目标函数的形式为( )，约束条件是( )例题2 Lingo编程中重要的三部分是:set段，data段，和砂段。

最优化⽅法试卷及答案5套.docx《最优化⽅法》1⼀、填空题:1. _______________________________________________________ 最优化问题的数学模型⼀般为：_____________________________________________ ,其中___________ 称为⽬标函数，___________ 称为约束函数，可⾏域D可以表⽰为_______________________________ ，若 ________________________________ ，称/为问题的局部最优解，若为问题的全局最优解。

2.设f(x)= 2⽄+2“2-兀|+5花，则其梯度为__________ ^x = (l,2)r?6/ = (l,0)r,则f(x)在壬处沿⽅向d的⼀阶⽅向导数为___________ ，⼏何意义为_____________________________________ ，⼆阶⽅向导数为____________________ ,⼏何意义为_____________________________3.设严格凸⼆次规划形式为：min /(%) = 2兀］2 + 2x； - 2兀］-x2s.t. 2%! 4- x2 < 1> 0x2 > 0则其对偶规划为_______________________________________________min%（d ） = f （x k +ad k ）的最优步长为务=—叫）F.d kT Gd k2. （10分）证明凸规划min/（x ）,x G D （其中⼦（兀）为严格凸函数，D 是凸集）的最优解是唯⼀的3. （13分）考虑不等式约束问题min /（x ）s.t. c i （x ） < 0, Z G / = {1,2,…，加}其中/（x ）,6 （兀）a e /）具有连续的偏导数，设X 是约束问题的可⾏点，若在元处 d 满⾜巧（计<0,VC,（元）（可则d 是元处的可⾏下降⽅向。

《最优化方法》1一、填空题：1．最优化问题的数学模型一般为：____________________________，其中 ___________称为目标函数，___________称为约束函数，可行域D 可以表示 为_____________________________，若______________________________， 称*x 为问题的局部最优解，若_____________________________________，称*x 为问题的全局最优解。

2．设f(x)= 212121522x x x x x +-+，则其梯度为___________，海色矩阵___________,令,)0,1(,)2,1(T T d x ==则f(x)在x 处沿方向d 的一阶方向导数为___________，几何意义为___________________________________,二阶 方向导数为___________________，几何意义为_________________________ ___________________________________。

3．设严格凸二次规划形式为：012..222)(min 2121212221≥≥≤+--+=x x x x t s x x x x x f则其对偶规划为___________________________________________。

4．求解无约束最优化问题：n R x x f ∈),(min ，设k x 是不满足最优性条件的第k 步迭代点，则：用最速下降法求解时，搜索方向k d =___________ 用Newton 法求解时，搜索方向k d =___________ 用共轭梯度法求解时，搜索方向k d =___________________________________________________________________________。

练习题一1、建立优化模型应考虑哪些要素“答：决策变量、目标函数和约束条件。

2、讨论优化模型最优解的存在性、迭代算法的收敛性及停顿准则。

答：针对一般优化模型，讨论解的可行域，假设存在一()()min ()..0,1,2, 0,1,,i j f x s t g x i m h x j p≥===L L D 点，对于均有则称为优化模型最优解，最优解存在；*X D ∈X D ∀∈*()()f X f X ≤*X 迭代算法的收敛性是指迭代所得到的序列，满足，(1)(2)(),,,K X X X L L (1)()()()K K f X f X +≤则迭代法收敛；收敛的停顿准则有，，(1)()k k x x ε+-<(1)()()k k k x x xε+-<，，等等。

()()(1)()k k f x f x ε+-<()()()(1)()()k k k f x f x f x ε+-<()()k f x ε∇<练习题二1、*公司看中了例2.1中厂家所拥有的3种资源R 1、R2、和R 3，欲出价收购〔可能用于生产附加值更高的产品〕。

如果你是该公司的决策者，对这3种资源的收购报价是多少？〔该问题称为例2.1的对偶问题〕。

解：确定决策变量对3种资源报价作为本问题的决策变量。

123,,y y y 确定目标函数问题的目标很清楚——“收购价最小〞。

确定约束条件资源的报价至少应该高于原生产产品的利润，这样原厂家才可能卖。

因此有如下线性规划问题：123min 170100150w y y y =++*2、研究线性规划的对偶理论和方法〔包括对偶规划模型形式、对偶理论和对偶单纯形法〕。

答：略。

3、用单纯形法求解以下线性规划问题：〔1〕⎪⎪⎩⎪⎪⎨⎧≥≤+-≤++≤-++-=0,,43222..min32131321321321x x x x x x x x x x x t s x x x z ；〔2〕⎪⎪⎩⎪⎪⎨⎧=≥=++=+-=+-+-=)5,,2,1(052222..4min 53243232132 i x x x x x x x x x x t s x x z i 解：〔1〕引入松弛变量*4，*5，*6c j →1-11C B基b*1*2*3*4*5*60*421[1]-21000*532110100*64-101001c j -z j1-11因检验数σ2<0，故确定*2为换入非基变量，以*2的系数列的正分量对应去除常数列，最小比值所在行对应的基变量*4作为换出的基变量。

《最优化方法》1一、填空题：1．最优化问题的数学模型一般为：____________________________，其中 ___________称为目标函数，___________称为约束函数，可行域D 可以表示 为_____________________________，若______________________________， 称*x 为问题的局部最优解，若_____________________________________，称*x 为问题的全局最优解。

2．设f(x)= 212121522x x x x x +-+，则其梯度为___________，海色矩阵___________,令,)0,1(,)2,1(T T d x ==则f(x)在x 处沿方向d 的一阶方向导数为___________，几何意义为___________________________________,二阶 方向导数为___________________，几何意义为_________________________ ___________________________________。

3．设严格凸二次规划形式为：则其对偶规划为___________________________________________。

4．求解无约束最优化问题：n R x x f ∈),(min ，设k x 是不满足最优性条件的第k 步迭代点，则：用最速下降法求解时，搜索方向k d =___________用Newton 法求解时，搜索方向k d =___________用共轭梯度法求解时，搜索方向k d =___________________________________________________________________________。

二．（10分）简答题：试设计求解无约束优化问题的一般下降算法。

三．（25分）计算题1． （10分）用一阶必要和充分条件求解如下无约束优化问题的最优解：)1(632)(m in 21212131----=x x x x x x x f .2． （15分）用约束问题局部解的一阶必要条件和二阶充分条件求约束问题： 的最优解和相应的乘子。