当前位置：文档之家 › 《电路》第16章二端口网络解析

《电路》第16章二端口网络解析

  • 格式：ppt
  • 大小：1.96 MB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

16二端口网络

16二端口网络


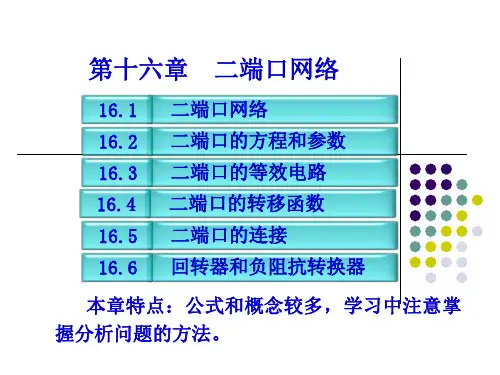
式中：△z = z11 z22 - z12z21、 △y = y11 y22 - y12y21
并非所有的二端口均有Z,Y 参数。

+

I1
Z

I2
+

U1 U 2 Z ( I1 I 2 )
Z Z Z Z Z
1
U1
U2

YZ
不存在
例16-2 求图中T形电路的Z参数。 解： 方法1：列电路方程法。
I2 y22 |U1 0 U2
入口短路时 的输出导纳
Y参数具有导纳的量纲, 而且是在端口短路的
情况下, 通过计算或测量得到的, 因此称为短路导
I1 y11 将Y方程写成矩阵形式为： I 2 y 21
纳参数。
y12 U 1 y 22 U 2
第十六章
二端口网络
本章内容
概述 两端口的参数和方程 两端口的等效电路 两端口的连接
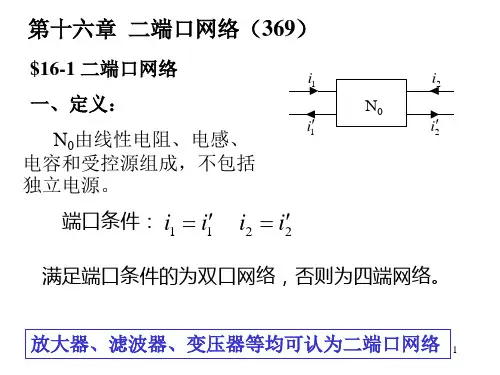
§16-1
二端口概述
在工程实际中，研究信号及能量的传输和信号变换时， 经常碰到如下形式的电路……四端网络。
R C C
滤波器
一. 端口 (port)
+ u1 i1 ′ i1 + u1 i1 i1′ i2 + u2
出端导纳
互易性和对称性
互易二端口：
对称二端口:
H12 H 21
H11 H 22 H12 H 21 1

I1

I2
+ R1
例题：求三极 管等效电路的 H参数
+

U1
β I1

R2 U 2
16-二端口网络解析

16-二端口网络解析


I1(s)0 Zb Zc
例2 求图示两端口的Z参数。
I1(s) Za
Zc
ZI1
(s) I
+
2
(s)
解
+
U1(s)
Zb
列KVL方程：
+
U2 (s)
U1(s) Za I1(s) Zb (I1(s) I2 (s)) (Za Zb )I1(s) Zb I2 (s)
U 2 (s) Zc I2 (s) Zb (I1(s) I2 (s)) ZI1(s) (Zb Z )I1(s) (Zb Zc )I2 (s)
2
U2 (s)
A
U1 ( s) U2 (s)
I2 (s)0
1.5
B
U1 ( s) I2(s)
U2 (s)0
4
C
I1(s) U2 (s)
I2 (s)0
0.5
D
I1(s) I2(s)
U2 (s)0
2
4. H 参数和方程
H 参数也称为混合参数，常用于晶体管等效电路。
① H参数和方程
UI21((ss))
[Z
]
Za
Z
b
Zb Z
Zb
Zb
Zc
3. T 参数和方程
I1(s)
① T 参数和方程 定义：
+
U1(s)
N
U1(s) AU2 (s) BI2 (s) I1(s) CU2 (s) DI2 (s)
I2 (s)
+
U2 (s)
U1 ( s)
I1
(
s)
T
U2 (s) I2 (s)
A B T C D
Y21
ch16电路分析解析

ch16电路分析解析


16-1 二端口网络
N
一端口（网络）
n:1 **
变压器
R
C
C
滤波器
三极管 反馈网络
传输线
放大器
N
涉及二端口（网络）
带反馈网络的放大器电路
一、二端口（网络）
必须满足端口条件： 从一个端钮流入的电流等于从另一个端钮流出的电流。
+ i1
u1 i1
N

i2 +
i2 u2 i1

i2
i3
N
输入端
二端口
输出端
0 U
1
Ya YYaa Yc YYcc

U
+
2 U2
0
U 2
I1 Y11U1 Y12U 2


I2
Y21U1
Y22U 2
Y11

I1 U 1
U2 0 Ya Yb
Y21

I2 U1
U 2 0
Yb
Y12

I1 U 2
U1 0
N0

I2
+
U2
分析前提：初始条件为零的线性无源二端口；
分析内容：关注端口VCR，即二端口参数方程；
采用相量法研究，参考方向如图所示。
2. Y参数和Y参数方程：

I1 I2
Y11U1 Y21U1
Y12U 2 Y22U 2[YFra bibliotek]
Y11 Y21
16-2 二端口的方程和参数
一、Y参数和方程
II 11
II 22
① Y参数方程
I1 I2

U1 U 2
第16章_02电路原理详解解析

第16章_02电路原理详解解析


•
•
YbU 1 (Y b Yc )U 2
Y11 Ya Yb Y12 Y 21 Yb Y 22 Yb Yc Ya Y11 Y12 Yb Y12 Yc Y22 Y12
T型等效电路求法:
已知二端口网络的Z参数为
Z11 Z21
Z12
Z22
求T型等效电路。
T型等效电路的Z参数应与给定的Z参数相同。
线性R、L、 C、M、受控源
+ u2 –
i1
i2
+ i1 u1 –
i2
线性R、L、 C、M、受控源
+ u2 –
i1
i2
注意 端口物理量4个
i1、i2、u1、u2
端口电压电流有六种不同的方程来表示，
即可用六套参数描述二端口网络。
i1
u1
u1
u2
i2
u2
i1
i2
u1
i1
i2
u2
•
•
•
I 1 Y11U 1 Y12 U 2
例1：绘出给定的Y参数的任意一种二端口等效电路。
Y
5 2
2 3
解 由矩阵可知： Y12 Y21 二端口是互易的。
故可用无源形二端口网络作为等效电路。
Ya Y11 Y12 52 3
Yc Y22 Y12 3 2 1
•
I1
+
•
U1
Yb
Ya
Yc
•
I2
+
•
U2
Yb Y12 2
通过形→T形变换可得T形等效电路。
16-3 二端口的等效电路
一个无源二端口网络可以用一个简单的 二端口等效模型来代替，要注意的是： 1.等效条件：等效模型的方程与原二端口网
电路课件 电路16 二端口网络

电路课件 电路16 二端口网络


12
16-2 二端口的方程和参数
Z参数计算或试验测量 (1)

设2-2’开路，即 由式(16-2)得：
只在1-1’施加电流源
图16-5(a)。
• Z11称2-2’开路时1-1’开路输入阻抗，Z21称2-2’开路 时 2-2’与1-1’间开路转移阻抗。
2019年2月3日星期日 第十六章 二端口网络
13

17
16-2 二端口的方程和参数
Z和Y参数及其他形式的参数





Y参数和Z参数都可用来描述二端口的端口外特性。 如一个二端口Y参数确定，一般可用式16-3求Z参数。反 之亦然(参阅表16-1)。 但许多工程实际问题中，希望找到一个端口电流、电压 与另一端口电流、电压间直接关系。如：放大器、滤波 器输入和输出间关系；传输线始端和终端间关系。 另外，有些二端口并不同时存在阻抗矩阵和导纳矩阵表 达式；或者既无阻抗矩阵表达式，又无导纳矩阵表达式。 如理想变压器属这类二端口。 意味着某些二端口宜用除Z和Y参数以外其他形式的参数 描述其端口外特性。

2019年2月3日星期日 第十六章 二端口网络
5
16-2 二端口的方程和参数

图16-2线性二端口。按正弦稳态情况考虑，用相量法 （可用运算法）。端口 1-1’ 和 2-2’ 处电流、电压相量 参考方向如图。设两端口电压 和 已知，可用替代定 理把两端口电压 和 看作外施独立电压源。根据叠 加定理， 和 分别等于各独立电压源单独作用时产生 电流之和，即

2019年2月3日星期日 第十六章 二端口网络
27
16-3 二端口的等效电路
给定二端口Z参数，确定等效T形电路

如给定二端口 Z 参数，确定等效 T 形电路 [ 图 16-8(a)] 中 Z1、Z2、Z3值，先写出T形电路回路电流方程 Z参数表示的网络方程式(16-2)中，由于Z12=Z21，将式 (16-2)改写为
第16章 二端口网络ppt课件

第16章 二端口网络ppt课件


–
1 Z 1 Z
Z1 1
Z2 1
1 Z
1
2 2
2 2
1
Y=
Z1+Z 21
Z1+Z
2
1 Z1+Z 21 Z1+Z
2
不存在Y参数
例3：
I1 1
8
U1
1
I1 8 1 U1
2
1
+ –
求二端口网络的Y参数
5 I2 方法一：根据参数的定义
2
2
解：① 将2—2 端
2I1
U2
短路 可以看出：2 、5 电阻
2
上无电流；受控电流源两 端无电压。
2、一般情况下，线性、无独立源的二端口网络 的独立参数有四个。但对互易的二端口网络，仅有三 个独立参数，对称的二端口网络，仅有两个独立参数。
3、选用二端口网络何种参数要看实际需要。并非 任何线性、无独立源二端口网络都能任选各种参数进 行分析，如理想变压器就没有Z参数和Y参数。
六、Z、Y、T、H参数之间的相互转换
= –Yb
U1 U2=0
= U2 U1=0
I2
Y21
= –Yb
= U1 U2=0
I2 Y22
=Yb+Y
= U2 U1=c0
Ya+Yb –Yb Y=
–Yb Yb+Y
c
网络中不含受控源时，Y12=Y21 只有三个独立参数。网络对称时 Y11=Y22，只有两个独立参数。
例2：
1 1
Z
2 2
Y
=
1
Z
–
1 Z
5
I2
Y11= I1 U1
=
U2=0
十六章 二端口网络

十六章 二端口网络


U 2
11
二端口网络的Y、Z参数特性：
1、对于线性R、L（M）、C元件构成的 任何无源二端口，Z12=Z21，Y12=Y21
2、对于对称的二端口，Z11=Z22，Y11=Y22 3、Z=Y-1参数
I 1 I 2
方法一：分别求Z四个 参数
+ -
+
-
U 1
第十六章 二端口网络（369）
$16-1 二端口网络 一、定义： N0由线性电阻、电感、 电容和受控源组成，不包括 独立电源。 端口条件： i1
i1
i1
i2
N0
i2
i1
i2 i2
满足端口条件的为双口网络，否则为四端网络。 放大器、滤波器、变压器等均可认为二端口网络
1
二端口网络分析特性： 1、对于二端口网络，主要分析端口的电流和电压， 不涉及内部电路的工作状况。因此，本章主要讨论 端口u、i为变量的电路方程（二端口VAR约束方程) 2、二端口网络端口有四个物理量(u1、i1、u2、i2）， 若其中两个为自变量，另两个为应变量，可有六组 表征网络特性的独立方程：
4
方法二：分别求出四个Y参数，从而得出Y矩阵
根据方程
1 Y1 1U 1 Y1 2U 2 I 2 Y2 1U 1 Y2 2U 2 I
0 ，U 1V，则如图 1、令 U 1 2
I Y1 2 1 U2
I 1 U 1
0 U 1
I 1
二、电流控制型二端口VAR方程
＋
I 1
U 1 －
No
＋
i2 ) u1 f(i1 , i2 ) u 2 f(i1 , 结构电 路 如 图
第16章二端口网络(电路 第五版)讲解

第16章二端口网络(电路 第五版)讲解

• 对无源线性二端口，T 参数只 有3个是独立的： AD -BC = 1 (为何不是B=C？)
• 对于对称二端口有A=D。
19
举例：求P438习题16-3图(c)
的T 参数矩阵。
解：由图得：
.
.
.
U.1=jwL1I.1+jwM I.2
U2=jwM I1+jwL2 I2
所以：
. I1=
1
jwM
. U2
+
L2 M
. (- I2 )
T=
. I1 1 .+ U1 Nhomakorabea1 1'
.
M
I2 2
+.
结束
L2 U2
-
2'
L1 M
jwL1L2
M
-jwM
1
L2
jwM
M
代入方程1
.
U1= jwL1
1
jwM
. U2 -
L2 M
. I2
.
+jwM I2
• 因AB-CD=1， 故只有3个参 数是独立的。
整. 理 U1=
L1 M
Z22 -Z12 -Z21 Z11
DZ= Z11 Z22 - Z12Z21
14
P423例16-2
. I1 ①
. ② I2
• 解：用电流源替代两
1 +
个端口电流。
.
Yb
. gU1
+
2
结束
.
• 由结点电压法
U1 Ya Yc
U2
.
..
I1 = (.Ya+Yb) U1-Y.bU2.
-
第十六章 二端口网络 92页PPT文档

第十六章 二端口网络 92页PPT文档

14
§16.2 二端口的参数和方程
上式称为 Z 参数方程，写成矩阵形式为：
Z
参数方程也可由
Y
参数方程解出

U1,U 2
得到， 即：
其中 △=Y11Y22–Y12Y21
15
§16.2 二端口的参数和方程
Z 参数矩阵与 Y 参数矩阵的关系为：
ZY1
16
§16.2 二端口的参数和方程
2、Z 参数的物理意义及计算和测定 在端口 1 上外施电流 I，1 把端口 2 开路，如图所示，由 Z 参数方程得：
级联是信号传输系统中最常见的联接方式。下图为两 个二端口的级联联接，前一个二端口的输入端联接前一个 二端口的输出端，即构成级联。
45
§16.3 二端口的连接
1、级联联接的条件：
显然，二端口的级联联接满足以下关系，
u1bu2a i1bi2a
46
§16.3 二端口的连接
2、级联联接的等效A参数：
（2）当仅由
I
2 作用时(I
＝
1
0
，电路N内部独立源均为零)，根据齐次定
理有
U (2) 1

z12 I 2
U
(2) 2

z22 I2
（3）当仅由电路N内部的独立源作用时，入口、出口均开路，有
U (3) 1

U OC1
U (3) 2

U OC 2
34
§16.2
根据叠加定理得
二端口的参数和方程
等效电路为
例，如下两图均为结构对称的，显然也是电气对称的。
例，如下图的结构不对称，但电气对称。
24
§16.2 二端口的参数和方程
四、T (A)参数和方程
第十六章-二端口网络解析精选课件PPT

第十六章-二端口网络解析精选课件PPT


对一个端口来说，从其一个端子流 1 i 入的电流一定等于从另一个端子流出的
电流，这种具有向外引出一对端子的电
路或网络称为一端口网络或二端网络。
i
1'
二、二端口网络
反馈网络
2021/3/2
制作群
放大器
4
主 页 总目录 章目录 上一页 下一页 退 出
§16-1 二端口网络
二端口的端口条件：
对于所有时间 t ，从端子1流入方 1 i1
§16-2 二端口的方程和参数
例2：求图示二端口的Y参数。
解： Y Y Y a a b U Y Y 1 b b U U Y 1 1 b Y Y Y b b U U c U 2 2 2 I I 1 1 I 2 g U 1 U-+11I1 Y b g U 1 Y b Y c U 2 I 2 1'
解：
方法一
1
Yb
2
Ya
Yc
I1 U 1Y a Y b I2 U1Yb
Y11UI11 U20 Ya Yb Y21UI21 U20 Yb
I2 U 2Y b Y c I1U2Yb
Y22UI22 U10 YbYc
Y12
2021/3/2
UI12
U10
Yb
制作群
ห้องสมุดไป่ตู้1'
2'
1 I1
Yb
I2 2
+
U1 Y a
Yc
-
1'
本章介绍的二端口：由线性电阻、电感(耦合电感)、 电容和线性受控源组成，并规定不含任何独立电源(如 用运算法分析时，其独立初始条件为零)。
2021/3/2
制作群
6
电路原理 第16章 二端口(网络)

电路原理 第16章 二端口(网络)


口网络，短路参数为Y
3 80
1 40
1 40
1 20
，求支路电流I1和I2。
解：列写回路方程为
R1I1 R2 I2
+U1 +U2
= Us =0
R1 I 1
US U1
I2
N U2
R2
II12
Y11U1 Y12U2 Y21U1 Y22U2
(R12YR211UY111)U(11RR21YY2122)UU22U0s
即：
I1 I2
Y11U 1 Y12U 2 Y21U 1 Y22U 2
Y 参数方程
写成矩阵形式为：
I1 I2
Y11 Y21
Y12
Y22
UU 12
[Y
]
Y11 Y21
Y12
Y22
Y参数值由内部参数及连接关系决定。
Y 参数矩阵.
（2） Y参数的物理意义及计算和测定
Y11 UI11 U 2 0 自导纳
端口电压电流有六种不同的方程来表示，即可用六套 参数描述二端口网络。
i1 u1 i2 u2
u1 u2 i1 i2
u1 i1 i2 u2
1. Y 参数和方程
•
（1）Y参数方程
I1
+
•
U1
N
•
I2
+ • U2
采用相量形式(正弦稳态)。将两个端口各施加一电压
源，则端口电流可视为这些电压源的叠加作用产生。
互易二端口： 对称二端口:
H12 H21 H11H22 H12H21 1
例3
•
I1
+
•
U1
R1
•
I2

第十六章 二端口网络

反馈 网络
放大器
2 、二端口网络
1
i1in
1
i2 in
2
u1
1 i1out
u2
i2out 2
(1)给定一个四端网络，若 i1in i1out , i2 in i2out , 则这个四端网络构成了二端口网络。 (2)二端口网络的对外联接特性由端口电压 u1 , u2 和电流 i1 , i2 确定。端口四个变量的相互关系可 通过二端口的参数和方程来描述，参数只决定于 二端口本身的元件及联接方式。
Z1 Z 2
[Z ]
Z2
Z2 Z2 Z3
例2：若上图中加上一个受控电压源，如图所示， 求二端口网络的Z参数。 Z I I Z1
1
3
2
U1
Z2 U R
3U R
U2
Z1
Z3
Z2 U R
I1
3U R
解： 方法一：
在左边端口加电流为 I1的电流源，右端开路，则： U1 U1 ( Z1 Z 2 ) I1 Z11 Z1 Z 2 I1 U2 U2 Z 2 I1 3 Z 2 I1 Z 21 4 Z 2 I1 在右边端口加电流为 I 2 的电流源，左端开路，则： U1 U1 Z 2 I 2 Z12 Z 2 I2 U2 U2 ( Z 2 Z 3 ) I 2 3 Z 2 I 2 Z 22 4 Z 2 Z 3 I2
直接列方程
1
Yc
2
I1 YaU1 Yb (U1 U2 ) (Ya Yb )U1 YbU2 I 2 YcU2 Yb (U2 U1 ) YbU1 (Yb Yc )U2

电路第五版课件 第十六章二端口网络


-Yb
(3)互易性和对称性 Y11 Y12 Y = 互易性：二端口满足： Y12 = Y21 Y21 Y22 . . I2 I1 Y21 = . Y12 = . . = Yb . = Yb U1 U2=0 U2 U1=0
1 . I1 1' Yb 1 + + . . U2 U1 2' 1' 2 Yb Ya Yc . I2 2'
. I1 . I2 .+ U1 线性 RLCM 受控源 +. U2
直接列方程法 . . . I1 = Y11 U1+ Y12 U2 . . . I2 = Y21 U1+ Y22 U2 写成矩阵形式： . . Y11 Y12 U1 I1 . = . I2 Y21 Y22 U2 Y11 Y12 Y 参数 Y = Y21 Y22 矩阵。 注意：Y 参数值由内部元 件参数及连接关系决定。
I 1 I
2
U 1 U
2
(1) Z参数方程定义 将两个端口各施加一 电流源，则端口电压可 视为电流源单独作用时 的叠加。
Z参数矩阵
注意：Z 参数值由内部元 件参数及连接关系决定。19
(2) Z参数的的物理意义及计算 开路法 . . . U1= Z11 I1 + Z12 I2 . . . U2= Z21 I1 + Z22 I2
Y11 Y12 Y21 Y22
11
Y =
例1：求P型电路的Y参数。 解法1：短路法 . Yb I1 1 Y11 = . . =Ya+Yb U1 U2=0 Ya Yc . I2 Y21 = . . = Yb 1' . U1 U2=0 Yb I1 . 1 + I1 . Y12 = . . = Yb Ya Yc U1 U2 U1=0 . 1' . I2 Y22 = . . =Yb+Yc Yb I1 U2 U1=0 1 Y = Ya+Yb

电路分析：二端口网络


二、压控型参数—短路导纳矩阵
1、对应的方程 以U1(s)、U2(s)为变量，即激励
II2 1((ss)) y y1 21 1 ((ss))U U1 1((ss)) yy122(2(ss))U U22((ss))
方程的矩阵式：
II1 2((ss))yy1 21 (1 (ss))
Y
Y 12 Y Y 11
Y
H
H 12
H 12
H 22
H 21
1
H 22 H 22
Y11 Y12 Y 21 Y 22
1
H 12
H 11
H 11
H 21
H
H 11
H 11
1 Y 12
Y 11
Y 11
Y 21
Y
Y 11
Y 11
H 11 H 12 H 21 H 22
Y 22 Y 21
三、混合型参数—混合参数矩阵
4、当二端口网络为线性非时变，且不
含受控源时，h12h21
5、注意：当以I1(s)、U2(s)为变量时， 得到的参数矩阵为逆混合参数矩阵H’
elecfans 电子发烧友 bbs.elecfans 电 子技术论坛
四、传输型—传输参数矩阵
1、对应的方程 以U2(s)、I2(s)为变量，即激励
出，在分析中又并不关心电路的内部 结构及内部各个支路的情况，而只讨 论外电路的状态与变化时，称该网络 为N端网络。elecfans 电子发烧友 bbs.elecfans 电
子技术论坛
2．N端口网络 如果一个网络有2N个端子向外
接出，这2N个端子又成对出现，即 端口处的输入电流等于输出电流时， 该网络可以视为一个N端口网络。
由（2）式得：
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

U2=0
U1 -
. I1
RLCM 受控源
线性 RLCM 受控源
. I2
Y12
=
I.1 U2
.
. 转移导纳；
U1=0
.+
. I1
线性
. I2
Y22
=
I.2 U2
U1
. 输入导纳。 -
U1=0
RLCM 受控源
Y短路导纳参数
2020年11月24日星期二
结束
+. U2 -
+. U2 -
+. U2 -
10
例1：求P型电路的Y参数。 1
1'
2020年11月24日星期二
Yb Ya Yc
Yb Ya Yc
Yb Ya Yc
2
结束
2' . I2 2
. U2=0
2' . I2 + 2
. U2 - 2'
11
(3)互易二端口(满足互易定理)
.
Y12
=
I.1 U2
. U1=0
.
Y21
=
I.2 U1
. U2=0
1 .ቤተ መጻሕፍቲ ባይዱ
+.
I1U1
1'-
Yb Ya Yc
N1
N不是二端口，而是四端网络。
i4 i2
+ u2 i2 -
N1 是否二端口？ ( 是 )
2020年11月24日星期二
6
3. 研究二端口网络的意义 ①应用广，其分析方法易推广应用于 n 端口网络； 结束 ②大网络可以分割成许多子网络(二端口)进行分析，
使分析简化；
③当仅研究端口的电压电流特性时，可以用二端口 网络的电路模型进行研究。
电路的结构和参数为已知，
可直接按定义分析计算。
.
Y11
=
I.1 U.1
. =Ya+Yb
U2=0
.
1' . I1
1+ .
Y21
=
I.2 U.1
Y12
=
I.1 U.2
.=
U2=0
-
I.2 I2
Yb
. = - Yb
U1=0
= - Yb
U1 1'-
. I1 1
. U1=0
Y22
=
I.2 U2
. U1=0
=Yb+Yc
4.分析方法 ①分析前提：讨论初始条件为零的线性无源二端
口网络； ②找出两个端口的电压、电流关系的独立网络方
程，这些方程通过一些参数来表示。
2020年11月24日星期二
7
§16-2 二端口的方程和参数
约定：
i1
①讨论范围是线性 R、L、C、M
与线性受控源，不含独立源。
+ u1 -
i1
②端口电压电流参考方向如图。
=
Y11 Y12 Y21 Y22
U.1 U2
[Y] = Y11 Y12 Y21 Y22
Y 参数 矩阵。
注意：Y 参数值由内 部元件参数及连接关
系决定。
9
(2)Y参数的物理意义及计算和测定.
.
短路法
I1
I2
.
.+
线性
Y11
=
I.1 U.1
Y21
=
I.2 U1
.
.
输入导纳；
U1 -
U2=0
. 转移导纳； . +
不对称的二端口，其电气特性可能是对称的，
这样的二端口也是对称二端口。
2020年11月24日星期二
13
例2：求图示二 端口的Y 参数。
解：
.
Y11
=
I.1 U1
. U2=0
= 1 = 0.2S (3//6)+3
.
Y21
=
I.2 U1
.=
U2=0
-
1. 3. I1 U1
= -0.0667S
i1
i2
+
+
u1
N
u2
- i1
i2 -
i2
i1
N
i3
i4
二端口
四端网络
2020年11月24日星期二
5
二端口的两个端口间若有外部连接，则会破坏
原二端口的端口条件。
结束
若在右图二端口网络的 端口间连接 R，则端口
iR i1 i3
N的条件被破坏。即
+
i3 = i1+ i ≠i1
u1
N
- i1
i4 = i2- i ≠i2
u1 - i1
N
电路为二端口网络。
i2
+ u2 i2 -
如果组成二端口的元件都是线性的，则称为线性 二端口；依据二个端口是否服从互易定理，分为 可逆的和不可逆的；
2020年11月24日星期二
4
使用时，若二个端口互换后不改变其外电
路的工作情况，则为对称二端口。
结束
注意：
二端口网络与四端网络的区别。
2020年11月24日星期二
12
(4)对称二端口 除满足 Y12 = Y21 外，
还满足 Y11 = Y22
Yb
1
2 结束
Ya Yc
1'
2'
在例1中，当Ya=Yc=Y 时 有Y11 = Y22 = Y+Yb
注意：对称二端口只有两个参数是独立的。
对称二端口是指两个端口电气特性上对称。
电路结构左右对称的一般为对称二端口。结构
3. 二端口电路方程的列写和求解。即二端口网络的 应用。
难点
1. 各参数方程之间的转换； 2. 含未知结构二端口的网络分析法； 3. 二端口的等效电路确定； 4. 二端口联接后参数方程的确定。
2020年11月24日星期二
2
§16-1 二端口网络
在工程实践中，研究信号及能量的传输、信
结束
号变换时，常遇到一些二端口电路：
R2 R1 - ∞
+ +
放大器
n:1 变压器
R CC
滤波器
2020年11月24日星期二
传输线
三极管
3
1. 端口
端口由一对端钮构成，且满足端
i
结束
口条件：即从端口的一个端钮流
+ u
N
入的电流必须等于从该端口的另 - i
一个端钮流出的电流。
2. 二端口
i1
当一个电路与外部电路通 +
过两个端口连接时，称此
2 . +. 结束 I2U2
- 2'
形式①：把激励与响应互换位置 互易二端口
后，端口电压电流满足关系：
.. I.1 = I.2 U2 U1
Y12 = Y21 如例1中有 Y12= Y21 = -Yb
对于由线性 R、L (M)、C 元件构成的任何无 源二端口，都具有互易性质。
互易二端口的四个参数中只有三个是独立的。
第十六章 二端口网络
结束
本章知识结构
二端口的 基本概念
二端口的参 数和方程
二端口参数 之间的转换
二端口 的等效
二端口的 T形、П 形等效
端口电压、 电流的计
算
二端口 的联接
回转器 和负阻 变换器
2020年11月24日星期二
1
重点
结束
1. 二端口的参数矩阵方程及其参数的求解方法；
2. 二端口的联接(级联、串联、并联) ；
I2
.+
线性
+.
U1
RLCM
U2
-
受控源
-
采用相量形式(正弦稳 态)。将两个端口各施 加一电压源，则端口 电流可视为电压源单 独作用时产生的电流 之和(叠加原理)。
2020年11月24日星期二
.
.
.
I.1 = Y11 U.1+ Y12U.2
结束
I2 = Y21U1+ Y22U2
写成矩阵形式：
.
.
I.1 I2
线性
RLCM 受控源
结束
i2
+ u2 i2 -
注意：端口物理量4个
i1、i2、u1、u2
端口电压电流有六种不同的方程来表示，
即可用六套参数描述二端口网络。
i1 u1 i2 u2
u1 u2
i1
i2
u1 i1 i2 u2
2020年11月24日星期二
8
1.Y(导纳)参数及方程
(1) Y参数方程
.
.
I1