下载文档原格式
第十六章二端口网络16二端网络口1-61二端口网络16-2 二口端方的程和参数1-6 二3端的等口电路1效6-4 端口二的移转数函61-5二端的连接口166 -转回和器负抗变阻换器16- 二端口网1一、络一口端网络+ iI+u- UiN I U +-U OC+-Z-Y I S二C、二端网口络a. 1i= i1’i2= i’21b 不.含包任独立何电c.源零状+ 态1u1ii ’11 -二口端网络i2i ’2+ u22- 2由线性RL、C及、线性受控源组成在复，频域是络工程实际题问常要常研究一网个的络对端钮之间的两系关16- 二2口的端方程和数参1+u111i-二端口络网i2+u2 2- 2电压、电关系流描述的用(量描述相) I 1 , I2 U1 , U2 U1 ,U 2 I , 1I2 U1I , 1U 2 , I 2 1I U 1 = Y Y 数参矩阵I U 22 U1 I1 = Z Z数矩参阵U I 2 2 U1 U 2 =T 参数矩T 阵I -I 1 2 , I I U, 1 U = H I 1 U 12 参数矩阵H 1 2 I 2 2 Uii1bi βibi o+ uo-+ u 1i11-二端口网络i2+2u2- 2+ iu-一Y参数方、(导纳程数参矩)阵1 方、程导的出11 LTII+ U1I 2 20N U 2 1I = 1Y U1 +1Y1 2 U 2 I 2 =Y 211U +Y 22U 2 I1 Y11 Y1 2 U 1 = I 2Y Y12 2 2 U 2- 1 2、参2的数义含(路导纳参短数) I 2 12I 1LT I+ U1-N021IY 1 1= U1 U 20=1端2-2口短路，端口11-的入端导纳端2-口2 短路正，向移导转纳I2 2Y1= 1U2 =01UI1 TIL 0NI2 2+- 2U I1 = Y11 U1 + Y12U 2 I =2Y 1U12 +22 U 21Y2 I2Y22 = 2U I 1Y1 =2 U 2 U =01口1-1 端路，短端2口2 的-端入纳端导口11 短-路，反转向移导U1 纳0=例1Y求数。
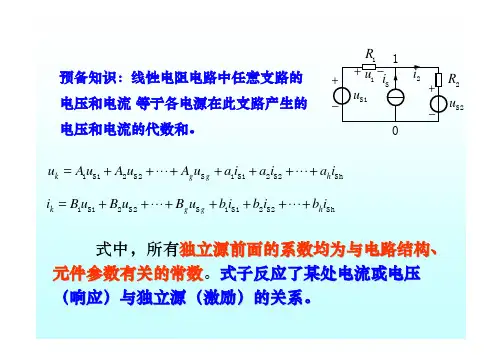
第16章二端口网络1．求图16-1所示二端口的Y参数、Z参数和T参数矩阵。
图16-1解：（1）图16-1（a），两端口电压和电流参考方向，如图16-2（a）所示。
根据各元件的特性及电路的KVL和KCL定理，可得：将式②代入式①得：综上可得：图16-2（2）图16-1（b），两端口电压和电流参考方向，如图16-2（b）所示。
根据各元件的特性及电路的KVL和KCL定理，可得：将式②代入式①得：综上可得：2．求图16-3所示二端口的Y参数和Z参数矩阵。
图16-3解：图16-3所示电路为纯电阻电路，所以只求Z即可。
（1）图16-3（a），将三个电阻为1Ω的三角形电路转换为星形电路，如图16-4（a）所示，可得：所以（a）（b）图16-4（2）图16-3（b），电流电压方向如图16-4（b）所示，则有：又根据电路的对称特点可得：所以3．求图16-5所示二端口的T参数矩阵。
图16-5解：图16-6是五个二端口电路，分别标出了端口电压、，电流、及其参考方向。
图16-6（1）图16-6（a），，所以T参数矩阵为（2）图16-6（b），，所以T参数矩阵为（3）图16-6（c），建立KVL方程：整理得：所以T参数矩阵为：（4）图16-6（d），，所以T参数矩阵为（5）图16-6（e），，所以T参数矩阵为。
4．求图16-7所示二端口的Y参数矩阵。
图16-7解：图16-8是两个二端口电路，分别标出了端口电压、，电流、及其参考方向。
图16-8（1）图16-8（a），网孔电流方程为：所以Y参数矩阵为：（2）图16-8（b），结点电压方程为：。
第十六章（二端口网络）习题答案选择题1、ffi示n 掃口的2参数£B 、C 、3G 答案：AC 1.5S0.5S 0.5S 1.5SD0.5S1.5S 0.5S答案：B3.图示二端口网络的F 参数矩阵中r 叛（答案：C5、设两个无源二端口 P,P 的传输参数分别为匚八则当两个无源二端口级联时,•其复合二端口的传输鉢r 为：（）B. T-TC 、T +T答案：D答案：A7x 对线性无源二制口而言，以下关系式正确的是（答案：B2.图示二端口的F 参数为：＜A -0.5S 1.5S0.5S-1.5SB 0.5S -1.5S -0.5S 1.5S A.1 r B. C 、 1D 、~T答案:BZ2D,1.5S4＞图示二端口网络的N 参魏e 阵中右区 为：（lo<■3A 、2 +Z ,ZBs 2 ,2 C> Z ,2 +ZD 、Q2D 、 丁丁6,在对称二端口网络的F 参数矩阵中，只有（）个参数是独立的。
Ax 2个CxD 、4个C>A^HD 、H =F答案：B10.将两个无源二端口 £严串联时，其复合二端口的参数为：（AvD 、7 + r答案: 二、填空题8.若两个传输参数都为 ■3 42'3 的二端口级联，则级联后复合二端口传输参数矩阵为（ A. 飞 4-B, 9 4'£ 16 9JG 17 12'D 、 12 IJ 1 ™24 1717 24答案: C49B.亠身胡G3Ci3 F12 D\ 2^^— 79、若e 知二4崗口传输参数矩阵T ・ A 、严 £ 1c 、-mQ；，则图示T 型等效电路参数2忆忆依次分别为C 、 1.图 16 — 3 （a ）所示二端口电路的 Y 参数矩阵为丫=〔丫丫I 图16—3 （ b ）所示二端口的 Z 参数矩阵为k 丫」Z=E Z图1A32 •图16—4所示二端口网络的 丫参数矩阵是丫 =「1 3 7L 6_11 6 2 3」 602Qk L 51 节。
电路教案第16章二端口网络教学目标：1.了解二端口电路的基本概念和特性。
2.掌握二端口网络的矩阵描述方法。
3.掌握二端口网络的参数化描述方法。
教学准备：教材、讲义、黑板、白板、投影仪、计算机、实验装置等。
教学过程：一、引入（10分钟）1.教师通过提问的方式，引导学生回顾一端口电路的内容。
2.通过引入实际生活中的例子，如声学系统、通信系统等，引导学生了解二端口电路的概念。
二、理论讲解（40分钟）1.二端口电路的基本概念和特性：a.什么是二端口电路？b.二端口电路的输入端口和输出端口。
c.二端口电路的参数：传输参数、散射参数、互阻参数和互导参数。
d.二端口电路的特性：传输特性、散射特性。
2.二端口网络的矩阵描述方法：a.传输矩阵（ABCD参数）的定义和计算方法。
b.传输矩阵的特性和应用。
3.二端口网络的参数化描述方法：a.K参数的定义和计算方法。
b.K参数的特性和应用。
三、实例分析（30分钟）1.教师通过实例分析的方式，讲解如何使用传输矩阵和K参数对二端口网络进行分析和设计。
2.学生根据所学知识，结合实例进行讨论，加深对二端口电路的理解和应用能力。
四、实践操作（30分钟）1.学生根据教师的指导，使用实验装置进行实验操作。
2.学生通过实验，掌握使用传输矩阵和K参数对二端口电路进行测量和分析的方法和技巧。
五、小结（10分钟）1.回顾本节课的学习内容和重点。
2.强调二端口电路的重要性和应用领域。
3.鼓励学生在日常学习中多进行实践操作，提高实际应用能力。
教学反思：本节课通过引入实际例子，结合理论讲解和实例分析，使学生对二端口电路有了更深入的了解。
通过实践操作，让学生掌握了使用传输矩阵和K参数对二端口电路进行测量和分析的方法和技巧。
但由于时间限制，实践操作可能不够充分，需要在后续的教学中加强实践环节。
)习题解答(第十六章二端口网络一、选择题1．二端口电路的a 。
参数方程是H????????IU?HH?UU?IH?HI21111111112122b． a ．????????UI?H?HI?HUU?HI??22222122112221????????IH??HUUH?IUI?H21112121222111d．． c ????????I??UHIU?IH?HUH??22221222112121b —161所示二端口网络的Z参数方程为。
．图2j4j43?j4???j43????．b；a；．????j1??j4j1j4??????j43?j4j43j4??????cd．；．????j1?j4?j4j1????T。
d 参数应满足3．无任何电源的线性二端口电路的1BC?BCAD???BC?AD1DA?．b．．cda．c 联接，其端口条件总是满足的。
4．两个二端口三种、cba ．串联b．并联c．级联d．、a．图516—2所示理想变压器的各电压、电流之间满足的关系为d 。
iiuu111111n???n?? b ； a ．．，；，uinuni2222iiuu111111n?n????d．．c，；；，uinuni2222二、填空题Y?Y??3，图=参数矩阵为Y）所示二端口电路的（316．图1—a Y16—??Y?Y??ZZ??）所示二端口的b（Z参数矩阵为Z=。
??ZZ??6113????Y2．图Y 参数矩阵是。
16—4所示二端口网络的??3627???6?2三角形连接的电阻，则电路416—中三个星形连接的电阻等效为三个解：将图a416a如图164—（）所示。
由图—（）得：UUU?11211?UI?U??1216663U?UUU1141??2122U4U?????4I?I???UU??2111226616633??72UU?=213661?13??Y =于是??3627??g10??T所示回转器的5—3．图16参数矩阵为。
第十六章(二端口网络)习题解答
一、选择题
1．二端口电路的H 参数方程是 a 。
a ．⎩⎨⎧+=+=22212122121111U H I H I U H I H U
b ． ⎩⎨⎧+=+=22212122
121111I H U H U I H U H I
c ．⎩⎨⎧+=+=22222112122111U H I H U U H I H I
d ． ⎩⎨⎧+=+=2
2212112
121112I H U H I I H U H U
2．图16—1所示二端口网络的Z 参数方程为 b 。
a ．⎥⎦⎤⎢⎣⎡---+j1j4j4j43；
b ．⎥⎦
⎤⎢⎣⎡----j1j4j4j43；
c ．⎥⎦⎤⎢⎣⎡--j1j4j4j43；
d ．⎥⎦
⎤⎢⎣⎡--+j1j4j4j43
3．无任何电源的线性二端口电路的T 参数应满足 d 。
a ．D A =
b ．C B =
c ．1=-AD BC
d ．1=-BC AD 4．两个二端口 c 联接，其端口条件总是满足的。
a ．串联
b ．并联
c ．级联
d ．a 、b 、c 三种 5．图16—2所示理想变压器的各电压、电流之间满足的关系为 d 。
a ．
n u u 121=，n i i =2
1
；
b ．
n u u =21，n
i i
121-=；
c ．
n u u 121-=，n i i
=2
1；
d ．
n u u =21，n
i i
121=； 二、填空题
1．图16—3（a ）所示二端口电路的Y 参数矩阵为Y =
⎥⎦
⎤⎢⎣
⎡--Y Y Y Y
，图16—3
（b ）所示二端口的Z 参数矩阵为Z =
⎥⎦
⎤⎢⎣⎡Z Z Z Z。
2．图16—4所示二端口网络的Y 参数矩阵是Y =
⎥⎦
⎤⎢⎣⎡-32676131。
解：将图16—4中三个Ω2星形连接的电阻等效为三个Ω6三角形连接的电阻，则电路如图16—4（a ）所示。
由图16—4（a ）得： 212111613166U U U U U I -=-+=
⎪⎭⎫ ⎝⎛-++-=-+++=21211
221226131434616641U U U U U U U I U I
=213
267U U +
于是 Y =⎥⎦
⎤
⎢⎣⎡-32676131
3．图16—5所示回转器的T 参数矩阵为
⎥⎦
⎤
⎢⎣⎡010g g 。
解：由回转器两个端口电压、电流的关系，得
211i g u -=， 121i g
u = 即 211i g
u -=， 21gu i =
由此可见 T =⎥
⎦
⎤
⎢⎣⎡010g g
4．图16—6所示的二端口网络中，设子二端口网络1N 的传输参数矩阵为⎥
⎦
⎤
⎢⎣⎡D C B A ，则复合二端口网络的传输参数矩阵为⎥⎦⎤
⎢
⎣⎡
++D BY C AY B A 。
解：图16—6所示的二端口网络可看成由1N 和虚线框中的二端口级连而成。
虚线框中的二端口的传输参数矩阵为⎥
⎦
⎤
⎢
⎣⎡101Y 。
设图16—6所示二端口网络的传输参数矩阵为T ，则 T = ⎥⎦⎤⎢⎣⎡101Y ⎥⎦⎤⎢⎣⎡⋅D C B A =⎥⎦
⎤⎢⎣⎡++D BY C AY B A
5．图16—7所示二端口网络的Y 参数矩阵为 ⎥⎦
⎤
⎢⎣⎡∆∆-∆-∆12n n n ，式中
212R R n +=∆ 。
解：由图16—7得：
3111U I R U += …… ① 4222U I R U += …… ② 3
4
U n U
= …… ③ 2
1I n I -= …… ④ 从以上四式中消去3
U ，4U 和2I 得 2212121221
U R R n n U R R n n I +-+= 消去3
U ，4U 和1I 得 22
121212
2
1U R R n U R R n n I +++-= 因此 Y =⎥
⎦
⎤⎢⎣⎡∆∆-∆-∆12n n n ，式中 212
R R n +=∆ 三、计算题
1．图16—8所示二端口网络的Z 参数是Ω=1011Z 、Ω=1512Z 、Ω=521Z ，
Ω=2022Z 。
试求s U U 2。
解：由给定的Z 参数得
2111510I I U += …… ①
212205I I U += …… ②
由输入、输出端口得
11100U I U s += …… ③ 2225I U -= …… ④
由①、③得 2115110I I U s += 由②、④得 219I I -=
于是 2222239)25(3997515)9(110U I I I I U s =-⨯=-=+-⨯=
即 39
12=s U U
2．已知某二端口的Y 参数矩阵为Y ⎥
⎦
⎤
⎢⎣⎡--=3225S ，求其π形等效电路（如图16—9所示）中的1Y 、2Y 、3Y 。
解：由题目给出的Y 参数矩阵得
⎩⎨⎧+-=-=212
2
113225U U I U U I 而图16—9的Y 参数方程为
⎩⎨⎧++-=-+=2
321222
21211)()(U Y Y U Y I U Y U Y Y I
对照上述两组方程得
521=+Y Y ，332=+Y Y ，22-=-Y 故 S 22=Y ，S 31=Y ，S 13=Y
3．已知图16—10所示二端口S N 的Z 参数为Ω=100
11Z ，Ω-=50012Z ，Ω=32110Z ，Ω=1022Z ，求：L Z 等于多少时其吸收功率最大。
解：将L Z 以左的部分视为一端口电路，那么当L Z 和此一端口电路匹配时L Z 可获得最大功率，计算此一端口电路戴维南阻抗的等效电路如图16—10（a ）。
由给定的条件可得
211500100I I U -=，212101000I I U +=，1
1500I U -= 从以上三式中消去1U 和1I ，得325302
2=I
U ，因此 Ω=32530L Z 4．求图16—11所示二端口网络的T 参数。
解：图16—11所示的二端口网络可视为三个子二端口网络级连而成。
设左、中、右三个子二端口网络的传输参数矩阵分别为T 1 ，T 2 ，T 3 则
T 1 ⎥⎦⎤⎢⎣⎡=010g g ， T 2 ⎥⎦⎤⎢⎣⎡=n n 100， T 3 ⎥
⎦
⎤
⎢⎣⎡=1101R
而 T = T 1 T 2 T 3 ⎥⎦⎤⎢
⎣⎡=010g g ⎥
⎦
⎤
⎢⎣⎡n n 100⎥⎦⎤⎢⎣⎡1101R ⎥⎦⎤
⎢⎣
⎡=0)(1)(1ng ng ngR 5．电路如图16—12所示，试求用H 参数表示的双端接二端口电压转移函数s
U U
2。
解：由H 参数方程及端口外电路的伏安关系 ⎪⎩
⎪⎨⎧-=+=-=+=z s s R
U U H I H I I Z U U H I H U 222212121
2121111
从上两式中消去1
I 得 s s z
U U H Z H R H H =⎥⎦
⎤⎢⎣
⎡+⎪⎭
⎫ ⎝⎛+-211222112)(11 ∴ )
(11122211221
2H Z H R H H H U U
s z s
+⎪⎭
⎫
⎝⎛+-=。
