第16章二端口网络(丘关源)

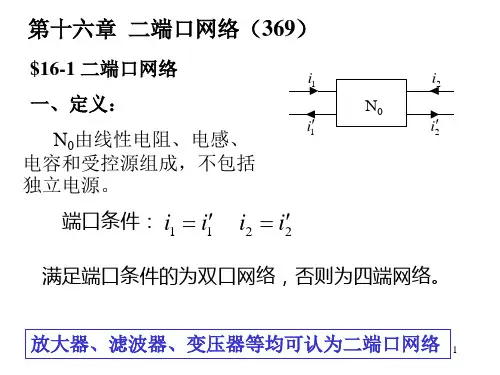
第十六章 二端口网络16.1 基本概念16.1.1 二端口网络的端口条件和端口变量1. 端口条件：在端口网络的任意端口上，由一端流入的电流必须等于由另一端流出的电流，这叫做双口网络的端口条件；2. 端口变量：包括两个端口电压21u u ，和两个端口电流21i i ，。

16.1.2 二端口网络的方程和参数二端口网络的对外电气性能可以用一些参数表示。

即以这些参数组成的方程对外电路表示二端口网络的电气性能。

在分析二端口的参数时，按正弦稳态情况考虑。

本章讨论的二端口是由线性电阻、电感、电容和线性受控源组成，不含任何独立电源。

如图16-1所示为一线性二端口。

11'22'116-图1. Y 参数方程用21U U ∙∙，表示21I I ∙∙，（1） 方程⎪⎩⎪⎨⎧+=+=∙∙∙∙∙∙22212122121111U Y U Y I U Y U Y I （2） 参数的物理意义。

分别把入口和出口短路出口的驱动点导纳导纳入口与出口之间的转移导纳出口与入口之间的转移入口的驱动点导纳----=----=----=----==∙∙=∙∙=∙∙=∙∙∙∙∙∙22220211201221011111122U U U U U I Y U I Y U I Y U I Y由于以上参数是在入口和出口分别短路情况下的参数，所以称为短路参数。

对于线性无源网络（指即不包含独立电源，也不包含受控源），2111Y Y =，只有三个独立参数，又称互易双口；当2211Y Y =时，称为对称双口，只有两个独立参数。

2. Z 参数方程用∙∙21I I ，表示∙∙21U U ，（1）⎪⎩⎪⎨⎧+=+=∙∙∙∙∙∙22212122121111I Z I Z U I Z I Z U （2）参数的物理意义。

分别把入口和出口开路，出口驱动点阻抗入口对出口的转移阻抗出口对入口的转移阻抗入口驱动点阻抗----=----=----=----==∙∙=∙∙=∙∙=∙∙∙∙∙∙22220211201221011111122I I I I I U Z I U Z I U Z I U Z对于互易双口，2112Z Z = ，只有三个独立参数；对于对称双口，1211Z Z =，只有两个独立参数。

第16章二端口网络1．求图16-1所示二端口的Y参数、Z参数和T参数矩阵。

图16-1解：（1）图16-1（a），两端口电压和电流参考方向，如图16-2（a）所示。

根据各元件的特性及电路的KVL和KCL定理，可得：将式②代入式①得：综上可得：图16-2（2）图16-1（b），两端口电压和电流参考方向，如图16-2（b）所示。

根据各元件的特性及电路的KVL和KCL定理，可得：将式②代入式①得：综上可得：2．求图16-3所示二端口的Y参数和Z参数矩阵。

图16-3解：图16-3所示电路为纯电阻电路，所以只求Z即可。

（1）图16-3（a），将三个电阻为1Ω的三角形电路转换为星形电路，如图16-4（a）所示，可得：所以（a）（b）图16-4（2）图16-3（b），电流电压方向如图16-4（b）所示，则有：又根据电路的对称特点可得：所以3．求图16-5所示二端口的T参数矩阵。

图16-5解：图16-6是五个二端口电路，分别标出了端口电压、，电流、及其参考方向。

图16-6（1）图16-6（a），，所以T参数矩阵为（2）图16-6（b），，所以T参数矩阵为（3）图16-6（c），建立KVL方程：整理得：所以T参数矩阵为：（4）图16-6（d），，所以T参数矩阵为（5）图16-6（e），，所以T参数矩阵为。

4．求图16-7所示二端口的Y参数矩阵。

图16-7解：图16-8是两个二端口电路，分别标出了端口电压、，电流、及其参考方向。

图16-8（1）图16-8（a），网孔电流方程为：所以Y参数矩阵为：（2）图16-8（b），结点电压方程为：。

第十六章（二端口网络）习题答案选择题1、ffi示n 掃口的2参数£B 、C 、3G 答案：AC 1.5S0.5S 0.5S 1.5SD0.5S1.5S 0.5S答案：B3.图示二端口网络的F 参数矩阵中r 叛（答案：C5、设两个无源二端口 P,P 的传输参数分别为匚八则当两个无源二端口级联时,•其复合二端口的传输鉢r 为：（）B. T-TC 、T +T答案：D答案：A7x 对线性无源二制口而言，以下关系式正确的是（答案：B2.图示二端口的F 参数为：＜A -0.5S 1.5S0.5S-1.5SB 0.5S -1.5S -0.5S 1.5S A.1 r B. C 、 1D 、~T答案:BZ2D,1.5S4＞图示二端口网络的N 参魏e 阵中右区 为：（lo<■3A 、2 +Z ,ZBs 2 ,2 C> Z ,2 +ZD 、Q2D 、 丁丁6,在对称二端口网络的F 参数矩阵中，只有（）个参数是独立的。

Ax 2个CxD 、4个C>A^HD 、H =F答案：B10.将两个无源二端口 £严串联时，其复合二端口的参数为：（AvD 、7 + r答案: 二、填空题8.若两个传输参数都为 ■3 42'3 的二端口级联，则级联后复合二端口传输参数矩阵为（ A. 飞 4-B, 9 4'£ 16 9JG 17 12'D 、 12 IJ 1 ™24 1717 24答案: C49B.亠身胡G3Ci3 F12 D\ 2^^— 79、若e 知二4崗口传输参数矩阵T ・ A 、严 £ 1c 、-mQ；，则图示T 型等效电路参数2忆忆依次分别为C 、 1.图 16 — 3 （a ）所示二端口电路的 Y 参数矩阵为丫=〔丫丫I 图16—3 （ b ）所示二端口的 Z 参数矩阵为k 丫」Z=E Z图1A32 •图16—4所示二端口网络的 丫参数矩阵是丫 =「1 3 7L 6_11 6 2 3」 602Qk L 51 节。

电路教案第16章二端口网络教学目标：1.了解二端口电路的基本概念和特性。

2.掌握二端口网络的矩阵描述方法。

3.掌握二端口网络的参数化描述方法。

教学准备：教材、讲义、黑板、白板、投影仪、计算机、实验装置等。

教学过程：一、引入（10分钟）1.教师通过提问的方式，引导学生回顾一端口电路的内容。

2.通过引入实际生活中的例子，如声学系统、通信系统等，引导学生了解二端口电路的概念。

二、理论讲解（40分钟）1.二端口电路的基本概念和特性：a.什么是二端口电路？b.二端口电路的输入端口和输出端口。

c.二端口电路的参数：传输参数、散射参数、互阻参数和互导参数。

d.二端口电路的特性：传输特性、散射特性。

2.二端口网络的矩阵描述方法：a.传输矩阵（ABCD参数）的定义和计算方法。

b.传输矩阵的特性和应用。

3.二端口网络的参数化描述方法：a.K参数的定义和计算方法。

b.K参数的特性和应用。

三、实例分析（30分钟）1.教师通过实例分析的方式，讲解如何使用传输矩阵和K参数对二端口网络进行分析和设计。

2.学生根据所学知识，结合实例进行讨论，加深对二端口电路的理解和应用能力。

四、实践操作（30分钟）1.学生根据教师的指导，使用实验装置进行实验操作。

2.学生通过实验，掌握使用传输矩阵和K参数对二端口电路进行测量和分析的方法和技巧。

五、小结（10分钟）1.回顾本节课的学习内容和重点。

2.强调二端口电路的重要性和应用领域。

3.鼓励学生在日常学习中多进行实践操作，提高实际应用能力。

教学反思：本节课通过引入实际例子，结合理论讲解和实例分析，使学生对二端口电路有了更深入的了解。

通过实践操作，让学生掌握了使用传输矩阵和K参数对二端口电路进行测量和分析的方法和技巧。

但由于时间限制，实践操作可能不够充分，需要在后续的教学中加强实践环节。

Chapter 16 二端口网络主要内容1.二端口网络及其方程；2.二端口的H A T Z,Y, ),( 参数矩阵及其相互关系；3.转移函数，T 型 和 型等效电路；4.二端口的连接；5.回转器和负阻抗变换器。

§16-1二端口网络端口：从端子1流入的电流等于从端子1' 流出的电流，则1- 1' 两个端子构成一个端口。

二端口网络（双口网络）：1- 1'一对端子为输入端子，2- 2' 一对端子为输出端子，以便与其他设备相联接。

变压器、滤波器、运算放大器等均属于双口网络。

本章所研究的二端口网络，由线性元件C M L R , ( ,）互感及受控源组成, 不含有独立电源和初始值构成的附加电源，当网络不含受控源时，成为无源线性双口网络。

§16-2 二端口网络的方程及参数用二端口概念分析电路, 仅对二个端口处的电流、电压之间的关系感兴趣。

一、Y 参数方程（短路参数）⎩⎨⎧+=+=22212122121111U Y U Y I U Y U Y I⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⇒21212221121121 U U U U Y Y Y Y I I Y⎥⎦⎤⎢⎣⎡22211211 Y Y Y Y def Y Y 参数矩阵，短路导纳矩阵 1.短路导纳参数的测定022220211201221011111122, , ,========U U U U U IY U IY U IY U I Y例16－1： 求下图所示二端口的Y 参数。

解：① 把端口2- 2` 短路, 则()- - 0122112011111122b U b b a U b a Y UI Y Y U I Y Y U I Y Y Y U I ===+==+===② 把端口1-1` 短路，则()bU b b c U b c Y UI Y Y U I Y Y U I Y Y Y U I -===+==+===0211221022222211-2.Y 参数的特点① 根据互易定理，由线性 C M L R ),( , 构成的任何无源二端口，2112Y Y =，故一个无源线性二端口，只要3个独立的参数足以表征其性能；② 对称二端口，2211Y Y =, 则此二端口的二个端口1- 1` 和2- 2` 互换位置后，其外部特性不会有任何变化；对称二端口中, 因 2211Y Y =，2112Y Y =故其 Y 参数中只有两个是独立的。