平面的投影特性

2-2 点、线、面的投影特性一、点的投影1、点的三面投影点是组成物体最基本的几何元素。

如图2-9所示，在三投影面体系中，由空间点A（x，y，z）分别向三投影面作正投影，得其三面投影a（x，y）、a′(x，z）、a″（y，z），即过点A分别作三投影面的垂线，其垂足即为点A的三面投影；展开H面和W面，得到点A的三视图：a 、a′长对正，a′、a″高平齐，a 、a″宽相等，如图2-10所示。

图2-9 点的三面投影图2-10 点的三视图例1 ：已知空间点B的两面投影b ，b′，如图2-11所示，求其第三面投影b″。

分析：空间点B的三面投影b 、b′、b″符合“长对正，高平齐，宽相等”的投影规律。

作图： b′与b″高平齐，b与b″宽相等，则其交点即为b″。

图2-11 求点的第三面投影图2-12 求点的三面投影例2 ：已知空间点D(5,4,3)，如图2-12所示,求其三面投影。

分析：空间点D的三面投影分别为d（x，y）、d′（x，z）、d″（y，z），且符合“长对正，高平齐，宽相等”的投影规律。

作图：分别在三投影轴上取x1=5，y1=4，z1=3，按“长对正，高平齐，宽相等”的投影规律分别作直线段，交点即为空间点D的三面投影（d 、d′、d″）。

2、两点的相对位置空间两点的相对位置是指空间两点间前后、左右、上下的位置关系。

两点在空间的相对位置可以根据两点的坐标值来判定，如图2-13所示。

X坐标确定两点的左右位置关系。

X坐标值大的点在左；Y坐标确定两点的前后位置关系。

Y坐标值大的点在前；Z坐标确定两点的上下位置关系。

Z坐标值大的点在上。

图2-13 两点的相对位置故A点在B点的右，后，上方，即B点在A点的左，前，下方。

3、重影点及其可见性判断若空间两点在某一投影面上的投影重合，则称这两点为该投影面的重影点。

此时，这两点位于同一投射线上，且有两个坐标的值分别相等，不等值的坐标之大小可以确定重影点的可见性，即X、Y、Z坐标值大的点分别位于左方、前方、上方，为可见点，如图2-14所示。

平面的投影由初等几何学可知，不在一条直线上的三点、一条直线和线外一点、两平行直线、两相交直线可决定一平面；在投影图上可利用几何元素来表示平面。

但是形体上任何一个平面图形都有一定的形状、大小和位置。

从形状上看，常见的平面图形有三角形、矩形、正多边形等直线轮廓的平面图形。

平面的表示方法1．不在一条直线上的三点；2．一条直线和线外一点；3．两平行直线；4．两相交直线；5．任意一平面图形。

图2—21几何元素表示平面平面形在三面投影体系中的特性平面形的投影一般仍为平面形，特殊情况下为一条直线。

平面形投影的作图方法是将图形轮廓线上的一系列点（多边形则是其顶点）向投影面投影，即得平面形投影。

三角形是最简单的平面形，如图2—25所示，将△ABC三顶点向三投影面进行投影的直观图和三面投影图。

其各投影即为三角形之各顶点的同面投影的连线。

其它多边形的作法与此类似。

又此可见，唨平面形的投影，实质上仍是以点的投影为基础而得的投影。

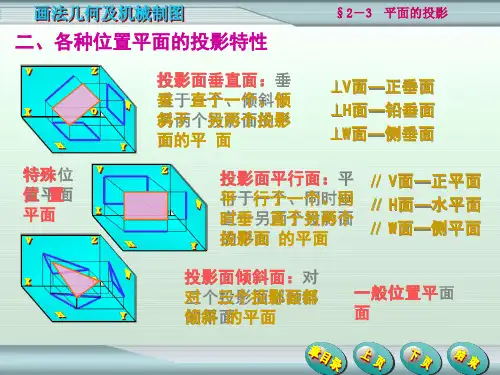
图2—22一般位置平面的投影图2—23投影面平行面的投影特性平面形在三面投影体系中的位置可分为三种：1．一般位置平面——对于三个投影面都倾斜平面对三个投影面都倾斜的平面，称为一般位置平面，如图图2—22所示。

一般位置的三角形平面的投影情况，由于它对三个投影面都倾斜，所以三个投影仍为三角形，且不反映实形，都比实形缩小了。

由此得到一般位置平面的投影特性：（1）类似性——在三个投影面上的投影均为相仿的平面图形，且形状缩小；（2）判断——平面的三面投影都是类似的几何图形，该平面一定是一般位置平面。

2．投影面平行面——平行于一个投影面的平面平行于一个投影面也即同时垂直于其它两个投影面的平面，称为投影面平行面。

如图2—23所示，投影面平行面有三种：水平面（∥H面）、正平面（∥V面）、侧平面（∥W面）。

三种投影面平行面的投影特征：（1）真实性——如平面用平面形表示，则在其所平行的投影面上的投影，反映平面形的实形；（2）积聚性——在另外两个投影面上的投影为直线段（有积聚性）且平行于相应的投影轴；（3）判断——若在平面形的投影中，同时有两个投影分别积聚成平行于投影轴的直线，而只有一个投影为平面形，则此平面平行于该投影所在的那个投影面。

直线、平面在三面投影体系中的投影特性分析【摘要】建筑制图中直线、平面相对于三个投影面的不同位置关系的分类相同，空间直线按其相对于三个投影面的不同位置关系可分为三种：投影面平行线、投影面垂直线和投影面倾斜线。

【关键词】相对位置；投影特性；分析一、投影面平行线与投影面平行面1.定义的区别（1）投影面平行线：与一个面平行与另外两个面倾斜，按其与水平投影面、正立投影平面、侧立投影平面平行的位置分为水平线、正平线、侧平线。

（2）投影面平行面：与一个面平行与另外两个面垂直，按其与水平投影面、正立投影平面、侧立投影平面平行的位置分为水平面、正平面、侧平面。

2.投影特性的区别（1）投影面平行线：直线在所平行的投影面上的投影反映实长，此投影与投影轴的夹角反映直线与另两个投影面的夹角实形；直线在另两个投影面上的投影，平行于相应的投影轴，但不反映实长。

“开发资产管理应用程序时，我们首要任务之一是帮助客户完全掌控过程知识。

为此，我们首次允许用户灵活地借助收集的情报快速创建自己的资产模型。

”ABB设备管理和资产优化全球产品经理NeilShah说到，“包括根本原因分析在内的资产分析是帮助客户在当今工业市场中保持竞争力的另一个关键因素。

”（2）投影面平行面：平面在它平行的投影面上的投影反映实形，其它两个投影积聚成线段，并且分别平行于相应的投影轴。

3.空间位置的判别（1）投影面平行线：一斜两直线，必为平行线；斜线在哪面，平行哪个面。

（2）投影面平行面：一框两直线，必为平行面；框在哪个面，平行哪个面。

投影面平行线投影图投影面平行面投影图二、投影面垂直线与投影面垂直面1.定义的区别众所周知，信息化条件下的现代战争，武器装备的优劣在很大程度上影响战争的胜败，但是决定战场胜负的主体因素依然是人。

现代战争中的每一项军事行动，都离不开军人良好身体素质的支撑。

良好身体素质的获得自然离不开真、难、严、实的军事训练，而逼近实战的军事训练中也将不可避免的发生军事训练伤。

学习要求§5.1 平面表示法§5.2 平面的投影特性第五章平面本章目录§5.3 平面内的点和直线第五章平面平面投影平面的投影有两种表现形式，一种由几何元素表示，一种由迹线来表示。

根据平面对投影面的相对位置，分为一般位置平面与特殊位置平面。

本章将讨论各种位置平面的投影特征及平面内的点和直学习基本要求1 熟悉特殊位置平面的投影特征并正确画出其投影。

2 熟练掌握在平面内取点和直线的作图方法。

3 会运用最大斜度线求平面对投影面的倾角。

5.1 平面表示方法—几何元素表示法平面投影在投影图中表示一个平面可以采用两种方式：1.几何元素表示法2.迹线表示法所谓表示平面，主要是表示平面的空间位置，而非其面积大小。

用几何元素表示平面的方法有以下几种方式：平面表示方法—用迹线表示法平面与投影面的交线称为平面的迹线。

当平面位置一定时，则平面的迹线也就唯一确定。

因此，可以用平面的迹线来表示平面在投影体系中的位置。

上面这种用平面迹线表示的平面称为“迹线面”。

平面投影图例5.2.1 一般位置平面与三个投影面均倾斜的平面称为“倾斜面”或“一般位置平面”一般位置平面的三面投影均为该平面图形的类似形。

没有积聚性，也不能反映平面实际形状。

图例5.2.2 特殊位置平面特殊位置平面是指投影面垂直面和投影面平行面。

1.投影面垂直面与一个投影面垂直的平面称为“投影面垂直面”。

在三投影面体系中，投影面垂直面有三种：正垂面、铅垂面、侧垂面。

此处以铅垂面为例分析投影面垂直面的投影特性。

分析可知，铅垂面的投影特性为：a.铅垂面的水平投影积聚为一直线，该直线与投影轴的夹角反映平面与相邻投影面的倾角；b.铅垂面的另两个投影为类似形。

正垂面、铅垂面、侧垂面的投影特征参见表5-1。

铅垂面投影特性各种投影面垂直面的投影特征平面投影图例由表5-1所列正垂面、铅垂面、侧垂面的投影情况可归纳出投影面垂直面的投影特征如下:(1) 投影面垂直面在其所垂直的投影面上的投影积聚为一直线,该直线段与投影轴的夹角反映了该平面与另两个投影面的倾角;(2) 投影面垂直面的另两个投影为类似形。