下载文档原格式
方向导数与梯度公式关系方向导数和梯度是微积分中两个常用的概念,它们之间的关系可以用以下公式表示:方向导数 = 梯度 / 权重其中,梯度是指目标函数对变量的导数,权重是指变量的系数。
具体来说,假设我们有一个线性回归模型$$y = x"beta + epsilon$$其中$y$是输出变量,$x$是输入变量,$beta$是模型的参数,$epsilon$是噪声。
那么,$beta$的梯度可以表示为:$$frac{partial}{partial beta}left(frac{y}{x"beta}ight) = frac{partial y}{partial beta}x" - frac{partial x"}{partial beta}frac{y}{x"beta} = frac{y"beta - x"betay}{x"beta}$$其中,$frac{partial y}{partial beta}$表示$beta$对$y$的导数,$frac{partial x"}{partial beta}$表示$x"beta$对$x$的导数。
现在,如果我们想要计算$beta$的方向导数,可以使用上述公式:$$frac{partial}{partial beta}left(frac{y}{x"beta}ight) = frac{y"beta - x"beta y}{x"beta} = frac{y"}{x"}beta - frac{x"}{x"}beta = frac{y-x"beta"}{x"}$$其中,$beta" = x"(beta)$。
因此,$beta$的方向导数可以通过计算它与其他变量的差来得到。
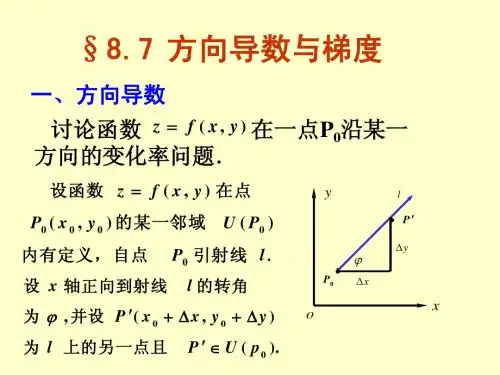
方向导数与梯度的关系与计算公式方向导数（Directional Derivative）是多元函数在某个给定点上沿指定方向的变化率。
它在物理学、工程学和优化问题中具有重要的应用。
在求解方向导数时，我们常常会遇到梯度（Gradient）的概念。
本文将介绍方向导数与梯度之间的关系，并探讨它们的计算公式。
一、方向导数的定义在多元函数中，给定一个点P(x₀, y₀, z₀)及一个单位向量u = (a, b, c)，其中a² + b² + c² = 1，方向导数Duf(x₀, y₀, z₀)表示函数f(x, y, z)在P点上沿u方向的变化率。
方向导数用符号∇f(x₀, y₀, z₀)·u表示。
二、梯度的定义梯度是一个向量，它在多元函数的每个点上都有定义。
对于二元函数f(x, y)，梯度∇f(x, y)表示函数f在每个点上的变化率最大的方向。
梯度可以用向量形式表示为∇f(x, y) = (fx, fy)，其中fx和fy分别表示f对x和y的偏导数。
对于三元函数f(x, y, z)，梯度∇f(x, y, z)表示函数f在每个点上的变化率最大的方向。
梯度可以用向量形式表示为∇f(x, y, z) = (fx, fy, fz)，其中fx、fy和fz分别表示f对x、y和z的偏导数。
三、方向导数与梯度的关系在函数f(x, y, z)的某一点P(x₀, y₀, z₀)处，方向导数和梯度的关系可以表示为：Duf(x₀, y₀, z₀) = ∇f(x₀, y₀, z₀)·u即，方向导数等于梯度与单位向量u的内积。
四、方向导数的计算公式在笛卡尔坐标系中，给定一个点P(x₀, y₀, z₀)及一个非零向量u = (a, b, c)，其中a² + b² + c² = 1，方向导数可以通过以下公式计算：Duf(x₀, y₀, z₀) = fx(x₀, y₀, z₀)a + fy(x₀, y₀, z₀)b + fz(x₀, y₀, z₀)c其中fx、fy和fz分别表示f对x、y和z的偏导数。
