时间序列分析 第三章 平稳时间序列分析

《时间序列分析》课程教学大纲一、课程基本信息二、课程教学目标本课程的目的是使学生掌握时间序列分析的基本理论和方法，让学生借助计算机的存储功能和计算功能来抽象掉其深奥的数学理论和复杂的运算，通过建模练习来掌握时间序列分析的基本思路和方法。

第一，通过这门课程的学习，培养学生对分析方法的理解，使学生初步掌握分析随机数据序列的基本思路和方法。

第二，通过这门课程的学习，使得学生能够运用时间序列分析知识和理论去分析、解决实际问题。

第三，通过这门课程的学习，提高学生利用时间序列的基本思想来处理实际问题，为后续学习打下方法论基础。

三、教学学时分配《时间序列分析》课程理论教学学时分配表《时间序列分析》课程实验内容设置与教学要求一览表四、教学内容和教学要求第一章时间序列分析简介（学时4）（一）教学要求通过本章内容的学习，了解时间序列的定义，理解时间序列的常用分析方法，掌握随机过程、平稳随机过程、非平稳随机过程、自相关基本概念。

（二）教学重点与难点教学重点：时间序列的相关概念。

教学难点：随机过程、系统自相关性。

（三）教学内容第一节引言第二节时间序列的定义（拟采用慕课或翻转课堂）第三节时间序列分析方法1．描述性时序分析2．统计时序分析第四节时间序列分析软件第五节上机指导1．创建时间序列数据集2．时间序列数据集的处理本章习题要点：1、基本概念和特征；2、软件基本操作。

第二章时间序列的预处理（学时6）（拟采用慕课或翻转课堂）（一）教学要求通过本章内容的学习，了解平稳时间序列的定义，理解平稳性和随机性检验的原理，掌握平稳性和随机性检验的方法。

（二）教学重点与难点教学重点：平稳时间序列的定义及统计性质。

教学难点：时间序列的相关统计量。

（三）教学内容第一节平稳性检验1．特征统计量2．平稳时间序列的定义3．平稳时间序列的统计性质4．平稳时间序列的意义5．平稳性的检验第二节纯随机性检验1．纯随机序列的定义2．白噪声序列的性质3．纯随机性的检验第二节上机指导1．绘制时序图2．平稳性与纯随机性检验本章习题要点：1、绘制给定时间序列的相关图；2、计算给定时间序列的相关统计量；3、检验序列的平稳性及纯随机性。

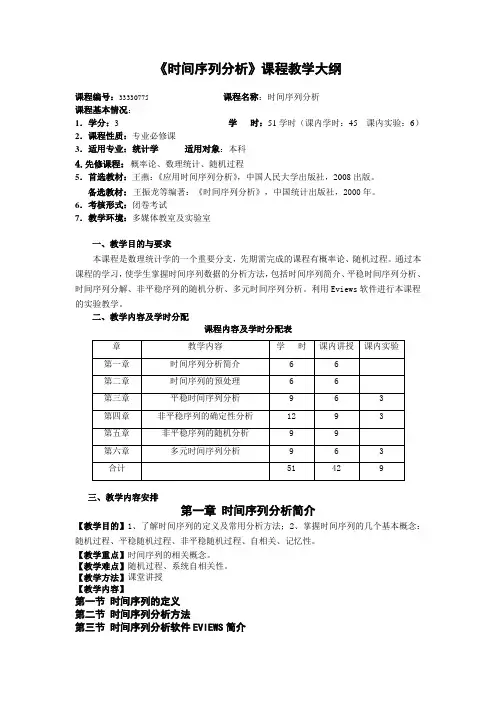
《时间序列分析》课程教学大纲课程编号：33330775课程名称：时间序列分析课程基本情况：1．学分：3 学时：51学时（课内学时：45 课内实验：6）2．课程性质：专业必修课3．适用专业：统计学适用对象：本科4.先修课程：概率论、数理统计、随机过程5．首选教材：王燕：《应用时间序列分析》，中国人民大学出版社，2008出版。

备选教材：王振龙等编著：《时间序列分析》，中国统计出版社，2000年。

6．考核形式：闭卷考试7．教学环境：多媒体教室及实验室一、教学目的与要求本课程是数理统计学的一个重要分支，先期需完成的课程有概率论、随机过程。

通过本课程的学习，使学生掌握时间序列数据的分析方法，包括时间序列简介、平稳时间序列分析、时间序列分解、非平稳序列的随机分析、多元时间序列分析。

利用Eviews软件进行本课程的实验教学。

二、教学内容及学时分配课程内容及学时分配表三、教学内容安排第一章时间序列分析简介【教学目的】1、了解时间序列的定义及常用分析方法；2、掌握时间序列的几个基本概念：随机过程、平稳随机过程、非平稳随机过程、自相关、记忆性。

【教学重点】时间序列的相关概念。

【教学难点】随机过程、系统自相关性。

【教学方法】课堂讲授【教学内容】第一节时间序列的定义第二节时间序列分析方法第三节时间序列分析软件EVIEWS简介第二章时间序列的预处理【教学目的】1、掌握平稳性检验的原理和方法；2、掌握纯随机性检验的原理和方法。

【教学重点】平稳时间序列的定义及统计性质。

【教学难点】时间序列的相关统计量。

【教学方法】课堂讲授【教学内容】第一节平稳性检验一、特征统计量二、平稳时间序列的定义三、平稳时间序列的统计性质四、平稳时间序列的意义五、平稳时间序列的检验第二节纯随机性检验一、纯随机序列的定义二、白噪声序列的定义三、纯随机性检验第三章平稳时间序列序列分析【教学目的】1、理解ARMA模型的定义及性质。

2、掌握平稳序列建模方法。

3、掌握平稳时间序列的预测【教学重点】平稳时间序列建模【教学难点】模型识别，参数估计，序列预测【教学方法】课堂讲授与上机实验【教学内容】第一节方法性工具一、差分运算二、延迟算子三、线性差分方程第二节 ARMA模型的性质一、AR模型二、MA模型三、ARMA模型第三节平稳序列建模一、建模步骤二、样本自相关系数与偏相关系数三、模型识别四、参数估计五、模型检验六、模型优化第四节序列预测一、线性预测函数二、预测方差最小原则三、线性最小方差预测的性质四、修正预测第四章非平稳序列的确定性分析【教学目的】1、理解时间序列的分解原理。

注：图中，S号代表序列的观察值；连续曲线代表拟合序列曲线；虚线代表拟合序列的95%上下置信限。

所谓预测就是要利用序列以观察到的样本值对序列在未来某个时刻的取值进行估计。

目前对平稳序列最常用的预测方法是线性最小方差预测。

线性是指预测值为观察值序列的线性函数，最小方差是指预测方差达到最小。

在预测图上可以看到，数据围绕一个范围内波动，即说明未来的数值变化时平稳的。

二、课后习题第十七题：根据某城市过去63年中每年降雪量数据（单位：mm）得：（书本P94）程序：data example17_1;input x@@;time=_n_;cards;2579588397 110;proc gplot data=example17_1;plot x*time=1;symbol c=red i=join v=star;run;proc arima data=example17_1;identify var=x nlag=15minic p= (0:5) q=(0:5);run;estimate p=1;run;estimate p=1 noin;run;forecast lead=5id=time out=results;run;proc gplot data=results;plot x*time=1 forecast*time=2 l95*time=3 u95*time=3/overlay;symbol1c=black i=none v=start;symbol2c=red i=join v=none;symbol3c=green i=join v=none l=32;run;（1）判断该序列的平稳性与纯随机性该序列的时序图如下（图a）图a由时序图显示过去63年中每年降雪量数据围绕早70mm附近随机波动，没有明显趋势或周期，基本可以看成平稳序列，为了稳妥起见，做了如下自相关图（图b）图b时序图就是一个平面二维坐标图，通常横轴表示时间，纵轴表示序列取值。

《时间序列分析——基于R》王燕，读书笔记笔记：⼀、检验：1、平稳性检验：图检验⽅法：时序图检验：该序列有明显的趋势性或周期性，则不是平稳序列⾃相关图检验：（acf函数）平稳序列具有短期相关性，即随着延迟期数k的增加，平稳序列的⾃相关系数ρ会很快地衰减向0（指数级指数级衰减），反之⾮平稳序列衰减速度会⽐较慢衰减构造检验统计量进⾏假设检验：单位根检验adfTest()——fUnitRoots包2、纯随机性检验、⽩噪声检验（Box.test（data，type，lag=n）——lag表⽰输出滞后n阶的⽩噪声检验统计量，默认为滞后1阶的检验统计量结果）1、Q统计量：type=“Box-Pierce”2、LB统计量：type=“Ljung-Box”⼆、模型1、ARMA平稳序列模型1.1平稳性检验1.2ARMA的p、q定阶——acf（），pacf（），auto.arima（）⾃动定阶1.3建模arima()1.4模型显著性检验：残差的⽩噪声检验Box.test（）；参数显著性检验t分布2、⾮平稳确定性分析2.1趋势拟合：直线、曲线（⼀般是多项式，还有其它函数）2.2平滑法移动平均法：SMA()——TTR包指数平滑法：HoltWinters()3、⾮平稳随机性分析3.1ARIMA1平稳性检验，差分运算2拟合ARMA3⽩噪声检验3.2疏系数模型arima（p,d,f）3.3季节模型可以叠加的模型4、残差⾃回归模型：4.1建⽴线性模型4.2对滞后的因变量间拟合线性模型，对模型做残差⾃相关DW检验。

dwtest()——lmtest包，增加选项order.by指定延迟因变量4.3对残差建⽴ARIMA模型5、条件异⽅差模型：异⽅差检验：LM检验ArchTest（）——FinTS包，⽤ARCH、GARCH模型建模第⼀章简介统计时序分析⽅法：1、频域分析⽅法2、时域分析⽅法步骤：1、观察序列特征2、根据序列特征选择模型3、确定模型的⼝径4、检验模型，优化模型5、推断序列其它统计性质或预测序列将来的发展时域分析研究的发展⽅向：1、AR，MA，ARMA，ARIMA（Box-Jenkins模型）2、异⽅差场合：ARCH，GARCH等（计量经济学）3、多变量场合：“变量是平稳”不再是必需条件，协整理论3、⾮线性场合：门限⾃回归模型，马尔科夫转移模型第⼆章时间序列的预处理预处理内容：对它的平稳性和纯随机性进⾏检验，最好是平稳⾮⽩噪声的序列1、特征统计量1.1概率分布分布函数或密度函数能够完整地描述⼀个随机变量的统计特征，同样⼀个随机变量族{Xt}的统计特性也完全由它们的联合分布函数或联合密度函数决定。

时间序列分析中的平稳性与非平稳性时间序列分析是一种用来研究时间数据的统计方法，它可以揭示出时间序列数据的模式和趋势，并预测未来的发展。

在进行时间序列分析时，我们经常会遇到平稳性和非平稳性的问题，本文将重点讨论这两个概念及其在时间序列分析中的重要性。

1. 什么是平稳性？平稳性是指时间序列在统计特性上具有不变性，即其均值和方差不随时间的推移而发生改变。

具体而言，平稳时间序列的均值在时间维度上是稳定的，方差也不会随时间变化而增加或减小。

此外，平稳时间序列的自协方差只与时间间隔有关，而与特定时间点无关。

2. 平稳性的判断方法为了判断一个时间序列是否具有平稳性，我们可以使用一些统计检验方法。

常见的方法有ADF检验（Augmented Dickey-Fuller test）、KPSS检验（Kwiatkowski-Phillips-Schmidt-Shin test）等。

ADF检验通常用于检验平稳性，其原假设是时间序列具有单位根（非平稳），如果检验结果拒绝了原假设，则可以得出时间序列是平稳的结论。

3. 非平稳性的表现形式非平稳性的时间序列可能会呈现出明显的趋势、季节性或周期性变化。

趋势是时间序列长期的、持续的上升或下降，季节性是指时间序列在特定时间点上出现的周期性波动，周期性是指时间序列存在长期的、不规则的上升或下降。

4. 非平稳性的处理方法如果时间序列是非平稳的，我们需要对其进行处理，以使其具备平稳性。

常见的处理方法有差分法、对数变换等。

差分法可以通过计算相邻时间点的差值来消除趋势和季节性，对数变换则可以通过对时间序列取对数来减少其波动性。

5. 平稳性的重要性平稳性在时间序列分析中非常重要，具有以下几个方面的意义： - 简化模型：平稳时间序列的统计特性稳定，可以简化模型的建立和预测。

- 降低误差：平稳时间序列的随机误差具有恒定的方差，使得模型的预测更准确。

- 提高可靠性：基于平稳时间序列建立的模型具有更好的可靠性和稳定性，可以更好地应对未来的变化。

第3章平稳时间序列分析本章教学内容与要求：了解时间序列分析的方法性工具；理解并掌握ARMA 模型的性质；掌握时间序列建模的方法步骤及预测；能够利用软件进行模型的识别、参数的估计以及序列的建模与预测。

本章教学重点与难点：利用软件进行模型的识别、参数的估计以及序列的建模与预测。

型来息。

t x 为t x 的1阶差分： ▽1t t t x x x --=对1阶差分后的序列再进行一次1阶差分运算称为2阶差分，记▽2tx 为t x 的2阶差分：▽2t x =▽t x -▽1-t x以此类推，对p-1阶差分厚序列再进行一次1阶差分运算称为p 阶差分。

记▽p t x 为t x 的p 阶差分：▽p t x =▽p-1t x -▽p-11-t x （二）k 步差分kt x 为t x 的10,,1t = 10,,2 = 即2阶差分序列▽2t x ：3，22，-63，-54，-6，16，-52，-40，10,,3t = 2步差分：▽29x x x 133=-= ▽234x x x 244=-=……▽2-28x x x 81010=-=即2步差分序列：9，34，-7，-26，12，21，-16，-28 二、延迟算子（滞后算子） （一）定义延迟算子类似于一个时间指针，当前序列值乘以一个延迟算子，就相x因此，15-18+6=343-30+9=222.k 步差分▽k =t k t k t k t t x )B 1(x B x x x -=-=--三、线性差分方程在实践序列的时域分析中，线性差分方程是非常重要的，也是极为有效的工具，事实上，任何一个ARMA模型都是一个现象差分方程。

因此，ARMA模型的性质往往取决于差分方程的性质。

为了更好地讨论ARMA 模型的性质，先简单介绍差分方程的一般性质。

设,，方程两边同除以，得特征方程（这是一个一元p次方程，应该至少有p个非零实根，称这p个实根为特征方程（3）的特征根，不防记作.特征根的取值情况不同，齐次线性差分方程的解会有不同的表达形式。

t Pp t tt t t x B x x B x Bxx ===---221第3章第三章平稳时间序列分析一个序列通过预处理被识别为平稳非白噪声序列，那就说明该序列是一个蕴含着有关信息的平稳序列。

3.1 方法性工具 3.1.1 差分运算 一、p 阶差分记t x ∇为t x 的1阶差分：1--=∇t t t x x x记t x 2∇为t x 的2阶差分：21122---+-=∇-∇=∇t t t t t t x x x x x x以此类推：记t p x ∇为t x 的p 阶差分：111---∇-∇=∇t p t p t p x x x 二、k 步差分记t k x ∇为t x 的k 步差分：k t t t k x x x --=∇3.1.2 延迟算子 一、定义延迟算子相当与一个时间指针，当前序列值乘以一个延迟算子，就相当于把当前序列值的时间向过去拨了一个时刻。

记B 为延迟算子，有延迟算子的性质：1.10=B2.若c 为任一常数，有1)()(-⋅=⋅=⋅t t t x c x B c x c B3.对任意俩个序列{t x }与{t y }，有11)(--±=±t t t t y x y x B4.n t t n x x B -=5.)!(!!,)1()1(0i n i n C B C B i n i i n ni i n-=-=-∑=其中二、用延迟算子表示差分运算 1、p 阶差分t p t p x B x )1(-=∇ 2、k 步差分t k k t t t k x B x x x )1(-=-=∇-3.2 ARMA 模型的性质 3.2.1 AR 模型定义 具有如下结构的模型称之p 阶自回归模型，简记为AR(p):ts Ex t s E Var E x x x x t s t s t t p tp t p t t t ∀=≠===≠+++++=---,0,0)(,)(,0)(,0222110εεεσεεφεφφφφε (3.4)AR(p)模型有三个限制条件：条件一：0≠p φ。

第三章 平稳ARMA 过程一元ARMA 模型是描述时间序列动态性质的基本模型。

通过介绍ARMA 模型，可以了解一些重要的时间序列的基本概念，并且为描述单变量时间序列的动态性质提供一类十分有用的模型。

§3.1 预期、平稳性和遍历性3.1.1 预期和随机过程假设可以观察到一个样本容量为T 的随机变量t Y 的样本：},,,{21T y y y这意味着这些随机变量之间的是相互独立且同分布的。

例3.1 假设T 个随机变量的集合为：},,,{21T εεε ，),0(~2σεN i 且相互独立，我们称其为高斯白噪声过程产生的样本。

对于一个随机变量t Y 而言，它是t 时刻的随机变量，因此即使在t 时刻实验，它也可以具有不同的取值，假设进行多次试验，其方式可能是进行多次整个时间序列的试验，获得I 个时间序列：+∞=-∞=t t t y }{)1(，+∞=-∞=t t t y }{)2(，…，+∞=-∞=t t I t y }{)(将其中仅仅是t 时刻的观测值抽取出来，得到序列：},,,{)()2()1(I t t t y y y ，这个序列便是对随机变量t Y 在t 时刻的I 次观测值，也是一种简单随机子样。

定义3.1 假设随机变量t Y 是定义在相同概率空间},,{P ℜΩ上的随机变量，则称随机变量集合},2,1,0,{ ±±=t Y t 为随机过程。

例3.2 假设随机变量t Y 的概率密度函数为：]21exp[21)(22t t Y y y f t σσπ= 此时称此时密度为该过程的无条件密度，此过程也称为高斯过程或者正态过程。

定义3.2 可以利用各阶矩描述随机过程的数值特征：(1) 随机变量t Y 的数学期望定义为(假设积分收敛)：⎰==+∞∞-tt Y t t t dy y f y Y E t )()(μ (3.1) 此时它是随机样本的概率极限：∑==∞→I i i t I t y I P Y E 1)(1lim)( (3.2) (2) 随机变量t Y 的方差定义为(假设积分收敛): 20)(t t t Y E μγ-= (3.3) 例3.3 几种重要类型的随机过程1) 假设},,{21 εε是一个高斯白噪声过程，随机过程t Y 为常数加上高斯白噪声过程：t t Y εμ+=则它的均值和方差分别为：μεμμ=+==)()(t t t E Y E2220)()(σεμγ==-=t t t t E Y E(2) 随机过程t Y 为时间的线性趋势加上高斯白噪声过程：t t t Y εβ+=则它的均值和方差分别为：t E t Y E t t t βεβμ=+==)()(2220)()(σεμγ==-=t t t t E Y E3.1.2 随机过程的自协方差函数将j 个时间间隔的随机变量构成一个随机向量),,,(1'=--j t t t t Y Y Y X ，通过随机试验可以获得该随机向量的简单随机样本。

时间序列分析——基于R 王燕答案第一章时间序列分析简介略第二章时间序列的预处理#========================================## 2.5习题-1##========================================library(tseries)par(mfrow=c(1,2))x=rep(1:20)temp=ts(x)plot(temp)#不是平稳序列as.vector(acf(temp)$acf[1:6])#序列的自相关系数递减到零的速度相当缓慢，#在很长的延迟时期里，自相关系数一直为正，#而后又一直为负，在自相关图上显示出明显的#三角对称性，这是具有单调趋势的非平稳序列#的一种典型的自相关图形式。

这和该序列时序#图显示的显著的单调递增性是一致的。

#======================================== ## 2.5习题-2##======================================== library(tseries)par(mfrow=c(1,2))volcano.co2=read.table('习题2.2数据.txt',sep='\t',header=F) data=ts(as.vector(t(as.matrix(volcano.co2))),start=c(1975,1)) plot(data)#不是平稳序列as.vector(acf(data,lag.max=23)$acf)#序列自相关系数长期位于零轴的一边。

这是#具有单调趋势序列的典型特征，同时自相关#图呈现出明显的正弦波动规律，这是具有周#期变化规律的非平稳序列的典型特征。

自相#关图显示出来的这两个性质和该序列时序图#显示出的带长期递增趋势的周期性质是非常#吻合的。

#========================================## 2.5习题-3##======================================== library(tseries)par(mfrow=c(1,2))rain=read.table('习题2.3数据.txt',sep='\t',header=F) data=ts(as.vector(t(as.matrix(rain))),start=c(1945,1)) plot(data)#该序列为平稳序列as.vector(acf(data,lag.max = 23)$acf)#该序列的自相关系数一直都比较小，#基本控制在2倍的标准差范闹以内，#可以认为该序列自始至终都在零轴附#近波动，这是随机性非常强的平稳时#间序列通常具有的自相关图特征。

时间序列分析中的平稳性检验时间序列分析是统计学中重要的研究领域，它用于研究随时间变化的数据，并预测未来的趋势。

平稳性检验是时间序列分析的关键步骤之一，它用于确定时间序列数据是否具有平稳性。

本文将介绍时间序列分析中的平稳性检验的基本概念、方法和应用。

一、平稳性的概念在时间序列分析中，平稳性是指时间序列数据的统计特性在不同时间段内保持不变。

具体而言，平稳性要求时间序列的均值、方差和自相关函数在时间上不发生显著的变化。

如果时间序列数据具有平稳性，那么我们可以利用历史数据对未来进行可靠的预测。

二、平稳性检验的方法为了检验时间序列数据的平稳性，常用的方法包括观察法、单位根检验和ADF检验。

1. 观察法观察法是最简单的平稳性检验方法，它通过观察时间序列数据的图表和统计指标来判断数据是否具有平稳性。

如果时间序列数据的均值和方差在不同时间段内保持相对稳定，且自相关函数衰减较快，那么可以初步认为数据具有平稳性。

2. 单位根检验单位根检验是一种常用的平稳性检验方法，它基于时间序列数据是否具有单位根来判断数据的平稳性。

常用的单位根检验方法包括ADF检验、PP检验和KPSS 检验。

其中，ADF检验是最常用的单位根检验方法之一。

3. ADF检验ADF检验（Augmented Dickey-Fuller test）是一种常用的单位根检验方法，它基于Dickey-Fuller回归模型来判断时间序列数据是否具有单位根。

ADF检验的原假设是时间序列数据具有单位根，即非平稳性；备择假设是时间序列数据不具有单位根，即平稳性。

ADF检验的关键统计量是ADF统计量，它的值与临界值进行比较来判断数据的平稳性。

如果ADF统计量的值小于临界值，那么可以拒绝原假设，认为数据具有平稳性；如果ADF统计量的值大于临界值，那么接受原假设，认为数据不具有平稳性。

三、平稳性检验的应用平稳性检验在时间序列分析中具有广泛的应用。

首先，平稳性检验是进行时间序列建模的前提条件，只有具有平稳性的数据才能进行可靠的建模和预测。

时间序列分析第三章平稳时间序列分析轴表示序列取值。

时序图可以直观地帮助我们掌握时间序列的一些基本分布特征。

根据平稳时间序列均值、方差为常数的性质，平稳序列的时序图应该显示出该序列始终在一个常数值附近随机波动，而且波动的范围有界的特点。

如果观察序列的时序图，显示出该序列有明显的趋势性或周期性，那它通常不是平稳序列。

从图上可以看出，数值围绕在0附近随机波动，没有明显或周期，其本可以视为平稳序列，时序图显示该序列波动平稳。

procarimadata=e某ample3_1;identifyvar=某nlag=8;run;图一图二样本自相关图图三样本逆自相关图2图四样本偏自相关图图五纯随机检验图实验结果分析：（1）由图一我们可以知道序列样本的序列均值为-0.06595，标准差为1.561613，观察值个数为84个。

（2）根据图二序列样本的自相关图我们可以知道该图横轴表示自相关系数，综轴表示延迟时期数，用水平方向的垂线表示自相关系数的大小。

我们发现样本自相关图延迟3阶之后，自相关系数都落入2倍标准差范围以内，而且自相关系数向0.03衰减的速度非常快，延迟5阶之后自相关系数即在0.03值附近波动。

这是一个短期相关的样本自相关图。

所以根据样本自相关图的相关性质，可以认为该序列平稳。

（3）根据图五的检验结果我们知道，在各阶延迟下LB检验统计量的P值都非常小（<0.0001），所以我们可以以很大的把握（置信水平>99.999%）断定该序列样本属于非白噪声序列。

procarimadata=e某ample3_1;identifyvar=某nlag=8minicp=(0:5)q=(0:5);run;IDENTIFY命令输出的最小信息量结果3某个观察值序列通过序列预处理，可以判定为平稳非白噪声序列，就可以利用ARMA模型对该序列建模。

建模的基本步骤如下：A：求出该观察值序列的样本自相关系数（ACF）和样本偏自相关系数（PACF）的值。