下载文档原格式
2017江苏南京航空航天大学理论力学考研真题第 1 题（25 分）图示平面结构，由直角折杆 ABC 和直角折杆CDE 组成，C 为光滑铰链，A 处为固定端，E 处为可动铰支座。
BC 和 CD 段上作用载荷集度 q的均布力，杆 ABC 上作用力偶矩为 M=qa2 的力偶，杆 AB 的中点处作用一大小为 qa 的力 F，结构尺寸如图所示，BC=CD=DE=a，AB=2a，其中载荷集度 q，长度 a 为已知量，不计各杆自重及各处摩擦。
求 E 处和 A 处的约束力。
第 2 题（15 分）已知：正方体的边长为 a，轴 AB 与水平面夹角为30 ，力 F 作用如图所示。
建立直角坐标系 Oxyz 如图。
试求：（1）力 F 对 x 轴、y 轴的矩 Mx（F）、My（F）；（2）力 F 对 AB 轴（方向从点 A 指向点 B）的矩（F）。
第 3 题（20 分）图示平面机构，半径为 R 的圆轮，以匀角速度ω绕轴 O 顺时针转动，并带动杆 AB 绕轴 A 转动。
在图示瞬时，OC 与铅垂线的夹角为，杆 AB 水平，圆轮与杆 AB 的接触点 D 距A 为。
试用点的复合运动方法求：此时杆 AB 的角速度和角加速度。
第 4 题（25 分）图示平面四连杆机构，已知：AB = BC = l=1m，CD = 2l。
在图示瞬时 A、B、C 三点成一直线，且杆CD 与水平线 AD 夹角为，杆 AB 的角速度为=3rad/s，角加速度为零。
求该瞬时杆 CD 的角速度和角加速度。
第 5 题（20 分）均质细杆 OA 可绕垂直纸面的水平轴 O 转动，另一端A 与均质细杆 BD 的中点铰接，杆 BD 可绕铰 A 在铅垂面内自由旋转，如图所示。
已知两杆长均为 l，质量均为 m，各处摩擦不计。
初始时杆 BD 铅垂，θ= 30°，两杆静止。
试：（1）写出杆 OA 运动到任意位置时杆 OA 和杆 BD 的动能；（2）求杆 OA 运动到铅垂位置时两杆的角速度。
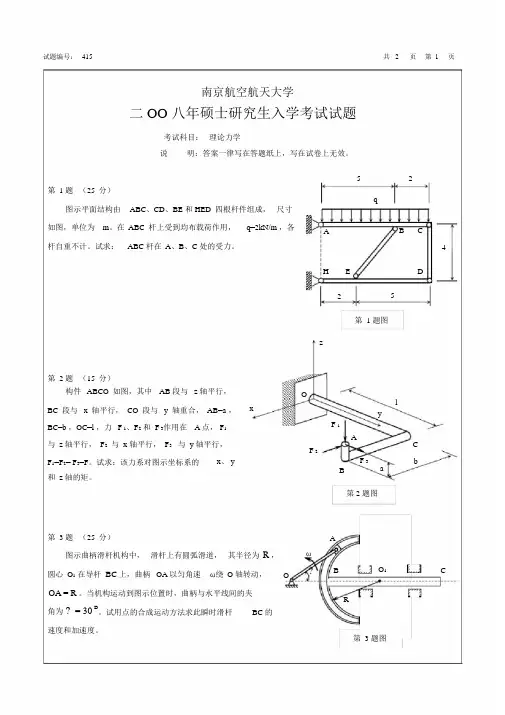
2007年南京航天航空大学硕士入学考试试题考试科目：材料力学1、如图所示，三根绳索悬挂一块刚性板。
A和B处用铝绳，铝绳直径3mm，弹性模量72GPa，许用应力96MPa；C处用钢绳，钢绳直径2mm，弹性模量200GPa，许用应力124MPa。
求最大载荷P。
（15分）（答案：P max＝705N）题1图2、如图所示，电机匀速转动时，施加800Nm的扭矩在等截面圆钢轴ABCD上。
已知A 和D间的最大允许扭转角为1.5°，剪切弹性模量G＝77GPa，许用切应力[η]＝60MPa。
试求轴的最小直径。
（15分）（答案：d min＝42.1mm）题2图3、试作图示梁的剪力图和弯矩图。
（15分）题3图4、矩形截面外伸梁作用均布载荷q，BC段梁的尺寸为：高度h＝90mm，宽度b＝40mm，AB梁段尺寸为：高度h＝70mm，宽度b＝30mm，材料的许用应力[ζ]＝200MPa，试求许可均布载荷q。
（15分）题4图5、小型密封容器除承受内压p外，在两端还承受轴向压力F p。
若容器平均直径为D；壁厚为δ。
且F p＝2pDπδ。
P、D、、δ等均已知，且D＝2πδ。
试：（1）、用单元体表示危险点的应力状态；（2）、确定危险点的三个主应力；（3）、确定危险点的最大剪应力。
（15分）（答案：ζ1＝10p, ζ2＝3p, ζ3＝－p, ηmax＝5.5p）题5图6、构件一点的应力状态如图所示，若ζx＝－100MPa，ζy＝100MPa，ηxy＝100MPa，材料的许用应力[ζ]＝300MPa。
计算点的主应力，并用第三强度理论对其进行强度校核。
（15分）（答案：ζ1＝ζmax＝141MPa, ζ2＝0, ζ3＝－141MPa, ζ1－ζ3＝282MPa≤[ζ]＝300MPa）7、某主轴受轴向拉伸与扭转联合作用，为了用实验方法测定拉力F p及外力偶M e，在主轴上沿轴线方向及与轴向45°夹角方向各贴一枚电阻应变片，今测得轴在等速旋转时轴向应变平均值与45°方向应变平均值分别为ε0°＝500×10－6，ε45°＝80×10－6。
第十四章达朗贝尔原理1．平移刚体上的惯性力系向任意点简化，所得主矢相同，R Q ＝－m a C 。
设质心为C ，点O 到质心的矢径为r C ，则惯性力系向O 点简化的主矩为（ ）。
① ＭQO ＝0② ＭQO ＝J O α③ ＭQO ＝J C α④ ＭQO ＝r C ×R Q正确答案：④2．定轴转动刚体，其转轴垂直于质量对称平面，且不通过质心C ，当角速度ω＝0，角加速度α≠0时，其惯性力系的合力大小为R Q ＝ma C ，合力作用线的方位是（ ）。
（设转轴中心O 与质心C 的连线为OC ；J C 、J O 分别为刚体对质心及转轴中心的转动惯量）。
① 合力作用线通过转轴轴心，且垂直于OC② 合力作用线通过质心，且垂直于OC③ 合力作用线至轴心的垂直距离为h ＝J O α / ma C④ 合力作用线至轴心的垂直距离为h ＝OC ＋J C α / ma C正确答案：③、④3．刚体作定轴转动时，附加动反力等于零的充分必要条件是（ ）。
① 转轴是惯性主轴② 质心位于转轴上③ 转轴与质量对称面垂直④ 转轴是中心惯性主轴正确答案：④4．如图所示，质量为m 的质点A ，相对于半径为r 的圆环作匀速圆周运动，速度为u ；圆环绕O 轴转动，在图示瞬时角速度为ω，角加速度为α。
则图示瞬时，质点A 的惯性力为（ ）。
① )22(ωαu r m F gx +=)/2(22r u r m F gy +=ω② )22(ωαu r m F gx +−=)/2(22r u r m F gy +−=ω③ αmr F gx 2−=)22/(22ωωr u r u m F gy +−=④ 0=gx Fr mu F gy /2−=正确答案：③5．如图所示，半径为r ，质量为m 的均质圆盘与质量也为m 、长为l 的均质杆焊在一起，并绕O轴转动。
在图示瞬时，角速度为ω，角加速度为α 。
则惯性力系向O 点简化结果为（ ）。
① 2/)23(αm r l F g τ+=2/)23(2ωm r l F gn +=6/)1298(22αm lr r l M gO ++=② 2/)(αm r l F g τ+=2/)(2ωm r l F gn +=6/)1298(22αm lr r l M gO ++=③ 2/)23(αm r l F g τ+=2/)23(2ωm r l F gn +=2/)23(2αm r l M gO +=④ 2/)23(αm r l F g τ+=2/)23(2ωm r l F gn +=4/])(4[22αm r l l M gO ++=正确答案：①6．长度为r 的杆OA 与质量为m 、长度为2r 的均质杆AB 在A 端垂直固接，可绕轴O 转动。
第七章刚体的简单运动1．刚体作平动时，刚体内各点的轨迹（）。
①一定是直线②一定是曲线③可以是直线，也可以是曲线④可以是直线，也可以是不同半径的圆正确答案：③2．某瞬时，刚体上任意两点A、B的速度分别为v A、v B，则下述结论正确的是（）。
①当v A = v B时，刚体必平动②当刚体作平动时，必有|v A| = |v B|，但v A与v B的方向有可能不同③当刚体作平动时，必有v A = v B④当刚体作平动时，v A与v B的方向必然相同，但可能|v A| ≠|v B|正确答案：③3．一对外啮合或内啮合的定轴传动齿轮，若啮合处不打滑，则任一瞬时两轮啮合点处的速度和加速度所满足的关系为（）。
①速度矢量和加速度矢量均相等②速度大小与加速度大小均相等③速度矢量和加速度矢量均不相等④速度矢量和切向加速度矢量均相等正确答案：④4．如图所示的平面机构中，三角板ABC与杆O1A、O2B铰接，若O1A = O2B = r，O2O1 = AB，则顶点C的运动轨迹为（）。
①以CO1长为半径，以O1点为圆心的圆②以CH长为半径，以H点为圆心的圆③以CD长（CD // AO1）为半径，以D点为圆心的圆④以CO = r长（CO // AO1）为半径，以O点为圆心的圆正确答案：④5．刚体绕定轴转动，（）。
①当转角ϕ>0时，角速度ω为正②当角速度ω>0时，角加速度α为正③当ω与α同号时为加速转动，当ω与α异号时为减速转动④当α>0时为加速转动，当α<0时为减速转动正确答案：③6．汽车左转弯时，已知车身作定轴转动，汽车左前灯A的速度大小为v A，汽车右前灯B的速度大小为v B。
A、B之间的距离为b，则汽车定轴转动的角速度大小为（）。
① b v A ② b v B ③ b v v B A )(+ ④ bv v B A )(− 正确答案：④7．每段长度相等的直角折杆在图示的平面内绕O 轴转动，角速度ω为顺时针转向，则M 点的速度方向如图中的（ ）所示。
可编辑修改精选全文完整版07年评分标准及参考答案一（本大题 12 分）总分： 12 分。
(1) 6 分； (2)2 分 ;(3)4 分(1) 滚子B 、 C 两处存在局部自由度，应消除。
(2) 故机构自由度(3)二、（ 14 分）答案：总分 14 分。
(1)4 分； (2)3 分； (3)3 分； (4)4 分图解过程如图所示。
三、（ 16 分）答案总分 16 分 (1) 3 分 (2) 3 分 (3) 3 分 (4) 4 分 (5) 3 分(1) 因用于雷达天线俯仰传动，不应有急回作用 , 故（ 3 分）(2) 作，且使mm （ 3 分）(3) 以D 为圆心，mm 为半径作弧与C 2 C 1 连线的延长线交于A 点。
（ 3 分）(4) 量得mm , mm ,故mm , mm （ 4 分）(5) 作出可能为最小传动角的两个位置，可见在曲柄与机架重叠时，传动角为最小，且量得，满足要求。
〔 3 分〕四、 ( 本大题 16 分 )总分 16 分。
(1)8 分； (2)8 分（ 1 ）求，m/s，作速度多边形，利用影像法求d ，m/s（ 2 ）求，m/s 2，又，m/s 2作加速度多边形，利用影像法求m/s 2 ，方向如图所示五、（本大题 18 分）总分 18 分。
(1) mm（ 3 分）（ 2 分）(2)( 取)(4 分 )(3)（ 5 分）(4) mm(4 分 )六（本题 16 分）答案：答案：总分 16 分(1)，（ 6 分）(2) （ 6 分）(3) r/min （ˉ）（ 2 分）七题、（本题共 8 分）总分： 8 分。
(1) 2 分 (2) 2 分 (3) 2 分 (4)2 分（ 1 ）求N × m（ 2 ）计算各点的盈亏功，画出图。
J（ 3 ）在处，在处。
（ 4 〕。
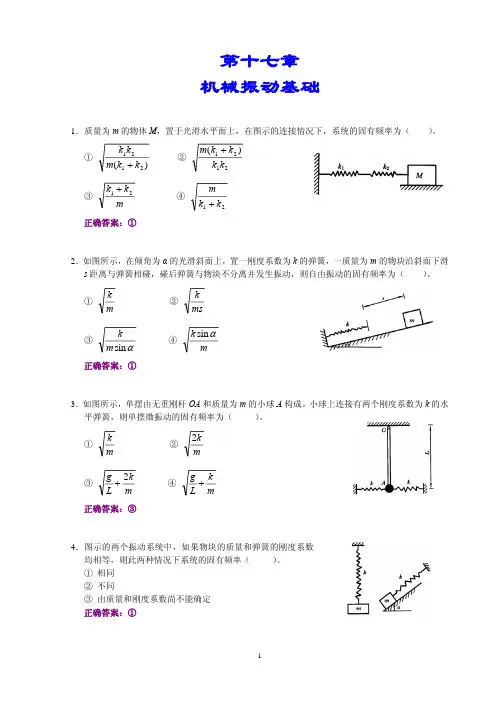
第十七章机械振动基础1．质量为m 的物体M ，置于光滑水平面上，在图示的连接情况下，系统的固有频率为（ ）。
① )(2121k k m k k + ② 2121)(k k k k m + ③m k k 21+ ④ 21k k m + 正确答案：①2．如图所示，在倾角为α的光滑斜面上，置一刚度系数为k 的弹簧，一质量为m 的物块沿斜面下滑s 距离与弹簧相碰，碰后弹簧与物块不分离并发生振动，则自由振动的固有频率为（ ）。
① mk ② ms k ③αsin m k ④ m k αsin 正确答案：①3．如图所示，单摆由无重刚杆OA 和质量为m 的小球A 构成。
小球上连接有两个刚度系数为k 的水平弹簧，则单摆微振动的固有频率为（ ）。
① mk ② m k 2 ③m k L g 2+ ④ m k L g + 正确答案：③4．图示的两个振动系统中，如果物块的质量和弹簧的刚度系数均相等，则此两种情况下系统的固有频率（ ）。
① 相同② 不同③ 由质量和刚度系数尚不能确定正确答案：①5．图示质量弹簧系统，已知物块的质量为m ，弹簧的刚度系数为k ，静伸长为δs ，原长是l 0 。
若以弹簧未伸长的下端点为坐标原点O ，则物块的运动微分方程为（ ）。
① 0=+x mk x ② 0)(=−+s x mk x δ ③ g x mk x s =−+)(δ ④ 0)(=++s x mk x δ 正确答案：②6．在图示中，当把弹簧原长的中点O 固定后，系统的固有频率与原来固有频率的比值为（ ）。
① 21 ② 2③ 2④ 4正确答案：③7．图示弹簧秤，秤盘重未知，当盘上放一重P 的物体时，测得振动周期为T 1；换一重Q 的物体时，其振动周期为T 2，则弹簧的刚度系数应为k =（ ）。
正确答案：)()(421222T T g P Q −−π8．图示为四根弹簧连接而成的振动装置，弹簧的刚度系数分别为k 1和k 2。
假设质量为m 的物块A 沿倾角为α的斜面作平动，则该振动装置的固有频率ω =（ ）。
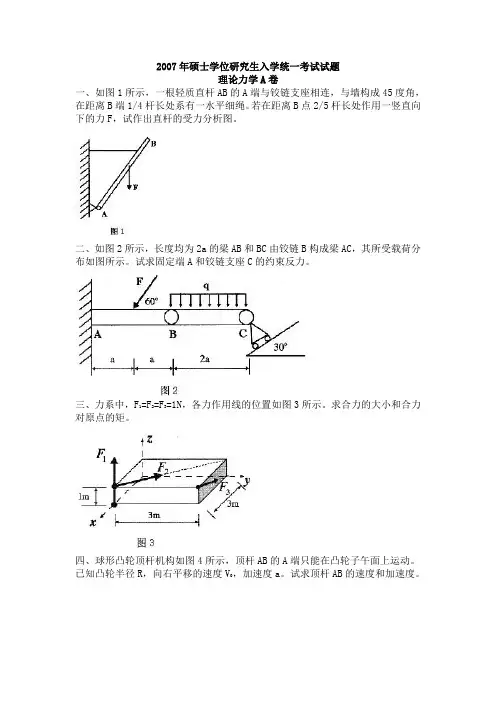
2007年硕士学位研究生入学统一考试试题理论力学A卷一、如图1所示，一根轻质直杆AB的A端与铰链支座相连，与墙构成45度角，在距离B端1/4杆长处系有一水平细绳。
若在距离B点2/5杆长处作用一竖直向下的力F，试作出直杆的受力分析图。
二、如图2所示，长度均为2a的梁AB和BC由铰链B构成梁AC，其所受载荷分布如图所示。
试求固定端A和铰链支座C的约束反力。
三、力系中，F1=F2=F3=1N，各力作用线的位置如图3所示。
求合力的大小和合力对原点的矩。
四、球形凸轮顶杆机构如图4所示，顶杆AB的A端只能在凸轮子午面上运动。
已知凸轮半径R，向右平移的速度V，加速度a。
试求顶杆AB的速度和加速度。
五、如图5所示，一质量为m的物体放在匀速转动的水平转台上，它与转轴的距离为r。
设物体与转台表面的摩擦系数为μ。
当物体不致因转台旋转而滑出时，求水平台的最大转速是多少。
六、图6所示，水平面上放有一质量为M1的均质直三棱柱，在其斜面上又放一质量为M2的均质直三棱柱，质量比为M1:M2=3，两者的尺寸在图中已标注。
设所有摩擦均可忽略，初始时系统静止。
当斜面上的三棱柱下滑到水平面时，质量为M1的三棱柱移动了多少距离。
七、送料机构小车连同矿石的质量为m1，绞轮质量为m2，半径为r，对其转轴的回转半径为r2，轨道的倾角为θ，如图7所示。
在绞轮上作用一不变力矩M将小车提升。
试求小车由静止开始沿轨道上升路程为s时的速度及加速度。
略去摩擦作用及绳索的质量。
八、如图8所示，轮A和B可视为均质圆盘，半径均为r，质量均为m。
绕在二1，并且放在理想光滑的水平面轮上的绳索中间连有物块C，设物块C的质量为m2上。
今在轮B上作用一个不变的力偶M，求轮B与物块C之间那段绳索的张力。
九、均质直杆重为G，长为L，A端为球铰链连接，B端自由，以匀角速度Ω绕铅垂轴AZ转动，如图9所示。
求杆在A端受到铰链的约束力大小。
(应用达朗贝尔原理)图 92007年理论力学A卷参考答案一、答：二、答：1取BC为研究对象进行受力分析，设Nc为C端受到的作用力大小，方cos 30°·2a-2aq·a=0，求得向垂直于斜坡，列出对B点取距的平衡方程Nc。
2010年南京航空航天大学815理论力学考研试题理论力学考研试题（（回忆版回忆版））
常规的7道大题：
1.平面任意力系，求一固定铰支座和一滑动铰支的约束力。
需取隔离体，列矩方程，求出滑动铰支的约束力。
再取整体，列一矩式。
2.空间任意力系。
求一力在各坐标轴的投影及对各坐标轴的矩。
3.点的合成运动。
机构为一偏心轮带动一杆做定轴转动，杆一端铰支，另一端与偏心轮始终接触，已知偏心轮的角速度，求杆的速度、加速度。
4.平面刚体运动。
具体情形不好意思，忘记了。
用的是基点法，各位只要熟练掌握这部分内容，相信不难解出，像速度投影定理、瞬心法是要掌握的。
PS：以上4题是基础题，共85分。
5.动力学综合。
题目设置的情形为一根绳一端固定于天花板，另一端与杆的一端相连。
初始绳水平，杆足够长而与地面接触。
当绳运动到铅垂时，求杆与地面接触端的速度及地对杆的约束力。
动能定理求速度，动量矩定理求约束力。
6.达朗贝尔原理。
具体的情形不好表述，总之，用了动静法就不能再用动力学的知识解。
7.虚位移定理。
先列虚功方程。
求位移关系时可用坐标变分法和虚速度法。
虚速度法方便些，如此转换为点的合成运动问题。
放心，此题一般不难。
Conclusion：本次试题难在动力学综合，这当然是仁者见仁的看法。
希望各位有志考理论力学的同学，认真复习，理出本课程的主线来，如此即便面对各种考题也能游刃有余。
