南京航空航天大学内部理论力学习题集
- 格式:pdf
- 大小:3.98 MB
- 文档页数:95

第一章 弹性力学基础1-1 上端悬挂、下端自由的等厚度薄板,其厚度为1,容重为ρ。
试求在自重作用下的位移分量表达式。
解:如图1-1建立坐标系.利用x σ沿y 方向均匀分布及x 方向的力平衡条件0=∑x 可得,⎪⎩⎪⎨⎧==-= x l xyy x 00)(τσρσ 又因为1()()x y u u l x x E Eρσσ∂=-=-∂ )()(1x l Eu u E y vx y --=-=∂∂ρσσ 积分得)()21(12y f x lx u +-=Eρ)()(2x f y x l uv +--=Eρ又由对称性 0)(020=⇒==x f v y 由 2110()2xy u v f y uy y x Eτρ∂∂=+=⇒=-∂∂ 综上所述有2221)21(uy Ex lx u ρρ--=Ey x l uv )(--=Eρ1-2 写出图1-2所示平面问题的应力边界条件。
解:上表面为力边界,100=,=,=,m l q lxl X --=Y 。
代入x xy xy y l m Xl m Yσττσ⎧+=⎪⎨+=⎪⎩ 中得到上表面的边界条件为00=--=xy y x q lxl τσσ;=;下表面为自由边,边界条件为000==xy y x τσσ;=;侧面为位移边界。
1-3 矩形板厚为1。
试用应力函数22A xy ϕ=求解。
(并画出面力分布图)解:应力函数22A xy ϕ=满足应力函数表示的变形协调方程,可以作为解。
在无体力的情况下,矩形板的应力为22x Ax yϕσ∂==∂220y x ϕσ∂==∂2xy Ay x yϕτ∂=-=-∂∂根据应力边界条件公式x xy xy y l m X l m Yσττσ+=+=各边的应力边界为a d 边: 0,1l m == 20A X A y h Y ⎧=-=-⎪⎨⎪=⎩ c b 边: 0,1l m ==- 20A X A y hY ⎧==-⎪⎨⎪=⎩a b 边: 1,0l m =-= 0X Y A y⎧=⎪⎨=⎪⎩c d 边: 1,0l m == X A x A lY A y⎧==⎪⎨=-⎪⎩根据以上各边的应力边界条件,可画出矩形板的面力分布图如图1-3a 。

南京航空航天⼤学考研理论⼒学习题册12⼀、概念题1.在⼀组平⾏轴中,刚体对质⼼轴的转动惯量()。
①最⼤②最⼩2.图⽰A、O、C三轴皆垂直于矩形板的板⾯。
已知⾮均质矩形板的质量为m,对A轴的转动惯量为J,点O为板的形⼼,点C 为板的质⼼。
若长度AO = a,CO = e,AC = l,则板对形⼼轴O的转动惯量为()。
①J-ma2②J+ma2③J-m(l2-e2)④J-m(l2+e2)3.图⽰均质圆环形盘的质量为m,内、外直径分别为d和D。
则此盘对垂直于盘⾯的中⼼轴O的转动惯量为()。
①md2/8②mD2/8③m(D2-d2)/8④m(D2+d2)/84.细绳跨过滑轮(不计滑轮和绳的重量),如图所⽰,⼀端系⼀砝码,⼀猴沿绳的别⼀端从静⽌开始以等速v向上爬,猴和砝码等重。
则砝码的速度()。
①⼤⼩等于v,⽅向向下②⼤⼩等于v,⽅向向上③⼤⼩不等于v④砝码不动5.均质杆AB,质量为m,两端⽤张紧的绳⼦系住,绕轴O转动,如图所⽰。
则杆AB对O轴的动量矩为()。
① 5/6ml2ω② 13/12 ml2ω③ 4/3 ml2ω④1/12ml2ω6.均质圆环绕z轴转动,在环中的A点处放⼀⼩球,如图所⽰。
在微扰动下,⼩球离开A点运动。
不计摩擦,则此系统运动过程中()。
①ω不变,系统对z轴动量矩守恒②ω改变,系统对z轴动量矩守恒③ω不变,系统对z轴动量矩不守恒④ω改变,系统对z轴动量矩不守恒7.如图所⽰,⼀半径为R,质量为m的圆轮,在下列两种情况下沿平⾯作纯滚动:(1)轮上作⽤⼀顺时针的⼒偶矩为M的⼒偶;(2)轮⼼作⽤⼀⼤⼩等于M/R的⽔平向右的⼒F。
若不计滚动摩擦,则两种情况下()。
①轮⼼加速度相等,滑动摩擦⼒⼤⼩相等②轮⼼加速度不相等,滑动摩擦⼒⼤⼩相等③轮⼼加速度相等,滑动摩擦⼒⼤⼩不相等④轮⼼加速度不相等,滑动摩擦⼒⼤⼩不相等8.⼀均质杆OA与均质圆盘在圆盘中⼼A处铰接,在图⽰位置时,OA杆绕固定轴O转动的⾓速度为ω,圆盘相对于杆OA的⾓速度也为ω。

第十四章达朗贝尔原理1.平移刚体上的惯性力系向任意点简化,所得主矢相同,R Q =-m a C 。
设质心为C ,点O 到质心的矢径为r C ,则惯性力系向O 点简化的主矩为( )。
① MQO =0② MQO =J O α③ MQO =J C α④ MQO =r C ×R Q正确答案:④2.定轴转动刚体,其转轴垂直于质量对称平面,且不通过质心C ,当角速度ω=0,角加速度α≠0时,其惯性力系的合力大小为R Q =ma C ,合力作用线的方位是( )。
(设转轴中心O 与质心C 的连线为OC ;J C 、J O 分别为刚体对质心及转轴中心的转动惯量)。
① 合力作用线通过转轴轴心,且垂直于OC② 合力作用线通过质心,且垂直于OC③ 合力作用线至轴心的垂直距离为h =J O α / ma C④ 合力作用线至轴心的垂直距离为h =OC +J C α / ma C正确答案:③、④3.刚体作定轴转动时,附加动反力等于零的充分必要条件是( )。
① 转轴是惯性主轴② 质心位于转轴上③ 转轴与质量对称面垂直④ 转轴是中心惯性主轴正确答案:④4.如图所示,质量为m 的质点A ,相对于半径为r 的圆环作匀速圆周运动,速度为u ;圆环绕O 轴转动,在图示瞬时角速度为ω,角加速度为α。
则图示瞬时,质点A 的惯性力为( )。
① )22(ωαu r m F gx +=)/2(22r u r m F gy +=ω② )22(ωαu r m F gx +−=)/2(22r u r m F gy +−=ω③ αmr F gx 2−=)22/(22ωωr u r u m F gy +−=④ 0=gx Fr mu F gy /2−=正确答案:③5.如图所示,半径为r ,质量为m 的均质圆盘与质量也为m 、长为l 的均质杆焊在一起,并绕O轴转动。
在图示瞬时,角速度为ω,角加速度为α 。
则惯性力系向O 点简化结果为( )。
① 2/)23(αm r l F g τ+=2/)23(2ωm r l F gn +=6/)1298(22αm lr r l M gO ++=② 2/)(αm r l F g τ+=2/)(2ωm r l F gn +=6/)1298(22αm lr r l M gO ++=③ 2/)23(αm r l F g τ+=2/)23(2ωm r l F gn +=2/)23(2αm r l M gO +=④ 2/)23(αm r l F g τ+=2/)23(2ωm r l F gn +=4/])(4[22αm r l l M gO ++=正确答案:①6.长度为r 的杆OA 与质量为m 、长度为2r 的均质杆AB 在A 端垂直固接,可绕轴O 转动。



6-1 题6-1图所示平面桁架,各杆Ef 相同,求在载荷P 作用下桁架各杆的内力。
解:(1)解除约束:系统静不定度为K=1,故解除1-2杆的约束, 代之以约束力X 1,如图6-1a 所示。
(2)内力分析:求<<P>>状态下的内力N p 、 单位状态<<1>> 下的内力N 1,内力分别如图6-1b,6-1c 所示。
(3)求典型方程中的影响系数δ11和载荷系数△1PEfdEf l N i i )223(2111+===∑ δ EfPdEf l N N i i P P 2111-===∆∑(4)求解多余约束力X 1:由典型方程01111=∆+P X δ解得:PP d EfEf Pd X P 172.0)223()223(22/1111≈-=+=∆-=δ(5)用叠加原理11X N N N P +=求出各杆的内力PN N P N N P N N P N )12(;)222(;)22(;)223(45342414251312-==-==-==-=6-2 题6-2图所示平面桁架,杆长AD=DC=BC=1m,AC 杆和BD 杆的截面积A AC =A BD =200mm 2,A AD =A DC =A BC =150mm 2, 各杆材料均相同,E =200KN/mm 2,当C 点受垂直载荷P =100KN 作用时,求该结构各杆的内力。
解:(1)解除约束:系统静不定度为K=1,故解除CD 杆的约束, 代之以约束力X 1,如图6-2a 所示。
(2)内力分析:求<<P>>状态下的内力N p 、 单位状态<<1>>下的内力N 1,内力分别如图6-2b,6-2c 所示。
(3)求典型方程中的影响系数δ11和载荷系数△1P1150.0803342111≈+===∑ i i Ef l N δ4316.048093411-≈-===∆∑P Ef l N N i i P P (4)求解多余约束力X 1:由典型方程01111=∆+P X δ解得:755.3663437233480480934/1111≈--=+⨯--=∆-=P P X P δ(5)用叠加原理求出各杆的内力: 11X N N N P +=KN N C B 480.88=-KN N D B 252.3-=-748.46=-C A NKN N D A 877.1=-KN N D C 755.3=-如图6-2d 所示。
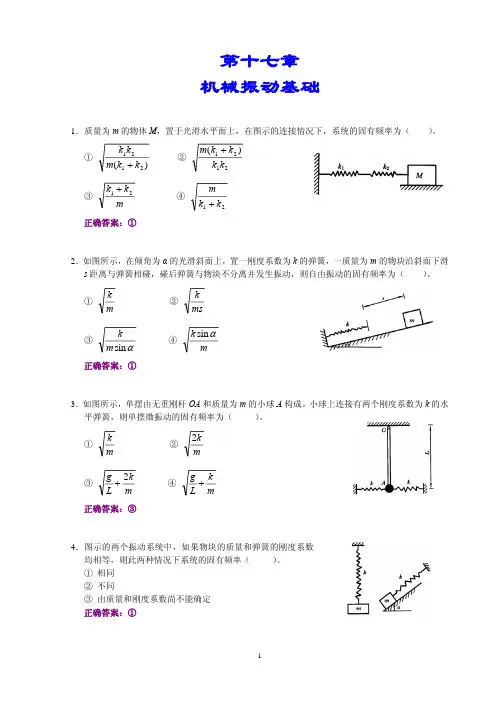
第十七章机械振动基础1.质量为m 的物体M ,置于光滑水平面上,在图示的连接情况下,系统的固有频率为( )。
① )(2121k k m k k + ② 2121)(k k k k m + ③m k k 21+ ④ 21k k m + 正确答案:①2.如图所示,在倾角为α的光滑斜面上,置一刚度系数为k 的弹簧,一质量为m 的物块沿斜面下滑s 距离与弹簧相碰,碰后弹簧与物块不分离并发生振动,则自由振动的固有频率为( )。
① mk ② ms k ③αsin m k ④ m k αsin 正确答案:①3.如图所示,单摆由无重刚杆OA 和质量为m 的小球A 构成。
小球上连接有两个刚度系数为k 的水平弹簧,则单摆微振动的固有频率为( )。
① mk ② m k 2 ③m k L g 2+ ④ m k L g + 正确答案:③4.图示的两个振动系统中,如果物块的质量和弹簧的刚度系数均相等,则此两种情况下系统的固有频率( )。
① 相同② 不同③ 由质量和刚度系数尚不能确定正确答案:①5.图示质量弹簧系统,已知物块的质量为m ,弹簧的刚度系数为k ,静伸长为δs ,原长是l 0 。
若以弹簧未伸长的下端点为坐标原点O ,则物块的运动微分方程为( )。
① 0=+x mk x ② 0)(=−+s x mk x δ ③ g x mk x s =−+)(δ ④ 0)(=++s x mk x δ 正确答案:②6.在图示中,当把弹簧原长的中点O 固定后,系统的固有频率与原来固有频率的比值为( )。
① 21 ② 2③ 2④ 4正确答案:③7.图示弹簧秤,秤盘重未知,当盘上放一重P 的物体时,测得振动周期为T 1;换一重Q 的物体时,其振动周期为T 2,则弹簧的刚度系数应为k =( )。
正确答案:)()(421222T T g P Q −−π8.图示为四根弹簧连接而成的振动装置,弹簧的刚度系数分别为k 1和k 2。
假设质量为m 的物块A 沿倾角为α的斜面作平动,则该振动装置的固有频率ω =( )。
a
A
y
D
q
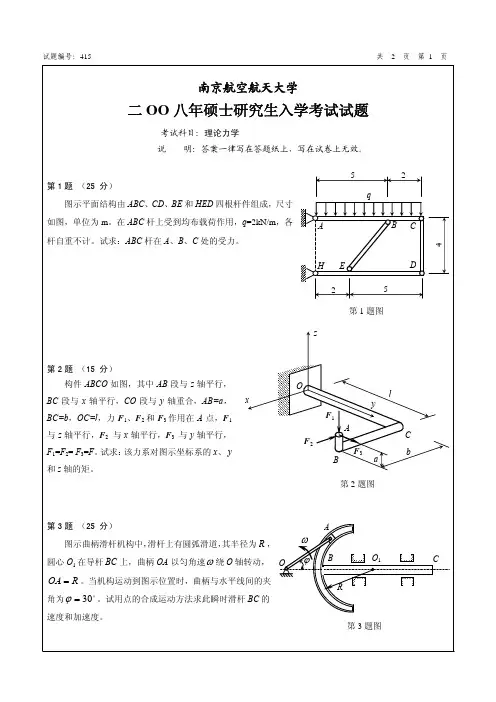
南京航空航天大学
2012年硕士研究生入学考试初试试题( A 卷)
科目代码: 815 科目名称: 理论力学 满分: 150 分
注意:①认真阅读答题纸上的注意事项;②所有答案必须写在答题纸上,写在本试题纸或草稿纸上均无效;③本试题纸须随答题纸一起装入试题袋中交回!
815 理论力学第 1 页共 2 页
815 理论力学第 2 页共 2 页
南京航空航天大学
2013年硕士研究生入学考试初试试题( A 卷)
科目代码: 815 科目名称: 理论力学 满分: 150 分
注意:①认真阅读答题纸上的注意事项;②所有答案必须写在答题纸上,写在本试题纸或草稿纸上均无效;③本试题纸须随答题纸一起装入试题袋中交回!
科目代码:815 科目名称:理论力学第 1 页共 2 页
科目代码:815 科目名称:理论力学第 2 页共 2 页。

大学物理习题集下册物理教学部2007年09月目录部分物理常量┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄练习一压强公式温度┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄练习二理想气体的内能分布律自由程┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄练习三状态方程热力学第一定律┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄练习四等值过程绝热过程┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄练习五循环过程热力学第二定律┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄练习六谐振动┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄练习七谐振动能量谐振动合成┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄练习八波动方程┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄练习九波的能量波的干涉┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄练习十驻波┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄练习十一光的相干性双缝干涉光程┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄练习十二薄膜干涉劈尖┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄练习十三牛顿环迈克耳逊干涉仪光的衍射┄┄┄┄┄┄┄┄┄┄┄┄┄练习十四单缝┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄练习十五光栅衍射┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄练习十六光的偏振┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄练习十七光电效应德布罗意波不确定关系┄┄┄┄┄┄┄┄┄┄┄┄┄┄部分物理常量万有引力常量 G=6.67×10-11N·m2·kg-2重力加速度 g=9.8m/s2=6.02×1023mol-1阿伏伽德罗常量 NA摩尔气体常量 R=8.31J·mol-1·K-1玻耳兹曼常量 k=1.38×10-23J·K-1标准大气压 1atm=1.013×105Pa真空中光速 c=3.00×108m/s部分数学常量 1n2=0.693 1n3=1.099基本电荷 e=1.60×10-19C=9.11×10-31kg电子静质量 me=1.67×10-27kg质子静质量 mn=1.67×10-27kg中子静质量 mp= 8.85×10-12 F/m真空介电常量ε真空磁导率μ=4π×10-7H/m=1.26×10-6H/m普朗克常量 h = 6.63×10-34 J·s维恩常量 b=2.897×10-3m·K2练习一 压强公式 温度一.选择题1. 一个容器内贮有1摩尔氢气和1摩尔氦气,若两种气体各自对器壁产生的压强分别为p 1和p 2,则两者的大小关系是:(A) p 1>p 2 . (B) p 1<p 2 . (C) p 1= p 2 . (D) 不确定的.2. 一定量的理想气体贮于某一容器中,温度为T ,气体分子的质量为m . 根据理想气体的分子模型和统计假设,分子速度在x 方向的分量平方的平均值为:(A) 2x v =m kT 3. (B) 2x v = (1/3)m kT 3. (C) 2x v = 3kT /m . (D) 2x v = kT/m .3. 下列各式中哪一式表示气体分子的平均平动动能?(式中M 为气体的质量,m 为气体分子质量,N 为气体分子总数目,n 为气体分子数密度,N 0为阿伏伽德罗常数)(A) [3m/(2M )] pV . (B) [3M/(2M mol )] pV . (C) (3/2)npV .(D) [3M mol /(2M )] N 0pV .4. 关于温度的意义,有下列几种说法: (1) 气体的温度是分子平动动能的量度.(2) 气体的温度是大量气体分子热运动的集体表现,具有统计意义. (3) 温度的高低反映物质内部分子运动剧烈程度的不同. (4) 从微观上看,气体的温度表示每个气体分子的冷热程度. 上述说法中正确的是(A) (1)、(2)、(4) . (B) (1)、(2)、(3) . (C) (2)、(3)、(4) . (D) (1)、(3)、(4) .3二.填空题1. 在容积为10 2m 3的容器中,装有质量100g 的气体,若气体分子的方均根速率为200m/s ,则气体的压强为 .2. 如图13.1所示,两个容器容积相等,分别储有相同质量的N 2和O 2气体,它们用光滑细管相连通,管子中置一小滴水银,两边的温度差为30K ,当水银滴在正中不动时,N 2的温度T 1= ,O 2的温度T 2= .( N 2的摩尔质量为28×10-3kg/mol,O 2的摩尔质量为32×10-3kg/mol.)3. 理想气体的分子模型是(1)分子可以看作 ; (2)除碰撞时外,分子之间的力可以 ; (3)分子与分子的碰撞是 碰撞.三.证明题1. 试从温度公式(即分子热运动平均平动动能和温度的关系式)和压强公式推导出理想气体的状态方程.图13.14练习二 理想气体的内能 分布律 自由程一.选择题1. 理想气体的内能是状态的单值函数,下面对理想气体内能的理解错误的是 (A) 气体处于一定状态,就具有一定的内能; (B) 对应于某一状态的内能是可以直接测量的;(C) 当理想气体的状态发生变化时,内能不一定随之变化; (D) 只有当伴随着温度变化的状态变化时,内能才发生变化;2. 两瓶质量密度ρ相等的氮气和氧气,若它们的方均根速率也相等,则 (A) 它们的压强p 和温度T 都相等. (B) 它们的压强p 和温度T 都都不等. (C) 压强p 相等,氧气的温度比氮气的高. (D) 温度T 相等, 氧气的压强比氮气的高.3. 密闭容器内贮有1mol 氦气(视为理想气体),其温度为T ,若容器以速度v 作匀速直线运动,则该气体的能量为(A) 3kT .(B) 3kT /2 +M mol v 2 /2. (C) 3RT /2.(D) 3RT /2+M mol v 2 /2. (E) 5RT /2. 4. 如图14.1所示为某种气体的速率分布曲线,则()⎰21d v v v v f 表示速率介于v 1到 v 2之间的(A) 分子数.(B) 分子的平均速率.(C) 分子数占总分子数的百分比. (D) 分子的方均根速率.5. 一容器中存有一定量的理想气体,设分子的平均碰撞频率为z ,平均自由程为λ,则当温度T 升高时(A) z 增大,λ减小. (B) z 、λ都不变. (C) z 增大,λ不变. (D) z 、λ都增大.二.填空题图14.151. 如图14.2所示两条曲线(1)和(2),分别定性的表示一定量的某种理想气体不同温度下的速率分布曲线,对应温度高的曲线是 .若图中两条曲线定性的表示相同温度下的氢气和氧气的速率分布曲线,则表示氧气速率分布曲线的是 .2. A 、B 、C 三个容器中装有同一种理想气体,其分子数密度之比为n A :n B :n C = 4:2:1,而分子的方均根速率之比为2A v :2B v :2C v =1:2:4。

南京航空航天大学往年真题及答案541
南京航空航天大学往年真题及答案:
一、流体力学真题及答案
1、压强对流体速度的影响?
答:随着压强的增加,流体的速度也会增加。
当流体的压强升高时,流体的速度也会相应增加,因此,压强对流体速度有一定的影响。
2、不可压缩性流体容积变化的影响?
答:不可压缩性流体容积变化影响流体运动。
由于不可压缩性流体的容积变化较大,所以它对流体的运动有明显的影响,一般不可压缩性流体的压力流量关系月亮比可压缩性流体的要灵活。
3、流体可延展性的特点?
答:流体可延展性是指流体受到外力作用时,受力面上的位移量(或者旋转量)要大于介质的某一原始位移量(或者旋转量)。
例如,流体受到激励时可以由其原有的形状发生变形,并在受力时产生压缩或膨胀。
二、雷达原理真题及答案
1、雷达波的发射原理?
答:雷达波的发射原理是,首先将施加在发射天线端的一个很大的高频电压通过加网(主频网)中的一个变压器击穿空气的绝缘介质,从而产生高能量电磁波,然后经过发射天线发射出去。
2、接收雷达波的原理?
答:接收雷达波的原理是通过接收天线把接收到的微弱电磁波能量聚集起来,并将其加以增强后,使其能够通过加网(主频网)中的一个变压器击穿空气绝缘介质,从而产生低频信号,由此来接收雷达波信号。
3、航法定位所用的雷达原理?
答:航法定位使用的雷达原理是通过测量特定频率的雷达信号的电磁波的脉冲宽度、瞬变率和相位等参数,以确定雷达波发射方向和物体距发射方向的距离和位置,从而实现航法定位。
第十三章动 能 定 理1.如图所示,半径为R ,质量为m 1的均质滑轮上,作用一常力矩M ,吊升一质量为m 2的重物。
当重物上升高度h 时,力矩M 所作的功为( )。
① Mh /R② m 2gh③ Mh/R -m 2gh④ 0正确答案:①2.三棱柱B 沿三棱柱A 的斜面运动,三棱柱A 沿光滑水平面向左运动。
已知A 的质量为m 1,B 的质量为m 2;某瞬时A 的速度为v 1,B 沿斜面的速度为v 2。
则此时三棱柱B 的动能为 ( )。
① 22221v m ② 2212)(21v v m − ③ )(2122212v v m − ④ ]sin )cos [(212222212θθv v v m +− 正确答案:④3.一质量为m ,半径为r 的均质圆轮以匀角速度ω沿水平面作纯滚动,均质杆OA 与圆轮在轮心O 处铰接,如图所示。
设OA 杆长l = 4r ,质量M = m /4。
在图示杆与铅垂线的夹角φ = 60°时,其角速度ωOA = ω/2,则此时该系统的动能为( )。
① 222425ωmr T =② 221211ωmr T = ③ 2267ωmr T = ④ 2232ωmr T = 正确答案:③4.均质圆盘A ,半径为r ,质量为m ,在半径为R 的固定圆柱面内作纯滚动,如图所示。
则圆盘的动能为( )。
① 2243ϕ mr T = ② 2243ϕ mR T = ③ 22)(21ϕ r R m T −= ④ 22)(43ϕ r R m T −= 正确答案:④5.图示均质圆盘沿水平直线轨道作纯滚动,在盘心移动了距离s 的过程中,水平常力F T 的功A T =( );轨道给圆轮的摩擦力F f 的功A f =( )。
① F T s② 2F T s③ 0④ -F f s正确答案:② ③6.图示二均质圆盘A 和B ,它们的质量相等,半径相同,各置于光滑水平面上,分别受到F 和F ′的作用,由静止开始运动。
大学物理(力学相对论热学电磁学)_南京航空航天大学中国大学mooc课后章节答案期末考试题库2023年1.关于力距有以下几种说法:(1)内力矩不会改变刚体对某个定轴的角动量;(2)作用力和反作用力对同一轴的力矩之和必为零;(3)质量相等形状和大小不同的两个刚体,在相同力矩作用下,它们的角加速度一定相等。
在上述说法中:答案:(1)、(2)是正确的2.一容器装着一定量的某种气体,下述几种说法哪一种对?答案:容器内各部分压强相等,且各部分密度也相同,这状态一定是平衡态3.一块铜板垂直于磁场方向放在磁感强度正在增大的磁场中时,铜板中出现的涡流(感应电流)将答案:减缓铜板中磁场的增加4.一水平圆盘可绕通过其中心的固定竖直轴转动,盘上站着一个人.把人和圆盘取作系统,当此人在盘上随意走动时,若忽略轴的摩擦,此系统答案:对转轴的角动量守恒5.假设卫星环绕地球中心作圆周运动,则在运动过程中,卫星对地球中心的答案:角动量守恒,动能守恒,动量不守恒6.一人站在转台中心,设转轴光滑,人的两手各握一重物并伸直,如图3-6所示。
以人、转台和重物为系统,在人向自身胸部收回双手的过程中,有以下4种说法: (1) 系统的转动惯量减小; (2) 系统转动的角速度增大; (3) 系统的角动量保持不变; (4) 系统的转动动能保持不变。
以上说法中正确的是【图片】答案:(1)(2)(3)7.一匀质细杆可绕通过上端与杆垂直的水平光滑固定轴O旋转,初始时静止。
现有一个小球自左方垂直打击细杆,如图3-7所示。
设小球与细杆的碰撞为非弹性碰撞。
以杆和球为系统,在碰撞过程中系统的【图片】答案:对转轴O的角动量守恒8.关于力矩有以下几种说法: (1)对某个定轴而言,内力矩不会改变刚体的角动量; (2)作用力和反作用力对同一轴的力矩之和必为零; (3)质量相等,形状和大小不同的两个刚体,在相同力矩的作用下,它们的角加速度一定相等。
上述说法中正确的是答案:(1)(2)9.均匀细杆OM能绕O轴在竖直平面内自由转动,如图3-12所示。
第八章点的合成运动1.动点的牵连速度是指该瞬时牵连点的速度,它所相对的坐标系是()。
①动坐标系②不必确定的③定坐标系④都可以正确答案:③2.点的速度合成定理v a = v e + v r 的适用条件是()。
①牵连运动只能是平动②各种牵连运动都适合③牵连运动只能是转动④牵连运动为零正确答案:②3.两曲柄摇杆机构分别如图(a)、(b)所示。
取套筒A为动点,则动点A的速度平行四边形()。
①图(a)、(b)所示的都正确②图(a)所示的正确.,图(b)所示的不正确③图(a)所示的不正确.,图(b)所示的正确④图(a)、(b)所示的都不正确正确答案:②4.图示偏心凸轮如以匀角速度ω绕水平轴O逆时针转动,从而推动顶杆AB沿铅直槽上下移动,AB杆的延长线通过O点。
若取凸轮中心C为动点,动系与顶杆AB固连,则动点C的相对运动轨迹为( )。
①铅直直线②以O点为圆心的圆周③以A点为圆心的圆周④无法直接确定正确答案:③5.在图示机构中,已知s = a + b sinωt,且φ= ωt(其中a、b、ω均为常数),杆长为L,若取小球A为动点,动系固连于物块B,定系固连于地面,则小球A的牵连速度v e的大小为( );相对速度v r的大小为( )。
①Lω② bωcosωt③bωcosωt + Lωcosωt④bωcosωt + Lω正确答案:②①6.图示偏心轮摇杆机构中,ω、α为已知,要求摇杆的角加速度α1,应取( )。
① 杆上的M 为动点,轮为动系② 轮上的M 为动点,杆为动系③ 轮心C 为动点,杆为动系④ 轮心C 为动点,轮为动系正确答案:③7.如图所示,直角曲杆以匀角速度ω绕O 轴转动,套在其上的小环M 沿固定直杆滑动。
取M 为动点,直角曲杆为动系,则M 的( )。
① v e ⊥CD ,a C ⊥CD② v e ⊥OM ,a C ⊥CD③ v e ⊥OM ,a C ⊥OM④ v e ⊥CD ,a C ⊥OM正确答案:②8.平行四边形机构如图。