极坐标下的质点运动

质点在极坐标系中的运动分析在物理学中，质点在极坐标系中的运动是一种常见的运动形式。

极坐标系是一种由径向和角度两个坐标轴组成的坐标系，对于描述圆形或者旋转运动的物体非常有用。

在本文中，我们将探讨质点在极坐标系中的运动特点以及相关的物理概念。

首先，我们来介绍一下极坐标系的基本概念。

在极坐标系中，一个质点的位置可以由径向距离和角度来确定。

径向距离表示质点与原点之间的距离，而角度则表示质点所在位置相对于参考方向的角度。

这种坐标系的特点是能够直观地描述物体的旋转和径向运动。

接下来，我们将讨论质点在极坐标系中的运动方程。

对于质点在极坐标系中的运动，我们可以通过径向速度和角速度来描述。

径向速度表示质点沿着径向的运动速度，而角速度则表示质点绕原点旋转的速度。

根据牛顿第二定律，我们可以得到质点在极坐标系中的运动方程：质点的径向加速度等于质点的径向力除以质量，即：a_r = F_r / m质点的角加速度等于质点的角力矩除以质量，即：α = τ / I其中，F_r表示径向力，m表示质量，τ表示角力矩，I表示转动惯量。

在质点的运动过程中，我们还需要考虑到质点的角动量和角动量守恒定律。

角动量表示质点绕原点旋转的动量，可以用以下公式表示：L = Iω其中，L表示角动量，I表示转动惯量，ω表示角速度。

根据角动量守恒定律，当质点在极坐标系中的运动过程中没有外力或者外力矩作用时，质点的角动量保持不变。

这意味着质点的转动惯量和角速度的乘积保持不变。

此外，我们还需要了解质点在极坐标系中的运动特点。

质点在极坐标系中的运动可以是径向运动、角度运动，或者同时具有径向和角度运动。

径向运动表示质点沿着径向方向的运动，可以是向内或者向外的运动。

角度运动表示质点绕原点旋转的运动，可以是顺时针或者逆时针的运动。

质点的运动轨迹可以是圆形、椭圆形或者其他形状，取决于质点的运动方程和初始条件。

最后，我们来看一个实例来更好地理解质点在极坐标系中的运动分析。

一、填空题 1、质点运动方程为 r = a t ，θ= bt ，则极坐标下的轨道方程为 ，加速度大小为 。

[θbar =；224t b ab +；221t b a +] 1、质点运动方程为t b y t a x ωωsin ,cos ==（b a ,为常数）其轨道方程为 ，速度大小为 。

[t b t a v by a x ωω22222222cos sin ;1+==+] 2、单位质量的两个质点位于xy 平面上运动，在某时刻其位矢、速度分别为j i v j i v j i r j i r52,,32,32121+=-=+=+= 则此时质心位矢=c r ，质心速度为=c v ，质系动量=p，质系动能T= ，质系对原点的角动量=J。

[)43(21j i r c+=)43(21j i v c +=；j i p43+= ；T=31/2；k J 2=] 3、质量均为1的三个质点组成一质系，若其瞬时速度分别为i v k v j v3,2,2321==-=，则质系的动量为 ，质心速度为 。

[k j i223+- ；k j i3232+-]3、质量均为1的三个质点组成一质系，某时刻它们的位矢分别为,2,,32321k j r j i r k j i r+=+=++=，则质系的质心位矢为 。

[k j i r c322++=] 4、已知质点势能为)(2122y x V +=，则保守力=F 。

[j y i x F --=]5、当质点受有心力作用时，其基本守恒律的数学表达式为 和 。

[h r =θ2；E r V r rm =++)()(2122θ ] 6、一个圆盘半径为r ，质量为m ，沿直线作纯滚动，盘心速度为c v，则圆盘的转动角速度=ω ，圆盘的绝对动能T= 。

[r v c /=ω；2224121ωmr mv T c +=] 7、标出下列两图中作平面运动刚体的转动瞬心的位置：7、标出下列两图中作平面运动刚体的转动瞬心的位置：V AV BV V B VV B V A V BcV AV B VV B c V A V BcV V B c8、作用在刚体上的力可沿力的作用线任意移动而不影响它的作用效果，这叫 ，因此作用在刚体上的力是 矢量。

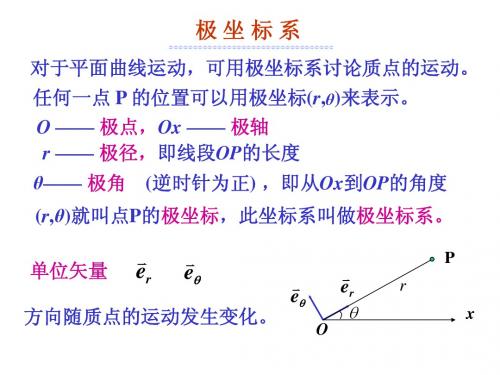
活动坐标系以极坐标系下任意点P(r,θ)为原点，建立一个活动坐标系，该坐标系的两个主方向分别为径向(radial)和横向(transverse)。

径向与OP⃗⃗⃗⃗⃗ 的方向一致。

横向与径向垂直且朝向θ增加的方向。

该坐标系下的任一点或物理量可以通过主方向上的两个单位矢量（基）表示出来。

例如，假设P是一运动质点，则它的速度和加速度可以分解为v P=v r e r+vθeθ,a P=a r e r+aθeθ其中e r是径向单位矢量，eθ是横向单位矢量。

e r的直角坐标表示可以通过对OP⃗⃗⃗⃗⃗ 单位化获得。

e r=OP⃗⃗⃗⃗⃗|OP|=(cosθ,sinθ)而eθ的直角坐标表示可将e r逆时针旋转90°获得。

eθ=(−sinθ,cosθ)可以看出，{e r,eθ,P(r,θ)}刚好也是一个右手系。

并且该活动坐标系是与r的取值无关的（只要r≠0）。

所以当点P径向运动时，活动坐标系不发生改变；只有当点P有横向运动分量时活动坐标系才会发生改变。

e r,eθ关于θ的导数ddθe r=(−sinθ,cosθ)=eθddθeθ=−(cosθ,sinθ)=−e r极坐标系下的速度方法一设质点P(r,θ)的运动方程为{r=r(t)θ=θ(t)。

以时刻t为起点，建立活动坐标系{e r,eθ,P(r(t),θ(t))}，则经过∆t时刻质点运动到P′=[r(t+∆t)−r(t)]e r+[θ(t+∆t)−θ(t)]r(t)eθ因此，在时刻t，质点速度在坐标系{e r,eθ,P(r(t),θ(t))}下可以表示为v P=lim∆t→0PP′∆t=ṙe r+rθeθ其中，径向速度为ṙ，横向速度为rθ。

方法二以r P代表质点P的坐标。

r P(t)就代表了质点P的运动方程。

由于r P(t)=(r(t)cosθ(t),r(t)sinθ(t))=r(t)e r(t)所以d dt r P(t)=ddt(r(t)e r(t))=(ddtr(t))e r(t)+r(t)(ddte r(t))其中d dte r=de rdθ·dθdt=θeθ这一项可以理解为由质点位置矢量的方向(e r)改变所引起的。

第一章 质点运动学§1-1 质点运动的矢量描述与直角坐标描述一、参考系和坐标系有一定大小且不变形的物体, 或几个相对位置保持不变的物体, 都可以作为参考系. 一个点不能作参考系！坐标系可以看成是由坐标曲线组成的带有标度的空间网格.各种坐标系的坐标曲线都在它们的交点处互相正交, 都属于正交曲线坐标系.沿质点所在位置的坐标曲线切线方向建立的一组单位矢量称为坐标系的基矢. 直角坐标系Oxyz (坐标曲线321,,c z c y c x ===),基矢为单位矢量k j i ,,, 按惯例我们使用的坐标系 全是右手正交系, 其基矢满足如下关系: k j i =× 0=⋅=⋅=⋅i k k j j i 若坐标系的空间网格相对参考系固定不动, 则该坐标系相对参考系固定不动, 这时我们称该 坐标系与参考系固连.二、自由度我们称确定力学系统位置所需要的独立坐标 数为系统的自由度, 自由度记为s .三、运动学方程和轨道图中我们用直角坐标系Oxyz 代表参考系, 位置矢量(简称位矢)r e r r = )(t r r =称为质点的运动学方程, 它包括了质点运动的全 部信息. 质点运动的轨道即为位置矢量r 的矢端曲线.在直角坐标系Oxyz 中 k z j y i x r ++=运动学方程的分量形式为)(),(),(t z z t y y t x x ===由式中消去时间t , 则得到轨道方程.四、位移和路程位移是质点位置矢量的增量, )()Δ(Δt r t t r r −+=路程是质点沿轨道走过的长度, 为一恒正标 量, 记为s ∆,AB s =∆弧长.注意s r ΔΔ≠s r ΔΔ≠r r ΔΔ≠但当0Δ→t 时,B A ,间弦长与弧长相等, s r ∆→∆ , 或记为s r d d =五、速度瞬时速度矢量简称为速度, 被定义为位置矢量对时间的导数,r t r t r v t ==∆∆=→∆d d lim 0 速度的方向沿轨道 (即r 的矢端曲线) 的切线指向运动的前方, 它的大小为速率v ,s ts t rt r v v t ===∆∆==→∆d d d d lim0 在直角坐标系Oxyz 中, k z j y i x v ++=.六、加速度瞬时加速度矢量简称加速度, 定义为速度对时间的导数,r t r v t v t v a t ====∆∆=→∆220d d d d lim 加速度a 一定指向轨道的凹侧. 若将不同时刻的速度矢量的矢尾集中于一点, 则可得出速度矢量v 的矢端曲线即速端曲线. 加速度a 沿速端曲线切线方向并指向v 的矢端沿速端曲线运动的前方, 加速度的大小a 等于v 的矢端沿速端曲线运动的速率.任意矢量A 对时间的导数A 的方向沿A 的矢端曲线的切线, 其指向与A 的矢端沿矢端曲线的运动方向一致; A 的大小即A 的矢端沿矢端曲线运动的速率.在直角坐标系Oxyz 中, k zj y i x k v j v i v a z y x ++=++=§1-2 质点运动的平面极坐标描述当质点被限制在一个平面上运动时, 其自由度2=s , 我们建立与参考系固连的极坐标系. 质点P 的位置由坐标量r 和θ确定, 要明确极角θ的正方向 (即θ的增加方向)!平面极坐标系是正交曲线坐标系, 其平面坐标网格由一组同心圆(1c r =)及一组放射状半直线(2c =θ)组成.平面极坐标系的基矢为r e 和θe .0=⋅θe e r .r e 的方向为径向, θe 的方向为横向.)(θr r e e = ,)(θθθe e =. 我们把矢量沿质点所在位置的基矢 “就地” 进行正交分解.在极坐标系中, 质点的运动学方程为[])()(t e t r r r θ =标量形式)(),(t t r r θθ==消去时间t , 则得到轨道方程0),(=θr f .根据速度的定义, 把[])()(t e t r r r θ = 对时间求导数, 得到 t e r e t r t r v r r d d d d d d +==下面求单位矢量r e 的时间 导数t e r d d ,t e t t e t t e t e r t r r t r ∆∆=∆−∆+=→∆→∆ 00lim )()(lim d d 当0→∆t 时,0→∆θ. 注意到由r e 及r e ∆组成的矢量三角形为腰长为1的等腰三角形, 所以当0→∆t 时r e ∆与r e 垂直, 且θ∆⋅=∆1r e . 由于0→∆θ且0Δ>θ时r e ∆与θe 方向相同, 所以0→∆t 时θθe e r ⋅∆=∆, 故 θθθθe e tt e t r ⋅=∆∆=→∆0lim d d于是得到极坐标系中的速度表达式,θθe r e rv r += rv r =称为径向速度, θθ r v =称为横向速度. 根据加速度的定义,得)(d d d d θθe r e r tt v a r +==t e r e r e r e r e r r d d θθθθθθθθ ++++=下面改换一个方法求t e d d θ . 由于θe 为单位矢量, 故θe 的矢端曲线为半径为1的单位圆. 0Δ>θ 时, θe 的矢端沿其矢端曲线运动的速率为θ ⋅1, t e d d θ 的方向沿矢端曲线切线, 其指向如图所示,故可知 r e te θθ−=d d 同样,θθe t e r =d d于是得到极坐标系中加速度的表达式θθθθe r r e r r a r )2()(2++−=2θ r r a r −=和θθθ r r a 2+=分别称为径向加速度和横向加速度.矢量的变化为矢量大小的变化及矢量方向的变化二者产生效果的叠加, 请读者试用这种观点分析式中各项是如何产生的. 还可用运动分解和合成的观点理解式中各项的意义.例题1半径为R 的铁圈上套一小环P , 直杆OA 穿过小环P 并绕铁圈上O 点以匀角速度ω转动. 求小环P 的运动方程、 轨道方程、 速度和加速度.解 如图所示建立极坐标系，设0=t 时0θθ=， 则运动学方程为+=+=00)cos(2θωθθωt t R r 轨道方程为θcos 2R r =速度和加速度为 θθe r e r v r += θθωωθωωe t R e t R r )cos(2)sin(200+++−= θθθθe r r e r r a r )2()(2++−= θθωωθωωe t R e t R r )sin(4)cos(40202+−+−=本例题也可用图中直角坐标系xyz O 2求解, 由读者自行完成. 请读者另行验证:(1) 不同方法中a v ,表达式不同, 但它们对描述P点运动是等价的;(2) 不同方法中a v ,的大小和方向是惟一确定的.例题1是运动学正问题, 即先写出运动学方程,通过求导数运算求出v 和a . 运动学逆问题是已知速度或加速度及初条件求运动学方程, 使用的数学方法是积分或解微分方程, 和正问题比较要复杂一些, 但只要把握解题的方向也是不难解决的.例题2 已知一质点做平面运动， 其速率为常量c ，其位置矢量转动的角速度亦为常量0ω，试求质点的运动学方程及轨道方程. 设0=t 时，0=r , 0=θ.解 由已知条件ωθ= (1) 2222c r r =+θ (2) 把（1）是式化为t d d 0ωθ=，积分并由0=t 时0=θ定积分常数，可得t 0ωθ= (3)把（1）式代入（2）式，分离变量得t r c r d d 2202±=−ω 积分并以0=t 时0=r 定积分常数，得t c r 00sin ωω±= (4) （3）（4）二式即为运动学方程=±=t t c r 000sin ωθωω 消去t 得轨道方程θωsin 0c r ±= 轨道为两个圆，如图所示.柱坐标系可以看成是由Oxy 平面内的极坐标系 (坐标量为ρ和θ) 及z 轴构成的三维空间坐标系. 其空间坐标网格由1c =ρ的圆柱面、 2c =θ的放射状半平面和3c z =的平面3组曲面相交形成的曲线所组成. 质点位置由坐标量z ,,θρ确定. 柱坐标系的基矢为单位矢量θρe e ,和k . 柱坐标系为右手正交系, 其基矢满足如下关系:k e e =×θρ质点的运动学方程为 []k t z t e t t r r )()()()(+==θρρ速度和加速度的表达式为 k z e e v ++=θρθρρk z e e a +++−=θρθρθρθρρ)2()(2 推导请仿照§1-2自己完成.球坐标系如图所示, 质点P 的位置由坐标量ϕθ,,r 确定. 球坐标系的空间坐标网格由1c r =的球面、 2c =θ的圆锥面和3c =ϕ的放射状半平面3组曲面相交形成的曲线所组成.球坐标系的基矢为r e ，θe ，ϕe .r e 沿位矢r 的方向, θe 和ϕe 的指向与θ和ϕ的正方向一致. 球坐标系为右手正交系, 其基矢满足如下关系:ϕθe e e r =×0=⋅=⋅=⋅r r e e e e e e ϕϕθθ球坐标系中的θ亦称为极角、 ϕ称为方位角. 球坐标系中的基矢不是常矢量, 其中r e 为θ和ϕ的函数. 我们把矢量沿质点所处位置的基矢r e ，θe 和ϕe “就地”进行正交分解.质点的运动学方程为 [])(),()()(t t e t r t r r r ϕθ ==下面我们从速度的定义导出球坐标系中的速度表达 式. 将r ∆沿t 时刻质点所在位置的基矢正交分解, 得到ϕθe s e s e s r r 321∆+∆+∆=∆当0→∆t 时, r s ∆→∆1，2s ∆和3s ∆可用坐标曲线上的弧长来表示, 即θ∆→∆r s 2和ϕθ∆⋅→∆sin 3r s 于是可知 t e r e r e r t r t r v r t t ∆∆⋅+∆+∆=∆∆==→∆→∆ϕθϕθθ sin lim lim d d 00 ϕθθϕθe r e r e rr sin ++= 球坐标系中的加速度公式可按矢量导数定义求导得出, 但比较复杂, 我们将在后面用分析力学的方法导出.§1-5 质点运动的自然坐标描述利用质点运动轨道本身的几何特性 (如切线、法线方向等)来描述质点的运动. 这种方法称为自然坐标法.一、弧长方程在轨道上取一点作原点O , 规定沿轨道的某一方向为弧长的正方向, 质点位置可由原点O 到质点间的一段弧长s 来确定, s 称为弧坐标.)(t s s =上式称为弧长方程. 弧长方程和轨道方程一起与质点的运动学方程等价.弧坐标s 为可正可负的标量, 与恒正的路程是不同的.二、相关的微分几何知识轨道上无限接近的两个点所决定的直线称为切线. 定义切向单位矢量t e 沿切线, 其指向与弧长正方向一致. 沿t e 的方向称为切向.轨道上无限接近的3个点确定的平面, 即无限接近的两条切线所确定的平面, 称为密切面.密切面取向的改变反映了曲线的挠曲情况.轨道曲线上无限接近的3个点所决定的圆称为曲率圆, 曲率圆在密切面内. 曲率圆的圆心称为曲率中心, 曲率圆的半径ρ称为曲率半径, 曲率半径的倒数ρκ1=称为曲率.设弧长s P P d =′, 显然s d d 1ϕρκ==, 曲率κ越大则曲线弯曲程度越大. 当轨道为平面曲线)(x y y =时, 可利用数学分析中的公式 []23222)d d (1d d 1x y x y +==ρκ求曲率κ及曲率半径ρ.过轨道上一点, 与切线垂直的线称为法线. 法线有无限多条,它们组成的平面称为法平面.密切面内的法线称为主法线, 定义主法向单位矢量n e 沿主法线指向曲率中心. 沿n e 的方向称主法向, n e 指向轨道凹侧.垂直于密切面的法线称为副法线. 定义副法向单位矢量b e 沿副法线, 指向n t e e ×的方向.n t b e e e ×=沿b e 的方向为副法向.单位矢量b n t ,,e e e 两两互相垂直, 并成右手螺旋关系.三、速度和加速度表达式把质点的速度和加速度沿质点所在处的单位矢量b n t ,,e e e “就地”正交分解, 进而导出质点的速度和加速度表达式.速度沿切线指向运动的前方, 所以0b n ==v v . 考虑到0>s 时v 与t e 同向, 故 t t t e se v v == 速度的大小sv v v ===t . 由加速度的定义 t e s e s e s t t v a d d )(d d d d t t t +===当ϕ的正向与弧长s 正向一致时, ϕρd d =s ,故ρρϕt v s == . 所以 n n n t d d 1d d e s e e t t e ρϕϕ==⋅=因此 n t e s e s a ρ2+=s v a ==t t 称为切向加速度, 是由于速度t t e v v =的大小改变而产生的. ρρ22n s v a ==称为法向加速度, 是由于速度的方向改变而产生的. 由于n a 恒正, 故a 一定指向轨道凹侧, 与§1-1中结论一致. 0b ≡a 说明对任何空间曲线运动,加速度a 必在密切面内, 这是加速度和密切面定义导致的必然结果.注意原点O 的选定和弧长正方向的规定! 在自然坐标描述中, 需要已知质点运动的轨道, 而对轨道的数学描述又需要一个坐标系, 所以必须掌握自然坐标描述中的物理量与其他坐标系中的物理量之间的联系. 建立这个联系的基本依据是: 速度v 和加速度a 在不同的描述方法中有不同的表达形式, 但它们的大小和方向是惟一确定的.例题1半径为R 的铁圈上套一小环P , 直杆OA 穿过小环P 并绕铁圈上O 点以匀角速度ω转动. 求小环P 的运动方程、 轨道方程、 速度和加速度.解 曾用如图所示建立极坐标系求解.此例题也可用自然坐标法求解: 以1O 为原点，规定弧长正方向如图所示.轨道已知，弧长方程为)(20θω+=t R s速度和加速度为 t e R e s v ω2t == n 2n 2t 4)(e R e s e sa ωρ=+= 比其它方法简单!自然坐标描述并不是自然坐标系中的描述.请读者验证: (1) 不同方法中a v ,表达式不同, 但它们对描述P点运动是等价的; (2) 不同方法中a v ,的大小和方向是惟一确定的.例题3 已知质点的运动学方程为t R x ωcos = t R y ωsin = t h z ωπ2= （h R ,,ω为常量）试分析质点的运动，求切向加速度、法向加速度及轨道的曲率半径。

高中物理质点的运动质点运动是物理学中一个重要的概念，指的是忽略物体自身形状和大小，只考虑物体质心的运动。

在高中物理学中，质点运动是一个基础而重要的内容，它包括质点的位置、速度和加速度等方面的研究。

本文将从不同的角度来探讨质点运动的基本原理和相关概念。

一、质点的位置质点的位置是指质点在空间中的坐标，通常用直角坐标系或极坐标系来表示。

在直角坐标系中，我们可以用x、y、z三个分量来描述质点的位置。

如果质点只在一个平面内运动，我们也可以只用x、y两个分量来表示。

质点的位置随时间的变化而变化，可以用位置函数来描述。

对于平直运动的质点，其位置函数可以表示为：x = x0 + vt其中，x是质点的位置，x0是初始位置，v是质点的速度，t是时间。

二、质点的速度质点的速度是指质点在单位时间内的位移量。

速度有大小和方向两个方面。

在直角坐标系中，我们可以用速度矢量v来表示质点的速度，其大小为v = √(v_x² + v_y² + v_z²)，其中v_x、v_y、v_z是质点在x、y、z三个坐标轴上的速度分量。

质点的速度随时间的变化而变化，可以用速度函数来描述。

对于匀加速直线运动的质点，其速度函数可以表示为：v = v0 + at其中，v是质点的速度，v0是初始速度，a是质点的加速度，t是时间。

三、质点的加速度质点的加速度是指质点在单位时间内速度的变化量。

加速度也有大小和方向两个方面。

在直角坐标系中，我们可以用加速度矢量a来表示质点的加速度，其大小为a = √(a_x² + a_y² + a_z²)，其中a_x、a_y、a_z是质点在x、y、z三个坐标轴上的加速度分量。

质点的加速度可以分为两类：匀速直线运动和匀加速直线运动。

在匀速直线运动中，质点的速度保持不变，加速度为零；而在匀加速直线运动中，质点的加速度保持不变，速度随时间线性增加或减小。

四、质点运动的类型根据质点在空间中运动轨迹的不同，质点的运动可以分为直线运动和曲线运动两种类型。