惯性系下质点运动学

第一章 质点运动学一、基本要求1．理解质点模型和参考系、惯性系的概念。

2．掌握位置矢量、位移、速度、加速度等描述质点运动和运动变化的物理量，能借助于直角坐标系和矢量三角形计算质点在平面内运动的速度和加速度。

3．掌握由运动方程求速度、加速度及由速度、加速度利用初始条件建立简单问题的运动方程。

4．掌握圆周运动的角速度和角加速度以及角量和线量的关系。

5．掌握用自然坐标系计算质点在平面内运动的速度、切向加速度和法向加速度。

6．掌握相对速度和参考系平动时的相对加速度。

7．掌握用高等数学计算运动学中的极值问题。

8．理解有运动方程推出轨道方程。

二、本章要点1．质点、参照系 忽略物体的大小和形状的理想化模型，就简化为质点。

为描述支点的运动所选取的参考物体即为参考系。

2．位置矢量 质点作机械运动时，为了确定质点在空间中的位置所引入的物理量，在直角坐标系中，位置矢量表示为k z j y i x r ++=因为式中的坐标()z y x ,,是时间的函数，所以该式又叫运动方程，由此也可得到质点的轨迹方程。

3．位移矢量和路程 质点在1t 时刻的位移为1r ，2t 时刻的位移为2r，在2t -1t 这段时间内质点的位移为 k z j y i x r r r ∆+∆+∆=-=∆12路程是质点沿轨迹走过的路径长度。

位移和路程是不同的两个概念。

4．速度和速率 速度是描写质点运动快慢程度的物理量。

dtr d v = 在直角坐标系下表示为 k dtdz j dt dy i dt dx dt r d v ++== 在自然坐标系下 τˆdtds dt ds ds r d dt r d v =⋅==其中dtds v =为质点的速率。

5．加速度 加速度是描述速度变化快慢的物理量。

22dtr d dt v d a == 在直角坐标系下表示为k a j a i a a z y x ++=其中dtx d dt dv a x x 2== dt y d dt dv a y y 2== dt z d dt dv a z z 2== 在自然坐标系下，n a a a n t ˆˆ+=τ其中：切向加速度 dt dv a t /=，是描写速度大小变化的快慢，与切向平行；法向加速度 ρ/2v a n =，是描写速度方向变化的快慢，指向曲线的曲率中心。

质点运动的基本原理与公式推导质点运动是物理学中的一个重要概念，它描述了一个点状物体在空间中的运动状态。

本文将介绍质点运动的基本原理，并通过推导公式来深入理解质点运动的规律。

一、质点运动的基本原理质点是物理学中一个理想化的概念，它假设物体在运动过程中没有形状和大小，只有质量。

因此，质点运动的基本原理可以归纳为以下几点：1. 质点的位置：质点在空间中的位置可以用矢量来表示，通常用r 表示，即r(t)，其中t表示时间。

质点的位置随时间的变化而变化，可以用函数关系式来描述。

2. 质点的速度：质点的速度指的是单位时间内质点位移的变化率。

数学上，可以用矢量v表示，即v(t) = dr(t)/dt，其中dr(t)表示质点在时间t内的微小位移。

3. 质点的加速度：质点的加速度指的是单位时间内质点速度的变化率。

数学上，可以用矢量a表示，即a(t) = dv(t)/dt，其中dv(t)表示质点在时间t内的微小速度变化。

4. 质点的运动方程：质点的运动方程是描述质点运动状态的方程。

一般情况下，可以通过质点的速度和加速度推导得出。

常见的质点运动方程有匀速直线运动方程、匀加速直线运动方程等。

二、质点运动的公式推导下面以匀速直线运动和匀加速直线运动为例，推导出相应的质点运动公式。

1. 匀速直线运动假设质点在匀速直线运动过程中，速度恒定不变，且沿着直线方向运动。

记质点的初始位置为r0，速度为v0，则质点在时间t后的位置可以表示为r(t) = r0 + v0t。

2. 匀加速直线运动假设质点在匀加速直线运动过程中，加速度恒定不变，且沿着直线方向运动。

记质点的初始位置为r0，初始速度为v0，加速度为a，则质点在时间t后的位置可以表示为r(t) = r0 + v0t + (1/2)at^2。

以上推导的公式是质点运动中常用的公式，可以帮助我们准确描述和计算质点在运动过程中的位置、速度和加速度。

结论：通过上述对质点运动的基本原理和公式推导的介绍，我们可以得出质点运动的几个重要结论：1. 质点的位置、速度和加速度都是随时间变化的量，可以用矢量表示。

20.O O O 7. O O O10. 15. O 19. 16. 11. 13. 6. 5. O O O O 22. 2. 14. O 9. 21. 18. 1. 12. 8. 17. 3. O 4. O O O 惯性直角坐标系下的牛顿质点力学经典物理认为：惯性直角坐标系有非常“特殊的地位”欧几里得立体（或简化到平面）几何，总有效。

质点系的运动学：位置（轨迹，轨道）；速度；加速度；质量rαt vαt =d r αdt a αt =d v αdt =d 2 r αdt 2mα这里的α=1,2,3...是不同质点的编号。

力：相互作用的；力场的；保守和非保守的f α,β; x ,y ,z ; =K V二体保守相互作用力：V =V r 1,2r 1,2=r1K r 2f 1=K V 1V f 2=K V 2V =K f1保守力场：每个质点都受到它的作用。

V =V rr =r =x 2C y 2C z 2f =K V上面的势可以随时间变化：V=V(t)非保守力都是耗散性的（总是伴随发热）。

如动摩擦力总力：保守的+非保守的f 总=f C f耗散牛顿运动方程：（不对α求和）m α$a α=f总α这样，如果知道了力，解方程就可以计算系统的运动了。

以上都是惯性直角坐标系下才有的东西。

也是它为何地位非常“特殊”的原因。

这套思想和方法，源自“哥白尼-笛卡尔-伽利略-开普勒-牛顿”。

（特别是他们关于天文现象的思索）我们知道，沿着这条思路的后续发展，取得了巨大成功。

但宇宙（自然界）为何是这样的？思想家和物理学者至今都“百思不解”。

无论如何，利用它们，人类可以（前所未有的）精准定量地把握自然过程。

同时发现大量“人感官不能感知”的现象。

利用实验测量和数学计算方法，极大地促进“工程-经济-军事”。

31. 28. 26. 30. 24. 47. O34. 44. 51. 43. 42.O 39. 32.O 23. O O 36. 41. 40. O 37. 45. 33. 27. 29. 38. 48. O 49. 25. O 35. 46. O 50. 故数学家也考虑这些方程的处理技术。

牛顿力学和质点的运动牛顿力学与质点运动牛顿力学简介牛顿力学是以艾萨克·牛顿命名的物理学理论体系，主要涵盖了三个运动定律，也被称为古典力学。

这三个定律构成了理解和计算物体运动的基础。

牛顿力学的适用范围是在物体运动速度远小于光速，以及物体尺度远大于原子尺度的情况下。

牛顿力学对于工程学、物理学和其他科学领域有着深远的影响。

牛顿三定律牛顿的三个运动定律分别为：1.第一定律（惯性定律）：一个物体会保持其静止状态或匀速直线运动状态，除非受到外力的作用使其改变这种状态。

2.第二定律（加速度定律）：物体的加速度与作用在它身上的外力成正比，与它的质量成反比，加速度的方向与外力的方向相同。

3.第三定律（作用与反作用定律）：任何两个物体之间的作用力和反作用力，总是大小相等、方向相反，并且作用在同一直线上。

质点运动质点是牛顿力学中一个理想化的概念，指的是一个质量可以无限集中在一个点上的物体。

在研究物体的运动时，如果物体的大小和形状对所研究的问题影响不大或者可以忽略，那么这个物体就可以被看作是一个质点。

质点运动的研究主要关注速度、加速度、位移等参数。

牛顿力学在质点运动中的应用牛顿力学中的三个定律可以用来分析和计算质点的运动。

1.第一定律与质点运动：这一定律说明了质点在没有外力作用下，或者外力合力为零的情况下，将保持原来的静止状态或者匀速直线运动状态。

这是质点运动分析中的基本假设之一。

2.第二定律与质点运动：根据这一定律，我们可以通过计算作用在质点上的外力，结合质点的质量，来确定质点的加速度。

这构成了动力学分析的核心。

公式表达为：[ F = m a ]，其中( F )是合外力，( m )是质量，( a )是加速度。

3.第三定律与质点运动：这一定律说明了作用力和反作用力之间的关系。

在质点运动中，这意味着当一个质点对另一个质点施加力时，也会受到同样大小、方向相反的力。

牛顿力学与质点运动的局限性尽管牛顿力学在解释和预测宏观物体的运动方面取得了巨大成功，但它也有局限性：1.高速运动：当物体的速度接近光速时，牛顿力学的预测将不再准确，需要使用相对论来描述。

2.1一、质点把所研究的物体视为无形状大小但有一定质量的点。

•能否看成质点依研究问题而定。

例：地球绕太阳公转:地球→质点地球半径＜＜日地距离6.4×103 km 1.5×108 km地球自转:地球≠质点•复杂物体可看成质点的组合。

二、位置矢量与运动方程1、位置矢量k z j y i x r v v v v ++=定义：从坐标原点O 指向质点位置P 的有向线段位置矢量的直角坐标分量：===++=r z r y r x z y x r γβαcos ,cos ,cos 222方向：大小：γβαP (x,y,z )r v z y xo2、运动方程k t z j t y i t x r vv v v )()()(++=矢量形式参数形式===)()()(t z z t y y t x x 3、轨道方程(轨迹)== → ===0),,(0),,()()()(z y x G z y x F t z z t y y t x x t 消去•要尽可能选择适当的参照物和坐标系，以使运动方程形式最简，从而减少计算量。

三、位移和路程O P P ’r ∆v )(t r v )(t t r ∆+v s ∆•••1、位移'()()r PP r t t r t ∆==+∆−v v v 2、路程'()()s PP s t t s t ∆==+∆−注意(1) 位移是矢量（有大小，有方向）位移不同于路程(2) 位移与参照系位置的变化无关r s ∆≠∆v 与Δr 的区别r v ∆分清O r v ∆r v∆O r∆••O PP ’r ∆v )(t r v )(t t r ∆+v s∆•••思考：什么情况下位移的大小等于路程？[例题]一质点在xOy平面内依照x= t 2 的规律沿曲线y = x3/ 320运动，求质点从第2 秒末到第4秒末的位移(式中t的单位为s；x，y的单位为cm)。

[解] ()()r r t t r t ∆=+∆−v v v 1212.6i j=+v v(cm)2121()()x x i y yj=−+−v v [()()][()()]x t t i y t t j x t i y t j =+∆++∆−+v v v v[()()][()()]x t t x t i y t t y t j=+∆−++∆−v v 66222121()()320320t t t t i j=−+−v v 662242(42)()320320i j =−+−vv 17.4 cm r ∆==v 与水平轴夹角Δarctan 46.4Δyx ϕ=o＝2.2一、速度O P P ’r∆v )(t r v )(t t r ∆+vs∆•••反映质点运动的快慢和方向的物理量1、速度的概念平均速度：平均速率:v v v v v r t r t t r t t==+−∆∆∆∆()()tt s t t s t s v ∆∆∆∆)()(−+==瞬时速度:瞬时速率:O P P ’r∆v)(t r v)(t t r ∆+vs∆•••vv v v =≠vv ,瞬时速度沿轨道切线方向2、速度的直角坐标分量()()()()::cos ,cos ,cos x y z y x z r r t x t i y t j z t kdr dx dy dz v i j k v i v j v k dt dt dt dt v v v v v v v αβγ==++==++=++ = ===v v v v vv v v v v v v v 大小方向101552r i tj t k=−++v v v v [例题]某质点的运动学方程为求：t = 0和1s 时质点的速度矢量。

质点系的功能原理基本问题有一个质点系，),,3,2,1(n i m i=。

相对于一个惯性系的直角坐标系oxyz ，质点n m m m ,,,21 于任何时刻t 的位置矢量分别为)()()()(t z k t y j t x i t r i i i i ⋅+⋅+⋅=；其中，k j i,,分别是x 轴，y 轴和z 轴正方向的单位矢量，),,3,2,1(n i =。

假设1：对于任何时刻t ，该质点系中的第i 号质点受到质点系外部的外力为)(t iF。

假设2：对于任何时刻t ，该质点系中的第j 号质点对第i 号质点的内力为)(t ij f，并不失一般性，令0)(=t iif 。

则按牛顿第二定律，有矢量方程组，式(1)。

(1) 对上述方程组分别进行“点乘”运算，得到标量方程组，式(2)。

(2) 这里tt r v i i d )(d=，对上述n 个方程进行求和得到方程，式(3)。

(3) 兹对方程式(3)积分得到方程，式(4)。

厦门大学《普通物理》课程“惯性系中的质点系功能原理”的严格推导(4) 于是得到如下定理1。

定理1：（惯性系中的质点系功能原理）)(d )(11;d )(1)()(0int 0ext 0int ext t r t ijf t t tj n i n A t v t iF t t ti n A t E t E A A i i k k∙====⋅∙===-=+⎰∑∑⎰∑这里n i v v tt r v ii i i ,,2,1;,d )(d===引理1：在“强”牛顿第三定律（大小相等，方向相反，作用在一条直线上）排斥内力吸引内力,0,0)()(,)()()()()()(<>⎩⎨⎧≡--⋅=t ij ft jift r t r t r t r t ij f t ij f i j i j的支持下，有：证明：？？？？？证明完毕。

引理2：在“刚体条件0)()(d ≡-t r t r i j”的支持下，兹由引理1得到0int ≡A从而有定理2：（惯性系中的刚体质点系功能原理） 特别地对于刚体)()(d )(100t E t E t v t iF t t ti nk k i -=⋅∙==⎰∑这里有)(211)(,)(211)(,,2,1;d )(d ,d )(d 0202t v m i nt E t v m i n t E ni tt r v t t r v i i k i i k i i i i ⋅⋅==⋅⋅=====∑∑ 刚体质点系功能原理表达完毕。

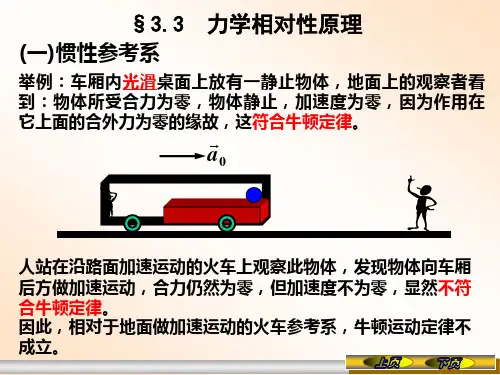
高中物理教案：探讨在不同惯性参考系下质点的运动状态转换探讨在不同惯性参考系下质点的运动状态转换引言：在物理学领域中，物体运动的研究一直都是重要的课题。

不同的动力学理论对于不同的运动状态，都会有不同的表达和处理方式。

惯性参考系是一个很重要的概念，而在不同惯性参考系下，对于质点的运动状态的转换也是一个令人困惑且难以理解的问题。

本文将从不同的角度出发，探讨在不同惯性参考系下质点的运动状态转换问题。

一、惯性参考系的概念及其特性惯性参考系是一种特殊的参考系，它具有以下三个特性：1.在惯性参考系下，任何自由粒子都是做匀速直线运动的。

2.在惯性参考系下，牛顿第一定律总是成立的。

3.任何两个相对匀速运动的惯性参考系都是等效的。

根据这些特性，我们可以用惯性参考系描述物体的运动状态，而不需要考虑其他参考系的影响。

因此惯性参考系也被称为最理想的参考系。

二、质点运动状态的转换下面我们将以基本的牛顿力学为基础，来探讨在不同惯性参考系下，质点运动状态的转换问题。

（1）惯性参考系下的运动状态转换在惯性参考系下，质点的运动状态是比较容易描述的。

根据牛顿第二定律，我们可以得到质点的运动方程。

然而，在不同的惯性参考系下，质点的运动状态并不相同。

因此，我们需要考虑如何将质点在一个惯性参考系下的运动状态转换到另一个惯性参考系下。

假设我们有两个惯性参考系K和K'，K'相对于K以速度v做匀速直线运动。

设P为质点在K系下的运动状态，P'为质点在K'系下的运动状态，t为两个系的时间差，则根据相对论的协变性原理，有如下的变换关系：x' = γ(x-vt)y' = yz' = zt' = γ(t-vx/c²)其中，γ是著名的洛伦兹因子，满足γ=1/√(1-v²/c²)，c为光速，x、y、z和x'、y'、z'、t'分别为两个惯性参考系下的运动状态坐标。

物体在惯性坐标系下的运动规律我们生活在一个以时间和空间为基准的世界，这就意味着一切物体都存在着运动。

物体的运动被科学家们归纳总结为一系列规律和定律，其中，物体在惯性坐标系下的运动规律是我们研究物理学的基石之一。

所谓惯性坐标系，是指一个相对于其他物体或者参考系没有加速度的坐标系。

在这样的坐标系下，物体的运动规律可以通过牛顿的三大运动定律进行描述。

第一定律，也称为惯性定律，表明在没有力作用下，物体将保持静止或匀速直线运动的状态。

这意味着物体会继续保持其原有的速度和方向，直到外力作用于它。

例如，当一辆汽车受到引擎的驱动力后，会开始以恒定的速度行驶，直到有其他力产生制动力或者改变方向。

第二定律是我们研究物体在惯性坐标系下运动的重要定律。

根据这个定律，物体的加速度与作用在它上面的力成正比，与物体的质量成反比。

即 F=ma，其中 F为作用在物体上的力，m 为物体的质量，a 为物体的加速度。

这个定律说明了物体的加速度与作用力的关系，也给我们描述和预测物体运动状态提供了依据。

第三定律是牛顿运动定律中的最后一条，也被称为作用力和反作用力定律。

根据这个定律，任何一个物体施加在另一个物体上的力，都会收到一个同大小、反向的力作用。

这意味着如果一个物体对另一个物体施加了一个力去推，那么它也将受到一个同样大小的力推回来。

这个定律说明了任何物体在受力的同时也会产生一个反作用力，它们始终同时存在。

同时，物体在惯性坐标系下的运动也可以通过运动学方程来进行描述。

运动学研究的是物体在不考虑作用力的情况下的运动规律。

经典的运动学方程包括位移、速度和加速度三者之间的关系。

根据运动学方程，如果我们已知物体的初始位置、初速度和运动的时间，我们可以计算出物体在惯性坐标系下的任意时刻的位置、速度和加速度。

除了牛顿运动定律和运动学方程之外，物体在惯性坐标系下的运动还受到其他因素的影响，比如空气阻力、摩擦力等。

这些因素会改变物体的运动状态和轨迹，必须进行相应的修正和计算。

牛顿运动定律与质点运动轨迹的描述牛顿运动定律是描述物体运动规律的基础理论，它提供了一种简洁而又有效的方法来描述质点的运动轨迹。

本文将探讨牛顿运动定律与质点运动轨迹的描述，并深入解析其中的物理原理。

牛顿运动定律包括三个基本原理，即惯性定律、动力定律和相互作用定律。

惯性定律指出质点在没有外力作用下会保持匀速直线运动或静止状态。

动力定律则给出了质点受力与加速度之间的关系，即F=ma，其中F是受力，m是质量，a是加速度。

相互作用定律则强调了作用力与反作用力的平衡关系。

基于这些定律，我们可以描述质点运动的轨迹。

首先，要确定质点所受的所有力，这些力可以包括重力、弹力、摩擦力等。

接下来，根据动力定律，我们可以计算出质点的加速度。

最后，借助微积分的知识，可以求取出质点在某个时间内的速度和位移，并根据这些信息绘制出质点的运动轨迹。

质点运动的轨迹可以分为三种基本类型：直线运动、曲线运动和往返运动。

对于直线运动，只需在坐标系中画出一条直线即可。

但对于曲线运动，情况就更加复杂了。

此时，我们需要根据运动方程和轨迹方程来绘制曲线。

在绘制曲线运动的轨迹时，常用到的数学工具有二阶导数、曲率和切线。

二阶导数可以帮助我们确定曲线的凹凸性，从而确定物体的加速度情况。

曲率则表示曲线的弯曲程度，而切线可以帮助我们确定物体在某一时刻的运动方向。

在现实生活中，有许多常见的运动都可以通过牛顿运动定律来描述。

例如，抛体运动是一个典型的二维曲线运动。

当我们向上扔一个物体时，物体受到重力和空气阻力的作用，从而形成了一个抛物线轨迹。

另一个例子是圆周运动，如公园里的旋转木马。

当我们坐上旋转木马时，它在保持圆周运动的同时也产生了向外的离心力，使我们产生一种向外的推力感。

总结而言，牛顿运动定律提供了一种有效的方法来描述质点运动的规律，通过分析受力、加速度以及运动方程，可以准确地绘制出质点的运动轨迹。

这些原理不仅在物理学中具有广泛的应用，也在我们日常生活中提供了一种解释和理解运动现象的框架。

物理学中的惯性和运动学惯性和运动学是物理学中非常重要的两个概念，它们对于我们理解世界的运动方式以及物体为什么会运动都有着非常重要的作用。

本文将会从不同的角度对这两个概念进行探讨，并且让大家更好的理解它们在物理学中的应用。

一、惯性惯性是指物体在没有受到力的作用下保持其原有状态的性质。

惯性是物体的属性之一，是指物体不会主动改变其状态，直到受到外界的力的作用才会发生改变。

这一概念第一次由伽利略提出，他发现，当一个物体处于匀速直线运动状态时，除了受到外界力的作用，这个物体将会一直保持其原状态。

此外，在牛顿三大定律中，惯性是第一定律，下面是这个定律的表述：“任何物体都会维持其直线运动状态，或静止状态，直到有外力作用才会改变方向和大小。

”这一定律非常重要，因为它解释了为什么我们把物体推动一段距离之后，就可以让它保持在运动状态。

因为这个物体有惯性，它会继续保持其原状态，直到受到外界的力的作用才能实现其状态改变。

二、运动学运动学是物理学中研究物体运动的学问，它的研究对象是物体的位置、速度、加速度及其变化率。

这些量都是运动物体的属性，因此运动学是描述运动物体的基本框架，是进一步研究物理学中各种现象的基础。

在运动学中，我们常常会用到以下几个概念：位移、速度、加速度。

位移：物体从一个初始位置移动到最终位置的距离称为其位移。

速度：物体在单位时间内的位移量称为其速度，速度的单位是m/s。

加速度：物体在单位时间内速度的变化量，也就是速度增加或减少的程度。

加速度的单位是 m/s²。

通过运动学中的这些基本概念，我们可以深入了解物体的运动状态，进一步分析物理学中各种现象的原因。

三、惯性与运动学的应用惯性和运动学在物理学的应用中有着非常重要的地位。

比如在工业生产中，我们需要检查某个机器是否存在问题，一般的方法是通过检查物体的运动状态来判断，如果物体的运动过程中出现不合理的偏差，那么就说明这个机器存在问题。

此外，在交通运输系统中，我们也需要了解物体的惯性和运动学来预测其运动状态，比如在行车过程中，若车辆想要急刹车则由于该车具有惯性，会出现刹车前状态并未发生改变，导致刹车效果不理想的情况。