第二章 惯性系下质点运动学

《力学》课程教学大纲一、课程基本信息英文名称 Mechanics 课程代码 PHYS1001课程性质 大类基础课程 授课对象 物理学学 分 4学分 学 时 72学时主讲教师 修订日期 2021年9月指定教材 张汉壮. 力学（第四版）高等教育出版社, 2019.二、课程目标（一）总体目标：通过力学课程的学习，使学生能够系统的掌握力学的基础知识，掌握力学基础的研究方法；在获取知识的同时，对简化模型的选取、量纲分析、数量级估计与定量计算的能力、提出问题和分析问题的能力、理论联系实际的能力等都应有所提高和发展。

适当的为物理学的前沿打开窗口，开阔学生的眼界、启迪并激发学生的探索和创新精神，更深层次地提升其科学素质。

（二）课程目标：课程目标1：使学生理解物理学的思想和研究问题的方法，培养其独立思考问题的能力和创新能力；使学生理解力与运动之间的关系，掌握力学的基本概念，基本定律和基本原理，能较为灵活地加以运用；为学生后继专业基础课程，例如光学、电磁学、理论力学等课程的学习及进一步获取有关知识奠定必要的物理基础。

课程目标2：系统的掌握力学的基础知识和研究方法，获取知识的同时，对简化模型的选取、量纲分析、数量级估计与定量计算的能力、提出问题和分析问题的能力、理论联系实际的能力等都应有所提高和发展，并进一步根据实际的物理运动过程构建模型，解决实际问题，综合提高学生的科学素养。

课程目标3：回顾力学发展史，了解一门学科发展过程中科学家所做贡献和其展现的科学精神；介绍物理学的前沿知识，适当引入新中国在工程建设、航天航空等方面取得的一系列成就，开阔学生的眼界、启迪并激发学生的探索和创新精神，更深层次地提升其科学素质的同时培养学生的爱国情怀。

使学生了解人类文明发展的现状是人才素质培养的一个重要方面。

（三）课程目标与毕业要求、课程内容的对应关系表1：课程目标与课程内容、毕业要求的对应关系表课程目标对应课程内容对应毕业要求（及对应关系说明）课程目标1 第O章 绪论第一章 质点运动学第二章 惯性系下质点动力学第三章 非惯性系下质点动力学第四章 动量定理与动量守恒定律第五章 功能原理与机械能守恒定律第六章 角动量定理与角动量守恒定律第七章 刚体第八章 流体第九章 振动第十章 波动2-2 掌握物理知识和物理方法，能应用物理知识和方法描述自然现象和规律2-3 掌握物理学理论知识，能解释或理解自然现象和自然规律，具有初步解决科学问题的能力7-1 能够运用各类搜索工具搜索网络信息和文献资料能规范撰写物理相关领域或课题进展调研报告系统掌握力学的基础知识，掌握力学基础的研究方法。

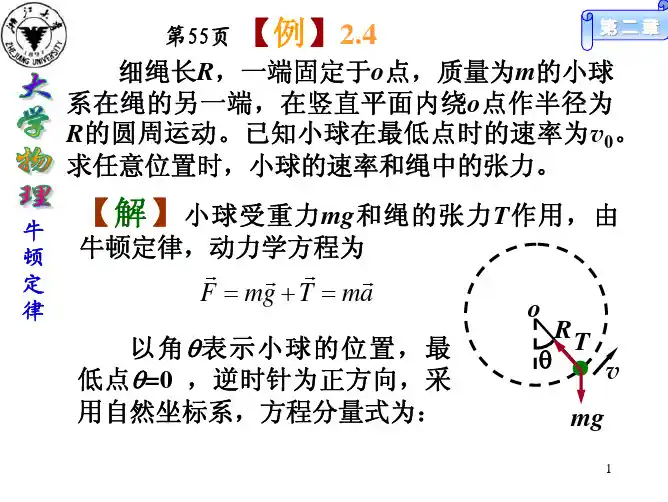
矢量式运动函数直角坐标系极坐标系自然坐标系d s R d v Rd t d tθω===t dv a R dtα==22n v a RR==ω2.1 牛顿运动定律惯性力实用的惯性系：地面系：坐标轴固定在地面上—赤道处自转加速度a ~0.034 m/s2。

是一个较好的惯性系。

地心系：地心为原点，坐标轴指向恒星—绕太阳公转的向心加速度～6×10-3m/s2（g的10－3）。

是个更好的惯性系太阳系：太阳中心为原点，坐标轴指向恒星—绕银河中心的向心加速度～1.8×10-10m/s2。

是一个更加好的惯性系FK4系：是以选定的1535颗恒星平均静止位形作为基准的参考系。

目前最好的惯性系。

牛顿定律应用举例两类问题：已知力求运动；已知运动求力。

解题思路：确定研究对象；受力分析；建立坐标系分析运动情况；列方程求解；检验结果（量纲？特例？等）；2−GTθcos=GTcos=−θm1g-T=m1a1fμ-m2g=m2a2=m2(a1-a)m 1g-T=m 1a 1f μ-m 2g=m 2a 2=m 2(a 1-a)T= f μ212211)(m m a m g m m a ++−=211212)(m m a m g m m a +−−=2121)2(m m m m a g f T −==µN’>mg称超重N’<mg称失重由于地球的自转，地面参考系是一个转动参考系，在地面参考系中就能观察到科里奥利现象强热带风暴旋涡傅科摆摆面的旋转1851年傅科在巴黎（北半球）的一个大厅里悬挂摆长67 米的摆。

发现摆动平面每小时沿顺时针方向转过11ο15’角度。

北西东南离心力抵消, 也出现完全失重状态。

* 潮汐现象潮汐是海水的周期性涨落现象，一天两次涨潮。

“昼涨称潮，夜涨称汐”。

潮汐是月亮、太阳对海水的引力以及地球公转和自转的结果。

根据定量计算（略），月亮引潮力是太阳的2 倍多。

所以，潮汐主要是由月球引力引起！引潮力不仅作用在流体上，它对固体也有作用，使固体发生微小的形变。

第二章习题答案2.1.1 质点的运动学方程为j t i t r j i t r ˆ)14(ˆ)32()2(ˆ5ˆ)23()1(-+-=++=求质点的轨迹并用图表示解：（1）⎭⎬⎫=+=523y t x 平行于x 轴的直线：y=5(2)⎭⎬⎫-=-=1432t y t x 消去t 的轨迹方程：0534=-+y x2.1.2 质点的运动学方程为kj e i e r t t ˆ2ˆˆ22++=-。

(1)求质点的轨迹。

（2）求自t = -1 至t = 1质点的位移解：（1）由运动方程得质点轨迹的参数方程为 )3()2()1(222⎪⎩⎪⎨⎧===-z ey e x tt （1）x （2）消去t ，得轨迹方程 ⎩⎨⎧==21z xy（2）自t = -1 至t = 1质点的位移：je e i e e r r r k j e i e r k j e i e r t t ˆ)(ˆ)(ˆ2ˆˆˆ2ˆˆ,1,1222211221221-------+-=-=∆++=++==-= 2.1.3 质点的运动学方程为j t i t r ˆ)32(ˆ42++=。

（1）求质点的轨迹；（2）求自t=0至t=1质点的位移解：由质点的运动方程⎩⎨⎧+==)2(32)1(42t y t x （1） 质点的轨迹：消去t 得：2)3(-=y x（2） 位移：ji r r r j i r j r t t ˆ2ˆ4ˆ5ˆ4ˆ3101221+=-=∆+====2.2.1 雷达站于某瞬时测得飞机位置为R 1=4100m ，θ1=33.70，0.75s 后测得R 2=4240m ，θ2=29.30，R 1,R 2均在铅直平面内，求飞机瞬时速度的近似值和飞行方向（α角）。

解：取雷达站位置为原点，飞机在两个时刻的位置矢量分别为r 1和r 2，则| r 1|=R 1, | r 2|=R 2，如图所示由余弦定理，在0.75s 时间间隔内飞机的位移的大小为mR R R R r r r r r 4.349)3.297.33cos(42404100242404100)cos(2)cos(200222121222121212221≈-⨯⨯-+=--+=--+=∆θθθθ飞机的瞬时速度的大小：==∆∆≈smt r v 75.04.349465.8m/s飞机的瞬时速度方向：由正弦定理)3.297.33sin(4.349sin 4240)sin(sin 00212-=⇒-∆=γθθγr r100001207.341806.11193.0arcsin 18090,93.04.4sin 4.3494240sin ≈--=∴≈-=∴>∴>≈=γθαγγγr r另解：利用矢量在直角坐标系中的正交分解. 选平面直角坐标系,取雷达站的位置为坐标原点,x 轴沿水平方向,y 轴铅直向上,则在两个时刻飞机的位置矢量分别可表示为ji j i jR i R r ji j i jR i R r ˆ98.2074ˆ57.3697ˆ3.29sin 4240ˆ3.29cos 4240ˆsin ˆcos ˆ86.2274ˆ01.3411ˆ7.33sin 4100ˆ7.33cos 4100ˆsin ˆcos 00222220011111+=⨯+⨯=+=+=⨯+⨯=+=θθθθ 飞机飞行0.75s 后的位移矢量为j i r r r ˆ88.199ˆ56.28612-=-=∆飞机瞬时速度的大小的近似值:s m t rv /8.46575.038.34975.088.19956.28622=≅+=∆∆≈飞机瞬时速度的方向与x 轴的夹角:09.3482.038.34956.286ˆcos =∴==∆⋅∆=ααr i r2.2.2 一圆柱体沿抛物线轨道运动.抛物线的轨道方程为y=x 2/200(长度:mm).第一次观测到圆柱体在x=249mm 处,经过时间2ms 后圆柱体移到x=234mm 处.求圆柱体瞬时速度的近似解：第一次观测时，x=249mm, y=x 2/200=(249)2/200≈310mm ，j i r ˆ310ˆ2491+=2ms 后，x=234mm, y=x 2/200=(234)2/200≈273.78mm ，j i r ˆ78.273ˆ2342+=圆柱体的位移：mm r j i r r r 2.3922.3615ˆ22.36ˆ152212≈+=∆--=-=∆∴ms mm msmm t r v /6.1922.39==∆∆≈速度与x 轴的夹角：5.112383.02.3915ˆcos -≈∴-≈-=∆⋅∆=ααr i r2.2.3 一人在北京音乐厅内听音乐，离演奏着17m 。

2.1一、质点把所研究的物体视为无形状大小但有一定质量的点。

•能否看成质点依研究问题而定。

例：地球绕太阳公转:地球→质点地球半径＜＜日地距离6.4×103 km 1.5×108 km地球自转:地球≠质点•复杂物体可看成质点的组合。

二、位置矢量与运动方程1、位置矢量k z j y i x r v v v v ++=定义：从坐标原点O 指向质点位置P 的有向线段位置矢量的直角坐标分量：===++=r z r y r x z y x r γβαcos ,cos ,cos 222方向：大小：γβαP (x,y,z )r v z y xo2、运动方程k t z j t y i t x r vv v v )()()(++=矢量形式参数形式===)()()(t z z t y y t x x 3、轨道方程(轨迹)== → ===0),,(0),,()()()(z y x G z y x F t z z t y y t x x t 消去•要尽可能选择适当的参照物和坐标系，以使运动方程形式最简，从而减少计算量。

三、位移和路程O P P ’r ∆v )(t r v )(t t r ∆+v s ∆•••1、位移'()()r PP r t t r t ∆==+∆−v v v 2、路程'()()s PP s t t s t ∆==+∆−注意(1) 位移是矢量（有大小，有方向）位移不同于路程(2) 位移与参照系位置的变化无关r s ∆≠∆v 与Δr 的区别r v ∆分清O r v ∆r v∆O r∆••O PP ’r ∆v )(t r v )(t t r ∆+v s∆•••思考：什么情况下位移的大小等于路程？[例题]一质点在xOy平面内依照x= t 2 的规律沿曲线y = x3/ 320运动，求质点从第2 秒末到第4秒末的位移(式中t的单位为s；x，y的单位为cm)。

[解] ()()r r t t r t ∆=+∆−v v v 1212.6i j=+v v(cm)2121()()x x i y yj=−+−v v [()()][()()]x t t i y t t j x t i y t j =+∆++∆−+v v v v[()()][()()]x t t x t i y t t y t j=+∆−++∆−v v 66222121()()320320t t t t i j=−+−v v 662242(42)()320320i j =−+−vv 17.4 cm r ∆==v 与水平轴夹角Δarctan 46.4Δyx ϕ=o＝2.2一、速度O P P ’r∆v )(t r v )(t t r ∆+vs∆•••反映质点运动的快慢和方向的物理量1、速度的概念平均速度：平均速率:v v v v v r t r t t r t t==+−∆∆∆∆()()tt s t t s t s v ∆∆∆∆)()(−+==瞬时速度:瞬时速率:O P P ’r∆v)(t r v)(t t r ∆+vs∆•••vv v v =≠vv ,瞬时速度沿轨道切线方向2、速度的直角坐标分量()()()()::cos ,cos ,cos x y z y x z r r t x t i y t j z t kdr dx dy dz v i j k v i v j v k dt dt dt dt v v v v v v v αβγ==++==++=++ = ===v v v v vv v v v v v v v 大小方向101552r i tj t k=−++v v v v [例题]某质点的运动学方程为求：t = 0和1s 时质点的速度矢量。

质点系的功能原理基本问题有一个质点系，),,3,2,1(n i m i=。

相对于一个惯性系的直角坐标系oxyz ，质点n m m m ,,,21 于任何时刻t 的位置矢量分别为)()()()(t z k t y j t x i t r i i i i ⋅+⋅+⋅=；其中，k j i,,分别是x 轴，y 轴和z 轴正方向的单位矢量，),,3,2,1(n i =。

假设1：对于任何时刻t ，该质点系中的第i 号质点受到质点系外部的外力为)(t iF。

假设2：对于任何时刻t ，该质点系中的第j 号质点对第i 号质点的内力为)(t ij f，并不失一般性，令0)(=t iif 。

则按牛顿第二定律，有矢量方程组，式(1)。

(1) 对上述方程组分别进行“点乘”运算，得到标量方程组，式(2)。

(2) 这里tt r v i i d )(d=，对上述n 个方程进行求和得到方程，式(3)。

(3) 兹对方程式(3)积分得到方程，式(4)。

厦门大学《普通物理》课程“惯性系中的质点系功能原理”的严格推导(4) 于是得到如下定理1。

定理1：（惯性系中的质点系功能原理）)(d )(11;d )(1)()(0int 0ext 0int ext t r t ijf t t tj n i n A t v t iF t t ti n A t E t E A A i i k k∙====⋅∙===-=+⎰∑∑⎰∑这里n i v v tt r v ii i i ,,2,1;,d )(d===引理1：在“强”牛顿第三定律（大小相等，方向相反，作用在一条直线上）排斥内力吸引内力,0,0)()(,)()()()()()(<>⎩⎨⎧≡--⋅=t ij ft jift r t r t r t r t ij f t ij f i j i j的支持下，有：证明：？？？？？证明完毕。

引理2：在“刚体条件0)()(d ≡-t r t r i j”的支持下，兹由引理1得到0int ≡A从而有定理2：（惯性系中的刚体质点系功能原理） 特别地对于刚体)()(d )(100t E t E t v t iF t t ti nk k i -=⋅∙==⎰∑这里有)(211)(,)(211)(,,2,1;d )(d ,d )(d 0202t v m i nt E t v m i n t E ni tt r v t t r v i i k i i k i i i i ⋅⋅==⋅⋅=====∑∑ 刚体质点系功能原理表达完毕。