大偏心受压柱汇总

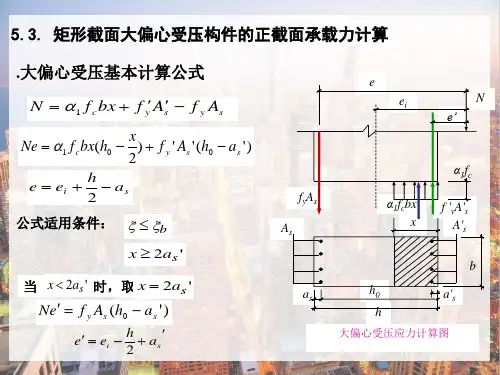
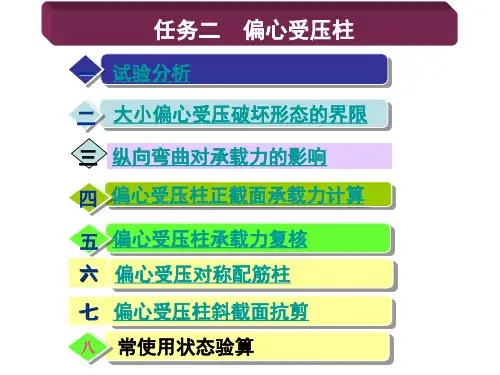
偏心受压构件一、偏心受压构件包括大偏心受压和小偏心受压两种情况，无论是大偏心受压还是小偏心受压均要考虑偏心距增大系数η。

2012.11400i l e h h ξξη⎛⎫=+ ⎪⎝⎭10.5.c f A Nξ=02 1.150.01l hξ=-此公式中要注意如下几点：①h ——截面高度。

环形截面取外直径；圆形截面取直径。

②0h ——截面有效高度。

对环形截面取02s h r r =+；对圆形截面取0s h r r =+。

r 、2r 、s r 按《混凝土结构设计规范》第7.3.7条和7.3.8条取用。

③A ——构件的截面面积。

对T 形截面和工形截面，均取()''.2.f fA b h b b h =+-④1ξ——偏心受压构件的截面曲率修正系数，当1 1.0ξ>取1 1.0ξ=； 2ξ——构件长细比对截面曲率的影响系数，当015l h<时，取2 1.0ξ=；⑤当偏心受压构件的长细比017.5l i ≤（或05l h≤）时，可直接取 1.0η=。

注意：017.5l i≤与05l h≤基本上是等价的。

准确地说是0 5.05l h≤二、两种破坏形态的含义截面进入破坏阶段时，离轴向力较远一侧的纵向钢筋受拉屈服，截面产生较大的转动，当截面受压区边缘的混凝土压应变达到其极值后，混凝土被压碎，截面破坏。

截面进入破坏阶段后，离轴向力较远一侧的纵向钢筋或者受拉或者受压但始终不屈服，截面转动较小，当截面受压区边缘的混凝土压应变达到其极限值后，混凝土被压碎，截面破坏 。

两种破坏形态的相同点：截面最终破坏都是由于受压区边缘混凝土被压碎而产生的，并且离轴向力较近一侧的钢筋（或曰受压钢筋's A ）都受压屈服。

两种破坏形态的不同点：起因不同。

大偏心受压破坏的起因是离轴向力较远一侧的钢筋（或曰受拉钢筋s A ）受拉屈服；而小偏心受压破坏则是由于截面受压区边缘混凝土压应变接近其极值。

所以大偏心受压破坏也被称为“受拉破坏”——延性破坏；小偏心受压破坏也被称为“受压破坏”——脆性破坏。

钢筋混凝土受压柱大小偏心判断方法的讨论王中发【摘要】本文就钢筋混凝土受压柱的受力特点进行探讨，以探寻更有效的大小偏心判断方法。

%This paper discusses the mechanical characteristics of reinforced concrete compression column to explore more effective method to determine the size of the eccentric.【期刊名称】《价值工程》【年(卷),期】2015(000)003【总页数】2页(P128-129)【关键词】钢筋混凝土;偏心受压柱;承载力计算;判断【作者】王中发【作者单位】湖北水利水电职业技术学院水利建筑工程系，武汉430070【正文语种】中文【中图分类】U441钢筋混凝土偏心受压柱根据破坏时的特征分为大偏心受压和小偏心受压，其区别在于远离偏心压力一侧的纵向受力钢筋在柱发生破坏时是否达到屈服强度（即该侧纵筋的应力σx=fy）。

《混凝土结构设计规范》（GB50010-2011）给出的判断条件为：当满足x≤h0ξb或ξ≤ξb的条件时，受压柱为大偏心受压，反之为小偏心受压。

但在进行柱的设计时，通常柱两侧的纵向受力钢筋是未知的，也就无法直接计算x或ξ，也就无法直接判断要设计的柱是大偏心还是小偏心，因大小偏心的承载力计算公式不同，导致设计计算无法进行。

钢筋混凝土受压柱大小偏心判断方法如下：《混凝土结构设计规范》给出的偏心受压柱正截面承载力计算公式如下：①对于对称配筋，比较好判断。

先假定为大偏心受压（σx=fy），根据公式（1）取极限状态，公式按等号计算，计算出，然后根据x和ξbh0的大小关系判断。

若x≤h0ξb则表明假设正确，确为大偏心受压，反之为小偏心受压。

②对于非对称配筋，由于无法直接计算出受压区计算高度x，上述方法就不再适用了，需要另外的方法，本文重点讨论这个问题。

偏心受压混凝土柱受力性能的研究偏心受压混凝土柱的受力性能一直是土木工程师和研究人员们关注的焦点。

由于其具有许多优良的性能，如高承载能力、抗震性、耐久性等，使其成为了现代建筑中不可或缺的构件之一。

本文将探讨偏心受压混凝土柱的受力性能以及当前的研究现状和趋势。

一、偏心受压混凝土柱的概念偏心受压混凝土柱是指在单轴受力条件下，柱子轴线和荷载作用线不在同一平面内，因此在柱子承受荷载的时候，其受力状态相对于直接受力的柱子受到了一定的变化，这种变化会在某些情况下对其受力性能产生一定影响。

因此，偏心受压混凝土柱的研究对于工程的设计和实际应用具有重要意义。

二、偏心受压混凝土柱的受力性能1.受力状态由于偏心受压混凝土柱的受力状态发生了变化，其承受荷载时存在两种可能的失稳模式：轴向压缩失稳和侧向扭转失稳。

在轴向压缩失稳的情况下，柱子将会沿着轴向坍塌，而在侧向扭转失稳的情况下，柱子就会发生旋转，最终失稳。

2.承载能力偏心受压混凝土柱的承载能力与其几何形状、材料性能和荷载条件等因素有关。

一般来说，柱子的截面越大、材料强度越高，则其承载能力也就越大。

此外，荷载的位置也对其承载能力产生一定的影响。

当荷载点处于柱子中心时，其承载能力最大；而当荷载点偏离柱子中心时，其承载能力则会有所降低。

3.抗震性由于偏心受压混凝土柱的受力状态相对于直接受力的柱子有所不同，因此其抗震性能也存在一定差异。

具体来说，偏心受压混凝土柱的抗震性能被认为受其偏心距离、柱子截面形状和荷载作用位置等因素的影响。

因此，在实际工程中，应结合具体情况进行抗震设计。

三、偏心受压混凝土柱的研究现状和趋势目前，关于偏心受压混凝土柱的研究多集中在其承载能力和抗震性能方面。

随着大量的理论研究和实验室试验，人们逐渐对偏心受压混凝土柱的受力性能有了更深入的认识。

现在，人们开始将关注点转移到如何更好地优化偏心受压混凝土柱的设计和施工方案上。

例如，通过改变柱子的几何形状、材料特性，优化荷载分配方式等手段，来提高其承载能力和抗震性能。

大偏压与小偏压解决方案比较偏心受压构件正截面承载力计算一、偏心受压构件正截面的破坏特征（一）破坏类型1、受拉破坏：当偏心距较大，且受拉钢筋配置得不太多时，发生的破坏属大偏压破坏。

这种破坏特点是受拉区、受压区的钢筋都能达到屈服，受压区的混凝土也能达到极限压应变，如图7—2a 所示。

2、受压破坏：当偏心距较小或很小时，或者虽然相对偏心距较大，但此时配置了很多的受拉钢筋时，发生的破坏属小偏压破坏。

这种破坏特点是，靠近纵向力那一端的钢筋能达到屈服，混凝土被压碎，而远离纵向力那一端的钢筋不管是受拉还是受压，一般情况下达不到屈服。

（二）界限破坏及大小偏心受压的分界1、界限破坏在大偏心受压破坏和小偏心受压破坏之间，从理论上考虑存在一种“界限破坏”状态；当受拉区的受拉钢筋达到屈服时，受压区边缘混凝土的压应变刚好达到极限压应变值。

这种特殊状态可作为区分大小偏压的界限。

二者本质区别在于受拉区的钢筋是否屈服。

2、大小偏心受压的分界由于大偏心受压与受弯构件的适筋梁破坏特征类同,因此,也可用相对受压区高度比值大小来判别。

当时，截面属于大偏压；当时,截面属于小偏压;当时，截面处于界限状态。

二、偏心受压构件正截面承载力计算（一）矩形截面非对称配筋构件正截面承载力1、基本计算公式及适用条件：(1)大偏压（）：，（7-3），（7-4）（7-5）注意式中各符号的含义。

公式的适用条件：（7-6）（7-7）界限情况下的：（7-8）当截面尺寸、配筋面积和材料强度为已知时，为定值，按式（7-8）确定。

(2)小偏压（）：（7-9）（7-10）式中根据实测结果可近似按下式计算：（7-11）注意：﹡基本公式中条件满足时，才能保证受压钢筋达到屈服。

当时，受压钢筋达不到屈服，其正截面的承载力按下式计算。

（7-12）为轴向压力作用点到受压纵向钢筋合力点的距离，计算中应计入偏心距增大系数。

﹡﹡矩形截面非对称配筋的小偏心受压构件，当N >f c bh时，尚应按下列公式验算：（7-13）（7-14）式中，——轴向压力作用点到受压区纵向钢筋合力点的距离；——纵向受压钢筋合力点到截面远边的距离；2、垂直于弯矩作用平面的受压承载力验算当轴向压力设计值N较大且弯矩作用平面内的偏心距较小时，若垂直于弯矩作用平面的长细比较大或边长较小时，则有可能由垂直于弯矩作用平面的轴心受压承载力起控制作用。

钢筋混凝土受压柱大小偏心判断方法的讨论前言在钢筋混凝土结构中，柱子是承受垂直荷载并将其传递到地面的重要部分。

然而，当柱子承受侧向荷载时，就会发生大小偏心。

为了保证结构的稳定和安全，我们需要判断钢筋混凝土受压柱的大小偏心是否超过规定的极限值。

本文将讨论钢筋混凝土受压柱大小偏心判断方法。

钢筋混凝土受压柱的大小偏心在钢筋混凝土结构中，柱子往往不仅承受垂直荷载，还会承受侧向荷载。

当侧向荷载产生时，柱子会出现大小偏心。

大小偏心是指柱子中心线和荷载中心线之间的距离，如果这个距离超过规定的极限值，就会影响钢筋混凝土结构的安全性。

判断大小偏心的方法直接验算法直接验算法是最常用的方法之一。

它是通过计算柱子截面的面积和惯性矩，进而计算得出柱子截面受到侧向荷载时的最大偏心距离。

如果最大偏心距离小于规定的极限值，柱子就是安全的。

简化验算法简化验算法是一种较为简便的方法。

它是通过假设柱子承受侧向荷载时最大偏心距离就等于钢筋混凝土受压区的中心偏离柱中心的距离，从而进行判断。

如果计算的结果小于规定的极限值，柱子就是安全的。

试重法试重法也是一种常用的方法，它是通过施加不同的试重，测量柱子变形量来判断其大小偏心是否超过规定的极限值。

试重法需要考虑试重操作的难度以及试重过程中可能带来的损坏问题。

向弯性转化法向弯性转化法是通过将柱子转化为等效的弯曲柱或悬臂梁来进行判断。

该方法需要计算柱子的弯曲强度，以及相应的弯曲应力和偏心距离。

如果计算的结果小于规定的极限值，柱子就是安全的。

总结钢筋混凝土受压柱的大小偏心是影响结构安全性的重要因素。

我们可以采用直接验算法、简化验算法、试重法或者向弯性转化法来进行判断。

不同的判断方法有各自的优缺点，需要根据具体情况进行选择。

为了保证结构的稳定和安全，我们必须认真进行大小偏心的判断和设计。

大偏心受压构件承载力计算公式根据大偏心受压破坏时的截面应力图形和基本假定，简化出大偏心受压柱的承载力计算简图。

靠近轴向压力一侧的纵向钢筋截面面积为A s′（简称为近侧钢筋），远离轴向压力一侧的纵向钢筋截面面积为A s（简称为远侧钢筋）。

（a）纵剖面（b）横剖面矩形截面大偏心受压柱正截面受压承载力计算简图根据承载力计算简图及截面内力平衡条件，并满足承载能力极限状态设计表达式的要求，可建立如下基本公式：KN≤f c bx + f y′A s′–f y A sKNe≤f c bx（h0–）+f y′A s′（h0–a s′）式中e——轴向压力作用点至远侧钢筋A s合力点之间的距离（mm），e = ηe0+h/2–a s；e0——轴向压力对截面重心的偏心距（mm），e0=M/N；η——轴向压力偏心距增大系数，；a s——远侧钢筋A s合力点至截面近边缘的距离（mm）；a s′——近侧钢筋A s′合力点至截面近边缘的距离（mm）；h0′——纵向受压钢筋合力点至受拉边或受压较小边的距离（mm），h0′= h –a s′。

将x=ξh0代入基本公式中，并令αs=ξ（1–ξ），则可得出KN≤f c bξ h0 + f y′A s′–f y A s KNe≤αs f c bh02+f y′A s′（h0–a s′）基本公式应满足下列适用条件：（1）为了保证构件破坏时远侧受拉钢筋应力能达到屈服强度，应满足：x≤ξb h0或ξ≤ξb（2）为了保证构件破坏时，近侧受压钢筋应力能达到屈服强度，应满足：x≥2a s′当x＜2a s′时，近侧受压钢筋的应力达不到f y′，截面承载力可按下式计算：KNe′≤f y A s（h0–a s′）式中e′——轴向压力作用点至近侧钢筋A s′合力点的距离（mm），e′=ηe0–h/2+a s′。

大偏心受压构件的名词解释大偏心受压构件是指在受压状态下，构件的压力作用点偏离截面中心轴较大的构件。

它广泛应用于建筑和工程领域，例如桥梁、支架、柱子等。

在这些结构中，大偏心受压构件承受着巨大的力量，因此对其进行适当的定义和解释非常重要。

首先，大偏心受压构件的核心概念是“偏心”。

偏心是指受力作用点与截面中心轴之间的水平距离。

在大偏心受压构件中，这个偏心距离相对较大，使得力的作用点远离截面的中心。

这种偏心距离将导致构件发生弯曲和扭转的变形，同样也会给构件带来剪切力、压力和弯矩等多种力的作用。

大偏心受压构件的设计和分析需要考虑多个因素，其中之一是构件的几何形状。

常见的大偏心受压构件通常为矩形或方形的柱子或梁。

其次，材料的选择也是设计过程中需要考虑的重要因素。

通常情况下，大偏心受压构件往往使用高强度和高刚度的材料，以保证其能够承受较大的力和变形。

在分析大偏心受压构件时，需要考虑其构件行为的不同阶段。

首先是初始阶段，在这个阶段内，构件承受的力较小，变形也相对较小。

但是，随着受力的增加，构件将逐渐进入非线性阶段，这会导致构件的变形增加并逐渐失去稳定性。

这是设计中需要特别关注的阶段，因为结构的破坏可能发生在这个时候。

大偏心受压构件的抗压承载力可以通过多种方法进行计算。

常用的方法有基于材料的强度和刚度，以及基于构件的受力分析和弹塑性原理。

对于大多数实际工程应用，采用更为精确的有限元分析方法来进行计算和验证承载力是常见的做法。

此外，在实际应用中，大偏心受压构件的设计还需要考虑到工作条件和先进的施工技术。

这些因素将对构件的使用寿命、安全性和可持续性产生重要影响。

综上所述，大偏心受压构件是一种在受压状态下，其压力作用点偏离截面中心轴较大的构件。

它的设计和分析需要考虑多个因素，包括构件的几何形状、材料的选择以及构件的行为和承载力计算。

通过了解和理解大偏心受压构件，我们能够更好地应用和设计这些构件，保证其安全性和性能，推动建筑和工程行业的发展。

对称配筋的大偏心受压构件与小偏心受压构件的计算我们平时在讲结构设计的时候，常听到“对称配筋的大偏心受压构件”和“小偏心受压构件”，说实话，这听上去有点复杂，但一旦搞明白了，你就会发现其实也没那么难。

其实就是讲一个结构在受力时，钢筋怎么安排，以及它受力的状态是什么样的。

大家可以想象一下，你平时坐在椅子上，如果椅子的腿不均匀，或者一侧的腿偏短，你坐上去肯定不稳吧？这其实和我们设计结构时考虑的“偏心”是类似的。

大偏心受压就是钢筋没在柱子的中间，而是在一边，受力就像椅子不平稳一样，压力集中，容易发生倾斜、破坏。

小偏心受压嘛，钢筋虽然不在正中间，但差距不大，影响就小多了。

咱们得聊聊这“大偏心”和“小偏心”到底是啥意思。

你可以把“大偏心”想象成一个人踩在不平的地面上，感觉全身都在晃动，左右不稳，受力点偏移很多，根本没法保证力均匀分布；而“小偏心”就好比踩在稍微不平的地上，虽然也有点倾斜，但比起大偏心，那简直是“小巫见大巫”了，受力分布还是能保持一定的均衡。

所以，大偏心受压构件的计算要考虑的因素更多，稍微马虎就会出现危险；而小偏心的情况，设计时稍微一调整，基本能保持稳定。

说到这里，咱们再聊聊这“对称配筋”是怎么回事。

其实就是指钢筋布置要对称，像你买衣服一样，左边右边得一样，穿着才不丑。

这个对称，能帮助结构更好地分担负荷，像你抬个重东西，左右手得均衡，才不会单侧负担太重，导致受伤。

同样的道理，如果钢筋布置不对称，受力点偏了，整个结构的稳定性就成了问题。

特别是对于大偏心受压构件，如果钢筋配得不对称，问题就会更加突出，甚至会导致整个构件崩溃。

想象一下，你拿着一个碗，一边放得不稳，结果一碰就翻了，摔得稀巴烂。

但是，咱们也不能光说问题，咱们得知道怎么解决。

说白了，结构设计就是要在考虑负荷、尺寸、材质等各种条件下，找到一个最佳的解决方案。

对于大偏心受压构件，我们得特别注意钢筋的分布和数量，不能随便糊弄。

比如，钢筋的位置就得更加靠近受压侧，要确保在结构受压时，力能够顺畅传递，防止钢筋因为受力过大而发生断裂。