当前位置：文档之家 › 第8章 数学形态学及其应用

第8章 数学形态学及其应用

  • 格式：ppt
  • 大小：4.28 MB
  • 文档页数：100

下载文档原格式

  / 100

合集下载

数学形态学

数学形态学

数学形态学
数学形态学是一种新兴的研究领域，它旨在分析几何图形的结构，形状和功能之间的关系。

它的研究，使用广义的概念，为许多不同的问题提供解决方案，其中包括拓扑、图像处理、科学可视化、结构生物学和信号处理等。

数学形态学是一个综合性的学科，它运用多种数学工具和科学原理来描述和分析图形学中出现的复杂形状，是形状和几何的综合科学。

它的本质是把复杂的形状分解成不同的形状元素，再利用数学中的手段将这些元素组合起来，以描述和揭示形状结构之间的联系。

数学形态学是一门基于计算机的学科，它使用计算机技术，通过对几何图形和形状的像素分析，捕捉形状中各种特征，分析不同形状间的关系，建立并匹配形状，以及重建和综合形状信息。

同时，它也旨在将计算机技术与形状分析结合起来，用于解决计算机的实际应用问题，如机器视觉和图像处理。

数学形态学广泛地应用于各种领域，如机器人系统，空间科学，图形学，地理和空间信息，甚至分子生物学等。

它还可以用于将几何图形可视化，以及应用于工程设计，以更直观的方式表示几何形状，并为设计者和设计家提供视觉上的参考。

数学形态学的研究不仅仅局限于几何图形，同时也研究自然现象中出现的结构，并尝试描述和表述自然界中出现的复杂形状。

从自然现象中抽象出来的形状，往往能够帮助科学家们更好地理解现象，并最终基于研究结果，为实际应用研发有效的算法或具备一定属性的形
状。

总的来说，数学形态学是一种立足于数学的研究领域，它涉及到多层次的形状分析，以及形状和空间之间的关系，研究和分析丰富多彩的形状属性。

它旨在更好地理解形状，并为许多实际问题提供解决方案，同时也为计算机视觉和机器人系统提供支撑及应用。

数学形态学及其应用

数学形态学及其应用

数学形态学及其应用数学形态学及其应用数学形态学是一种数学方法和理论，最早由法国数学家乌戈尔·乔尔丹（Ugo Cerletti）在20世纪60年代提出。

它基于拓扑学、代数学和概率论等学科的基本原理，研究对象是图像和信号等离散数据的形状和结构，并利用数学统计的方法对它们进行分析和处理。

随着计算机技术的发展和应用需求的增加，数学形态学已经成为图像处理、模式识别和计算机视觉等领域中的重要工具。

数学形态学的基本概念包括结构元素、腐蚀、膨胀、开运算和闭运算等。

结构元素是一个小的图像或信号，用来描述和刻画对象的特征。

腐蚀和膨胀是两种基本的形态学操作，它们可以对图像或信号进行形状的变化和结构的调整。

开运算和闭运算是由腐蚀和膨胀组合而成的操作，用来改善图像的质量和特征。

在数学形态学的基础上，还发展了很多衍生的操作和算法，如基本重建、灰度形态学和形态学滤波等。

数学形态学在图像处理中的应用非常广泛。

例如，在图像分割中，可以利用数学形态学的方法提取目标的边界和内部结构；在图像增强中，可以利用形态学处理方法去除图像中的噪声和不规则部分；在模式识别中，可以利用形态学算法提取和描述对象的特征；在计算机视觉中，可以利用形态学方法实现图像的匹配和配准等等。

数学形态学的应用不仅仅局限在图像领域，它还可以应用于信号处理、文本分析、医学影像等其他领域。

以图像分割为例，数学形态学可以通过结构元素的逐步腐蚀或膨胀操作来准确地提取目标的轮廓。

首先，选择合适的结构元素，使其大小和形状适应目标的尺寸和形态特征。

然后，通过不断的腐蚀操作，可以逐渐消除目标周围的无关细节，最终得到目标的边界。

类似地，通过不断的膨胀操作，可以填补和连接目标内部的空洞，并得到目标的内部结构。

通过这种方式，数学形态学可以实现对复杂图像的准确分割，为图像识别和分析提供了可靠的基础。

总之，数学形态学是一种重要的数学方法和理论，它在图像处理、模式识别和计算机视觉等领域中具有广泛的应用和深远的意义。

实验六数学形态学及其应用

实验六数学形态学及其应用

实验六： 数学形态学及其应用实验原理腐蚀和膨胀是数学形态学最基本的变换，数学形态学的应用几乎覆盖了图像处理的所有领域，给出利用数学形态学对二值图像处理的一些运算。

膨胀就是把连接成分的边界扩大一层的处理。

而收缩则是把连接成分的边界点去掉从而缩小一层的处理。

二值形态学II (xx ,yy ), TT (ii ,jj )为0011⁄图像 腐蚀：EE (xx ,yy )=(II ⊙TT )(xx ,yy )=�[II (xx +ii ,yy +jj )&TT (ii ,jj )]mm ii ,jj=00膨胀：DD (xx ,yy )=(II ⊕TT )(xx ,yy )=�[II (xx +ii ,yy +jj )&TT (ii ,jj )]mm ii ,jj=00灰度形态学TT (ii ,jj )可取0011⁄以外的值 腐蚀： EE (xx ,yy )=(II ⊙TT )(xx ,yy )=mmii mm 00≤ii ,jj≤mm−11[II (xx +ii ,yy +jj )−TT (ii ,jj )] 膨胀： DD (xx ,yy )=(II ⊕TT )(xx ,yy )=mmmmxx 00≤ii ,jj≤mm−11[II (xx +ii ,yy +jj )+TT (ii ,jj )]1.腐蚀Erosion ： XX ⊙BB ={xx :BB xx ⊂xx }B 1删两边B 2删右上2.膨胀Dilation ： XX ⊕BB ={xx :BB xx ↑xx }B1补两边B2补左下3.开运算open：XX BB=(XX⊙BB)⊕BB4.闭运算close：XX BB=(XX⊕BB)⊙BB代码1：function[]= fs()I=imread('finger.tif');subplot(1,2,1),imshow(I);title('原图');BW=I;BW=rgb2gray(BW);SE=strel('square',2);%结构元素为边长2像素的正方形BW=imopen(BW,SE);%开运算（先腐蚀再膨胀）可以消除小物体、在纤细点处分离物体、平滑较大物体的边界。

第8章_数学形态学及其应用

第8章_数学形态学及其应用


第八章 数学形态学及其应用
b a A (a) (b) B A
元素与集合间的关系
第八章 数学形态学及其应用
2. 交集、 并集和补集 两个图像集合 A 和 B 的公共点组成的集合称为两个集合的交 集， 记为 A∩B ，即 A∩B={a ｜ a∈A 且 a∈B} 。两个集合 A 和 B 的 所 有 元 素 组 成 的 集 合 称 为 两 个 集 合 的 并 集 ， 记 为 A∪B ， 即
信息的“探针”， 称为“结构元素”。“结构元素”一般用大
写英文字母表示，例如用S表示。在图像中不断移动结构元素， 就可以考察图像之间各部分的关系。一般，结构元素的尺寸要 明显小于目标图像的尺寸。
第八章 数学形态学及其应用
8.2
二值形态学
二值形态学中的运算对象是集合。设A为图像集合，
S 为结构元素，数学形态学运算是用 S 对 A 进行操作。
第八章 数学形态学及其应用
(a)
(b)
(c)
开、
(a) 原始图像； (b) 开运算的结果； (c) 闭运算的结果
第八章 数学形态学及其应用
8.2.4 击中／击不中(Hit/Miss)变换
1.定义
设X是被研究的图像， S是结构元素，而且S由两个 不相交的部分S1和S2组成，即S=S1∪S2，且S1∩S2= 于是，X被S“击中”（X⊙S）的结果定义为
论层面上第一次引入了形态学的表达式，建立了颗粒分析方法。
第八章 数学形态学及其应用 2. 基本思想 数学形态学方法利用一个称作结构元素的“探针”收集图 像的信息，当探针在图像中不断移动时， 便可考察图像各个部 分之间的相互关系，从而了解图像的结构特征。数学形态学基 于探测的思想，与人的FOA(Focus Of Attention)的视觉特点有 类似之处。作为探针的结构元素，可直接携带知识（形态、大
胡学龙《数字图像处理(第二版)》课后习题解答

胡学龙《数字图像处理(第二版)》课后习题解答


2
1．PHOTOSHOP：当今世界上一流的图像设计与制作工具，其优越性能令其产品望尘 莫及。PHOTOSHOP 已成为出版界中图像处理的专业标准。高版本的 P扫描仪、数码相机等图像输入设备采集的图 像。PHOTOSHOP 支持多图层的工作方式，只是 PHOTOSHOP 的最大特色。使用图层功能 可以很方便地编辑和修改图像，使平面设计充满创意。利用 PHOTOSHOP 还可以方便地对 图像进行各种平面处理、绘制简单的几何图形、对文字进行艺术加工、进行图像格式和颜色 模式的转换、改变图像的尺寸和分辨率、制作网页图像等。
1.5 常见的数字图像处理开发工具有哪些？各有什么特点？ 答．目前图像处理系统开发的主流工具为 Visual C++（面向对象可视化集成工具）和 MATLAB 的图像处理工具箱（Image Processing Tool box）。两种开发工具各有所长且有相互 间的软件接口。 Microsoft 公司的 VC++是一种具有高度综合性能的面向对象可视化集成工具，用它开发 出来的 Win 32 程序有着运行速度快、可移植能力强等优点。VC++所提供的 Microsoft 基础 类库 MFC 对大部分与用户设计有关的 Win 32 应用程序接口 API 进行了封装，提高了代码 的可重用性，大大缩短了应用程序开发周期，降低了开发成本。由于图像格式多且复杂，为 了减轻程序员将主要精力放在特定问题的图像处理算法上，VC++ 6.0 提供的动态链接库 ImageLoad.dll 支持 BMP、JPG、TIF 等常用 6 种格式的读写功能。 MATLAB 的图像处理工具箱 MATLAB 是由 MathWorks 公司推出的用于数值计算的有 力工具，是一种第四代计算机语言，它具有相当强大的矩阵运算和操作功能，力求使人们摆 脱繁杂的程序代码。MATLAB 图像处理工具箱提供了丰富的图像处理函数，灵活运用这些 函数可以完成大部分图像处理工作，从而大大节省编写低层算法代码的时间，避免程序设计 中的重复劳动。MATLAB 图像处理工具箱涵盖了在工程实践中经常遇到的图像处理手段和 算法，如图形句柄、图像的表示、图像变换、二维滤波器、图像增强、四叉树分解域边缘检 测、二值图像处理、小波分析、分形几何、图形用户界面等。但是，MATLAB 也存在不足 之处限制了其在图像处理软件中实际应用。首先，强大的功能只能在安装有 MATLAB 系统 的机器上使用图像处理工具箱中的函数或自编的 m 文件来实现。其次，MATLAB 使用行解 释方式执行代码，执行速度很慢。第三，MATLAB 擅长矩阵运算，但对于循环处理和图形 界面的处理不及 C++等语言。为此，通应用程序接口 API 和编译器与其他高级语言（如 C、 C++、Java 等）混合编程将会发挥各种程序设计语言之长协同完成图像处理任务。API 支持 MATLAB 与外部数据与程序的交互。编译器产生独立于 MATLAB 环境的程序，从而使其他 语言的应用程序使用 MATLAB。
第八章(1)-数字形态学及其应用

第八章(1)-数字形态学及其应用


b
A
a
a∈ A b∉ A
结构元素(Structure Element) 设有两幅图像A和B，若A是被处理的对象，B 是用来处理A的，则称B为结构元素。
7
第八章 数字形态学及其应用
交集、 并集和补集
AI B
AU B
AC
A B A
B A
B
A I B = {a a ∈ A且 a ∈ B}
A U B = {a a ∈ A或 a ∈ B} AC = {a a ∉ A}
2
第八章 数字形态学及其应用
利用数学形态学进行图像分析的基本步骤如下： 1、提出所要描述的物体几何结构模式，即提取物 体的几何结构持征； 2、根据该模式选择相应的结构元素，结构元素应该 2 简单而对模式具有最强的表现力； 3、用选定的结构元对图像进行击中与否(HMT)变 换，便可得到比原始图像显著突出物体特征信息的 图像。如果赋予相应的变量．则可得到该结构模式 的定量描述； 4、经过形态变换后的图像突出需要的信息，此时 就可以方便地提取信息。
8
第八章 数字形态学及其应用
差集
A − B = {x x ∈ A, x ∉ B} = A I B c
A B
9
第八章 数字形态学及其应用
平移转换：设A是两个二维集合，A中的元素是 定义 x = ( x1 , x2 )
a = (a1 , a2 )
则： ( A) x = c c = a + x, for a ∈ A
4 3 2 1 0 1 2 3 4 5 6
b∈B
0 1 2 3 4 5 6
(a) 图像X与结构元素B 4 3 2 1 0 1 2 3 4 5 6 (c)
(b) ( X 膨胀的等价定义形式： X ⊕ B = U ( X)b2b ) 4 3 2 1
数学形态学原理

数学形态学原理

大为S+x，这就是膨胀运算，记为X S。若用集合语言，
它的定义为
X S = {x| S+x∪x≠ }
图中X是被处理的对象，B是结构元素，对于任意一个在 阴影部分的点a，Ba击中X，所以X被B膨胀的结果就是那个阴 影部分。阴影部分包括X的所有范围，就象X膨胀了一圈似的， 这就是为什么叫膨胀的原因。
6.2.6 由于开、闭运算是在腐蚀和膨胀运算的基础上定义的， 根据 腐蚀和膨胀运算的代数性质，我们不难得到下面的性质。
1） 对偶性 (XC○S)C = X●S ， (XC●S)C = X○S
2）扩展性（收缩性） X○S X X●S
即开运算恒使原图像缩小，而闭运算恒使原图像扩大
3） 单调性 如果X Y，
数学形态学的数学基础和所用语言是集合论，因此它 具有完备的数学基础，这为形态学用于图像分析和处理、形 态滤波器的特性分析和系统设计奠定了坚实的基础。
数学形态学的应用可以简化图像数据，保持它们基本 的形状特性，并除去不相干的结构。
数学形态学方法利用一个称作结构元素的“探针”收集 图像的信息，当探针在图像中不断移动时， 便可考察图像各 个部分之间的相互关系，从而了解图像的结构特征。
X S {x|Sx X }
X用S腐蚀的结果是所有使S平移x后仍在X中的x的集合。
换句话说，用S来腐蚀X得到的集合是S完全包括在X中时S的
原点位置的集合。
对于任意一个在阴影部分的点a，Ba 包含于X，所以X被B 腐蚀的结果就是那个阴影部分。阴影部分在X的范围之内，且 比X小，就象X被剥掉了一层似的，这就是为什么叫腐蚀的原因
二值 图像
腐蚀
膨胀
图 腐蚀与膨胀示意图
6.2.4 １．开运算
先腐蚀后膨胀称为开 对图像X及结构元素S，用符号X○S表示S对图像X作开运算
数学形态学及应用

数学形态学及应用

y 5
4 3 2 1 0 1 2 3 4 x y 3 2 1 0 b 1 2 3 4 x 5 4 3 2 1 0 1 2 3 4 x
y
(a )数字图像
(b )点
(c)
A被b平移：A＋b＝{a＋b| a∈A} ————a与b对应坐标相加
5 4 3 2 1 0
y
x 4 3 2 1 0 1 2 3 4 y
C ⊙ X S {x | S1 x X且S2 x X }
C ⊙ X S ( XS1 ) ( X S2 )
( XS1 ) ( X S ) ( XS1 ) ( X S )
V 2
V C 2
X被S击中的结果相当于X被S1腐蚀的结果与X 被S2的反射集S2V膨胀的结果之差。
区域填充
骨架提取
骨架提取是由细化而来。骨架形成的是单像素的细化结果
粗化
连通分量提取
(a)X光图 像
(b)二值图 像 (c)用5×5 结构元 素腐蚀 结果
灰度级图像扩展
（a）原图 （b）膨胀图，更亮了减弱了暗细节 （c）腐蚀图，更暗了，明亮成分减 少
注意不同图中亮和暗细节的变化
一、膨胀 使图像扩大
A和B是两个集合，A被B膨胀定义为：
上式表示：B的反射进行平移与A的交集不为空 B的反射：相对于自身原点的映象 B的平移：对B的反射进行位移
膨胀的另一个定义
上式表示：B的反射进行平移与A的交集是A的子集
膨胀操作过程
将结构元素B的原点移至集合A的某一点,
将结构元素B中点的坐标与集合A中该点坐标相加, 得到对集合A中一点膨胀的运算结果.
击中/击不中变换的应用
• 严格的模版匹配。指出被匹配点所应满足的 性质（模板形状）的同时也指出这些点所不 应满足的性质，即对周围环境背景的要求。 • 保持拓扑结构的形状细化，以及形状识别和
数学形态学发展及应用

数学形态学发展及应用

摘要摘要数学形态学兴起于20世纪60年代，是一种新型的非线性算子，它着重研究图像的几何结构，由于视觉信息理解都是基于对象几何特性的，因此它更适合视觉信息的处理和分析，这类相互作用由两种基本运算腐蚀和膨胀及它们的组合运算来完成。

为了跟踪国际前沿，发展我国的非线性信号处理技术，进一步研究形态学理论和应用技术及非常必要而有实际意义的。

本文首先深入地讨论了数学形态学的基本理论，详细介绍了数学形态学的起源、发展；从二值形态学推广到灰度形态学，并分析和介绍了数学形态学在图像处理中的具体应用,并对数学形态学的现状和未来发展方向进行总结。

具体论述步骤分为以下几个方面：1>学习和总结了数学形态学的基本理论。

2>研究了二值形态学、灰度形态学、彩色形态学的算法理论。

3>列举并总结数学形态学在图像分割、边缘检测及图像滤波等方面的应用。

4>对两种图像的边缘检测进行简单的MATLAB实现。

5>对数学形态学的现状及发展方向进行总结和展望。

关键词：数学形态学二值图像灰度图像彩色形态学边缘检测图像分割形态滤波ABSTRACTABSTRACTMathematics morphology rose in the sixties of the 20th century, it was a kind of new-type non-linear operator.It studies the geometry structure of the image,because vision information is comprehended based on geometry characteristics of the target,so it is suitable for the information processing and analyse of the vision.This kind of interaction is accomplished by two kinds of basic operation; erosion and dilation. In order to follow the international front and develop the non-linear signal processing technology of our country, study the morphology theory and application technology are very necessary and have actual meaning further.Above all in this paper the basic theory of mathematical morphology is discussed,then we introduce origin of mathematics morphology from binary morphology to gray morphology and extensively study lts diffent operators and quality. Its application in image processing is analysed and introduced as well. Then it tally up the present condition and develop direction of the mathematics morphology. Concrete discuss a step to is divided into a few aspects as follows：1>Study and summary the basic theories of mathematics morphology.2>Investigate the theories of binary morphology. grayscale morphology and color morphology.3>Enumerate and tally up the applied in image segmentation. edge detection and morphological filter.4>Carry out the edge detection of two kinds of image with matlab.5>Summary and outlook the present condition and developing direction of mathematics morphology.Keywords：Mathematics morphology. Binary image. Grayscale inage. Color morphology. Edge detection. Image segmentation. Morphological filter.目录i目录第一章绪论 (1)1.1 引言 (1)1.2 数学形态学发展简史 (1)第二章数学形态学基本理论 (5)2.1 引言 (5)2.2 二值形态学 (5)2.2.1 二值腐蚀 (5)2.2.2 二值膨胀 (6)2.2.3 二值开运算 (7)2.2.4 二值闭运算 (8)2.3 灰值形态学 (9)2.3.1 灰值腐蚀 (9)2.3.2 灰值膨胀 (10)2.3.3 灰值开运算 (11)2.3.4 灰值闭运算 (12)2.3.5 灰值形态学梯度 (14)2.4 彩色形态学 (15)2.4.1 彩色形态学简介 (15)2.4.2 分量法 (16)2.4.3 HLS法 (16)2.4.5 彩色形态学总结 (18)2.5 本章小结 (18)第三章数学形态学的应用 (20)3.1 引言 (20)3.1.1 数学形态学在图像处理中的主要应用 (20)3.1.2 图像边缘检测 (20)ii 数学形态学的发展及应用研究3.1.3 图像分割 (21)3.1.4 噪声滤除 (22)3.2 数学形态学应用于图像边缘检测 (22)3.2.1 图像边缘定义 (22)3.2.2 基本的形态学边缘检测算子 (22)3.2.3 抗噪型形态学边缘检测因子 (23)3.2.4 基于多结构元的图像边缘检测 (24)3.2.5 基于多尺度的形态学边缘检测 (27)3.3数学形态学应用于图像分割 (28)3.3.1 图像分割定义 (28)3.3.2 并行边界分割技术 (30)3.3.3 串行边界分割技术 (30)3.3.4 并行区域分割技术 (31)3.3.5 串行区域分割技术 (32)3.4 基于分水岭变换的彩色细胞图像分割 (33)3.4.1 k-均值聚类和分水岭变换 (33)3.4.2 分割方法统筹 (33)3.4.3 图解细胞均值聚类 (34)3.4.4 图解细胞分割过程 (36)3.4.5 结果与讨论 (38)3.5 数学形态学应用于图像噪声滤波 (38)3.5.1 滤波基本原理 (38)3.5.2 对噪声污染的颗粒图像滤波 (39)3.5.3 对差、并噪声同存图象的滤波 (40)3.5.4 总结 (42)3.6 本章小结 (42)第四章两种图像边缘检测的MATLAB仿真实现 (44)4.1结构元素的选择 (44)4.2 算法实现 (45)4.3 MATLAB仿真实验 (46)目录iii4.4 图像的滤波及边缘检测的MATLAB实现 (48)第五章总结与展望 (56)5.1数学形态学学习总结 (56)5.2 数学形态学发展过程中存在的问题 (57)5.3 数学形态学发展方向 (57)致谢 (58)参考文献 (60)iv 数学形态学的发展及应用研究第一章绪论 1第一章绪论1.1 引言1965年法国巴黎地质学家G.Matheron和J.Serra创立数学形态学理论,这是一门新兴的图象分析科学。

数学形态学及其应用

数学形态学及其应用


三、 灰度数学形态学
（一） 灰度图像的排序
对灰度图像讨论数学形态学的方法时不仅
要考虑空间位置还要考虑灰度的大小。
一个信号f (x)的定义域为
D[ f ] x : f ( x )
如果对所有的 x 都有g(x) ≤ f (x)，就说 g(x)
在f (x)的下方，并记为g(x) ≤ f (x)
（一）灰度图像的排序
• 二值信号：交集和并集操作
•
•
灰度信号：最小和最大操作
两个信号 f (x)和g(x)的最小值( f g)(x)
( f g )( x ) min f ( x ), g ( x )
如果 x D[f ] ∩ D[g]，那么( f g)(x)是 f (x)和g(x) 的最小值，否则( f g)(x) = –
b ( A) A ( A B)
(a)
(b)
(c)
(d)
结构元素是8-连通的，而所得到的边界是4-连通的
（三）二值形态学实用算法
3. 区域填充 X k X k 1 B Ac
k 1, 2, 3,
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
结构元素是4-连通的，而原填充的边界是8-连通的
腐蚀运算：A B A，或 A B A
膨胀和腐蚀
原点不包含在结构元素中时的膨胀运算 AAB
?
(a)
A在膨胀中自身完全消失了
(b)
(c)
(d)
? ? ?
(a)
(b)
(c)
(d)
膨胀和腐蚀
原点不包含在结构元素中时的腐蚀运算 A B A
图像分割

图像分割

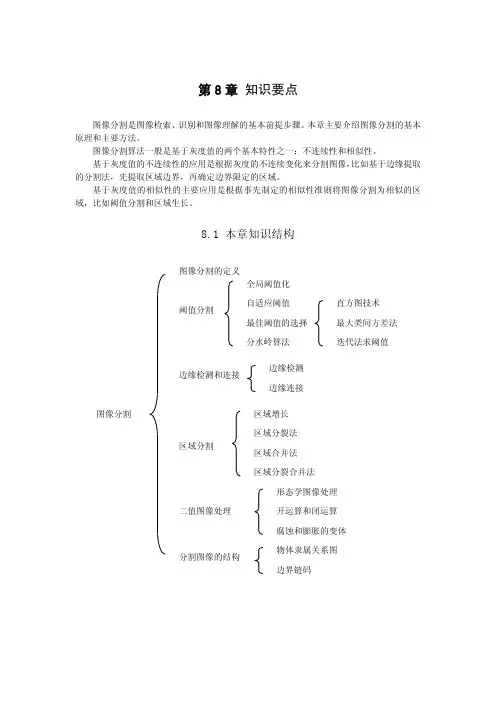
第8章 知识要点图像分割是图像检索、识别和图像理解的基本前提步骤。

本章主要介绍图像分割的基本原理和主要方法。

图像分割算法一般是基于灰度值的两个基本特性之一：不连续性和相似性。

基于灰度值的不连续性的应用是根据灰度的不连续变化来分割图像，比如基于边缘提取的分割法，先提取区域边界，再确定边界限定的区域。

基于灰度值的相似性的主要应用是根据事先制定的相似性准则将图像分割为相似的区域，比如阈值分割和区域生长。

8.1 本章知识结构8.2 知识要点1. 图像分割在对图像的研究和应用中，人们往往仅对图像中的某些部分感兴趣。

这些部分常称为目标或前景（其它部分称为背景），它们一般对应图像中特定的、具有独特性质的区域。

为了检索、辨识和分析目标，需要将它们分离提取出来，在此基础上才有可能对目标进一步利用。

图像分割就是指把图像分成各具特性的区域并提取出感兴趣目标的技术和过程。

图像分割是由图像处理过渡到图像分析的关键步骤。

一方面，它是目标表达的基础，对特征测量有重要的影响；另一方面，因为图像分割及其基于分割的目标表达、特征提取和参数测量等，能将原始图像转化为更抽象更紧凑的形式，所以使得更高层的图像分析和理解成为可能。

图像分割的应用非常广泛，几乎出现在有关图像处理的所有领域中，并涉及各种类型的图像。

图像分割在基于内容的图像检索和压缩、工业自动化、在线产品检验、遥感图像、医学图像、保安监视、军事、体育、农业工程等方面都有广泛的应用。

例如：在基于内容的图像检索和面向对象的图像压缩中，将图像分割成不同的对象区域等；在遥感图像中，合成孔径雷达图像中目标的分割，遥感云图中不同云系和背景分布的分割等；在医学应用中，脑部图像分割成灰质、白质、脑脊髓等脑组织和其它脑组织区域等；在交通图像分析中，把车辆目标从背景中分割出来等。

在各种图像应用中，只要需要对图像目标进行提取、测量等，就都离不开图像分割。

图像分割的准确性将直接影响后续任务的有效性，因此图像分割具有十分重要的意义。

数学形态学及其在图像分析中的应用

第35卷，增刊红外与激光工程2006年10月Im删姐d kcr En西nee曲g oc t．2006 V01．35Suppl e眦m数学形态学及其在图像分析中的应用陈爱军(东北林业大学机电工程学院，黑龙江哈尔滨150040)摘要：数学形态学作为一门新兴的、以形态为基础对图像进行分析的学科，已得到人们的广泛关注，并应用于图像处理的许多方面，如噪声抑制、特征提取、边缘检测、图像分割、形状识别、纹理分析、图像恢复与重建等。

首先介绍了几种基本的数学形态学算子及其特点，然后介绍了星体分布统计和粒子分析两个运用数学形态学进行图像分析的具体例子，给出了具体实现步骤，并通过编程得到了实验结果。

最后对全文进行了总结。

关键词：数学形态学；图像分析；高帽变换；低帽变换；粒子分析中圈分类号：T P391文l畎标识码：A文章编号：1007—2276(2006)增D．0465．04M at hem at i cal m or phol ogy锄d i t s appl i c at i on i n i m age锄al ys i s、C胍N础-j吼(C oⅡ端c of M∞hi nt：fy彻d El∞缸锄i c勘嚼∞cri ng，N or m e私t F伽e s缸y U ni vc珏自啊II{Ⅲn150040。

a血a)A bst r a ct：M am em a t i ca l m o印hol ogy i s a r i si ng蚰bj ect，w l l ich has舭t ed m or e加d m or e a ne nt i on．It h船be en apphe d i n m any a spec t s of i m a ge proce s si Il g，such as noi s e r esm l i Il i ng，fea t ure e xt r ac t i on，e dge de t e ct i on，i I I l age se gI Il ent a t i on，shape r e cogI l i t i on，t ext ur e al l al ysi s，i111age re st O r at i on and r e st nl c t i on．Fi r sⅡy，s eV e r a l baL s i c oper at o r s of m a m e m a t i c al m o平hol ogy ar e pr es ent ed．T hen，t、Ⅳo ex锄pl es of s t ar di s t ri but i ng aI l al ys i s锄d pani cl e aI l al ys i s a r e i n廿l m uced t o s how how t o pr oces s i m ages us i ng m a t hem撕ca l m or ph0109y．T he i m pl e m e nt pr oces s i s des cri bed i nd砌1aJl d t tl e s i m ul at i onexper i m ent s a r e obt ai ned by pm磬韧疵ng．w or ds：M at hem at i cal m oI phol ogy：hI强ge锄al ysi s；Top—hat仃ansf om；B0t-hat咖s fo皿；K eyP a r t i cl c aI l al ys i sO引育数学形态学(m a t hem at i c al m o叩hol ogy)诞生于1964年，最初它只是分析几何形状和结构的数学方法，是建立在数学基础上用集合论方法定量描述几何结构的科学。

数学形态学在图像处理中的应用


灰度形态学运算
灰度腐蚀
灰度膨胀
通过结构元素来腐蚀灰度图像，使图像的亮 度值发生变化，达到去噪声、平滑图像的目 的。
通过结构元素来膨胀灰度图像，扩大亮区范 围，连接断开的物体。
灰度开运算
灰度闭运算
先进行灰度腐蚀操作，再进行灰度膨胀操作 ，可以消除小的物体，同时平滑边界。
先进行灰度膨胀操作，再进行灰度腐蚀操作 ，可以填充小的孔洞，同时平滑边界。
彩色形态学运算
彩色腐蚀
通过结构元素来腐蚀彩色图像，使 图像的颜色发生变化，达到去噪声 、平滑图像的目的。
彩色膨胀
通过结构元素来膨胀彩色图像，扩 大颜色范围，连接断开的物体。
彩色开运算
先进行彩色腐蚀操作，再进行彩色 膨胀操作，可以消除小的物体，同 时平滑边界。
彩色闭运算
先进行彩色膨胀操作，再进行彩色 腐蚀操作，可以填充小的孔洞，同 时平滑边界。
可能改变图像特征
如果使用不当，数学形态学方法 可能会改变图像中的一些特征， 这可能会对后续处理产生影响。
对噪声敏感
如果图像中存在噪声，数学形态 学方法可能会将噪声放大，导致 处理效果不佳。
05
数学形态学在图像处理中的未来展望及改
进建议
未来展望
理论深入研究
数学形态学作为一门新兴的交叉学科，其理论体 系仍需进一步深化和完善。未来，可以期待在理 论创新方面取得更多突破。
• 图像分割：通过形态学运算将图像分割成不同的 区域或对象，方便后续的分析和处理。
• 特征提取：利用形态学运算提取图像中的 形状和结构信息，用于识别和分类。
• 图像压缩：通过形态学运算实现图像的压缩 和编码，降低存储空间的需求。
• 图像恢复：利用形态学运算来修复和恢复 图像中的缺失或损坏部分，实现图像的修 复和还原。

第8章_数学形态学_中文.


111
第8章 数学形态学 Morphological Image Processing
模板卷积和中值滤波思考
思考问题： (1) 模板形状能否变化，是否一定是正方形模板 (2) 模板所覆盖的像素除了做积分、微分和取灰度中值之外，能否进 行其他运算? 要解决这两个问题，就需要用到本章的数学形态学。 在数学形态学中，模板称为结构元素或探针，模板所取出的像素按 灰度排序，取最大值或最小值，分别称为膨胀和腐蚀。
第8章 数学形态学 Morphological Image Processing
模板卷积回顾2
第8章 数学形态学 Morphological Image Processing
中值滤波回顾
2. 二维中值滤波：
与均值滤波类似，做3*3的模板，对9个数排序，取第5 个数替代原来的像素值。
111
191
1
8.1 引言
2. 基本符号和术语 (5) 目标和结构元素 目标图像：待处理的图像 目标：通常指图像中像素值不为0的点 结构元素：考察目标图像各部分之间的关系时，需要设计一种收 集信息的“探针”，称为结构元素。
A
B
第8章 数学形态学 Morphological Image Processing
第8章 数学形态学 Morphological Image Processing
模板卷积回顾1
如用3×3的模板：
1 1 1
1 9
1 1
1 1
1 1
12143 12234 57689 57688 56789
12143 1 23 24 34 4 5 74 56 86 9 5 76 76 8 8 56789
8.2 二值形态学
2. 腐蚀演示
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
5 4 3 2 1 0
y y
3 2 1 0 5 4 3 2 1 1 2 3 (b) 4
y
平移
1 2 3 (c) 4
b
x
0
1
2 3 (a)
4
x
x
15
第八章 数学形态学及其应用
反射： A关于图像原点的反射定义为： Av={a| -a ∈ A} 即将A中的每个点的坐标取反后所得到的新图像 （关于原点对称） 。
SE = strel('disk disk',R,N) creates a flat, disk-shaped structuring element, where R specifies the radius.
21
第八章 数学形态学及其应用
SE = strel('line 'line',LEN,DEG) creates a flat, linear structuring element, where LEN specifies the length, and DEG specifies the angle (in degrees) of the line, as measured in a counterclockwise direction from the horizontal axis.
6
第八章 数学形态学及其应用
数学形态学是由一组形态学的代数运算子组成的，它 的基本运算有4个：
腐蚀（或侵蚀）- Erosion 膨胀（或扩张）- Dilation 开启 - Opening 闭合 - Closing
基于这些基本运算还可推导和组合成各种数学形 态学实用算法，用它们可以进行图像形状和结构的分 析及处理，包括图像分割、特征抽取、边界检测、图 像滤波、图像增强和恢复等。
y x
5 4 3 2 2 1 3 4 1 4 3 2 1 0
y
0 1 2 (c) 3 4
x
(d)
反射
16
第八章 数学形态学及其应用
平移和反射
ˆ B = {w w = −b, b ∈ B}
反射
集合原点
平移
(B)z={c｜c=a+z , a∈B}
17
第八章 数学形态学及其应用
5. 目标和结构元素
目标图像：被处理的图像称为目标图像 目标图像： 目标图像，一般用大写英文 字母表示。为了确定目标图像的结构，必须逐个考察图像 各部分之间的关系，并且进行检验，最后得到一个各部分 之间关系的集合。 结构元素：在考察目标图像各部分之间的关系时，需要设 结构元素： 结构元素”。“结 计一种收集信息的“探针”， 称为“结构元素 构元素”一般用大写英文字母表示，例如用S表示。在图 像中不断移动结构元素，就可以考察图像之间各部分的关 系。一般，结构元素的尺寸要明显小于目标图像的尺寸。
二二二二 腐腐 膨膨
23
第八章 数学形态学及其应用
8.2.1 腐蚀(Erosion)
给定目标图像 X 和一个结构元素 S， S 对X的腐蚀 (简称腐蚀，有时也称 X 用 S 腐蚀， X 被 S 腐蚀)的定义 为： X ㊀ S={ x | S + x ⊆ X } 上式表明，X 用 S 腐蚀的结果是所有使 S 平移到 x 后，S 仍在 X 中的x 的集合。 S 换句话说，用 S 来腐蚀 X 得到的集合是 S 完全包括 在 X 中时 S 的原点位置的集合 的原点位置的集合。
4
第八章 数学形态学及其应用
数学形态学的基本思想是用具有一定形态的结构元素去 数学形态学的基本思想 量度和提取图像中的对应形状以达到对图像分析和识别 的目的。 数学形态学利用结构元素作为“探针”，收集图像的信 息；当探针在图像中不断移动时，便可考察图像各个部 分之间的相互关系，从而了解图像的结构特征 结构特征。 作为探针的结构元素，可直接携带知识（形态、大小、 甚至加入灰度和色度信息）来探测、研究图像的结构特 点。数学形态学基于探测的思想，与人的FOA (Focus Of Attention)的视觉特点有类似之处。
14
第八章 数学形态学及其应用
4.平移和反射
平移： 设A是一幅数字图像，b是一个点，那么定义A被 b平移后的结果为： A＋b＝{a＋b| a∈A} ＋ ＝ ＋ ∈ 即取出 A 中的每个点a的坐标值，将其与点b的坐标 值相加，得到一个新的点的坐标值a+b，所有这些新点 所构成的图像就是A被b平移的结果，记为A+b。
SE = strel('rectangle rectangle',MN) creates a flat, rectangle-shaped structuring element, where MN specifies the size.
22
第八章 数学形态学及其应用
8.2 二值形态学
设 A 为图像集合，S 为结构元素，数学形态学运算是 用 S 对 A 进行操作。 腐蚀与膨胀是二值形态学中两个最基本的运算。在腐 蚀和膨胀两个基本运算的基础上，可以构造出由膨胀和腐 蚀两个运算的复合与集合操作（并、交、补等）组合而成 的形态学运算族，如 开启、闭合、击中/击不中变换等。
9
第八章 数学形态学及其应用
数学形态学中的集合：表示图像中的不同目标(Objects)。
例如，在二值图像中，常用取值为1的点代表前景，而取值为0 例如，在二值图像中，常用取值为1的点代表前景，而取值为0的点 代表背景。所有取值为1的像素的集合是图像完整的形态学描述。 代表背景。所有取值为1的像素的集合是图像完整的形态学描述。
㊀
S）将是 X
的一个收缩，即X㊀S ⊆X（当O∈S时）；如果 S 不包含
28
第八章 数学形态学及其应用
腐蚀的另一种定义形式:
利用腐蚀运算的定义式可以直接设计腐蚀变换的算法。 但有时为了更方便，常使用腐蚀的另一种表达式，即 X ㊀ S = ∩{s + X | -s ∈ S} 上式把腐蚀表示为对图像X平移的交 对图像 平移的交，这在某些并行 处理环境中特别有用。（注意：对结构元素进行了反射操 （注意： 作）
12
第八章 数学形态学及其应用
13
第八章 数学形态学及其应用
3.击中（Hit）与击不中（Miss）
设有两幅图像A和B，如果A∩B≠∅，那么称B击中A，记 为A⊙B（或 A↑B ）； 否则，如果A∩B= ∅ ， 那么称B击不中A。
A
B
A
B
(a)
(b)
图8-3 击中与击不中 （a） B击中A； （b） B击不中A
8
第八章 数学形态学及其应用
8.1.2 基本符号和术语
1. 元素和集合 在形态学运算中，把一幅图像称为一个集合。对于二值 图像而言： 取值为1的点（像素）对应于景物， 取值为0的点（像素）对应于背景。 考虑所有值为1的点的集合为 A， 则 A 与图像是一一对 应的。 对于一幅图像 A，如果点 a 在 A 的区域以内， 那么就说 a 是 A 的元素，记为 a∈A，否则，记作a∉A。 ∉
5
第八章 数学形态学及其应用
数学形态学的数学基础和所用语言是集合论。
因此它具有完备的数学基础，这为形态学用于图像分析和处理、 因此它具有完备的数学基础，这为形态学用于图像分析和处理、 形态滤波器的特性分析和系统设计奠定了坚实的基础。 形态滤波器的特性分析和系统设计奠定了坚实的基础。
数学形态学的应用可以简化图像数据，保持它们基本的 保持它们基本的 形状特性，并除去不相干的结构。 形状特性，并除去不相干的结构 数学形态学的算法具有天然的并行实现的结构， 实现 了形态学分析和处理算法的并行，大大提高了图像分析 和处理的速度。
0 y
x
二维整数空间(Z2) 注意：硬件显示时将取值为“1”的像素显示为“白色”、“0”显示为 “黑色”，而印刷时常相反。 “1”为白色或黑色，取决于事先的约定。
10
第八章 数学形态学及其应用
包含: 包含: 对于两幅图象 A 和 B，如果对B中的每一个点 b (b ∈B） 都有 b ∈A，那么称 B 包含于 A，记作 B⊆A。如果同时A 中存在一个点 a，a ∈A 且 a ∉B，那么称 B 真包含于A，记 作B⊂A。
24
第八章 数学形态学及其应用
S+x只有三种可能的状态:
(1) S+x ⊆ X； (2) S+x ⊆ XC； (3) S+x∩X 与 S+x∩X C 均不为空
图8-6 S+x的三种可能的状态
25
第八章 数学形态学及其应用
例8-1 腐蚀运算图解。图8-7给出腐蚀运算的一个简 单示例。由图可见，腐蚀将图像（区域）收缩小了。
b a A (a) a ∈A 且 a ∉B (b) B ⊂ A B A
图8-1 元素与集合间的关系
11
第八章 数学形态学及其应用
2. 交集、并集、补集和差集
交集：两个图像集合 A 和 B 的公共点组成的集合称为 两个集合的交集， 记为A∩B，即 A∩B={a｜a∈A且a∈B} 并集：两个集合 A 和 B 的所有元素组成的集合称为两 个集合的并集，记为A∪B，即 A∪B={a｜a∈A，或a∈B} 补集：对一幅图像A，在图像 A 区域以外的所有点构成 的集合称为A的补集，记为AC，即AC={a｜a ∉ A}。 差集：A-B={a|a∈A且a ∉B}=A ∩Bc
20
第八章 数学形态学及其应用
Matlab 的结构元素函数
SE = strel(shape, parameters) SE = strel('diamond diamond',R) creates a flat, diamond-shaped structuring element, where R specifies the distance from the structuring element origin to the points of the diamond.