第1页(共4页)

《自动控制原理1》试卷 第1 页 共4 页中国计量大学2019年硕士研究生招生考试试题考试科目代码：801 考试科目名称：自动控制原理1所有答案必须写在报考点提供的答题纸上，做在试卷或草稿纸上无效。

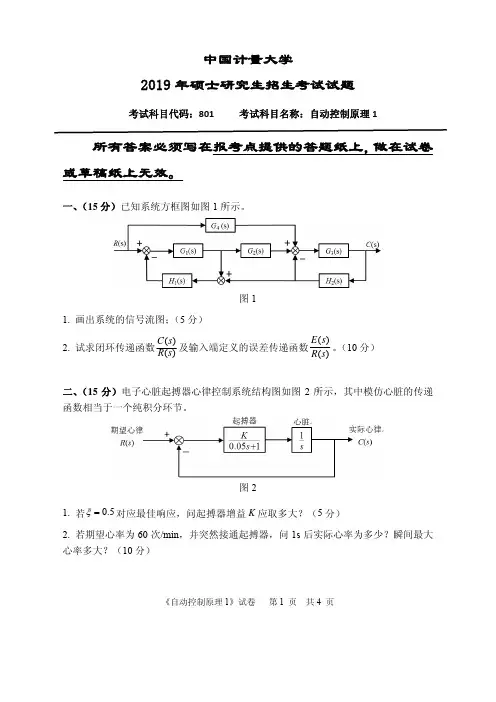
一、（15分）已知系统方框图如图1所示。

图11. 画出系统的信号流图；（5分）2. 试求闭环传递函数)()(s R s C 及输入端定义的误差传递函数)()(s R s E 。

（10分）二、（15分）电子心脏起搏器心律控制系统结构图如图2所示，其中模仿心脏的传递函数相当于一个纯积分环节。

图21. 若5.0=ξ对应最佳响应，问起搏器增益K 应取多大？（5分）2. 若期望心率为60次/min ，并突然接通起搏器，问1s 后实际心率为多少？瞬间最大心率多大？（10分）《自动控制原理1》试卷 第2 页 共4 页三、（15分）系统结构图如图3所示，[]()()()e t r t b t =−。

图31. 已知G 1(s )的单位阶跃响应为21e t −−，试求G 1(s )；（5分） 2. 利用求出的G 1(s )，当r (t )=10·1(t )时，试求：①系统的稳态输出；②系统的超调量、调节时间和稳态误差。

（10分）四、（15分）已知系统结构图如图4所示：图41. 绘出K *从0→+∞变化时系统的根轨迹；（8分）2. 确定系统处于欠阻尼条件下的K *范围；（4分）3. 确定系统稳定时的最小阻尼比。

（3分）五、（15分）已知系统传递函数为)52)(2()(2+++=s s s K s G ，1. 画出奈奎斯特图；（10分） 2. 当K =52，利用奈奎斯特稳定判据判断其闭环系统的稳定性。

（5分）六、（15分）已知最小相位开环系统的渐近对数幅频特性如图5所示，试求： 1. 系统的开环传递函数；（4分） 2. 截止频率c ω和相角裕量γ；（8分）3. 若使截止频率s rad c /10=ω，其放大倍数应取多少？（3分）《自动控制原理1》试卷 第3 页 共4 页七、（20分）已知采样系统结构如图6所示，其中采样周期s T 4.0=。

word设置页码“第⼏页共⼏页”的⽅法设置页码“第⼏页共⼏页”的⽅法要求：1、⾸页与第⼆页不需要页码（即放置⽬录，勿需页码），第三页插⼊页码，从第1页开始；2、不需要页眉；3、页码格式为“第⼏页共⼏页”，且“共⼏页”显⽰的是从第⼀页开始计数，⽽不是所有的页数。

解决⽅法：1、把光标放在⽂档的顶端；页⾯布局——分隔符——分节符（下⼀页）2、插⼊——页码——设置页码格式——起始页码从0开始（默认为1）；3、此时不是有页眉吗？双击（选中⾸页不同）；就出现了⼀个⼲⼲净净的空⽩页了，⽽且页码从第⼆页开始计数！但是我要的是两张空⽩页呀？简单，同理，⿏标放在空⽩页，如上操作即可做出⼀个相同的空⽩页；即使你要100张这样的空⽩页也能给你做出来。

如何插⼊页码：引⽤——⽬录——插⼊⽬录——确定即可（前提是你设置了各个等级的标题，否则不顶事！）虽然Word2007提供了许多页脚样式，我却没有发现这⼀格式。

于是就只能⼿动进⾏编辑了。

当然了，页数不能够⽤⼿⼯去输⼊，不然⽂档页⾯⼀多就得累死。

所以引⽤域就好了。

在域中{numpages}是表⽰总页数，{page}当前第⼏页数。

在页脚处输⼊共页/第页。

然后把光标移到共页之间，按Ctrl+F9，插⼊域，输⼊代码就好了，后⾯的⼀样操作。

插⼊域完了再按Alt+F9就运⾏（更新域）了，此时就可以看到刚才的域代码起作⽤了（word2003就直接选择就⼤⽬的）。

最后，当所有的⽂档编辑结束后，你可以在页脚处修改总页数为你实际的论⽂的页数，因为如果算上封⾯，保密协议，⽬录，多出⼗⼏页，别⼈⼀看，以为你在写⼩说呢！对于word2003这些就很简单了：1、插⼊——分隔符——下⼀页，这样就分节了2、插⼊——页码——⾼级——起始页码13、每节分布插⼊，不需要页码的就⾸页不显⽰页码在word2003下word⽂档在同⼀⽂件中插⼊页码时，总是从第⼀页到末页顺序编码，但我这⼀⽂件从第1—4页为“提纲”或者“前⾔”，不需编页码，从第5页开始才是正⽂，那么怎样才能使页码从第5页开始顺序从1开始编号？当然从第6、7页开始是同理啦。

子宫内膜癌研究论文【关键词】子宫内膜癌误漏诊子宫内膜癌是妇科生殖道最常见的恶性肿瘤之一。

发病率呈逐年上升趋势［１］，该病与其他妇科良性疾病不易鉴别，尤其是子宫内膜癌合并其他妇科疾病时，极易出现误、漏诊。

本院1997年1月至2007年12月共收治子宫内膜癌193例，其中误、漏诊10例，分析如下。

1临床资料1.1一般资料本组10例患者，年龄39～74岁。

术前诊断子宫肌瘤、卵巢肿瘤各3例，卵巢肿瘤合并子宫肌瘤、子宫腺肌症合并子宫肌瘤、宫内膜瘤样病变、功能性出血各1例。

临床表现：阴道出血8例；其中绝经后阴道出血4例、月经周期不规则3例、绝经前阴道不规则出血1例；因阴道排液、下腹痛并自扪及腹部包块就诊各1例。

1.2方法、结果本组术中行快速切片确诊3例、术后确诊7例。

术前诊断为子宫肌瘤3例,术前均未做诊刮,2例术中剖视子宫肉眼可疑内膜病变,送快速冷冻切片,病理检查示子宫内膜癌,行子宫次广泛切除术+双附件切除术。

术前诊断为卵巢恶性肿瘤可能3例,未行诊刮,均行子宫广泛切除术+双附件+大网膜切除术+阑尾切除术,术后病理检查示子宫内膜癌转移至卵巢。

1例术前卵巢肿瘤合并子宫肌瘤,术前未做诊刮,术中左附件送快速切片,病理检查示子宫内膜样腺癌,行全子宫切除术+双附件切除+大网膜切除术。

术前诊断子宫腺肌瘤合并子宫肌瘤1例,术前未做诊刮,,行全子宫切除术,术中送快速切片,病理检查示宫内膜腺体复杂型增生,术后病理检查:宫内膜中分化腺癌。

1例为宫内膜瘤样病变,诊刮病理检查:宫内膜腺体重度不典型增生,行全子宫切除术+双附件切除术,术后病理检查:宫内膜低分化腺癌,部分未分化癌浸润浅肌层。

术前诊断功能性出血1例,诊刮病理检查：子宫内膜复杂型增生,行全子宫切除术,术中送快速切片,病理检查示宫内膜腺体复杂型增生,术后病理检查示子宫内膜复杂型增生过长,灶区癌变浸润浅肌层。

2讨论2.1误、漏诊原因分析(1)先入为主,由于存在较明确子宫肌瘤、子宫腺肌病等疾病,未进一步考虑合并子宫内膜增生致癌变的可能。

海淀区2024年七年级增值评价基线调研数 学注意事项1. 本调研卷共 6 页，共3道大题，26道小题。

满分100分。

调研时间 90 分钟。

2. 在答题纸上准确填写姓名、学校名称和准考证号，并将条形码贴在指定区域。

3. 答案一律填涂或书写在答题纸上，在调研卷上作答无效。

4. 在答题纸上，选择题用2B铅笔作答，其他题目用黑色字迹的签字笔作答。

5. 调研结束，请将答题纸交回。

一、选择题（本题共30分，每小题3分）1．−12的相反数是A．12B．−12C．2 D．-22． 稀土是钪、钇、镧系17种元素的总称，素有“工业味精”之美誉，是我国重要的战略矿产资源．2024年我国稀土勘探在四川凉山取得新突破，预期新增稀土资源量496万吨．将4 960 000用科学记数法表示为A．0.49610×7B．49.610×5C．4.9610×7D．4.9610×63．下列计算正确的是A．（-5） + （-2）＝7 B．（-5） - （-2）＝3C．（-5）×（-2）＝-10 D．（-5）÷（-2）＝5 24．若x和y成反比例关系，当x的值分别为2，3时，y的值如下表所示，则表中a的值是x23y a4A．2 B．4 C．6 D．85．将下列各数在数轴上表示，其中与原点距离最近的点表示的数是A．-3 B．-0.8 C．1 D．26．对于多项式2x xy−，下列说法正确的是A．次数是2 B．一次项是2C．二次项系数是1 D．其值不可能等于22024. 117． 某文具原价为每件m 元，为迎接开学季，每件降5元，在此基础上新生还可以享受九折优惠. 一名新生购买一件该文具付款n 元，则n ＝A．0.9 （m -5） B．0.9m -5C．0.9mD．0.1 （m -5）8．若2s -4t ＝9，则s t −+212的值为A．10B．9.5C．5D．-49．若有理数a ，b 在数轴上的对应点的位置如图所示.下列结论中正确的是A．-a ＜b B．ab ＞1C．a b −＝b -aD．|2|a +＞|2|b −10． 关于x ，y 的单项式，若x 的指数与y 的指数是相等的正整数，则称该单项式是“等次单项式”，如x 2y 2，-3xy .给出下面四个结论：①-2x 3y 3是“等次单项式”；②“等次单项式”的次数可能是奇数；③两个次数相等的“等次单项式”的和一定是“等次单项式”；④若五个“等次单项式”的次数均不高于8，则它们中必有同类项.上述结论中，所有正确结论的序号是A．①③ B．①④C．②③D．②④二、填空题（本大题共18分，每小题3分）11． 在游乐场的“旋转茶杯”项目中，游客可以通过转动茶杯的方向盘自主控制茶杯的旋转方向.如果把逆时针旋转两圈记作+2，那么顺时针旋转三圈可以记作 ．12．比较大小：-1 −23．（填“＜”“＝”或“＞”）13． 约1500年前， 我国古代伟大的数学家和天文学家祖冲之计算出圆周率应在3.1415926和3.1415927之间，成为世界上第一个把圆周率的值精确到小数点后7位的人. 用四舍五入法将圆周率精确到千分位，所得到的近似数为 ．14． 多项式x y xy 2+2与一个整式的和是单项式，则这个整式可以是 ．（写出一个整式即可）15．若有理数m ，n 满足||m +（2-n ）4＝ 0，则m -n ＝ ．16．A ，B ，C ，D ，E 是圆上的5个点，在这些点之间连接线段，规则如下：ABC DE如图，已连接线段AB ，BC ，CD ，DE .（1）若想增加一条新的线段，共有 种连线方式；（2）至多可以增加 条线段.三、 解答题（本大题共52分，第17题3分，第18题12分，第19题6分，第20-24题，每小题4分，第25题5分，第26题6分） 解答应写出文字说明、演算步骤或证明过程.17．如图，数轴上点A 表示的数是-4，点B 表示的数是3．（1）在图中所示的数轴上标出原点O ；（2）在图中所示的数轴上表示下列各数，并将它们按从小到大的顺序用“＜”连接起来．-3，0，-1，2.5.18．计算：（1）2 - （-1）+（-6）； （2）-12×4÷（-2）；（3）（-103）×（2.5 -52）；（4）（-2）3−−+÷|2|94（−23）2.19．化简：（1）−+−23m n nm m n 222； （2）5[52()]a a a a 22−+−.20．先化简，再求值：11312323x x y x y −−+−+2()()22，其中x ＝13，y ＝-1.21．如图，正方形ABCD 的边长为a .（1）根据图中数据，用含a ，b 的代数式表示阴影部分的面积S ；（2）当a ＝6，b ＝2时，求阴影部分的面积.22． A I（人工智能）技术有望为传统的教学方式带来新变化，如AI 解题. 某公司为测验其AI 产品的解题能力，尝试利用最新考试题进行全科目测试. 分数记录以60分为基准，超过基准的分数记为正数，少于基准的分数记为负数. 将测试的相对分数记录如下:科目语文数学英语道法地理历史物理化学生物相对分数+20-16+30+28+8-9-18-9已知该AI 产品的地理测试分数为81分.（1）请补全上表；（2）在本次测试的各科目中，该产品所得最高分为 分，最低分为 分；（3）求该产品在本次测试中全科目的总分.23． “圆楼之王”承启楼位于福建省龙岩市，始建于明崇祯年间，是永定客家土楼群的组成部分.整座楼造型奇特，三环主楼环环叠套. 如图，中心位置耸立着一座祠堂．第三环楼为单层，有m 间房间；第二环楼为两层，每层的房间数均比第三环楼的房间数多8间；外环楼为四层，每层的房间数均等于第二环楼每层的房间数与第三环楼的房间数之和．（1） 第二环楼每层有 间房间，外环楼共有 间房间；（用含m 的式子表示）（2） 民间流传一首顺口溜：“高四层，楼四圈，上上下下间；圈套圈，圆中圆，历经沧桑数百年”.“”处所填内容是三环主楼所有房间数之和，已知m ＝32，求“”处所填的数.24. 小云和小明参加了数学节活动的某游戏，一次玩法如下：若S 1＜S 2，则小云获胜；若S 1＞S 2，则小明获胜；若S 1＝S 2，则双方平局. （1）若给定的有理数是2，小云为了确保自己获胜，则a 的值应该是 ；（2）若给定的有理数是2，4，则小云 确保自己获胜；（填“能”或“不能”）（3） 若给定的有理数是-2，0，2，4.当a 是负数，且双方平局时，则b ＝ .（用含a的式子表示）25． 对有理数a ，b 进行如下操作：第一次，将a ，b 中的一个数加1或者减1，另一个数加2或者减2，得到数a 1和b 1；第二次，将a 1和b 1中的一个数加1或者减1，另一个数加2或者减2，得到数a 2和b 2；…；第n 次，将a n -1和b n -1中的一个数加1或者减1，另一个数加2或者减2，得到数a n 和b n .（1）a ＝1，b ＝3.① 若a 1＝0，则b 1的值可以是 ； ② a b 22+所有可能的取值为 ；（2）若a n ＝a ，b n ＝b ，则n 的值是否可以是5？请说明理由.26． 给定有理数a ，b ，对整式A ，B ，定义新运算“⊕”：A B ⊕＝aA + bB ；对正整数n （n ≥2）和整式A ，定义新运算“⊗”：n ⊗A ＝ A A A ⊕⊕⊕n A个 （按从左到右的顺序依次做“⊕”运算），特别地，1⊗A ＝A .例如，当a ＝1，b ＝2时，若A ＝x ，B ＝-y ，则A B ⊕＝A + 2B ＝x - 2y ，2⊗A ＝A A ⊕＝3x .（1）当a ＝２，b ＝1时，若A ＝x + y ，B ＝x - 2y ，则A B ⊕＝ ，3⊗A ＝ ；（2）写出一组a ，b 的值，使得对每一个正整数n 和整式A ，均有n A ⊗＝A ， 并说明理由；（3） 当a ＝２，b ＝1时，若A ＝3x 2 + 7xy ，B ＝2x 2 - 30xy - y 2，p ，q 是正整数，令P ＝p A ⊗，Q ＝q B ⊗，且P Q ⊕不含xy 项，直接写出p 和q 的值.海淀区2024年七年级增值评价基线调研数学试题参考答案一、选择题（本题共30分，每小题3分）二、填空题（本大题共18分，每小题3分）11. 3− 12.<13. 3.14214.2xy −（答案不唯一）15. 2−16. 3; 2注：16题第一空1分，第二空2分三、解答题（本大题共52分，第17题3分，第18题12分，第19题6分，第20-24题，每小题4分，第25题5分，第26题6分） 17. 解：…………2分310 2.5−<−<< …………3分18. 解：（1）2(1)(6)−−+−21(6)=++− 3(6)=+−3=− …………3分（2）124(2)−⨯÷−48(2)=−÷−24=…………3分（3）法1：102()(2.5)35−⨯− 1052()()325=−⨯−105102()()()3235=−⨯+−⨯−25433=−+ 7=− …………3分法2：102()(2.5)35−⨯− 10()(2.50.4)3=−⨯− 10() 2.13=−⨯7=− …………3分（4）3242(2)|2|()93−−−+÷− 498294=−−+⨯821=−−+9=− …………3分19. 解：（1）n m nm n m 22232−+−n m 2132）（−+−=0= …………3分（2）225[52()]a a a a −+−)225522a a a a −+−=（)27522a a a −−=（22275a a a +−=a a 772−= …………3分20. 解：)3123()31(22122y x y x x +−+−− 22312332221y x y x x +−+−= ）（）（22313223221y y x x x ++−−= 23x y =−+ …………3分当13x =，1y =−时， 原式21(3)(1)1103=−⨯+−=−+=. …………4分21. 解：（1）21143()22S a b a b =−⋅−⨯−=233222a b a b −−+=23122a ab −− …………3分（2）当6a =，2b =时, 23166222S =−⨯−⨯=3691−−=26 …………4分 答：阴影部分的面积为26.22．解：（1）21+； …………1分（2）90；42； …………3分 （3）609(20)(16)(30)(28)(21)(8)(9)(18)(9)595⨯+++−+++++++++−+−+−=． 答：全科目的总分为595分. …………4分23. 解：（1）(8)m +；(832)m +； …………2分（2）2(8)4(28)1148m m m m ++++=+，当32m =时，原式=113248400⨯+=． …………4分 答：“*”处所填的数为400.24. 解：（1）2； …………1分（2）不能； …………2分 （3）2a −. …………4分25．解：（1）①1或5； ②2−，0，2，4，6，8，10； …………2分（2）n 不可能是5. 理由如下： …………3分由（1）②的分析知， 每次操作，两个数的和的变化量只能是1±或3±，都是奇数. 5次操作后，和的变化量依然是奇数.若5a a =，5b b =，两个数的和不变，变化量为0，是偶数，矛盾. …………5分 所以n 不可能是5.26. 解：（1）3x ，77x y +； …………2分（2）1a =，0b =（答案不唯一，满足a ，b 都是有理数，且1a b +=即可）． …………3分理由如下：首先1A A ⊗=成立． 因为1a =，0b =，所以10A A A A A ⊕=⋅+⋅=，即2A A ⊗=． 对每一个大于2的正整数n ，()1n An An A A A A A A AA A A−⊗=⊕⊕⊕=⊕⊕⊕==⊕=个个所以对每一个正整数n ，均有n A A ⊗=． …………4分 （3）4p =，3q =． …………6分。

第1页 共4页 ◎ 第2页 共4页保密★启用前2022-2023学年度小学四年级第一学期语文期末质量分析试题一、书写 1．抄写句子，格式正确，字迹工整。

开始练习的时候，飞卫对纪昌说：“你要想学会射箭，首先应该下功夫练眼力。

你要牢牢地盯住一个目标，不能眨眼！” ______二、信息匹配 2．读准拼音▶（把正确的读音打“√”）豆荚（jiáqiá） 窗框（kuàng kuāng ） 洋溢（xì yì）三、选择题 3．下列注音有误的一项是（ ）A ．骨髓（suÍ） 开凿（záo ） 两败俱（j Ǜ）伤 B ．灌溉（gài ） 绅（shēn ）士 拜（ bài ）年 C ．琴键（jiàn ） 瓷砖（zhuān ） 药剂（jì ） D ．挨揍（zòu ） 巫（ wū ）婆 流淌（tǎng ） 4．《爬天都峰》一文告诉我们( )A ．在困难面前要有战胜困难的勇气和信心，在与人相处的过程中，要善于互相学习、互相鼓励、共同进步。

B ．爬天都峰是一件不容易的事情，我们只有充满信心、相互鼓励，才能顺利地爬到峰顶。

四、句型转换 5．按要求完成句子练习。

（1）“我又胖又美！”这粒豌豆说，“我胖得要爆裂开来了。

”（改为转述句） _________________________________________（2）我们靠弘扬中国精神来实现我们的中国梦。

（改为设问句）________________________________________（3）假如请你来做科技馆的解说员，你会怎样向游客介绍中国的科技成果呢？请仿照例句，结合图中的科技成果来说一说吧！例：那时没有电灯，没有电视，没有收音机，也没有汽车。

________________________________________五、修改病句 6．修改下面的语段。

注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡考试时间：90分钟，总分：1502024届广东省第一次学业水平考试（小高考）数学模拟卷分，上第I 卷（选择题）一、选择题：本大题共12小题，每小题6分，共72分.在每小题给出的四个选项中，只有一项是符合题目要求的.B．>1,D．0<<的顶点与原点重合，始边与轴的正半轴重合，点（）第II卷（非选择题）二、填空题：本大题共6小题，每小题6分，共36分.三、解答题：本大题共4小题，第19～21题各10分，第22题12分，共42分.解答需写出文字说明、证明过程和演算步骤.(1)求频率分布直方图中，的值；(2)估计该班学生数学成绩的平均分和中位数21．某市为鼓励居民节约用电，采用阶梯电价的收费方式，当月用电量不超过100度的部分，按0.4元/度收费；超过100度的部分，按0.8元/度收费.(1)若某户居民用电量为120度，则该月电费为多少元？(5分)(2)若某户居民某月电费为60元，则其用电量为多少度？(5分) 22．如图，在正方体BB−1111中，B=1.(1)求证：B//平面1B1；(4分)(2)求证：B1⊥平面1B1；(4分)(3)求直线1和平面1B1所成的角.(4分)参考答案：令0.8K40=60，解得：J125，故其用电量为125度.22．(1)证明见解析(2)证明见解析(3)30°【分析】（1）由线面平行的判定可证明；（2）先证明线线垂直，从而可得线面垂直；（3）由（2）可得∠B1即为所求的角，再解三角形即可.【详解】（1）证明：因为在正方体BB−1111中，可知B//11,而B⊄平面1B1，11⊂平面1B1，所以B//平面1B1.（2）证明：因为在正方体BB−1111中，可知11⊥平面B11，且B1⊂平面B11，所以11⊥B1，又因为B1、1是正方形B11的对角形，因此B1⊥1，又11∩1=1，且11,1⊂平面1B1，所以B1⊥平面1B1.（3）设B1与1的交点为，连接1，由（2）可知直线1和平面1B1所成的角为∠B1,且△B1为直角三角形，∠B1=90°，设正方体BB−1111棱长为2，可得B1=22,B=2，所以∠B1=30°，因此直线1和平面1B1所成的角为30°.。

第三单元测试卷1．我会填写复韵母。

2．我会找，我会分。

韵母整体认读音节：我会连。

3．我能把字和相应的拼音连在一起。

4．我能连字成词。

5．比一比，选择正确的韵母把音节补充完整，再加上声调。

nǎi niú（）nǎi liú（）qīn tín（）fēnɡ（）qīnɡtínɡ（）奶奶　妹妹　小桥　家　路灯　下雪9．每组中哪个词不是同一类？用“\”画掉。

（1）shān yánɡ méi huā lù mù mǎ lǎo hǔ参考答案：1．【详解】本题考查的是拼音的拼读规则。

复韵母，是由两个或三个元音结合而成的韵母。

这种复合元音并不是两个元音或三个元音的简单相加，而是一种新的固定的音组，在口、耳里与单元韵有同感，应把它们作为一个个语音整体。

复元音韵母简称复韵母，包括ai 、ei、ao、ou、ia、ie、iao、iou、ua、uo、uai、uei、üe，共十三个。

2．韵母：er ieüe en onɡ整体认读音节：yu yin yun ri yuan【详解】本题考查的是拼音的相关文学常识。

注意平时对拼音的积累和识记，在拼音中“韵母”是一个中国汉语音韵学术语，汉语字音中声母、字调以外的部分。

韵母有：a、o、e、i、u、ü、ai 、ei、ui 、ao、ou、iu 、ie 、üe、er、an 、en 、in、un 、ün 、ang 、eng、ing 、ong。

其中，以上的24个韵母又分为单韵母和复韵母，单韵母是a、o、e、i、u、ü；复韵母是ai 、ei、ui 、ao、ou、iu 、ie 、üe、er、an 、en 、in、un 、ün 、ang 、eng、ing 、ong整体认读音节有16个，分别是：zhi 、chi、shi、ri、zi、ci、si、yi、wu、yu、ye、yue、yuan、yin 、yun、ying3．【详解】本题考查的是汉字的读音识记。

成都市2017级高中毕业班第一次诊断性检测数学（理科）本试卷分选择题和非选择题两部分。

第1卷（选择题）1至2页，第lI卷（非选择题）3至4页，共4页，满分150分，考试时间120分钟。

注意事项：1. 答题前，务必将自己的姓名考籍号填写在答题卡规定的位置上。

2. 答选择题时，必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦千净后，再选涂其它答案标号。

答非选择题时，必须使用05毫米黑色签字笔，将答案书写在答题卡规定的位置上。

4. 所有题目必须在答题卡上作答，在试题卷上答题无效。

5. 考试结束后，只将答题卡交回。

第1卷（选择题，共60分）一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1若复数Z 1与Zz =-— (i 为虚数单位）在复平面内对应的点关于实轴对称，则Z1=CA)-—i (B)-3+ (C)+i (D)—!2.已知集合A={—1,0,m},B={l ,2}. 若A U B = {-1,0,1,2}, 则实数m的值为(A)-1或0(B)O或1CC)—1或23.若si n e =乔cos(2穴-0),则tan20=石乔瓦CA)——CB) -CC)—一 2 4.某校随机抽取100名同学进行“垃圾分类”的问卷测试，测试结果发现这100名同学的得分都在[50,100]内，按得分分成5组：[50,60), [60, 70), [70, 80),[80,90),[90,100], 得到如图所示的频率分布直方图则这100名同学的得分的中位数为CA )72. 50.040 0.030 数学（理科）”一诊“考试题第1页（共4页）CD)l或2CD)-污2 彗0.015 (B )75 0.0100.005 (C)77. 5(D)80。

工丑扫已。

100得分5设等差数列{a ,}的前n项和为S,,,且a ,,-::/:-0.若as =a 3, 则—＝s 9 S s 9 5 5 (A)了(B)了(C)了6已知a,/3是空间中两个不同的平面，m,n是空间中两条不同的直线，则下列说法正确的是(A)若m II a ,n II /3, 且a II /3,则m II n (B)若m II a ,n II /3, 且a_l/3,则m II n (C)若m_la ,n II /3, 且a II /3, 则m _l n (D)若m _la,n ll /3,且a_l/3,则m _l n7.(x 2+2)(x ——)6的展开式的常数项为(A)25(B)-25 (C)5(D )—5 8.将函数y =si n (4x -王）图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），再把所6 得图象向左平移王个单位长度，得到函数f(x)的图象，则函数f(x)的解析式为6 (A) f(x) =si n (2x +互）6 CA) C —2,0) LJ (2, 十=)穴CB) f(x) =si n (2x —一） 亢(C) f(x) =si n (8x +岊)(D) f(x) =si n (8x —一）9已知抛物线沪=4x 的焦点为F,M,N是抛物线上两个不同的点．若I M Fl+INFl =5,则线段MN的中点到y轴的距离为CA)3 3_2） B （ CC)5 10.巳知a =沪，b=3了，c =l n -2 ，则(A) a> b > c (B) a> c > b (C) b >a> c (D) b > c > a 11已知定义在R上的函数f(x)满足f(2-x)= f(Z +x), 当x冬2时，f(x)= (x —l)e< :--1 若关于x的方程f(x)-kx +zk —e +l=O 有三个不相等的实数根，则实数K的取值范围是(B)(—2,0) LJ (0,2)CC)C —e,O) U (e, 十oo)CD)C —e ,O) U (0, e ) 12.如图，在边长为2的正方形AP 1贮凡中，线段BC的端点B,C分别在边P1P 2,P 2P 3 _t 滑动，且P 2B =P心=x.现将丛AP 1B ,6AP 3C分别沿AB,A C折起使点P1,凡重合，重合后记为点P ,得到三棱锥P-ABC 现有以下结论：(DAP上平面PBC;＠当B,C分别为P1P2,P 2凡的中点时，三棱锥P —ABC的外接球的表面积为67(;®x 的取值范圉为(0,4—2迈）； 1 ＠三棱锥P —ABC体积的最大值为—.则正确的结论的个数为P 1 5_2、丿D （ A 27CD)一5 (A)l (B)2CC )3(D )4数学（理科）”一诊“考试题第2页（共4页）。

深圳外国语学校（集团）龙华高中部2025届高三年级第一次月考 数学试卷本试卷共4页，19小题，满分150分.考试用时120分钟. 注意事项：1．答卷前，考生务必用黑色字迹钢笔或签字笔将自己的姓名、考生号、考场号和座位号填写在答题卡上.用2B 铅笔将试卷类型（A ）填涂在答题卡相应位置上.将条形码横贴在答题卡右上角“条形码粘贴处”.2．作答选择题时，选出每小题答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上.3．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液.不按以上要求作答的答案无效.4．考生必须保持答题卡的整洁.考试结束后，将试卷和答题卡一并交回. 一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．设集合{}30xAx ex =−<，{}1,0,1,2B =−，则集合A B = （ ）A ．{}1,2−B ．{}1,1,2−C ．{}1,2D ．{}12．已知2i 1iz−=−+，则z =（ ） A ．1i +B ．1i −C ．3i −D ．3i + 3．已知向量(,1)a x = ，(2,1)b =− ，若()(2)a b a b +⊥−，则实数x =（ ）A ．2B ．12−C ．2−或4D ．44．已知3sin 24θ=−，则1tan tan θθ+=（ ）A ．43B ．12−C ．83D ．83−5．已知圆锥的底面半径为2，高为4，有一个半径为1的圆柱内接于此圆锥，则该圆柱的侧面积是（ ）A ．πB ．2πC ．3πD ．4π6．已知函数()122,0,,0,x x f x x x ≤= > 则下列说法正确的是（ ）A ．()f x 是R 上的增函数B ．()f x 的值域为[)0,∞+C ．“14x >”是“()12f x >”的充要条件D ．若关于x 的方程()f x a =恰有一个实根，则1a >7．已知函数π()sin(2)2f x x ϕϕ=+< 满足ππ43f f = ，若()f x 在区间π,2t上恰有3个零点，则实数t 的取值范围为（ ）A ．25π37π,2424B ．25π49π,2424C ．37π49π,2424D ．37π49π,24248．已知函数()y f x =具有以下的性质：对于任意实数a 和b ，都有()()()()2f a b f a b f a f b ++−=⋅，则以下选项中，不可能是()1f 值的是（ ） A ．2− B ．1− C ．0 D ．1二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．9．若随机变量()2~0,X N σ，()()f x P X x =≤，则（ ）A ．()()1f x f x −=− B ．()()22f x f x =C ．()()()210P X x f x x <=−> D ．若()121x f f x +> −，则113x << 10．已知三次函数()325(0)f x x bx b =++<有极小值点2x =，则下列说法中正确的有（ ）A ．3b =−B ．函数()f x 有三个零点C ．函数()f x 的对称中心为(1,3D ．过()1,1−可以作两条直线与()y f x =的图象相切11．数学中有许多形状优美，寓意美好的曲线，曲线22|:1|C x y x y +=+就是其中之一（如图）．给出下列四个结论，其中正确结论是（ ）A ．图形关于y 轴对称B ．曲线C 恰好经过6个整点（即横､纵坐标均为整数的点）C ．曲线C 的点D ．曲线C 所围成的“心形”区域的面积大于3 三、填空题：本题共3小题，每小题5分，共15分．12．已知12,F F 为椭圆2222:1(0)C b b x a a y +>>=的两个焦点，P 为椭圆C 上一点，且12PF F △的周长为6，面C 的离心率为 .13．已知函数32(),()f x x x g x x a =−=+，曲线()y f x =在点(1,(1))f −−处的切线也是曲线()y g x =的切线．则a 的值是14．有一道楼梯共10阶，小王同学要登上这道楼梯，登楼梯时每步随机选择一步一阶或一步两阶，小王同学7步登完楼梯的概率为 .四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．15．（13分）如图，一智能扫地机器人在A 处发现位于它正西方向的B 处和北偏东30°方向上的C 处分别有需要清扫的垃圾，红外线感应测量发现机器人到B 的距离比到C 的距离少0.4m ，于是选择沿A →B →C 路线清扫.已知智能扫地机器人的直线行走速度为0.2m /s ，忽略机器人吸入垃圾及在B 处旋转所用时间，10s 完成了清扫任务.(1)求B 、C 两处垃圾之间的距离；(2)求智能扫地机器人此次清扫行走路线的夹角B 的余弦值.16．（15分）已知双曲线2222:1(0,0)x y C a b a b −=>>的焦点与椭圆2215x y +=的焦点重合，其渐近线方程为y x =. (1)求双曲线C 的方程；(2)若,A B 为双曲线C 上的两点且不关于原点对称，直线1:3l y x =过AB 的中点，求直线AB 的斜率.17．（15分）如图，在四棱锥B ACDE －中，正方形ACDE 所在平面与正ABC 所在平面垂直，M N ，分别为BC AE ，的中点，F 在棱CD 上．(1)证明：//MN 平面BDE ．(2)已知2AB =，点M 到AF 求三棱锥C AFM －的体积．18．（17分）蓝莓种植技术获得突破性进展，喷洒A 型营养药有--定的改良蓝莓植株基因的作用，能使蓝莓果的产量和营养价值获得较大提升．某基地每次喷洒A 型营养药后，可以使植株中的80%获得基因改良，经过三次喷洒后没有改良基因的植株将会被淘汰，重新种植新的植株． (1)经过三次喷洒后，从该基地的所有植株中随机检测一株，求-株植株能获得基因改良的概率；(2)从该基地多个种植区域随机选取一个，记为甲区域，在甲区域第一次喷洒A 型营养药后，对全部N 株植株检测发现有162株获得了基因改良，请求出甲区域种植总数N 的最大可能值；(3)该基地喷洒三次A 型营养药后，对植株进行分组检测，以淘汰改良失败的植株，每组n 株(50)n ≤，一株检测费为10元，n 株混合后的检测费用为8n +元，若混合后检测出有未改良成功的，还需逐一检测，求n 的估计值，使每株检测的平均费用最小，并求出最小值．（结果精确到0.1元）附：当0.01a <，50n ≤时，()11nna a ≈++，*n N ∈.19．（17分）“函数()x ϕ的图象关于点(),m n 对称”的充要条件是“对于函数()x ϕ定义域内的任意x ，都有()(2)2x m x n ϕϕ+−=，若函数()f x 的图象关于点()12，对称，且当[]01x ∈，时，2()1f x x ax a =−++ (1)求(0)(2)f f +的值； (2)设函数4()2xg x x=− ①证明函数()g x 的图象关于点(2,4)−称；②若对任意[]10,2x ∈，总存在22,13x∈−，使得()()12f x g x =成立，求实数a 的取值范围.数学参考答案：1．D【详解】解：将B 中元素分别代入30x e x −<，只有1符合，则{}1A B ∩=. 故选：D. 2．B 【详解】2i 21i 1i 1izz z −=−⇒−=−⇒=++， 所以1i z =−. 故选：B ． 3．C【详解】由题设(2,0)a b x +=+ ，2(4,3)a b x −=−， 所以()(2)(2)(4)0a b a b x x +⋅−=+−=，可得x =2−或4.故选：C 4．D【详解】3sin 22sin cos 4θθθ==− ，3sin cos 8θθ∴=−，221sin cos sin cos 18tan 3tan cos sin sin cos 38θθθθθθθθθθ+∴+=+===−−. 故选：D. 5．D【详解】如图，设圆柱的高为h ，由题意可得142h =，所以2h =，从而圆柱的侧面积2124S ππ=××=侧，故选：D.6．D【详解】对于A ，当0x =时，102210=>，所以()f x 不是R 上的增函数，所以A 错误， 对于B ，当0x ≤时，021x <≤，当0x >时，120x >， 所以()f x 的值域为(0,)+∞，所以B 错误， 对于C ，当0x ≤时，由()12f x >，得122x >，解得10−<≤x ，当0x >时，由()12f x >，得1212x >，解得14x >，综上，由()12f x >，得10−<≤x ，或14x >，所以“14x >”是“()12f x >”的充分不必要条件，所以C 错误，对于D ，()f x 的图象如图所示，由图可知当1a >时，直线y a =与()y f x =图象只有一个交点， 即关于x 的方程()f x a =恰有一个实根，所以D 正确， 故选：D 7．C【详解】由题意可知，()f x 的最小正周期2ππ2T ==， 因为πππ34124T−=<，可知ππ7π34224x +=为()f x 的一条对称轴， 所以()f x 在7π24x =之后的零点依次为7π13π24424T +=，7π325π24424T +=，7π537π24424T +=，7π749π24424T +=，…， 若()f x 在区间π,2t上恰有3个零点，所以37π49π2424t ≤<. 故选：C. 8．A【详解】因为函数()y f x =对于任意实数a 和b ，都有()()()()2f a b f a b f a f b ++−=⋅，所以令0a b ==，有()()()()00200f f f f +=⋅，即()()20[01]0f f −=，所以()00f =或()01f =；令2x a b ==，x 为任意实数，有()()0222x x f x f f f +=⋅ ，即()()2022x x f x f f f⋅−； 因为022x x f f⋅≥，所以()()0f x f ≥−，当()00f =时，()0f x ≥；当()01f =时，()1f x ≥−； 所以()f x 的值不可能是2−， 故选：A. 9．ACD【详解】对于A ，随机变量()2~0,X N σ满足正态分布，且0µ=，故()()()()1f x P X x P X x f x −=≤−=≥=−，故A 正确； 对于B ，当0x =时，()()()(),20212201,f x P X f x P X =≤=≤== 此时()()22f x f x ≠，故B 错误；对于C ，()()()20P X x P x X x P X x <=−<<=<<()()12212f x f x=−=−，故C 正确；对于D ，()()f x P X x =≤，故()f x 单调递增，故()121x f f x +> −，即121x x +>−， 解得113x <<，故D 正确. 故选：ACD 10．ACD【详解】()232f x x bx ′=+， 因为函数()325(0)f x x bx b =++<有极小值点2x =，所以()21240f b ′=+=，解得3b =−，所以()3235f x x x =−+，()236f x x x ′=−， 当2x >或0x <时，()0f x '>，当02x <<时，()0f x ′<， 所以函数()f x 在()(),0,2,−∞+∞上单调递增，在()0,2上单调递减，所以()()()()05,21f x f f x f ====极大值极小值， 又()215f −=− 所以函数()f x 仅有1个在区间()2,0−上的零点，故A 正确，故B 错误；对于C ，由()()3223535f x x x x x =−+=−+，得()()()()()()2211113511356f x f x x x x x ++−=++−++−−−+=， 所以函数()f x 的图象关于()1,3对称，故C 正确；对于D ，设切点为()32000,35x x x −+，则()200036f x x x =−′， 故切线方程为()()()320020003365y x x x x x x −−+−−=，又过点()1,1−，所以()()()3200200315163x x xx x −−−+=−−，整理得300320x x −−=，即()()200120x x +−=， 解得01x =−或02x =，所以过()1,1−可以作两条直线与()y f x =的图象相切，故D 正确. 故选：ACD.11．ABD【详解】对于A ，将x 换成x −方程不变，所以图形关于y 轴对称，故A 正确； 对于B ，当0x =时，代入可得21y =，解得1y =±，即曲线经过点(0,1),(0,1)−，当0x >时，方程变换为2210y xy x −+−=，由224(1)0x x ∆=−−≥，解得x ∈ ，所以x 只能取整数1，当1x =时，20y y −=，解得0y =或1y =，即曲线经过(1,0),(1,1)， 根据对称性可得曲线还经过(1,0),(1,1)−−，故曲线一共经过6个整点，故B 正确；对于C ，当0x >时，由221x y xy +=+可得222212x y x y xy ++−=≤，（当x y =时取等号），222x y ∴+≤，C 上y称性可得：曲线C ，故C 错误；对于D ，如图所示，在x 轴上图形的面积大于矩形ABCD 的面积：1122S =×=，x 轴下方的面积大于等腰三角形ABE 的面积：212112S =××=，所以曲线C 所围成的“心形”区域的面积大于213+=，故D 正确； 故选：ABD12．12/0.5【详解】依题意，12PF F △的周长为226a c +=，所以123,a c PF F +=面积的最大值为122c b bc ××又222a b c =+，整理得2223(3)c c c−=+,即2(1)(21)0c c −+=,解得1,2,===c a b C 的离心率为12，故答案为：12 13．3【详解】由题意知，(1)1(1)0f −=−−−=，2()31x f x ′=−，(1)312f ′−=−=， 则()y f x =在点()1,0−处的切线方程为2(1)y x =+， 即22y x =+，设该切线与()g x 切于点()00,()x g x ， 其中()2g x x ′=，则00()22g x x ′==，解得01x =， 将01x =代入切线方程，得2124y =×+=， 则(1)14g a =+=，解得3a =； 故答案为：3 14．3589【详解】解：由题意可分为5步、6步、7步、8步、9步、10步共6种情况，①5步：即5步两阶，有551C =种；②6步：即4步两阶与2步一阶，有2615C =种；③7步：即3步两阶与4步一阶，有3735C =种；④8步：即2步两阶与6步一阶，有2828C =种；⑤9步：即1步两阶与8步一阶，有199C =种；⑥10步：即10步一阶，有10101C =种；综上可得一共有89种情况，满足7步登完楼梯的有35种； 故7步登完楼梯的概率为3589故答案为：358915．(1)()1.4m (2)1114【详解】（1）由题意得0.2102AB BC +=×=，设BC x =，02x <<，则2AB x =−，20.4 2.4AC x x =−+=−，由题意得9030120A=°+°=°. 在ABC 中，由余弦定理得222cos 2AB AC BC A AB AC+−=× ()()222(2)(2.4)122 2.42x x x x x −+−−==−×−×−， 解得 1.4x =或5.2（舍去）， ∴()1.4m BC =（2）由（1）知62 1.0.4AB =−=， 2.4 1.41AC =−=， 1.4BC =. ∴2222220.6 1.4111cos 220.6 1.414AB BC AC B AB BC +−+−===⋅××. 16．(1)2213x y −= (2)1 【详解】（1）椭圆2215x y +=的焦点为()2,0±，故224a b +=，由双曲线的渐近线为y =，故b a =1,b a ==故双曲线方程为：2213x y −=. （2）设()()1122,,,A x y B x y ，AB 的中点为M ，因为M 在直线1:3l y x =，故13M M y x =， 而121231y x −=，222231y x −=()()12120y y y y −+=， 故()()121203M M x x x y y y −−−=， 由题设可知AB 的中点不为原点，故0M M x y ≠，所以121213M M y y xx x y −==−， 故直线AB 的斜率为1.此时12:33M M M AB y x x x x x =−+=−， 由222333M x y x x y =− −=可得222333M x x x −−= ，整理得到：22424303M M x x x x −++=， 当222416Δ168324033M M M x x x =−+=−>即M x <M x >即当M x <M x >AB 存在且斜率为1. 17．(1)证明见解析；(2)【详解】（1）取CD 中点G ，连接NG ，MG,G M 为,CD BC 中点 //GM BD ∴又BD ⊂平面BDE ，GM ⊄平面BDE //GM ∴平面BDE四边形ACDE 为正方形，,N G 为,AE CD 中点 //NG DE ∴又NG ⊂平面BDE ，NG ⊄平面BDE //NG ∴平面BDEGM NG G = ，,GM NG ⊂平面MNG ∴平面//MNG 平面BDE又MN ⊂平面MNG //MN ∴平面BDE（2）ABC ∆ 为正三角形，M 为BC 中点 AM BC ∴⊥平面ACDE ⊥平面ABC ，CD AC ⊥，平面ACDE 平面ABC AC =，CD ⊂平面ACDE CD 平面ABC ，又AM ⊂平面ABC AM CD ∴⊥又BC CD C ∩=，,BC CD ⊂平面BCD AM ∴⊥平面BCD FM ⊂ 平面BCD AM MF ∴⊥设CF a =，则AF =MF =，AM =AF AM MF ∴=⋅=1a =11111332C AFM A FCM FCM V V S AM −−∆∴==⋅=×××=18．(1)0.992(2)202株(3)10n =，2.6元 【详解】（1）记事件A =“该基地的植株经过三次喷洒后，随机检测一株植株能获得基因改良”，所以2()0.80.20.80.20.80.992P A =+×+×=，（2）因为植株经过一次喷洒后基因改良的概率为0.8，经过一次喷洒后基因改良的株数k 服从二项分布，()C 0.80.2k k N k N P N k −⋅==，0,1,2,,k N = 当162k <时，()1620Pk == 当162k ≥时，设162162162(162)C 0.80.2N N P k −==⋅ 若162N =时，则()()162161P k P k =<=若162N >时，则16216216216216216111621621621621621631C 0.80.2C 0.80.2C 0.80.2C 0.80.2N N N N N N NN −−+−−− ≥ ≥ ，所以0.8161.20.8162N N ≥ ≤ ， 解得201.5202.5N ≤≤，又*N N ∈，所以202N = 所以甲区域种植总数N 的最大可能值为202株． （3）设每组n 株(50)n ≤的总费用为X 元，则X 的取值为8n +，118n + 所以 X8n + 118n +P 0.992n 10.992n −所以()(8)0.992(118)(10.992)n n E X n n =+++− (8)0.992(118)(10.992)n nn n n+++−= 所以()811100.992n E X n n=−×+ 因为()0.99210.00810.008n n n =−≈− 所以()810.081 2.6E X n n n =++≥+=（当且仅当10n =时等号成立） 所以当以10个每组时，检测成本最低，每株2.6元．19．(1)4【详解】（1）由题意可得，()(2)224f x f x +−=×=，令0x =，可得(0)(2)4f f +=. （2）①由4()2x g x x=−，(,2)(2,)x ∈−∞+∞ ， 44(4)()(4)22(4)x x g x g x x x −+−=+−−−416422x x x x−−−−8162x x −=−8=−2(4)=×−， 所以函数()g x 的图象关于点(2,4)−对称.②4()2x g x x =−842x =−+−，函数在2,13 − 上单调递增，所以[]()1,4g x ∈−， 不妨设()f x 在[]0,2上的值域为A ，则[]1,4A ⊆−，因为[]01x ∈，时，2()1f x x ax a =−++， 所以(1)2f =，即函数()f x 的图象过对称中心()12，， （i ）当02a ≤时，即0a ≤，函数()f x 在[]0,1上单调递增， 由对称性可知，()f x 在[]1,2上单调递增，所以()f x 在[]0,2上单调递增，由(0)1f a =+，(0)(2)4f f +=，所以(2)3f a =−，所以[]1,3A a a =+−， 由[]1,4A ⊆−，可得114313a a a a +≥− ≥− +≤−，解得10a −≤≤； （ii ）当012a <<时，即02a <<，函数()f x 在0,2a上单调递减，()f x 在,12a 上单调递增，由对称性可知，()f x 在1,22a − 上单调递增，()f x 在2,22a −上单调递减， 所以()f x 在0,2a 上单调递减，在,222a a − 上单调递增，在2,22a − 上单调递减， 结合对称性可得，[](2),(0)A f f = 或(),(2)22a a A f f =− ， 因为02a <<，所以(0)1(1,3)f a =+∈，(2)3(1,3)f a =−∈， 易知2()1(1,2)24a a f a =−++∈，又()(2)422a a f f +−=，所以(2)(2,3)2a f −∈， 所以当02a <<时，[]1,4A ⊆−成立； （iii ）当12a ≥时，即2a ≥时，函数()f x 在[]0,1上单调递减， 由对称性可知，()f x 在[]1,2上单调递减，所以函数()f x 在[]0,2上单调递减，又(0)1f a =+，(2)3f a =−，则[]3,1A a a =−+，由[]1,4A ⊆−得， 311431a a a a −≥− +≤ −≤+，解得23a ≤≤. 综上可知，实数a 的取值范围为[]1,3−.。

---------------------------------------------------------------最新资料推荐------------------------------------------------------第1页共4 页第 1 页共 4 页三峡大学 2006 年研究生入学考试试题考试科目：生物综合（考生必须将答案写在答题纸上）一. 名词解释: （每小题 4 分, 共 32 分） 1. 世代交替：2. 后口动物：3. 食物链：3. 细胞全能性：4. 遗传平衡定律：5. 物种:6. 菌落：7.朊病毒：8.局限转导：二. 选择题: （每小题 1 分, 共 25 分） 1. 生物多样性通常分为（）三个层次。

（A）生态环境多样性（B）生态系统多样性（C）物种多样性（D）遗传多样性 2．早期单细胞生物的进化，包括（）等几个时期（按进化的时间顺序填写）。

（A）最早的生活细胞（B）产氧的光合自养细胞（C）自养细胞（D）耐氧和好氧细胞出现（E）真核细胞第 2 页3. 下列不属于高等植物细胞中的是：1 / 4（） A、细胞壁 B、质膜 C、核糖体 D、中心体 4．动物所需的营养物质共有六类，其中（）是能源物质。

（A）糖（B）脂肪（C）蛋白质（D）水（E）维生素（F）矿物质 5、 Pseudomonas transluces、 Pseudomonas syringae、 Pseudomonas propanica 是相同( )的生物。

（A）目（B）科（C）属（D）种 6、下列哪些生物是原核生物（）（A）病毒（B）细菌（C）肉足虫（D）鞭毛虫 7、哪些生物不具有细胞结构（）（A）病毒（B）蓝细菌（C）放线菌（D）鞭毛虫 8、（）是裸子植物的特征。

（A）胚珠裸露（B）木质部具筛管（C）双受精现象（D）形成果实 9、下列对被子植物描述不正确的有（）。

（A）具有典型的根、茎、叶、花、果实、种子（B）可以分为单子叶植物和双子叶植物（C）子房发育成果实（D）松树、紫荆都是被子植物 10、循环系统最先在（）中出现（A）腔肠动物（B）节肢动物（C）鱼类（D）环节动物（E）软体动物 11、呼吸系统最先在（）中出现（A）腔肠动物（B）节肢动物（C）鱼类（D）环节动物（E）软体动物 12、脊索动物具有（）等基本特征（A）脊索（B）神经索（C）鳃裂（D）神经管第 3 页 13. 所有生态系统都可以区分为四个组成成分，即生产者、消费者、分解---------------------------------------------------------------最新资料推荐------------------------------------------------------ 者和（）。

一、工作场所空气有毒物质测定—臭氧检测作业指导书臭氧的溶液吸收-丁子香酚分光光度法1适用范围本作业指导书规定了工作场所空气中臭氧的溶液吸收-丁子香酚分光光度法，适用于工作场所空气中的臭氧的浓度检测。

2引用标准GBZ/T 300.48-2017 工作场所空气有毒物质测定第48 部分：臭氧和过氧化氢3 工作目的与要求3.1 确保操作人员的职业健康安全、设备财产安全和环境安全；3.2 熟知、熟练运用本指导书内容并严格执行。

4工作原理及条件4.1 原理空气中臭氧与丁子香酚反应生成甲醛，甲醛与二氯亚硫酸汞钠及盐酸副玫瑰苯胺反应生成紫红色化合物，用分光光度计在560 nm 波长下测定吸光度，进行定量。

4.2 仪器4.2.1 大气泡吸收管。

4.2.2 空气采样器，流量范围为0 L/min～5 L/min。

4.2.3 具塞比色管，10 mL。

4.2.4 恒温水浴箱。

4.2.5 分光光度计，具1 cm 比色皿。

4.3 试剂4.3.1 实验用水为蒸馏水，试剂为分析纯。

4.3.2 丁子香酚（4-烯丙基-2-甲氧基苯酚）：临用前，通过亚硫酸钠结晶柱（6 mm×80 mm）提纯。

4.3.3四氯汞钠溶液：1.36 g 氯化汞和 0.58 g 氯化钠溶于 100 mL 水中。

4.3.4 二氯亚硫酸汞钠溶液：0.12 g 无水亚硫酸钠溶于100 mL 四氯汞钠溶液中，应在24 h内使用。

4.3.5 盐酸副玫瑰苯胺溶液：0.16 g 盐酸副玫瑰苯胺溶于24 mL 盐酸（ρ＝1.18 g/mL）中，加水至100 mL。

204.3.6 标准溶液：取2.8 mL 甲醛（含量36％～38％），用水稀释至1000 mL。

标定后，稀释成100.0µg/mL 标准贮备液。

置于冰箱内保存可使用3 个月。

临用前，用水稀释成5.0µg/mL甲醛标准溶液。

或用水稀释国家认可的甲醛标准溶液配制。

5 样品的采集、运输和保存现场采样按照GBZ 159 执行。

第1页共4页第2页共4页2022-2023学年度第一学期四年级语文学期综合素养评价（B ）（考试时间为80分钟，满分100分）第一部分积累运用（41分）一、读拼音，将汉字有序地写在田字格内。

（10分）体育课后，他倍感píláo，很不shūfu ，jīng pílìjié，走路也摇晃，感觉天在xuán zhuǎn ，同学们立刻扶着他去医务室。

二、选择正确的选项。

（12分）1．下列加点字的读音完全正确的一项是（）。

A ．角．色（jué）宁．可（níng ）B ．霎．时（chà）暖和．（huo ）C ．灌溉．（gài ）哄．笑（hōng ）D ．露．脸（lù）分．量（fèn ）2．给下面句子选择恰当的词语，正确的一项是（）。

小哪吒生得______，脚踩风火轮，手持混天绫，真是______。

A ．慈眉善目威风凛凛B ．威风凛凛眉清目秀C ．眉清目秀威风凛凛D ．威风凛凛慈眉善目3．小华在做数学题的时候，常把小数点的位置弄错，他却认为这不是多大的事。

我们可以用下面的哪句话提醒他？（）A ．差之毫厘，谬以千里。

B ．比上不足，比下有余。

C ．机不可失，时不再来。

D ．尺有所短，寸有所长。

4．选择正确的字词填空。

（填序号）（4分）A ．赔B ．培（1）（）育新品种水果的失败导致他（）了不少钱。

A ．打头阵B ．碰钉子（2）这场比赛（）的是小明，由于经验不足，他容易在比赛中（）。

5．写某个事物的观察日记时，要进行（）观察，才能写得准确。

A ．粗略的B ．马虎的C ．细致的D ．详细的三、阅读文段，完成句子练习。

（6分）①夏天，我们喜欢爱在湖边打水漂，看石片在水里钻进钻出。

②我们还经常举行游泳比赛，不管自由式，还是狗刨式，只要游在前头，就是冠军。

③秋天，丰收的场院非常热闹。

④我们一会儿在草堆里捉迷藏，一会儿_______________________，一会儿_________________________。

2024年新高考改革适应性练习（3）（九省联考题型）数学试题卷（2024.2.6）考生须知1. 本卷共4页，四大题19小题，满分150分，答题时间120分钟；2. 答题时须在答题卡上填涂所选答案（选择题），或用黑色字迹的签字笔规范书写答案与步骤（非选择题），答在本试题卷上或草稿纸上的答案均属无效；3. 考试结束时，考生须一并上交本试题卷，答题卡与草稿纸．一、单项选择题（本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1. 设样本空间ΩΩ={1,2,…,6}包含等可能的样本点，且AA={1,2,3,4}，BB={3,4,5,6}，则PP(AABB)= A．13B．14C．15D．162. 若复数zz满足zz2是纯虚数，则|zz−2|的最小值是A．1 B．√2C．2 D．2√23. 算术基本定理告诉我们，任何一个大于1的自然数NN，如果NN不为质数，那么NN可以唯一分解成有限个素因数的乘积的形式．如，60可被分解为 22×31×51，45可被分解为 32×51．任何整除NN的正整数dd都叫作NN的正因数．如，20的正因数有1，2，4，5，10，20．则4200的正因数个数是A．4 B．7 C．42 D．484. 已知点(aa,bb)在直线 2xx+yy−1=0 第一象限的图像上，则1aa+1bb的最小值是A．3+2√2B．2+2√2C．1+2√2D．2√25. 已知函数ff(xx)=sin xx，gg(xx)=cos xx，则ff�gg(xx)�和gg�ff(xx)�都单调递增的一个区间是A．�2ππ5,4ππ5�B．�4ππ5,6ππ5�C．�6ππ5,8ππ5�D．�8ππ5,2ππ�6. 已知直线ll过点(2,1)，且与两坐标轴围成的三角形的面积是6，则满足条件的直线ll共有A．1条B．2条C．3条D．4条7. 我们记ff(nn)(xx)为函数ff(xx)的nn次迭代，即ff(1)(xx)=ff(xx)，ff(2)(xx)=ff�ff(xx)�，…，ff(nn)= ff�ff(nn−1)(xx)�．已知函数gg(xx)=xx|xx|，则gg(2024)(xx)=A．xx3|xx|2021B．xx4|xx|2020C．xx2|xx|2022D．xx20248. 若一四面体恰有一条长度大于1的棱，则这个四面体体积的最大值是A．√33B．12C．13D．√22二、多项选择题（本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，有选错的得0分，若只有2个正确选项，每选对一个得3分；若只有3个正确选项，每选对一个得2分．）9. 已知函数ff(xx)=xx3−2xx，下列说法正确的是A．函数gg(xx)=ff(xx)+ff′(xx)无零点B．直线 2xx+yy=0 与yy=ff(xx)相切C．存在无数个aa>0 ，ff(xx)在区间(−aa,aa)上不单调D．存在mm>0 ，使得对于任意nn，ff(nn)≤ff(nn+mm)10. 若一个人一次仅能爬1级或2级台阶，记aa nn为爬nn级台阶时不同的爬法数(nn∈NN∗)．关于数列{aa nn}，下列说法正确的是A．函数ff(nn)=aa nn单调递增B．aa1+aa3+aa5的值为12C．aa1+aa2+⋯+aa10=232D．2aa12+aa22+⋯+aa102=89×14411. 如右图，已知抛物线CC的焦点为FF，准线方程为ll:xx=−1 ，点PP是CC上的一动点．过点PP作ll的垂线，垂足为QQ．过点PP作CC的切线，该切线与xx,yy轴分别交于AA,BB两个不同的点．下列说法正确的是A．抛物线CC的标准方程为yy2=2xxB．QQ,BB,FF三点共线当且仅当|PPFF|=4C．当|PPFF|≠1 时，都有PPAA⊥QQFFD．当|PPFF|≠1 时，△PPAAFF恒为等腰三角形三、填空题（本题共3小题，每小题5分，共15分．）12. 在棱长为1的正方体AABBCCAA−AA1BB1CC1AA1中，三棱锥CC−AABB1AA1的体积是_________．13. 从集合{xx|−4≤xx≤2024}中任选2个不同的非零整数作为二次函数ff(xx)=aaxx2+bbxx的系数，则所有满足ff(xx)的顶点在第一象限或第三象限的有序数对(aa,bb)共有_________组．14. 已知向量aa,bb,cc满足aa+bb+cc=00，(aa−bb)⊥(aa−cc)，|bb−cc|=3 ，则|aa|+|bb|+|cc|的最大值是_________．四、解答题（本题共5小题，共77分．解答应写出文字说明，证明过程或演算步骤．）15.（13分）已知正方体AABBCCAA−AA1BB1CC1AA1．（1）证明：AAAA1⊥AA1CC；（2）求二面角BB−AA1CC−AA．16.（15分）已知定义在RR上的函数ff(xx)=aaxx4+bbxx3+ccxx2+ddxx(aa≠0)．（1）若原点是ff(xx)的一个极值点，证明：ff(xx)的所有零点也是其所有极值点；（2）若ff(xx)的4个零点成公差为2的等差数列，求ff′(xx)的最大零点与最小零点之差．17.（15分）设点SS(1,1)在椭圆CC:xx2aa2+yy2bb2=1(aa>bb>0)内，直线ll:bb2xx2+aa2yy2−aa2bb2=0 ．（1）求ll与CC的交点个数；（2）设PP为ll PPSS与CC相交于MM,NN两点．给出下列命题：①存在点PP，使得1|PPPP|,1|PPPP|,1|PPPP|成等差数列；②存在点PP，使得|PPMM|,|PPSS|,|PPNN|成等差数列；③存在点PP，使得|PPMM|,|PPSS|,|PPNN|成等比数列；请从以上三个命题中选择一个，证明该命题为假命题．（若选择多个命题分别作答，则按所做的第一个计分．）18.（17分）2024部分省市的高考数学推行8道单选，3道多选的新题型政策．单选题每题5分，选错不得分，多选题每题完全选对6分，部分选对部分分（此处直接视作3分），不选得0分．现有小李和小周参与一场新高考数学题，小李的试卷正常，而小周的试卷选择题是被打乱的，所以他11题均认为是单选题来做．假设两人选对一个单选题的概率都是14，且已知这四个多选题都只有两个正确答案．（1）记小周选择题最终得分为XX，求EE(XX)．（2）假设小李遇到三个多选题时，每个题他只能判断有一个选项是正确的，且小李也只会再选1个选项，假设他选对剩下1个选项的概率是 pp 0�pp 0≥13� ，请你帮小李制定回答4个多选题的策略，使得分最高．19.（17分）信息论之父香农（Shannon ）在1948年发表的论文“通信的数学理论”中指出，任何信息都存在冗余，冗余大小与信息中每个符号（数字、字母或单词）的出现概率或者说不确定性有关．香农借鉴了热力学的概念，把信息中排除了冗余后的平均信息量称为“信息熵”，并给出了计算信息熵的数学表达式．设随机变量 XX 所有取值为 1,2,…,nn ，且 PP (xx =ii )=PP ii >0（ii =1,2,…,nn ），PP 1+PP 2+⋯+PP nn =1 ，定义 XX 的信息熵HH (XX )=−�PP ii log 2PP ii nn ii=1（1）当 nn =1 时，求 HH (XX ) 的值；（2）当 nn =2 时，若 PP 1∈�0,12� ，探究 HH (XX ) 与 PP 1 的关系，并说明理由； （3）若 PP 1=PP 2=12nn−1 ，PP kk+1=2PP kk (kk =2,3,⋯,nn ) ，求此时的信息熵 HH (XX ) ．2024年新高考改革适应性练习（3）（九省联考题型）数学参考答案一、单项选择题（本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．）题号 1 2 3 4 5 6 7 8 答案 A B D A D D B C二、多项选择题（本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，有选错的得0分，若只有2个正确选项，每选对一个得3分；若只有3个正确选项，每选对一个得2分．具体得分如【附】评分表．）题号91011答案BC ABD BCD【附】评分表三、填空题（本题共3小题，每小题5分，共15分．）题号121314答案132023×2024+4×2024（或 2027×2024）3+3√10四、解答题（本题共5小题，共77分．解答应写出文字说明，证明过程或演算步骤．）15.（13分）以点AA1为坐标原点，AA1BB1���������⃗为xx轴正方向，AA1DD1����������⃗为yy轴正方向，AA1AA�������⃗为zz轴正方向，建立空间直角坐标系OOxxyyzz，并令正方体AABBAADD−AA1BB1AA1DD1的棱长为1．（1）则AA1(0,0,0)，AA(1,−1,1)，AA1AA�������⃗=(1,−1,1)；AA(0,0,1)，DD1(0,−1,0)，AADD1�������⃗=(0,−1,−1)．所以AADD1�������⃗·AA1AA�������⃗=0+1+(−1)=0 ，即AADD1�������⃗⊥AA1AA�������⃗．故AADD1⊥AA1AA得证．（2）BB(1,0,1)，AA1BB�������⃗=(1,0,1)，由（1）得AA1AA�������⃗=(1,−1,1)，设平面AA1BBAA的一个法向量nn11=(xx1,yy1,zz1)，则nn11·AA1BB�������⃗=nn11·AA1AA�������⃗=0 ，即�xx1+zz1=0xx1−yy1+zz1=0令xx1=1 ，则�yy1=0zz1=−1，所以nn11=(1,0,−1)是平面AA1BBAA的一个法向量．同理可求得平面AA1AADD的一个法向量nn22=(0,1,1)，cos<nn11,nn22>=nn11·nn22|nn11|·|nn22|=−12又 <nn11,nn22>∈(0,ππ)，所以 <nn11,nn22>=2ππ3，即平面AA1BBAA与平面AA1AADD的所成角为2ππ3．故二面角BB−AA1AA−DD的大小为2ππ3．16.（15分）（1）ff(xx)=aaxx4+bbxx3+ccxx2+ddxx，ff′(xx)=aaxx3+bbxx2+ccxx+dd，由题意，原点是ff(xx)的一个极值点，即ff′(0)=0 ，代入得dd=0 ，所以ff(xx)=aaxx4+bbxx3+ccxx2=xx2(aaxx2+bbxx+cc)，ff′(xx)=aaxx3+bbxx2+ccxx=xx(aaxx2+bbxx+cc)，所以ff(xx)和ff′(xx)的零点（0除外）都是方程aaxx2+bbxx+cc=0 的根，即ff(xx)和ff′(xx)有共同零点，故ff(xx)的所有零点也是其所有极值点．（2）设ff(xx)的四个零点分别为mm−3 ，mm−1 ，mm+1 ，mm+3 ，则可以设ff(xx)=kk(xx−mm+3)(xx−mm+1)(xx−mm−1)(xx−mm−3)其中kk≠0 ，令tt=xx−mm，则ff(xx)=kk(tt+3)(tt+1)(tt−1)(tt−3)=kk(tt4−10tt+9)=gg(tt)gg′(tt)=kk(4tt3−20tt)=4kk(tt3−5tt)令gg′(tt)=0 得tt1=−√5 ，tt=0 ，tt=√5 ，所以 ff ′(xx )=0 的所有根为 xx 1=mm −√5 ，xx 2=mm ，xx 3=mm +√5 ，所以 ff ′(xx ) 的最大零点与最小零点之差为 |xx 3−xx 1|=2√5 ．17.（15分）（1）因为点 SS (1,1) 在 AA 内，所以 1aa 2+1bb 2<1 ，即 aa 2+bb 2−aa 2bb 2<0 ． 联立 ll 与 AA 的方程，得 bb 2(aa 2+bb 2)xx 2−2aa 2bb 4xx +aa 4bb 2(bb 2−1)=0 ． 判别式 Δ=4aa 4bb 8−4aa 4bb 4(aa 2+bb 2)(bb 2−1)=4aa 4bb 4(aa 2+bb 2−aa 2bb 2)<0 ，故该二次方程无解，即 ll 与 AA 交点个数为0．（2）可选择命题②或命题③（命题①无法证伪），证明其为假命题． 记点 PP ,MM ,NN 的横坐标分别为 xx PP ,xx MM ,xx NN ，不妨设 PP ,MM ,SS ,NN 顺次排列．选择命题②的证明：当直线 MMNN 的斜率不存在时，MMNN :xx =1 ，分别与 ll ,AA 的方程联立可得 PP �1,bb 2−bb 2aa 2� ，MM �1,bb�1−1aa 2�,NN �1,−bb�1−1aa 2� ． 若 |PPMM |,|PPSS |,|PPNN | 依次成等差数列，则 bb�1−1aa 2+�−bb�1−1aa 2�=2 ，显然矛盾，不满足题意．当直线 MMNN 的斜率存在时，设其斜率为 kk ，则 MMNN :yy =kk (xx −1)+1 ，与 ll 的方程联立可得 xx PP =aa 2�bb 2+kk−1�aa 2kk+bb 2；与 AA 的方程联立，得 (aa 2kk 2+bb 2)xx 2−2aa 2kk (kk −1)xx +aa 2[(kk −1)2−bb 2]=0 ，由韦达定理⎩⎨⎧xx MM +xx NN =2aa 2kk (kk −1)aa 2kk 2+bb 2xx MM xx NN =aa 2[(kk −1)2−bb 2]aa 2kk 2+bb 2则 2|PPSS |−(|PPMM |+|PPNN |)=√1+kk 2(2|xx PP −1|−|xx MM −xx PP |−|xx NN −xx PP |) . 不妨设 xx PP >1 ，则 xx PP >xx MM >1>xx NN ， 所以原式=�1+kk 2[2(xx PP −1)−(xx PP −xx MM )−(xx PP −xx NN )]=�1+kk 2(xx MM +xx NN −2)=�1+kk 2⋅−2aa 2kk −2bb 2aa 2kk 2+bb 2<0因此 |PPMM |,|PPSS |,|PPNN | 不能成等差数列，从而②是假命题．选择命题③的证明：当直线 MMNN 的斜率不存在时，MMNN :xx =1 ，分别与 ll ,AA 的方程联立可得 PP �1,bb 2−bb 2aa 2� ，MM �1,bb�1−1aa 2�，NN �1,−bb�1−1aa 2�． 若|PPMM |,|PPSS |,|PPNN |成等比数列，则��bb 2−bb 2aa 2�−bb �1−1aa 2�×��bb 2−bb 2aa 2�+bb �1−1aa 2�=��bb 2−bb 2aa2�−1�2即 aa 2+aa 2bb 2−bb 2=0 ，但 aa 2bb 2>aa 2+bb 2 ，因此 aa 2+aa 2bb 2−bb 2>2aa 2>0 ，矛盾，不满足题意．当直线 MMNN 的斜率存在时，设其斜率为 kk ，则 MMNN :yy =kk (xx −1)+1 ，与 ll 的方程联立可得 xx PP =aa 2�bb 2+kk−1�aa 2kk+bb 2；与 AA 的方程联立，得 (aa 2kk 2+bb 2)xx 2−2aa 2kk (kk −1)xx +aa 2[(kk −1)2−bb 2]=0 ，由韦达定理，⎩⎨⎧xx MM +xx NN =2aa 2kk (kk −1)aa 2kk 2+bb 2xx MM xx NN =aa 2[(kk −1)2−bb 2]aa 2kk 2+bb 2则|PPSS |2−|PPMM |⋅|PPNN |=�1+kk 2[(xx PP −1)2−(xx PP −xx MM )(xx PP −xx NN )] =�1+kk 2[(xx MM +xx NN −2)xx PP +1−xx MM xx NN ]=�1+kk 2��2aa 2kk (kk −1)aa 2kk 2+bb 2−1�⋅aa 2(bb 2+kk −1)aa 2kk +bb 2+1−aa 2[(kk −1)2−bb 2]aa 2kk 2+bb 2�=√1+kk 2aa 2kk 2+bb 2(aa 2+bb 2−aa 2bb 2)<0 因此 |PPMM |,|PPSS |,|PPNN | 不能成等比数列，故③是假命题．18.（17分）（1）由题意，对于单选题，小周每个单选题做对的概率为 14 ， 对于多选题，小周每个多选题做对的概率为 12，设小周做对单选题的个数为 XX 1 ，做对多选题的个数为 XX 2 ， 则XX 1∼BB �8,1�，XX 2∼BB �3,1� ，所以EE(XX1)=8×14=2 ，EE(XX1)=3×12=32，而小周选择题最终得分为XX=5XX1+3XX2，所以EE(XX)=5EE(XX1)+3EE(XX2)=5×2+3×32=292．（2）由题意他能判断一个选项正确，先把这个正确选项选上，如果他不继续选其他选项肯定能得三分，如果他继续选其它选项的话，设此时他的最终得分为XX3，则XX3的所有可能取值为0，6，则XX3的分布列为：XX30 6PP(XX3)1−pp0pp0那么这个题的得分期望是EE(XX3)=0×(1−pp0)+6pp0=6pp0,�pp0≥13�所以我们只需要比较3和 6pp0的大小关系即可，令 6pp0≥3，解得12≤pp0<1 ，此时四个多选题全部选两个选项得分要高，反之，若13≤pp0<12，此时四个多选只选他确定的那个选项得分最高．19.（17分）（1）若nn=1 ，则ii=1 ，PP1=1 ，因此HH(xx)=−(1×log21)=0 ．（2）HH(XX)与PP1正相关，理由如下：当nn=2 时，PP1∈�0,12�，HH(xx)=−PP1log2PP1−(1−PP1)log2(1−PP1)令ff(tt)=−tt log2tt−(1−tt)log2(1−tt)，其中tt∈�0,12�，则ff′(tt)=−log2tt+log2(1−tt)=log2�1tt−1�>0所以函数ff(tt)在�0,12�上单调递增，所以HH(xx)与PP1正相关．（3）因为PP1=PP2=12nn−1，PP kk+1=2PP kk(kk=2,3,⋯,nn)，所以PP kk =PP 2⋅2kk−2=2kk−22nn−1=12nn−kk+1 (kk =2,3,⋯,nn ) 故PP kk log 2PP kk =12nn−kk+1log 212nn−kk+1=−nn −kk +12nn−kk+1而PP 1log 2PP 1=12nn−1log 212nn−1=−nn −12nn−1于是HH (XX )=nn −12nn−1+�PP kk log 2PP kk nnkk=2=nn −12nn−1+nn −12nn−1+nn −22nn−2+⋯+222+12整理得HH (XX )=nn −12nn−1−nn 2nn +nn 2nn +nn −12nn−1+nn −22nn−2+⋯+222+12 令SS nn =12+222+323+⋯+nn −12nn−1+nn2nn 则12SS nn =122+223+324+⋯+nn −12nn +nn 2nn+1 两式相减得12SS nn =12+122+123+⋯+12nn −nn 2nn+1=1−nn +22nn+1 因此 SS nn =2−nn+22nn， 所以 HH (XX )=nn−12nn−1−nn 2nn+SS nn =nn−12nn−1−nn 2nn+2−nn+22nn=2−12nn−2．。

1
万有文库
文体论
薛凤昌著
商务印书馆发行
第一页
上一页下一页最后一页
第一页上一页下一页最后一页
当前第2页/共48页
当前第2页/共48页
第一页上一页下一页最后一页
第一页上一页下一页最后一页48页
第一页上一页下一页最后一页
第一页上一页下一页最后一页48页
第一页上一页下一页最后一页
第一页上一页下一页最后一页48页
第一页上一页下一页最后一页
第一页上一页下一页最后一页48页
第一页上一页下一页最后一页
第一页上一页下一页最后一页48页
第一页上一页下一页最后一页
第一页上一页下一页最后一页48页
第一页上一页下一页最后一页
第一页上一页下一页最后一页48页
第一页上一页下一页最后一页
第一页上一页下一页最后一页48页。

机密★启用前2019年湖北省技能高考联考试卷农学类种植专业本试题卷共4页，55小题。

全卷满分150分，考试用时40分钟。

★祝考试顺利★注意事项：1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2．答题时，每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3．考试结束后，请将本试题卷和答题卡一并上交。

一、单项选择题（本大题共30小题，每小题3分，共90分）下列每小题给出的四个备选项中只有一项是符合题目要求的，请在答题卡上对应区域将正确答案代码涂黑。

错涂、多涂或未涂均无分。

1．在植物细胞中，合成蛋白质的细胞器是（）。

A．线粒体B．叶绿体C．核糖体D．液泡2．下列植物的维管束属于无限维管束的是（）。

A．小麦B．玉米C．水稻D．桃3．遗传物质DNA的中文名称为（）。

A．核苷酸B．脱氧核苷酸C．脱氧核糖核酸D．核糖核酸4．在有丝分裂中染色体排列在赤道面上的时期和染色体数目增加一倍的时期分别是（）。

A．前期、中期B．中期、后期C．后期、前期D．后期、末期5．下列植物及其花序对应不正确的是（）。

A．白菜——总状花序B．水稻——圆锥花序C．伞形花序——葱D．隐头花序——梨6．有利于提高根冠比的因素是（）。

A．增加土壤水分B．降低土壤水分C．较高温度D．氮肥过多7．维持植物正常生长所需的最低光照强度应为（）。

A．等于光补偿点B．大于光补偿点C．等于光饱和点D．大于光饱和点8．种子萌发时需要的养料是由（）提供的。

A．胚囊B．胚乳或子叶C．胚D．光合作用9．土壤中钾含量最高的是（）。

A．水溶性钾B．交换性钾C．缓效性钾D．矿物态钾10．水稻等禾本科植物的特有果实类型是（）。

A．蒴果B．角果C．颖果D．瓠果11．水分临界期是农作物各不同生育期中对水分缺乏（）的时期。

A．敏感B．比较敏感C．不敏感D．最敏感12．以9时为代表，土壤上层是日射型，下层是辐射型，称为（）。

2020-2021学年度第一学期期末质量检测五年级数学试题题号一二三四五六总分得分一、我会填。

（28分）1.在1~20各数中，质数有（）个，偶数有（）个。

2.167减去（）个它的分数单位等于1；811加上（）个它的分数单位等于最小的质数。

3.在直线上面填入真分数或假分数，在直线下面填入带分数。

4. 600cm2=（）dm2 300000m2=（）公顷5.在里填上“>”“<”或“=”。

16 5 32547583273.28 8公顷 8000平方米6.45=16（）=（）45=（）（填小数）7.），最小公倍数是（）。

8.两个因数的积是2.42，其中一个因数是22，另一个因数是( )。

9.把2米长的钢管平均分成5段，每段长( )米，每段是全长的（）（）。

10.一把钥匙可以开下列四把锁，这个钥匙上的数是（）。

11.盒子里放了5个红球和6个白球，任意摸出1个并放回去，摸若干次，摸到（）球的次数可能多，摸到（）球的次数可能少。

12.摆一个平行四边形需要4根小棒，摆两个平行四边形需要7根小棒，照这样摆下去，摆8个平行四边形需要（）根小棒，100根小棒可以摆（）个平行四边形。

13.体育馆内，14张乒乓球台上共有40人打球，正在进行单打的乒乓球台有（）张，双打的乒乓球台有（）张。

二、精挑细选。

（8分）1.下列各式中，与1.26÷0.28的商相等的是（）。

A.12.6÷2.8B.12.6÷0.28C.1.26÷2.8D.12.6÷282.下面图形是轴对称图形的是（）。

A. B. C. D.3.分子是8的假分数有（）个。

A.4B.7C.8D.无数4.甲数是乙数的倍数，甲乙两数的最大公因数是（）。

A.甲数B.乙数C.1D.甲乙两数的积5.下面的图形中，有（）个可由两个相同的梯形拼成。

A.1B.2C.3D.46.右图三个三角形面积的关系是（）。

A.①>②>③B.①=②=③C.①<②<③D.无法比较7.59的分子加15，要使分数的大小不变，分母应加（）。

A. A组中位数为2,极差为5
B.B组平均数为2,众数为2
C.C组平均数为1，方差大于0
D.D组平均数为2,方差为3
11.如图，矩形ABCD中，已知AB=2，BC=4，E为BC的中点.将AABE沿着Af：向上翻折至AMAE得
到四棱锥M—AECD，平面AEM与平面AECD所成锐二面角为《，直线ME与平面AECD所成角为/?，
(6+(i)
’
-a+6+c+(i.
21. (12 分）
已知函数 /(dzlrKx+D+mx2，m>0.
a)若/(x)在a，/a))处的切线斜率为求函数/〇r)的单调区间；
(2)g(x)=/(:c)—siar，若x=0是g(:c)的极大值点，求m的取值范围.
22. (12 分）
已知椭圆f：:^+¥ = l(a>K>〇)，巧、F2分别是椭圆的左、右焦点，_?是椭圆上的动点，直线PR交椭 a〇
:< !
#
%
&
'
(
"
)
* !$ !! !#
%& +
,
-
,
-
+
-
+ ,-+ .+ .,+ .-+
!!%&+ =>?@A#"$##B#$"B%&C $!
#!%&,
=>D%$#EFD& GHIJKE+L'/0&!(GHIM#1&!(/!)"=B(/#! %!%&-
有一门课程相同的概率为