人工地震波生成程序简介

引言：随着社会的快速发展，核电站和海洋平台迅速兴建，大型水坝、高层建筑和大跨桥梁日益增加，其中很多兴建于强震活动区。

由于这些结构物的重要性，加之缺乏这类工程及相应场地的抗震经验，对其抗震性能的研究引起了社会和工程界的重视。

并且相应的抗震规范都规定，在上述重要结构的设计中，应当采用地震动时程输入结构动力分析来考虑地震动时间过程影响。

由于很难在天然地震中取得相应场的地峰值和反应谱，为探讨结构物在地震动反应中的耗能特性和破坏机理，必须对结构物在地震动作用下的整个过程进行模拟，用人工合成地震动方法，分析结构物及相应场地在地震动中的反应，因此对比天然地震动与人工合成地震动在相应场地反应的异同成为抗震设防的重点。

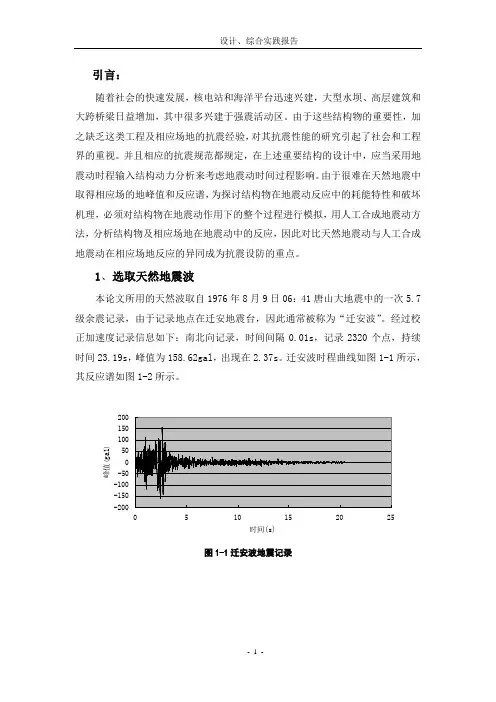
1、选取天然地震波本论文所用的天然波取自1976年8月9日06：41唐山大地震中的一次5.7级余震记录，由于记录地点在迁安地震台，因此通常被称为“迁安波”。

经过校正加速度记录信息如下：南北向记录，时间间隔0.01s，记录2320个点，持续时间23.19s，峰值为158.62gal，出现在2.37s。

迁安波时程曲线如图1-1所示，其反应谱如图1-2所示。

图1-1迁安波地震记录图1-2迁安波地震反应谱2、人工合成地震动在工程地震学研究中，采用多种方法来估计地震动。

其中包括基于幅值和卓越周期调整的比例方法、拟合目标峰值和反应谱的数值方法、选择实际地震动记录的地震记录匹配法及半经验半理论模拟方法。

下面我们采用拟合目标峰值和反应谱的数值方法，进行人工合成地震动。

随着强震动观测的发展及对地震宏观震害经验和仪器测量结果的大量分析研究发现，运用数值方法程序计算出的反应谱和加速度时程，可以通过地震动的工程特性三要素来描述即：地震动的振幅、频率和持续时间。

因此我们通过控制这三要素，运用Saw软件，更改随机数200，得到图2-1和图2-2如下：图2-1人工合成地震动时图2-2人工合成地震动反应谱3、 构建场地模型《建筑抗震设计规范》（GB50011－2001）规定采用剪切波速和覆盖层厚度两个物理性指标来进行确定场地类别。

地震工程学作业课程名称:地震工程学______ 指导老师:_______翟永梅_________ 姓名:史先飞________ 学号:1232627________一、地震波生成反应谱1 所取的地震波为Elcentro地震波加速度曲线，如图1所示。

图1 Elcentro地震波加速度曲线2 所调用的Matlab程序为：% ***********读入地震记录***********ElCentro;Accelerate= ElCentro(:,1)*9.8067;%单位统一为m和sN=length(Accelerate);%N 读入的记录的量time=0:0.005:(N-1)*0.005; %单位 s%初始化各储存向量Displace=zeros(1,N); %相对位移Velocity=zeros(1,N); %相对速度AbsAcce=zeros(1,N); %绝对加速度% ***********A,B矩阵***********Damp=0.02; %阻尼比0.02TA=0.0:0.05:6; %TA=0.000001:0.02:6; %结构周期Dt=0.005; %地震记录的步长%记录计算得到的反应，MaxD为某阻尼时最大相对位移，MaxV为某阻尼最大相对速度，MaxA某阻尼时最大绝对加速度，用于画图MaxD=zeros(3,length(TA));MaxV=zeros(3,length(TA));MaxA=zeros(3,length(TA));t=1;for T=0.0:0.05:6NatualFrequency=2*pi/T ; %结构自振频率DampFrequency=NatualFrequency*sqrt(1-Damp*Damp); %计算公式化简e_t=exp(-Damp*NatualFrequency*Dt);s=sin(DampFrequency*Dt);c=cos(DampFrequency*Dt);A=zeros(2,2);A(1,1)=e_t*(s*Damp/sqrt(1-Damp*Damp)+c);A(1,2)=e_t*s/DampFrequency;A(2,1)=-NatualFrequency*e_t*s/sqrt(1-Damp*Damp);A(2,2)=e_t*(-s*Damp/sqrt(1-Damp*Damp)+c);d_f=(2*Damp^2-1)/(NatualFrequency^2*Dt);d_3t=Damp/(NatualFrequency^3*Dt);B=zeros(2,2);B(1,1)=e_t*((d_f+Damp/NatualFrequency)*s/DampFrequency+(2*d_3t+1/NatualFrequency^2)*c)-2*d_3 t;B(1,2)=-e_t*(d_f*s/DampFrequency+2*d_3t*c)-1/NatualFrequency^2+2*d_3t;B(2,1)=e_t*((d_f+Damp/NatualFrequency)*(c-Damp/sqrt(1-Damp^2)*s)-(2*d_3t+1/NatualFrequency^2 )*(DampFrequency*s+Damp*NatualFrequency*c))+1/(NatualFrequency^2*Dt);B(2,2)=e_t*(1/(NatualFrequency^2*Dt)*c+s*Damp/(NatualFrequency*DampFrequency*Dt))-1/(NatualF requency^2*Dt);for i=1:(N-1) %根据地震记录,计算不同的反应Displace(i+1)=A(1,1)*Displace(i)+A(1,2)*Velocity(i)+B(1,1)*Accelerate(i)+B(1,2)*Accelerate(i +1);Velocity(i+1)=A(2,1)*Displace(i)+A(2,2)*Velocity(i)+B(2,1)*Accelerate(i)+B(2,2)*Accelerate(i +1);AbsAcce(i+1)=-2*Damp*NatualFrequency*Velocity(i+1)-NatualFrequency^2*Displace(i+1);endMaxD(1,t)=max(abs(Displace));MaxV(1,t)=max(abs(Velocity));if T==0.0MaxA(1,t)=max(abs(Accelerate));elseMaxA(1,t)=max(abs(AbsAcce));endDisplace=zeros(1,N);%初始化各储存向量，避免下次不同周期计算时引用到前一个周期的结果Velocity=zeros(1,N);AbsAcce=zeros(1,N);t=t+1;End% ***********PLOT***********close allfigure %绘制地震记录图plot(time(:),Accelerate(:))title('PEER STRONG MOTION DATABASE RECORD')xlabel('time(s)')ylabel('acceleration(g)')gridfigure %绘制位移反应谱plot(TA,MaxD(1,:),'-.b',TA,MaxD(2,:),'-r',TA,MaxD(3,:),':k')title('Displacement')xlabel('Tn(s)')ylabel('Displacement(m)')legend('ζ=0.02')Gridfigure %绘制速度反应谱plot(TA,MaxV(1,:),'-.b',TA,MaxV(2,:),'-r',TA,MaxV(3,:),':k') title('Velocity')xlabel('Tn(s)')ylabel('velocity(m/s)')legend('ζ=0.02')Gridfigure %绘制绝对加速度反应谱plot(TA,MaxA(1,:),'-.b',TA,MaxA(2,:),'-r',TA,MaxA(3,:),':k') title('Absolute Acceleration')xlabel('Tn(s)')ylabel('absolute acceleration(m/s^2)')legend('ζ=0.02')Grid3 运行的结果得到的反应谱图2 位移反应谱图3 速度反应谱图4 加速度反应谱一、反应谱生成地震波1所取的反应谱为上海市设计反应谱图5 上海市设计反应谱2反应谱取值程序为：%%规范反应谱取值程序参照01年抗震规范function rs_z=r_s_1(pl,zn,ld,cd,fz) %%%pl 圆频率,zn阻尼比,ld烈度,cd场地类型,场地分组fz %%%%烈度选择if ld==6arfmax=0.11;endif ld==7arfmax=0.23;endif ld==8arfmax=0.45;endif ld==9arfmax=0.90;end%%%%场地类别，设计地震分组选择if cd==1if fz==1Tg=0.25;endif fz==2Tg=0.30;endif fz==3Tg=0.35;endendif cd==2if fz==1Tg=0.35;if fz==2Tg=0.40;endif fz==3Tg=0.45;endendif cd==3if fz==1Tg=0.45;endif fz==2Tg=0.55;endif fz==3Tg=0.65;endendif cd==4if fz==1Tg=0.65;endif fz==2Tg=0.75;endif fz==3Tg=0.90;endend%%%%%%%%%ceita=zn; %%%%%阻尼比lmt1=0.02+(0.05-ceita)/8;if lmt1<0lmt1=0;endlmt2=1+(0.05-ceita)/(0.06+1.7*ceita); if lmt2<0.55lmt2=0.55;endsjzs=0.9+(0.05-ceita)/(0.5+5*ceita); %%%%%分段位置 T1 T2 T3T1=0.1;T2=Tg;T_jg=2*pi./pl;%%%% 第一段 0～T1if T_jg<=T1arf_jg=0.45*arfmax+(lmt2*arfmax-0.45*arfmax)/0.1*T_jg;end%%%% 第二段 T1～T2if T1<T_jg&T_jg<=T2arf_jg=lmt2*arfmax;end%%%% 第三段 T2~T3if T2<T_jg&T_jg<=T3arf_jg=((Tg/T_jg)^sjzs)*lmt2*arfmax;end%%%% 第四段 T3～6.0if T3<T_jg&T_jg<=6.0arf_jg=(lmt2*0.2^sjzs-lmt1*(T_jg-5*Tg))*arfmax;end%%%% 第五段 6.0～if 6.0<T_jgarf_jg=(lmt2*0.2^sjzs-lmt1*(6.0-5*Tg))*arfmax;end%%%%%%反应谱值拟加速度值rs_z=arf_jg*9.8;end3生成人造地震波主程序：%%%主程序%%%%%%%%确定需要控制的反应谱Sa（T）(T=T1,...,TM)的坐标点数M，反应谱控制容差rc Tyz=[0.04:0.016:0.1,0.15:0.05:3.0,3.2:0.05:5.0];rc=0.06;nTyz=length(Tyz);ceita=0.035;%%%阻尼比：0.035for i=1:nTyzSyz(i)=r_s_1(2*pi/Tyz(i),ceita,8,2,1); %%%%8度，2类场地，第1地震分组end%%%%%% 变换的频率差：2*pi*0.005(可以保证长周期项5s附近有5项三角级数)；%%%%频率变化范围 N1=30, 30*0.005*2*pi ;N2=3000, 5000*0.005*2*piplc=2*pi*0.005;pl=30*0.005*2*pi:0.005*2*pi:10000*0.005*2*pi;npl=length(pl);P=0.9; %%%保证率%%%%%%人造地震动持续时间40s，时间间隔：0.02sTd=40;dt=0.02;t=0:0.02:40;nt=length(t);%%%%%%% 衰减包络函数t1=8; %%%%上升段t2=8+24; %%%%%平稳段; 下降段则为40－32＝8sc=0.6; %%%%衰减段参数for i=1:ntif t(i)<=t1f(i)=(t(i)/t1)^2;endif t(i)>t1 & t(i)<t2f(i)=1;endif t(i)>=t2f(i)=exp(-c*(t(i)-t2));endend%%%%%%% 反应谱转换功率谱for i=1:nplSw(i)=(2*ceita/(pi*pl(i)))*r_s_1(pl(i),ceita,8,2,1)^2/(-2*log(-1*pi*log(P)/(pl(i)*Td))); Aw(i)=sqrt(4*Sw(i)*plc);end%%%%%%%%%%%%%% 合成地震动at=zeros(nt,1);atj=zeros(nt,1);for i=1:nplfai(i)=rand(1)*2*pi;for j=1:ntatj(j)=f(j)*Aw(i)*real(exp(sqrt(-1)*(pl(i)*t(j)+fai(i))));endat=at+atj;end%%%%%%% 计算反应谱验证是否满足rc在5%的要求,需要时程动力分析%%%%%%%%%%%% response spectra of callidar%%%%%%% parameterg=9.8;m=1;x0=0;v0=0;ww=2*pi./Tyz;%%%%%%%% loadag=at; %%%%%%%修改%%%%%%% solutionfor y=1:nTyzz=0.037;w=ww(y);c=2*z*w;k=w^2;for i=1:nt-1p(i)=-ag(i+1)+ag(i);a0=m\(-ag(i)-c*v0-k*x0);kk=k+(dt^2)\(6*m)+dt\(3*c);pp=p(i)+m*(dt\(6*v0)+3*a0)+c*(3*v0+2\(dt*a0)); dx=kk\pp;dv=dt\(3*dx)-3*v0-2\(dt*a0);x1=x0+dx;x0=x1;v1=v0+dv;v0=v1;as(i)=a0;as(i)=as(i)+ag(i);vs(i)=v0;xs(i)=x0;endmaxas(y)=max(as);maxvs(y)=max(vs);maxxs(y)=max(xs);endfor i=1:nTyzrspa(i)=maxas(i);end%%%%%%% 比较容差for i=1:nTyzrcrsp(i)=abs(rspa(i)-Syz(i))/max(Syz(:));endjsnum=1;while max(rcrsp(:))>rc%%%%%循环体函数blxs=Syz./rspa;for xsxs=1:nplif 2*pi/pl(xsxs)<Tyz(1)blxs1(xsxs)=blxs(1);endfor sxsx=1:nTyz-1if (2*pi/pl(xsxs)>=Tyz(sxsx)) & (2*pi/pl(xsxs)<=Tyz(sxsx+1))blxs1(xsxs)=blxs(sxsx)+(blxs(sxsx+1)-blxs(sxsx))*(2*pi/pl(xsxs)-Tyz(sxsx))/(Tyz(sxsx+1)-Tyz(sxsx));endendif 2*pi/pl(xsxs)>Tyz(nTyz)blxs1(xsxs)=blxs(nTyz);endendAw=Aw.*blxs1;%%%%%%%%%%%%%% 合成地震动at=zeros(nt,1);atj=zeros(nt,1);for i=1:nplfor j=1:ntatj(j)=f(j)*Aw(i)*real(exp(sqrt(-1)*(pl(i)*t(j)+fai(i))));endat=at+atj;end%%%%%%% 计算反应谱验证是否满足rc在5%的要求%%%%%%%%%%%% response spectra of callidar%%%%%%% parameterg=9.8;m=1;x0=0;v0=0;ww=2*pi./Tyz;%%%%%%%% loadag=at; %%%%%%%修改%%%%%%% solutionfor y=1:nTyzz=0.037;w=ww(y);c=2*z*w;k=w^2;for i=1:nt-1p(i)=-ag(i+1)+ag(i);a0=m\(-ag(i)-c*v0-k*x0);kk=k+(dt^2)\(6*m)+dt\(3*c);pp=p(i)+m*(dt\(6*v0)+3*a0)+c*(3*v0+2\(dt*a0)); dx=kk\pp;dv=dt\(3*dx)-3*v0-2\(dt*a0);x1=x0+dx;x0=x1;v1=v0+dv;v0=v1;as(i)=a0;as(i)=as(i)+ag(i);vs(i)=v0;xs(i)=x0;endmaxas(y)=max(as);maxvs(y)=max(vs);maxxs(y)=max(xs);endfor i=1:nTyzrspa(i)=maxas(i);end%%%%%%% 比较容差for i=1:nTyzrcrsp(i)=abs(rspa(i)-Syz(i))/max(Syz(:));endjsnum=jsnum+1max(rcrsp(:))end%%%%%%% 最终的反应谱与规范谱%%%%%%%%%%%% response spectra of callidar%%%%%%% parameter%% Tjs=0.05:0.01:6;%% nTjs=length(Tjs);g=9.8;m=1;x0=0;v0=0;ww=2*pi./Tyz;%%%%%%%% loadag=at; %%%%%%%修改%%%%%%% solutionfor y=1:nTyzz=0.037;w=ww(y);c=2*z*w;k=w^2;for i=1:nt-1p(i)=-ag(i+1)+ag(i);a0=m\(-ag(i)-c*v0-k*x0);kk=k+(dt^2)\(6*m)+dt\(3*c);pp=p(i)+m*(dt\(6*v0)+3*a0)+c*(3*v0+2\(dt*a0));dx=kk\pp;dv=dt\(3*dx)-3*v0-2\(dt*a0);x1=x0+dx;x0=x1;v1=v0+dv;v0=v1;as(i)=a0;as(i)=as(i)+ag(i);vs(i)=v0;xs(i)=x0;endmaxas(y)=max(as);maxvs(y)=max(vs);maxxs(y)=max(xs);endfor i=1:nTyzrspa(i)=maxas(i)/g;rspa_S(i)=r_s_1(2*pi/Tyz(i),ceita,8,2,1)/g;endsubplot(2,1,1);plot(t,at);subplot(2,1,2);plot(Tyz,rspa);hold on;plot(Tyz,rspa_S);4生成的人造地震波如图所示。

怎么用Midas生成地震波?中的时程荷载函数。

MIDAS/GEN提供了32个地震加速度记录，这些都是原始的地震波数据。

如果需要人为处理，可以输入放大系数，或者是输入加速度最大值。

选取地震波时，需要根据规范规定，得到抗震设防烈度索对应的加速度时程曲线的最大值，再根据此值进行地震波的选择。

在MIDAS程序中，可选取两组实际强震记录生成两个SGS文件(调整Sa后的)，然后将一组人工模拟的加速度时程曲线也保存为SGS文件，将三个SGS文件的数值取平均后与振型分解反应谱法所采用的地震影响系数曲线相比较看是否满足在统计意义上相符，由此也可判断选取的地震波是否合适。

另外，弹性时程分析时，每条时程曲线计算所得到的结构底部剪力不应小于振型分解反应谱法计算结果的65%，多条时程曲线计算所得结构底部剪力的平均值不应小于振型分解反应谱法计算结果的80%。

当你针对不同的设防烈度或者是中震、大震的分析计算时，是需要自己调整原始地震波的峰值，以适应你所需要的分析。

比如是7度设防和8度设防，当采用时程分析时，那么所用的地震波的峰值肯定是不一样的，那么你这个时候就需要调整了。

在MIDAS程序中提供将地震波转换为绝对加速度反应谱和拟速度反应谱的功能(工具地震波数据生成器，生成后保存为SGS文件)，用户可利用保存的SGS文件(文本格式文件)根据上面所述方法计算Sv、Sa、Tg。

通过Tg值可判断该地震波是否适合当地场地和地震设计分组，然后将抗震规范中表5.1.2-2中的EPA值与Sa相比求出调整系数，将其代入到地震波调整系数中。

将地震波转换为绝对加速度反应谱和拟速度反应谱时注意周期范围要到6秒(建筑抗震规范规定)。

建筑抗震设计规范5.1.2条中规定，采用时程分析方法时，应按照场地类别和设计地震分组选用不少于二组的实际强震记录和一组人工模拟的加速度时程曲线，其平均地震影响系数曲线应与振型分解反应谱法所采用的地震影响系数曲线在统计意义上相符。

拟合水工设计反应谱的人工地震波的生成与H uang 变换校正姚艳华彭刚陈灯红摘要:根据非平稳输入下建立的功率谱与均值反应谱之间的关系,合成基于水工设计反应谱的人工地震波,并对其幅值进行修正,降低了高频区误差作用;为了解决加速度时程积分后的速度、位移时程的零线漂移现象,利用H ua ng 变换得到加速度时程的固有模态函数,由H ua ng 变换方法得到的最低频率固有模态函数分量通常情况下代表原始信号的趋势或均值,对去掉均值后的加速度时程进行积分得到的速度、位移时程不存在零线漂移问题。

关键词:人工地震波; 功率谱; 幅值谱; H u a n g 变换; 固有模态函数The Synt hesis an d Huang T ransf orm Correct i on of Si mulatedE art hqua ke Wave on Hydra u l i c Design R esponse SpectrumYao Ya n hua Pe ng Ga ng C he n De ngho ngAbstract A met h o d t h at ca n si m ulat e ea r t h qua k e wa v e ba s e o n hydra u lic de s i g n re s po n s e sp ect r u m a nd t he relatio n ship of po we r sp ect r um a nd mea n re spo n se sp ect r um i n t h e no n2 st atio n i np ut i s p re se nt e d. It ca n be u se d to mo dif y t he i nit ial wa ve a nd reduce t he er r o r of hi gh f reque ncy . In o r der to sol ve t he shif t of velocit y a nd di sp lace me nt o bt ai ne d by i n t e g ra2 ti ng acceleratio n , t he H ua ng t ra n s fo r m i s u se d to o bt ai n t h e i nt ri n sic m o de f u ncti o n s of ac2 cele r atio n.The lo w e s t f reque n cy i n t r i n s ic mo d e f u n ctio n i s ge n e r all y t h e mea n val u e o r t r e n d of si g nal s. The velocit y a n d di s p l ace m e n t o b t a i n ed by i n t e grati n g t h e acceleratio n w h ich i s deduct e d t r e n d do n’t have t h e s hif t p r o b le m.K ey w ords si m ulat e d ea r t h qua k e wa v e ; po w e r sp e ct r u m ; a m p lit u de sp e ct r u m ;H u a n g t r a n s fo r m ; i n t ri n s ic mo d e f u nctio n s基金项目: 国家自然科学基金重大研究计划重点项目( 90510017) ;中国博士后科学基金资助( 20060390832)作者简介: 姚艳华( 1984 - ),女,三峡大学土木水电学院硕士研究生;邮编:443002 。

人工地震波依据三角级数法武汉@桥梁隧道 799084759采用shinozuka 的方法来模拟平稳化后的随机地面运动加速度()()()..g x t f t t ς=⨯其中： ()1()cos nk k k k f t C t ωϕ==+∑k C =()()()21ln ln 1T k a S S P T ξωωππωω⎡⎤=⎣⎦-⎡⎤-⎢⎥⎣⎦强度包线：()()()()()2000/1exp n n n t t t t t t t t t t c t t t t ς 0ςς⎧=≤≤⎪⎪= ≤≤⎨⎪=-- ≤⎡⎤⎪⎣⎦⎩P ——反应超越概率。

S ——功率谱密度函数。

∆ω——频谱分度（rad/s ）。

S a T （ω）——给定的目标加速度反应谱。

φk ——均匀分布在0~2π之间的随机数。

具体matlab 程序如下：%形成人工波主程序w=[0.04:0.02:0.1,0.15:0.05:3.0,3.2:0.1:5.0]';%频谱范围 wn=length(w);TT=30;%持时dltw=2*pi/TT;%Δwag=zeros(30/0.02+1,1);sw=0;kist=0;for n=0:30/0.02ckn=0;for i=1:wnck=sqrt(4*sw1(w(i))*dltw);ckn=ck*cos(w(i)*n*0.02+rand(1)*2*pi)+ckn; endag1(n+1)=ckn;ag2(n+1)=ft(n*0.02);ag(n+1)=ft(n*0.02)*ckn;endt=0:0.02:30;subplot(221)plot(t,ag)title('地震波')xlabel('t=0:30 (s)')ylabel('ag (m/s2)')subplot(222)plot(t,ag1)title('功率谱密度函数（随机后）')xlabel('t=0:30 (s)')ylabel('∑Ck*cos() (m/s2)')subplot(223)plot(t,ag2)title('强度包线')xlabel('t=0:30 (s)')ylabel('ξ (m/s2)')%强度包线子程序function ksit=ft(t)t0=2;tn=10;c=0.2;if t>=0&&t<=t0ksit=(t/t0)^2;elseif t>t0&&t<tnksit=1;elseksit=exp(-c*(t-tn));endend%计算功率密度函数子程序function sw=sw1(w)T=2*pi/w;ksi=0.05;r=0.9+(0.05-ksi)/(0.5+5*ksi);eit1=0.02+(0.05-ksi)/8;eit2=1+(0.05-ksi)/(0.06+1.7*ksi);Tg=0.4;%第二类场地第二组amax=0.8;%七度区多遇地震if(T>0&&T<0.1)st=0.45*amax/eit2+(amax-0.45*amax/eit2)/0.1; elseif T>0.1&&T<Tgst=amax;elseif T>Tg&&T<5*Tgst=(Tg/T)^r*amax;elsest=(0.2^r-eit1/eit2*(T-5*Tg))*amax;endp=0.9;%P为反应超越概率，一般取0.85<P<1 sw=ksi/(pi*w)*st^2/log(-pi/(w*T)*log(1-p)); end。

clearclcclose all hidden %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%fni=input('生成人工地震波-输入数据文件名(20041012):','s');fid=fopen(fni,'r');fs=fscanf(fid,'%f',1);%采样频率tu=fscanf(fid,'%f',1);%上升时间长度%上升时间包络线线形(1-直线、2-抛物线、3-指数曲线)iu=fscanf(fid,'%f',1);%上升时间包络线线形参数（只有指数曲线需要具体参数，其均为1）cu=fscanf(fid,'%f',1);ta=fscanf(fid,'%f',1);%持时时间长度td=fscanf(fid,'%f',1);%下降时间长度%下降时间包络线线形(1-直线、2-抛物线、3-指数曲线)id= fscanf(fid,'%f',1);%下降时间包络线线形（只有抛物线，指数曲线需要具体参数，其余为1）cd=fscanf(fid,'%f',1);dp=fscanf(fid,'%f',1);%阴尼比值p=fscanf(fid,'%f',1);%概率系数（一般可取P=0.85）nn=fscanf(fid,'%f',1);%迭代次数fno=fscanf(fid,'%f',1);%输出数据文件名%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %对目标反应谱取值x=fscanf(fid,'%f',[2,inf]);%反应谱频率和幅值数据%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% tatus=fclose(fid);%计算生成地震波的数据长度tl=tu+ta+td;%计算生成地震波的数据长度nt=round(fs*tl+1);%大于并最接近nt的2的幂次方为FFT长度nfft=2^nestpow2(nt)%计算频率间隔（Hz）df=fs/nfft%定义反应谱的离散频率向量f=0:df:(nfft/2-1)*df%计算时间间隔（s）dt=1/fs;%定义的离散时间向量t=0:dt:(nt-1)*dt%生成0到2PI的随机数为随机相位g=rand(1,nfft/s)*2*pi;%建立时间包络线%建立与地震波长度相同元素为1的向量en=ones(1,nt);%上升时间阶段%确定上升时间段的长度l=round(tu*fs)+1%产生上升时间段的包络线数组元素switch iucase 1 %直线en(1:l)=linspace(0,1,1);% y = linspace(a,b,n) generates a row vector y of n points linearlyspaced between and including a and b.case 2 %抛物线a=0:l-1;en(1:l)=(a/(l-1)).^2;case 3 %指数曲线a=0:l-1;en(1:l)=1-exp(-cu*a/(l-1));end%持续时间阶段%确定0时刻到持续时间结束时刻时间段的长度m=round((tu+ta)*fs)+1;%下降时间阶段%产生下降时间段的包络线数组元素switch idcase 1 %直线en(m:nt)=linspace(1,0,nt-m+1);case 2 %抛物线a=0:nt-m;en(m:nt)=1-cd*(a/(nt-m)).^2;case 3 %指数曲线a=0:nt-m;en(m:nt)=exp(-cd*a/(nt-m));end%按线性插值建立目标反应谱离散数据%按目标反应谱的长度生成元素为0的向量a0=zeros(x(1,:));%取目标反应谱数据的长度n=length(x(1,:));%四舍五入取整求反应谱最大频率对应数组元素的下标nb=round(x(1,n)/df)+1;for k=1:n-1%四舍五入取整求反应谱前一个频率数据对应数组元素的下标 l=round(x(1,K)/df)+1;%四舍五入取整求反应谱后一个频率数据对应数组元素的下标m=round(x(1,K+1)/df)+1;%线性插值产生前后两个频率数据间的反应谱数组元素 a0(1:m)=linspace(x(2,k),x(2,k+1),m-l+1)end%根据目标反应谱计算对应的近似功率谱a1=a0;s=zeros(1,nfft/2);k=nb:ne;s(k)=2*dp/(pi.*(a1(k).^2)./f(k)./(-2*log(-log(p)*pi/tl)./f(k)));%将功率谱转换成傅里叶幅值谱b1=sqrt(4*df*s)*nfft/2;%定义元素为0的反谱传递函数矩阵hf=zeros(ne,nfft);%计算加速度反应谱传递函数矩阵for j-0:ne-1w=2*pi*df*jwd=w*sqrt(1-dp*dp);e=exp(-t.*W*dp);a=t.*wd;s=sin(a)>*((1-2*dp*dp)/(1-dp*dp));c=cos(a).*(2*dp/sqrt(1-dp*dp));%计算加速度反应谱的脉冲响应函数向量h=wd*e.*(s+c)/fs;%通过FFT变换求加速度反应谱传递函数向量hf(j+1,:)=fft(h,nfft);endmm=nn%进行生成人工地震波迭代计算%100为最大迭代次数for k=1:100%将幅值谱和相位谱转化为实部和虚部c=b1.*exp(i*g);%将正负圆频率傅里叶谱向量组合成一仙向量d=[c,c(nfft/2:-1:1)];%IFFT变换，并取变换结果实部为生成的地震波e=ifft(d,nfft);%给生成的地震波加上强度包络线y=en.*real(e(1:nt));%计算反应谱%对生成的地震波进行FFT变换yf=fft(y,nfft);for j=1:ne%用地震波FFT变换结果和反应谱传递函数的乘积的逆变换做卷积运算 d=ifft(yf.*hf(j,:),nfft);%求各频率对应地震的最大响应al(j)=max(real(d(1:nt)));end%如果达到指定的迭代次数显于图形if k==mmsubplot(2,1,1);%m 同时显示生成的地震波的强度包络线plot(t,y,t,en,t,-en);xlabel('时间（s）');ylabel('加速度（g）');grid onsublpot(2,1,2);%同时显示期望反应谱与反应谱计算谱、l=1:neplot(f(l),a0(l),':'f(l),a1(l));xlabel('频率（Hz）');ylabel('加速度（g）');legend('目标谱','计算谱');grid on;ig=input('继续迭代次数[取值1-9,否则退出]:');if ig>0&ig<10 %如果输入数字是1-9mm=mm+igelsebreak;endendc=bl%期望谱与计算谱的比值来修改傅里叶值谱j=nb:ne;bl(j)=c(j).*a0(j)./a1(j);end%打开文件输入人工地震动数据fid=fopen(fno,'W');for K=1:nt%每一行输出两个实型数据,t为时间,y为人工地震动信号值 fprintf(fid,'%f%f\n',t(k),y(k));endstatus=fclose(fid);。

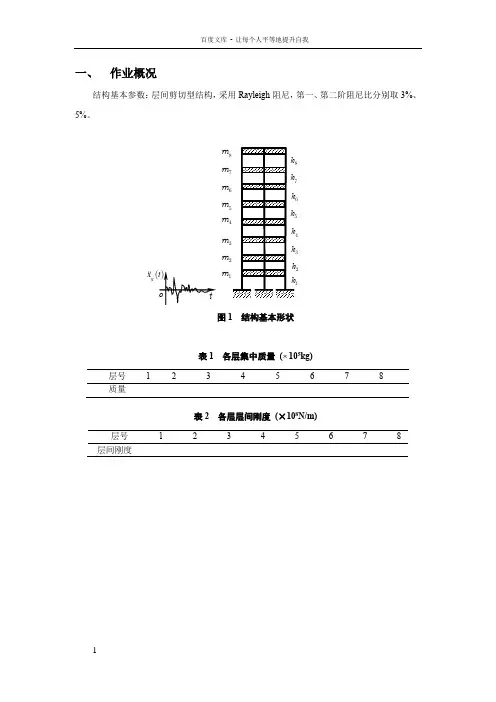
一、 作业概况结构基本参数：层间剪切型结构，采用Rayleigh 阻尼，第一、第二阶阻尼比分别取3%、5%。

图1 结构基本形状表1 各层集中质量 ( 105kg)层号 12345678质量表2 各层层间刚度 (×108N/m)层号 1 2 3 4 5 6 7 8 层间刚度m m m m m m m m ()g x t二、 频率及振型计算根据层间模型的假定，可以建立结构的质量矩阵以及刚度矩阵如下。

12345678000000000000000000000000000000000000000000000000000000003.400000000 3.400000000 3.200000000 3.20000 =0000 2.800000000 2.800000000 2.700000000 2.6m m m m m m m m ⎛⎫ ⎪ ⎪ ⎪ ⎪⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎛⎫ ⎝M 510kg ⎪⎪⎪⎪⎪⨯⎪⎪⎪⎪⎪⎪⎭ 11121314151617182122232425262728313233343536373841424344454647485152535455565758616263646566676871727374757677788182838485868788k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k ⎛ =⎝K 8420000002 3.8 1.8000000 1.8 3.6 1.8000000 1.8 3.6 1.8000 =10/000 1.8 3.6 1.8000000 1.8 3.4 1.6000000 1.6 3.2 1.6000000 1.6 1.6N m ⎫⎪⎪⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎭-⎛⎫ ⎪-- ⎪ ⎪-- ⎪-- ⎪⨯ ⎪-- ⎪-- ⎪ ⎪-- ⎪ ⎪-⎝⎭根据上面求得的质量、刚度矩阵，即可求解特征方程：20K M（1）求解自振频率以及阵型向量已经演变成为典型的求解矩阵特征值以及特征向量的问题，特征值即为圆频率2，特征向量即为振型向量。

地震工程学作业课程名称:地震工程学______指导老师:_______翟永梅_________姓名:史先飞________学号: 1232627________一、地震波生成反应谱1 所取的地震波为Elcentro地震波加速度曲线，如图1所示。

图1 Elcentro地震波加速度曲线2 所调用的Matlab程序为：% ***********读入地震记录***********ElCentro;Accelerate= ElCentro(:,1)*;%单位统一为m和sN=length(Accelerate);%N 读入的记录的量time=0::(N-1)*; %单位 s%初始化各储存向量Displace=zeros(1,N); %相对位移Velocity=zeros(1,N); %相对速度AbsAcce=zeros(1,N); %绝对加速度% ***********A,B矩阵***********Damp=; %阻尼比TA=::6; %TA=::6; %结构周期Dt=; %地震记录的步长%记录计算得到的反应，MaxD为某阻尼时最大相对位移，MaxV为某阻尼最大相对速度，MaxA某阻尼时最大绝对加速度，用于画图MaxD=zeros(3,length(TA));MaxV=zeros(3,length(TA));MaxA=zeros(3,length(TA));t=1;for T=::6NatualFrequency=2*pi/T ; %结构自振频率DampFrequency=NatualFrequency*sqrt(1-Damp*Damp); %计算公式化简e_t=exp(-Damp*NatualFrequency*Dt);s=sin(DampFrequency*Dt);c=cos(DampFrequency*Dt);A=zeros(2,2);A(1,1)=e_t*(s*Damp/sqrt(1-Damp*Damp)+c);A(1,2)=e_t*s/DampFrequency;A(2,1)=-NatualFrequency*e_t*s/sqrt(1-Damp*Damp);A(2,2)=e_t*(-s*Damp/sqrt(1-Damp*Damp)+c);d_f=(2*Damp^2-1)/(NatualFrequency^2*Dt);d_3t=Damp/(NatualFrequency^3*Dt);B=zeros(2,2);B(1,1)=e_t*((d_f+Damp/NatualFrequency)*s/DampFrequency+(2*d_3t+1/NatualFrequency^2)*c)-2*d_3 t;B(1,2)=-e_t*(d_f*s/DampFrequency+2*d_3t*c)-1/NatualFrequency^2+2*d_3t;B(2,1)=e_t*((d_f+Damp/NatualFrequency)*(c-Damp/sqrt(1-Damp^2)*s)-(2*d_3t+1/NatualFrequency^2 )*(DampFrequency*s+Damp*NatualFrequency*c))+1/(NatualFrequency^2*Dt);B(2,2)=e_t*(1/(NatualFrequency^2*Dt)*c+s*Damp/(NatualFrequency*DampFrequency*Dt))-1/(NatualF requency^2*Dt);for i=1:(N-1) %根据地震记录,计算不同的反应Displace(i+1)=A(1,1)*Displace(i)+A(1,2)*Velocity(i)+B(1,1)*Accelerate(i)+B(1,2)*Accelerate(i +1);Velocity(i+1)=A(2,1)*Displace(i)+A(2,2)*Velocity(i)+B(2,1)*Accelerate(i)+B(2,2)*Accelerate(i +1);AbsAcce(i+1)=-2*Damp*NatualFrequency*Velocity(i+1)-NatualFrequency^2*Displace(i+1);endMaxD(1,t)=max(abs(Displace));MaxV(1,t)=max(abs(Velocity));if T==MaxA(1,t)=max(abs(Accelerate));elseMaxA(1,t)=max(abs(AbsAcce));endDisplace=zeros(1,N);%初始化各储存向量，避免下次不同周期计算时引用到前一个周期的结果Velocity=zeros(1,N);AbsAcce=zeros(1,N);t=t+1;End% ***********PLOT***********close allfigure %绘制地震记录图plot(time(:),Accelerate(:))title('PEER STRONG MOTION DATABASE RECORD')xlabel('time(s)')ylabel('acceleration(g)')gridfigure %绘制位移反应谱plot(TA,MaxD(1,:),'',TA,MaxD(2,:),'-r',TA,MaxD(3,:),':k')title('Displacement')xlabel('Tn(s)')ylabel('Displacement(m)')legend('ζ=')Gridfigure %绘制速度反应谱plot(TA,MaxV(1,:),'',TA,MaxV(2,:),'-r',TA,MaxV(3,:),':k')title('Velocity')xlabel('Tn(s)')ylabel('velocity(m/s)')legend('ζ=')Gridfigure %绘制绝对加速度反应谱plot(TA,MaxA(1,:),'',TA,MaxA(2,:),'-r',TA,MaxA(3,:),':k')title('Absolute Acceleration')xlabel('Tn(s)')ylabel('absolute acceleration(m/s^2)')legend('ζ=')Grid3 运行的结果得到的反应谱图2 位移反应谱图3 速度反应谱图4 加速度反应谱一、反应谱生成地震波1所取的反应谱为上海市设计反应谱图5 上海市设计反应谱2反应谱取值程序为：%%规范反应谱取值程序参照01年抗震规范function rs_z=r_s_1(pl,zn,ld,cd,fz) %%%pl 圆频率,zn阻尼比,ld烈度,cd场地类型,场地分组fz %%%%烈度选择if ld==6arfmax=;endif ld==7arfmax=;endif ld==8arfmax=;endif ld==9arfmax=;end%%%%场地类别，设计地震分组选择if cd==1if fz==1Tg=;endif fz==2Tg=;endif fz==3Tg=;endendif cd==2if fz==1Tg=;endif fz==2Tg=;endif fz==3Tg=;endendif cd==3if fz==1Tg=;endif fz==2Tg=;endif fz==3Tg=;endendif cd==4if fz==1Tg=;endif fz==2Tg=;endif fz==3Tg=;endend%%%%%%%%%ceita=zn; %%%%%阻尼比lmt1=+/8;if lmt1<0lmt1=0;endlmt2=1+/+*ceita);if lmt2<lmt2=;endsjzs=+/+5*ceita);%%%%%分段位置 T1 T2 T3T1=;T2=Tg;T3=5*Tg;T_jg=2*pi./pl;%%%% 第一段 0～T1if T_jg<=T1arf_jg=*arfmax+(lmt2**arfmax)/*T_jg;end%%%% 第二段 T1～T2if T1<T_jg&T_jg<=T2arf_jg=lmt2*arfmax;end%%%% 第三段 T2~T3if T2<T_jg&T_jg<=T3arf_jg=((Tg/T_jg)^sjzs)*lmt2*arfmax;end%%%% 第四段 T3～if T3<T_jg&T_jg<=arf_jg=(lmt2*^sjzs-lmt1*(T_jg-5*Tg))*arfmax; end%%%% 第五段～if <T_jgarf_jg=(lmt2*^sjzs-lmt1**Tg))*arfmax;end%%%%%%反应谱值拟加速度值rs_z=arf_jg*;end3生成人造地震波主程序：%%%主程序%%%%%%%%确定需要控制的反应谱Sa（T）(T=T1,...,TM)的坐标点数M，反应谱控制容差rc Tyz=[::,::,::];rc=;nTyz=length(Tyz);ceita=;%%%阻尼比：for i=1:nTyzSyz(i)=r_s_1(2*pi/Tyz(i),ceita,8,2,1); %%%%8度，2类场地，第1地震分组end%%%%%% 变换的频率差：2*pi*(可以保证长周期项5s附近有5项三角级数)；%%%%频率变化范围 N1=30, 30**2*pi ;N2=3000, 5000**2*piplc=2*pi*;pl=30**2*pi:*2*pi:10000**2*pi;npl=length(pl);P=; %%%保证率%%%%%%人造地震动持续时间40s，时间间隔：Td=40;dt=;t=0::40;nt=length(t);%%%%%%% 衰减包络函数t1=8; %%%%上升段t2=8+24; %%%%%平稳段; 下降段则为40－32＝8sc=; %%%%衰减段参数for i=1:ntif t(i)<=t1f(i)=(t(i)/t1)^2;endif t(i)>t1 & t(i)<t2f(i)=1;endif t(i)>=t2f(i)=exp(-c*(t(i)-t2));endend%%%%%%% 反应谱转换功率谱for i=1:nplSw(i)=(2*ceita/(pi*pl(i)))*r_s_1(pl(i),ceita,8,2,1)^2/(-2*log(-1*pi*log(P)/(pl(i)*Td))); Aw(i)=sqrt(4*Sw(i)*plc);end%%%%%%%%%%%%%% 合成地震动at=zeros(nt,1);atj=zeros(nt,1);for i=1:nplfai(i)=rand(1)*2*pi;for j=1:ntatj(j)=f(j)*Aw(i)*real(exp(sqrt(-1)*(pl(i)*t(j)+fai(i))));endat=at+atj;end%%%%%%% 计算反应谱验证是否满足rc在5%的要求,需要时程动力分析%%%%%%%%%%%% response spectra of callidar%%%%%%% parameterg=;m=1;x0=0;v0=0;ww=2*pi./Tyz;%%%%%%%% loadag=at; %%%%%%%修改%%%%%%% solutionfor y=1:nTyzz=;w=ww(y);c=2*z*w;k=w^2;for i=1:nt-1p(i)=-ag(i+1)+ag(i);a0=m\(-ag(i)-c*v0-k*x0);kk=k+(dt^2)\(6*m)+dt\(3*c);pp=p(i)+m*(dt\(6*v0)+3*a0)+c*(3*v0+2\(dt*a0));dx=kk\pp;dv=dt\(3*dx)-3*v0-2\(dt*a0);x1=x0+dx;x0=x1;v1=v0+dv;v0=v1;as(i)=a0;as(i)=as(i)+ag(i);vs(i)=v0;xs(i)=x0;endmaxas(y)=max(as);maxvs(y)=max(vs);maxxs(y)=max(xs);endfor i=1:nTyzrspa(i)=maxas(i);end%%%%%%% 比较容差for i=1:nTyzrcrsp(i)=abs(rspa(i)-Syz(i))/max(Syz(:));endjsnum=1;while max(rcrsp(:))>rc%%%%%循环体函数blxs=Syz./rspa;for xsxs=1:nplif 2*pi/pl(xsxs)<Tyz(1)blxs1(xsxs)=blxs(1);endfor sxsx=1:nTyz-1if (2*pi/pl(xsxs)>=Tyz(sxsx)) & (2*pi/pl(xsxs)<=Tyz(sxsx+1))blxs1(xsxs)=blxs(sxsx)+(blxs(sxsx+1)-blxs(sxsx))*(2*pi/pl(xsxs)-Tyz(sxsx))/(Tyz(sxsx+1)-Tyz(sxsx));endendif 2*pi/pl(xsxs)>Tyz(nTyz)blxs1(xsxs)=blxs(nTyz);endendAw=Aw.*blxs1;%%%%%%%%%%%%%% 合成地震动at=zeros(nt,1);atj=zeros(nt,1);for i=1:nplfor j=1:ntatj(j)=f(j)*Aw(i)*real(exp(sqrt(-1)*(pl(i)*t(j)+fai(i))));endat=at+atj;end%%%%%%% 计算反应谱验证是否满足rc在5%的要求%%%%%%%%%%%% response spectra of callidar%%%%%%% parameterg=;m=1;x0=0;v0=0;ww=2*pi./Tyz;%%%%%%%% loadag=at; %%%%%%%修改%%%%%%% solutionfor y=1:nTyzz=;w=ww(y);c=2*z*w;k=w^2;for i=1:nt-1p(i)=-ag(i+1)+ag(i);a0=m\(-ag(i)-c*v0-k*x0);kk=k+(dt^2)\(6*m)+dt\(3*c);pp=p(i)+m*(dt\(6*v0)+3*a0)+c*(3*v0+2\(dt*a0)); dx=kk\pp;dv=dt\(3*dx)-3*v0-2\(dt*a0);x1=x0+dx;x0=x1;v1=v0+dv;v0=v1;as(i)=a0;as(i)=as(i)+ag(i);vs(i)=v0;xs(i)=x0;endmaxas(y)=max(as);maxvs(y)=max(vs);maxxs(y)=max(xs);endfor i=1:nTyzrspa(i)=maxas(i);end%%%%%%% 比较容差for i=1:nTyzrcrsp(i)=abs(rspa(i)-Syz(i))/max(Syz(:));endjsnum=jsnum+1max(rcrsp(:))end%%%%%%% 最终的反应谱与规范谱%%%%%%%%%%%% response spectra of callidar%%%%%%% parameter%% Tjs=::6;%% nTjs=length(Tjs);g=;m=1;x0=0;v0=0;ww=2*pi./Tyz;%%%%%%%% loadag=at; %%%%%%%修改%%%%%%% solutionfor y=1:nTyzz=;w=ww(y);c=2*z*w;k=w^2;for i=1:nt-1p(i)=-ag(i+1)+ag(i);a0=m\(-ag(i)-c*v0-k*x0);kk=k+(dt^2)\(6*m)+dt\(3*c);pp=p(i)+m*(dt\(6*v0)+3*a0)+c*(3*v0+2\(dt*a0)); dx=kk\pp;dv=dt\(3*dx)-3*v0-2\(dt*a0);x1=x0+dx;x0=x1;v1=v0+dv;v0=v1;as(i)=a0;as(i)=as(i)+ag(i);vs(i)=v0;xs(i)=x0;endmaxas(y)=max(as);maxvs(y)=max(vs);maxxs(y)=max(xs);endfor i=1:nTyzrspa(i)=maxas(i)/g;rspa_S(i)=r_s_1(2*pi/Tyz(i),ceita,8,2,1)/g;endsubplot(2,1,1);plot(t,at);subplot(2,1,2);plot(Tyz,rspa);hold on;plot(Tyz,rspa_S);4生成的人造地震波如图所示。

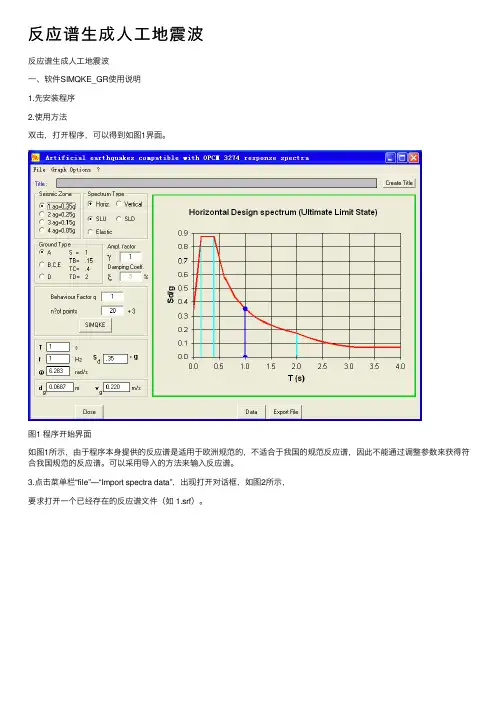
反应谱⽣成⼈⼯地震波反应谱⽣成⼈⼯地震波⼀、软件SIMQKE_GR使⽤说明1.先安装程序2.使⽤⽅法双击，打开程序，可以得到如图1界⾯。

图1 程序开始界⾯如图1所⽰，由于程序本⾝提供的反应谱是适⽤于欧洲规范的，不适合于我国的规范反应谱，因此不能通过调整参数来获得符合我国规范的反应谱。

可以采⽤导⼊的⽅法来输⼊反应谱。

3.点击菜单栏“file”—“Import spectra data”，出现打开对话框，如图2所⽰，要求打开⼀个已经存在的反应谱⽂件（如 1.srf）。

图2 导⼊反应谱⽂件对话框4.⽂件格式如下所⽰（红字部分不能修改，注意反应谱单位为g），下⾯部分可以替换。

response spectrumtime(s) acc(g)0 0.12150.01 0.136350.02 0.15120.03 0.166050.04 0.18090.05 0.195750.06 0.21060.07 0.225450.08 0.24030.09 0.255150.1 0.270.15 0.270.2 0.270.25 0.270.3 0.270.35 0.270.4 0.270.45 0.270.5 0.2430.7 0.173571429 0.8 0.1518750.9 0.1351 0.12151.1 0.110454545 1.2 0.101251.3 0.093461538 1.4 0.086785714 1.5 0.0811.6 0.0759375 1.7 0.071470588 1.8 0.06751.9 0.0639473682 0.060752.1 0.057857143 2.2 0.055227273 2.3 0.052826087 2.4 0.050625 2.5 0.04862.6 0.046730769 2.7 0.0452.8 0.0433928572.9 0.0418965523 0.04053.1 0.039193548 3.2 0.03796875 3.3 0.036818182 3.4 0.035735294 3.5 0.034714286 3.6 0.033753.7 0.032837838 3.8 0.0319736843.9 0.0311538464 0.0303754.1 0.029634146 4.2 0.028928571 4.3 0.028255814 4.4 0.027613636 4.5 0.0274.6 0.026413043 4.7 0.025851064 4.8 0.02531255 0.02435.1 0.023823529 5.2 0.023365385 5.3 0.022924528 5.4 0.02255.5 0.022090909 5.6 0.021696429 5.7 0.021315789 5.8 0.0209482765.9 0.020593226 0.020256.1 0.019918033 6.2 0.019596774 6.3 0.019285714 6.4 0.018984375 6.5 0.018692308 6.6 0.018409091 6.7 0.018134328 6.8 0.0178676476.9 0.0176086967 0.0173571437.1 0.017112676 7.2 0.016875 7.3 0.016643836 7.4 0.016418919 7.5 0.01627.6 0.015986842 7.7 0.015779221 7.8 0.0155769237.9 0.0153797478 0.01518758.1 0.0158.2 0.014817073 8.3 0.014638554 8.4 0.014464286 8.5 0.014294118 8.6 0.014127907 8.7 0.013965517 8.8 0.013806818 8.9 0.0136516859.1 0.013351648 9.2 0.0132065229.4 0.0129255329.5 0.0127894749.6 0.012656259.7 0.0125257739.8 0.0123979599.9 0.01227272710 0.01215选择桌⾯上的“1.srf”⽂件，打开后的程序界⾯如图3所⽰：图3 打开反应谱⽂件1.srf⽂件后的程序界⾯点击图3中的“SIMQKE”按钮，得到如图4所⽰的界⾯。

姓名：郭 勇 学号：022*******人工地震波生成程序简介一、 程序设计内容及方法1、程序内容本程序根据特征周期、水平地震波影响系数最大值和地震波幅值等初始条件生成人工地震波，为结构动力分析的时程分析法提供地震波来源。

2、程序设计方法(1) 理论依据本程序采用三角级数法生成人工地震波。

对于给定的功率谱密度函数()x S ω，按照下面的公式可以方便的生成以()x S ω为功率谱密度函数、均值为零的高斯平稳过程()a t 。

1()cos()Nk k k k a t C t ωϕ==+∑ (1)式中：12[4()]()/1()2k x k u l k l C S N k ωωωωωωωω⎫⎪=∆⎪∆=-⎬⎪⎪=+-∆⎭(2)k ϕ为(0,2)π内均匀分布的随机相角；u ω，l ω分别为正ω域内的上、下限值，即认为()x S ω的有效功率在(,)u l ωω范围内，而范围外的()x S ω值可视为零。

为了反映地面运动的非平稳性，采用包络函数()f t 乘以平稳过程()a t ，()()()x t f t a t = (3)(3)式即为人工地震波模型。

()f t 可根据下式确定：2221112()233/01()0c t t t t t t t t t f t e t t t t t T--⎧≤<⎪≤<⎪=⎨≤<⎪⎪<≤⎩ (4)式中：c 为衰减系数，通常取值范围为0.1~1.0，本程序取0.15；1t ，2t 和3t 根据不同实际情况取值，T 为地震波持时，本程序取1t ，2t 分别为4s ，15s ，3t 和T 均为40s 。

本程序采用《建筑抗震设计规范》(GB50011-2001)中的反应谱作为目标谱，通过Kaul 提出的平稳过程反应谱与功率谱的近似关系22()[()]/[2ln(ln )]T x k a k kk dS S p T ξπωωπωω=--(5) 式中：()Tak S ω为规范反应谱；ξ为阻尼比；d T 为地震动持时；p 为反应不超过反应谱值的概率，本程序取0.85。