八层框架的地震响应计算和人工波生成的matlab实现及所需曲线图的自动存储

2008年第6期总第120期福 建 建 筑F u j i a nA r c h i t e c t u r e ＆C o n s t r u c t i o nN o 6·2008V o l ·120基于M a t l a b 求解建筑结构地震响应的时程分析法孟宪萍(开封市供水总公司　475004)摘　要:本文基于m a t l a b 阐述了我国《建筑抗震设计规范》(G B 50011-2001)规定的求解建筑结构地震响应的时程分析法,应用m a t l a b 语言编制了时程分析法求解建筑结构地震响应的计算程序,并以一三层钢筋混凝土结构为工程算例,应用基于m a t l a b 的时程分析法进行结构的地震响应计算。

结果表明,基于m a t l a b 的时程分析计算效率较高。

关键词:M A T L A B 地震响应　时程分析法中图分类号:T U 312+.1 文献标识码:A 文章编号:1004-6135(2008)06-0038-03T h e t i m e -h i s t o r y m e t h o db a s e d o nm a t l a b o f r e s o l v i n g t h e e a r t h q u a k e r e s p o n s e o f t h e s t r u c t u r e sM e n g X i a n p i n g(K a i f e n g Wa t e r S u p p l y C o m p a n y 475004)A b s t r a c t :I nt h i s p a p e r ,t h e t i m e -h i s t o r y m e t h o dw h i c h i s m e n t i o n e d i n t h e c o d e f o r s e i s m i c d e s i g n o f b u i l d i n g s (GB 50011-2001)t or e s o l v e t h e e a r t h q u a k e r e s p o n s e o f t h e s t r u c t u r e s i s d i s c u s s e d b a s e d o nm a t l a b .T h e c a l c u l a t i o np r o g r a m s o f t h et i m e -h i s t o r y m e t h o da r e w o r k e do u t u s i n g t h e l a n g u a g e m a t l a b .T a k i n g a t h r e es t o r y r e i n f o r c e d c o n c r e t e f r a m e s t r u c t u r e a s a ne x a m p l e ,t h e e a r t h q u a k e r e s p o n s e o f t h e s t r u c t u r e i s r e s o l v e d b y u s i n g t h e c a l c u l a t i o n p r o g r a m s o f t h e t i m e -h i s t o r y m e t h o d .T h e r e s u l t i n d i c a t e s t h a t T h e t i m e -h i s t o r y m e t h o d b a s e do n m a t l a bo f r e s o l v i n gt h e e a r t h q u a k e r e s p o n s e o f t h e s t r u c t u r e s i s e f f i c i e n t .K e y w o r d s :M A T L A B e a r t h q u a k e r e s p o n s e t i m e -h i s t o r y a n a l y s i s m e t h od 作者简介:孟宪萍,女,1966年出生,主要从事建筑结构设计及建筑咨询。

地震工程学作业课程名称:地震工程学______ 指导老师:_______翟永梅_________ 姓名:史先飞________ 学号:1232627________一、地震波生成反应谱1 所取的地震波为Elcentro地震波加速度曲线，如图1所示。

图1 Elcentro地震波加速度曲线2 所调用的Matlab程序为：% ***********读入地震记录***********ElCentro;Accelerate= ElCentro(:,1)*9.8067;%单位统一为m和sN=length(Accelerate);%N 读入的记录的量time=0:0.005:(N-1)*0.005; %单位 s%初始化各储存向量Displace=zeros(1,N); %相对位移Velocity=zeros(1,N); %相对速度AbsAcce=zeros(1,N); %绝对加速度% ***********A,B矩阵***********Damp=0.02; %阻尼比0.02TA=0.0:0.05:6; %TA=0.000001:0.02:6; %结构周期Dt=0.005; %地震记录的步长%记录计算得到的反应，MaxD为某阻尼时最大相对位移，MaxV为某阻尼最大相对速度，MaxA某阻尼时最大绝对加速度，用于画图MaxD=zeros(3,length(TA));MaxV=zeros(3,length(TA));MaxA=zeros(3,length(TA));t=1;for T=0.0:0.05:6NatualFrequency=2*pi/T ; %结构自振频率DampFrequency=NatualFrequency*sqrt(1-Damp*Damp); %计算公式化简e_t=exp(-Damp*NatualFrequency*Dt);s=sin(DampFrequency*Dt);c=cos(DampFrequency*Dt);A=zeros(2,2);A(1,1)=e_t*(s*Damp/sqrt(1-Damp*Damp)+c);A(1,2)=e_t*s/DampFrequency;A(2,1)=-NatualFrequency*e_t*s/sqrt(1-Damp*Damp);A(2,2)=e_t*(-s*Damp/sqrt(1-Damp*Damp)+c);d_f=(2*Damp^2-1)/(NatualFrequency^2*Dt);d_3t=Damp/(NatualFrequency^3*Dt);B=zeros(2,2);B(1,1)=e_t*((d_f+Damp/NatualFrequency)*s/DampFrequency+(2*d_3t+1/NatualFrequency^2)*c)-2*d_3 t;B(1,2)=-e_t*(d_f*s/DampFrequency+2*d_3t*c)-1/NatualFrequency^2+2*d_3t;B(2,1)=e_t*((d_f+Damp/NatualFrequency)*(c-Damp/sqrt(1-Damp^2)*s)-(2*d_3t+1/NatualFrequency^2 )*(DampFrequency*s+Damp*NatualFrequency*c))+1/(NatualFrequency^2*Dt);B(2,2)=e_t*(1/(NatualFrequency^2*Dt)*c+s*Damp/(NatualFrequency*DampFrequency*Dt))-1/(NatualF requency^2*Dt);for i=1:(N-1) %根据地震记录,计算不同的反应Displace(i+1)=A(1,1)*Displace(i)+A(1,2)*Velocity(i)+B(1,1)*Accelerate(i)+B(1,2)*Accelerate(i +1);Velocity(i+1)=A(2,1)*Displace(i)+A(2,2)*Velocity(i)+B(2,1)*Accelerate(i)+B(2,2)*Accelerate(i +1);AbsAcce(i+1)=-2*Damp*NatualFrequency*Velocity(i+1)-NatualFrequency^2*Displace(i+1);endMaxD(1,t)=max(abs(Displace));MaxV(1,t)=max(abs(Velocity));if T==0.0MaxA(1,t)=max(abs(Accelerate));elseMaxA(1,t)=max(abs(AbsAcce));endDisplace=zeros(1,N);%初始化各储存向量，避免下次不同周期计算时引用到前一个周期的结果Velocity=zeros(1,N);AbsAcce=zeros(1,N);t=t+1;End% ***********PLOT***********close allfigure %绘制地震记录图plot(time(:),Accelerate(:))title('PEER STRONG MOTION DATABASE RECORD')xlabel('time(s)')ylabel('acceleration(g)')gridfigure %绘制位移反应谱plot(TA,MaxD(1,:),'-.b',TA,MaxD(2,:),'-r',TA,MaxD(3,:),':k')title('Displacement')xlabel('Tn(s)')ylabel('Displacement(m)')legend('ζ=0.02')Gridfigure %绘制速度反应谱plot(TA,MaxV(1,:),'-.b',TA,MaxV(2,:),'-r',TA,MaxV(3,:),':k') title('Velocity')xlabel('Tn(s)')ylabel('velocity(m/s)')legend('ζ=0.02')Gridfigure %绘制绝对加速度反应谱plot(TA,MaxA(1,:),'-.b',TA,MaxA(2,:),'-r',TA,MaxA(3,:),':k') title('Absolute Acceleration')xlabel('Tn(s)')ylabel('absolute acceleration(m/s^2)')legend('ζ=0.02')Grid3 运行的结果得到的反应谱图2 位移反应谱图3 速度反应谱图4 加速度反应谱一、反应谱生成地震波1所取的反应谱为上海市设计反应谱图5 上海市设计反应谱2反应谱取值程序为：%%规范反应谱取值程序参照01年抗震规范function rs_z=r_s_1(pl,zn,ld,cd,fz) %%%pl 圆频率,zn阻尼比,ld烈度,cd场地类型,场地分组fz %%%%烈度选择if ld==6arfmax=0.11;endif ld==7arfmax=0.23;endif ld==8arfmax=0.45;endif ld==9arfmax=0.90;end%%%%场地类别，设计地震分组选择if cd==1if fz==1Tg=0.25;endif fz==2Tg=0.30;endif fz==3Tg=0.35;endendif cd==2if fz==1Tg=0.35;if fz==2Tg=0.40;endif fz==3Tg=0.45;endendif cd==3if fz==1Tg=0.45;endif fz==2Tg=0.55;endif fz==3Tg=0.65;endendif cd==4if fz==1Tg=0.65;endif fz==2Tg=0.75;endif fz==3Tg=0.90;endend%%%%%%%%%ceita=zn; %%%%%阻尼比lmt1=0.02+(0.05-ceita)/8;if lmt1<0lmt1=0;endlmt2=1+(0.05-ceita)/(0.06+1.7*ceita); if lmt2<0.55lmt2=0.55;endsjzs=0.9+(0.05-ceita)/(0.5+5*ceita); %%%%%分段位置 T1 T2 T3T1=0.1;T2=Tg;T_jg=2*pi./pl;%%%% 第一段 0～T1if T_jg<=T1arf_jg=0.45*arfmax+(lmt2*arfmax-0.45*arfmax)/0.1*T_jg;end%%%% 第二段 T1～T2if T1<T_jg&T_jg<=T2arf_jg=lmt2*arfmax;end%%%% 第三段 T2~T3if T2<T_jg&T_jg<=T3arf_jg=((Tg/T_jg)^sjzs)*lmt2*arfmax;end%%%% 第四段 T3～6.0if T3<T_jg&T_jg<=6.0arf_jg=(lmt2*0.2^sjzs-lmt1*(T_jg-5*Tg))*arfmax;end%%%% 第五段 6.0～if 6.0<T_jgarf_jg=(lmt2*0.2^sjzs-lmt1*(6.0-5*Tg))*arfmax;end%%%%%%反应谱值拟加速度值rs_z=arf_jg*9.8;end3生成人造地震波主程序：%%%主程序%%%%%%%%确定需要控制的反应谱Sa（T）(T=T1,...,TM)的坐标点数M，反应谱控制容差rc Tyz=[0.04:0.016:0.1,0.15:0.05:3.0,3.2:0.05:5.0];rc=0.06;nTyz=length(Tyz);ceita=0.035;%%%阻尼比：0.035for i=1:nTyzSyz(i)=r_s_1(2*pi/Tyz(i),ceita,8,2,1); %%%%8度，2类场地，第1地震分组end%%%%%% 变换的频率差：2*pi*0.005(可以保证长周期项5s附近有5项三角级数)；%%%%频率变化范围 N1=30, 30*0.005*2*pi ;N2=3000, 5000*0.005*2*piplc=2*pi*0.005;pl=30*0.005*2*pi:0.005*2*pi:10000*0.005*2*pi;npl=length(pl);P=0.9; %%%保证率%%%%%%人造地震动持续时间40s，时间间隔：0.02sTd=40;dt=0.02;t=0:0.02:40;nt=length(t);%%%%%%% 衰减包络函数t1=8; %%%%上升段t2=8+24; %%%%%平稳段; 下降段则为40－32＝8sc=0.6; %%%%衰减段参数for i=1:ntif t(i)<=t1f(i)=(t(i)/t1)^2;endif t(i)>t1 & t(i)<t2f(i)=1;endif t(i)>=t2f(i)=exp(-c*(t(i)-t2));endend%%%%%%% 反应谱转换功率谱for i=1:nplSw(i)=(2*ceita/(pi*pl(i)))*r_s_1(pl(i),ceita,8,2,1)^2/(-2*log(-1*pi*log(P)/(pl(i)*Td))); Aw(i)=sqrt(4*Sw(i)*plc);end%%%%%%%%%%%%%% 合成地震动at=zeros(nt,1);atj=zeros(nt,1);for i=1:nplfai(i)=rand(1)*2*pi;for j=1:ntatj(j)=f(j)*Aw(i)*real(exp(sqrt(-1)*(pl(i)*t(j)+fai(i))));endat=at+atj;end%%%%%%% 计算反应谱验证是否满足rc在5%的要求,需要时程动力分析%%%%%%%%%%%% response spectra of callidar%%%%%%% parameterg=9.8;m=1;x0=0;v0=0;ww=2*pi./Tyz;%%%%%%%% loadag=at; %%%%%%%修改%%%%%%% solutionfor y=1:nTyzz=0.037;w=ww(y);c=2*z*w;k=w^2;for i=1:nt-1p(i)=-ag(i+1)+ag(i);a0=m\(-ag(i)-c*v0-k*x0);kk=k+(dt^2)\(6*m)+dt\(3*c);pp=p(i)+m*(dt\(6*v0)+3*a0)+c*(3*v0+2\(dt*a0)); dx=kk\pp;dv=dt\(3*dx)-3*v0-2\(dt*a0);x1=x0+dx;x0=x1;v1=v0+dv;v0=v1;as(i)=a0;as(i)=as(i)+ag(i);vs(i)=v0;xs(i)=x0;endmaxas(y)=max(as);maxvs(y)=max(vs);maxxs(y)=max(xs);endfor i=1:nTyzrspa(i)=maxas(i);end%%%%%%% 比较容差for i=1:nTyzrcrsp(i)=abs(rspa(i)-Syz(i))/max(Syz(:));endjsnum=1;while max(rcrsp(:))>rc%%%%%循环体函数blxs=Syz./rspa;for xsxs=1:nplif 2*pi/pl(xsxs)<Tyz(1)blxs1(xsxs)=blxs(1);endfor sxsx=1:nTyz-1if (2*pi/pl(xsxs)>=Tyz(sxsx)) & (2*pi/pl(xsxs)<=Tyz(sxsx+1))blxs1(xsxs)=blxs(sxsx)+(blxs(sxsx+1)-blxs(sxsx))*(2*pi/pl(xsxs)-Tyz(sxsx))/(Tyz(sxsx+1)-Tyz(sxsx));endendif 2*pi/pl(xsxs)>Tyz(nTyz)blxs1(xsxs)=blxs(nTyz);endendAw=Aw.*blxs1;%%%%%%%%%%%%%% 合成地震动at=zeros(nt,1);atj=zeros(nt,1);for i=1:nplfor j=1:ntatj(j)=f(j)*Aw(i)*real(exp(sqrt(-1)*(pl(i)*t(j)+fai(i))));endat=at+atj;end%%%%%%% 计算反应谱验证是否满足rc在5%的要求%%%%%%%%%%%% response spectra of callidar%%%%%%% parameterg=9.8;m=1;x0=0;v0=0;ww=2*pi./Tyz;%%%%%%%% loadag=at; %%%%%%%修改%%%%%%% solutionfor y=1:nTyzz=0.037;w=ww(y);c=2*z*w;k=w^2;for i=1:nt-1p(i)=-ag(i+1)+ag(i);a0=m\(-ag(i)-c*v0-k*x0);kk=k+(dt^2)\(6*m)+dt\(3*c);pp=p(i)+m*(dt\(6*v0)+3*a0)+c*(3*v0+2\(dt*a0)); dx=kk\pp;dv=dt\(3*dx)-3*v0-2\(dt*a0);x1=x0+dx;x0=x1;v1=v0+dv;v0=v1;as(i)=a0;as(i)=as(i)+ag(i);vs(i)=v0;xs(i)=x0;endmaxas(y)=max(as);maxvs(y)=max(vs);maxxs(y)=max(xs);endfor i=1:nTyzrspa(i)=maxas(i);end%%%%%%% 比较容差for i=1:nTyzrcrsp(i)=abs(rspa(i)-Syz(i))/max(Syz(:));endjsnum=jsnum+1max(rcrsp(:))end%%%%%%% 最终的反应谱与规范谱%%%%%%%%%%%% response spectra of callidar%%%%%%% parameter%% Tjs=0.05:0.01:6;%% nTjs=length(Tjs);g=9.8;m=1;x0=0;v0=0;ww=2*pi./Tyz;%%%%%%%% loadag=at; %%%%%%%修改%%%%%%% solutionfor y=1:nTyzz=0.037;w=ww(y);c=2*z*w;k=w^2;for i=1:nt-1p(i)=-ag(i+1)+ag(i);a0=m\(-ag(i)-c*v0-k*x0);kk=k+(dt^2)\(6*m)+dt\(3*c);pp=p(i)+m*(dt\(6*v0)+3*a0)+c*(3*v0+2\(dt*a0));dx=kk\pp;dv=dt\(3*dx)-3*v0-2\(dt*a0);x1=x0+dx;x0=x1;v1=v0+dv;v0=v1;as(i)=a0;as(i)=as(i)+ag(i);vs(i)=v0;xs(i)=x0;endmaxas(y)=max(as);maxvs(y)=max(vs);maxxs(y)=max(xs);endfor i=1:nTyzrspa(i)=maxas(i)/g;rspa_S(i)=r_s_1(2*pi/Tyz(i),ceita,8,2,1)/g;endsubplot(2,1,1);plot(t,at);subplot(2,1,2);plot(Tyz,rspa);hold on;plot(Tyz,rspa_S);4生成的人造地震波如图所示。

利用MATLAB,plot等软件来实现地震资料的处理
陶泽丹;田先德
【期刊名称】《内蒙古石油化工》
【年(卷),期】2010(036)024
【摘要】随着石油、天然气工业的发展,各种针对石油天然气勘探的软件不断出现,这些大型的商业软件虽然有很多参数的控制,但是还是不能随着研究人员个人的意愿随意的将个人的一些创新运用到地震资料的处理中去.针对这样的情况,可以考虑利用Matlab软件来将研究人员的思路和创新编成算法,然后通过
Plot,Seisplot,segy,SeisFormat等小软件来对Matlab处理后的资料进行显示,变成熟悉的、直观的地震记录的形式,然后不断的对算法进行优化,直到得到满意的结果.
【总页数】2页(P50-51)
【作者】陶泽丹;田先德
【作者单位】中国海洋大学海洋地球科学学院;中国海洋大学海洋地球科学学院【正文语种】中文
【中图分类】P631.4+43;TP399
【相关文献】
1.Matlab软件在测井资料处理中的应用
2.用MATLAB实现滤波器对数字地震资料处理初探
3.利用地震资料解释系统实现非地震资料的解释
4.利用小波变换实现
地震资料分频去噪处理5.利用MATLAB信号处理工具箱SPTool完成地震资料滤波处理
因版权原因，仅展示原文概要，查看原文内容请购买。

基于Matlab数值方法的结构地震反应分析
胡涛
【期刊名称】《工程建设与设计》
【年(卷),期】2014(000)007
【摘要】通过Matlab语言编写了3个时程分析程序,分别采用Duhamel积分法、Newmark-beta法及Rong-kuta法.在求解多自由度结构体系时,采用振型分解法
将多自由度结构体系问题转化为多个广义单自由度结构体系问题,然后对所得计算
结果按一定准则进行叠加,求出结构地震反应.首先,对莱3层钢筋混凝土框架结构进行时程分析,计算结果与已有文献吻合较好,证明了所编程序的正确性;其次,通过对计算时间的分析对比,表明Rong-kuta法效率最高.论文可为相关工程及设计人员在
选择计算方法时提供参考.
【总页数】4页(P65-67,70)
【作者】胡涛
【作者单位】香港华艺设计顾问(深圳)有限公司,广东深圳518031
【正文语种】中文
【中图分类】TU352.11
【相关文献】
1.基于 CFD/CSD 耦合的结构几何非线性静气动弹性数值方法研究 [J], 聂雪媛;黄程德;杨国伟
2.基于MATLAB数值方法在机械工程领域的应用分析 [J], 胡享平;黄亚宇
3.基于Matlab的开关变换器混沌研究数值方法 [J], 王诗兵;周宇飞;陈军宁
4.线性方程组的几种数值方法的MATLAB程序 [J], 吴专保
5.基于Matlab的数值分析算法演示系统开发——非线性方程的数值方法 [J], 柯双
因版权原因，仅展示原文概要，查看原文内容请购买。

Matlab在地震工程中的应用技巧介绍：地震工程是一个重要的领域，它研究的是地震对建筑物、基础设施以及土地的影响。

在地震分析中，工程师经常需要进行数据处理、模拟和可视化。

Matlab是一种被广泛用于科学计算和工程应用的编程语言和环境，它具有强大的数据处理和可视化功能，因此在地震工程中有很多应用技巧可以利用。

一、数据处理1.导入和导出数据：Matlab提供了丰富的数据导入和导出函数，能够方便地读取和保存各种文件格式，如文本文件、Excel文件以及常用的数据格式如CSV、MAT等。

对于地震工程中的实验数据或模拟结果，可以轻松地导入到Matlab中进行后续的处理和分析。

2.数据清洗和预处理：地震数据通常包含噪声和无效信息，我们需要对数据进行清洗和预处理以提高后续分析的准确性。

Matlab提供了一系列的数据处理函数，如滤波、去噪以及插补等，可以帮助我们准确地提取有用的信息。

3.数据分析和统计：地震数据的分析和统计是地震工程中常见的任务，如频谱分析、功率谱密度估计、相关性分析等。

Matlab中拥有丰富的统计工具箱和信号处理工具箱，可以帮助工程师快速进行各种数据分析和统计。

二、模拟和建模1.地震动模拟：在地震工程中，我们通常需要模拟地震动的时程，以评估该地震对结构物的影响。

Matlab提供了众多的地震动模拟函数和工具箱，可以根据所需的地震参数，生成符合各种地震动模型的时程。

2.结构动力学模拟：Matlab具有强大的数值计算和模拟能力，可以进行结构的动力学模拟，从而预测结构在地震中的行为。

工程师可以利用Matlab进行结构的有限元建模和动力响应分析，从而评估结构的抗震性能。

3.参数识别和优化：对于地震工程中复杂的结构体系，我们常常需要辨识结构的参数以及优化结构的设计。

Matlab提供了多种参数识别和优化工具，如曲线拟合、参数标定以及遗传算法等，可以帮助工程师快速而准确地确定结构参数。

三、可视化与结果展示1.绘图和图像处理：Matlab提供了丰富的绘图函数和图像处理工具，可以将地震数据或模拟结果进行可视化展示。

Matlab在地震模拟和结构动力学中的应用地震是自然界中一种具有巨大破坏力的现象，对于建筑结构的性能和安全性具有重要影响。

为了确保建筑物的安全，我们需要对地震作用下的结构响应进行准确可靠的研究和分析。

在这方面，Matlab作为一种强大的科学计算软件，广泛应用于地震模拟和结构动力学领域。

一、地震模拟地震模拟是一种利用计算模型来模拟地震过程的方法。

Matlab提供了强大的数值计算和图形化能力，使得地震模拟成为可能。

首先，Matlab提供了丰富的数值计算函数和工具箱，可以进行地震波的生成和处理。

通过使用这些函数，我们可以从已有地震记录中提取出合适的地震波形，或者生成符合特定要求的地震波。

得到地震波数据后，可以通过Matlab的图形化能力，将地震波形以图表的形式展示出来，更加直观地理解地震波的特征和动态。

其次，Matlab还提供了各种数值方法和算法，用于求解地震动力学方程。

通过建立适当的数学模型，结合地震波数据，可以利用Matlab进行地震模拟。

这些数值方法和算法包括有限元法、有限差分法、时程分析等，可以根据实际问题的需要，选择合适的方法进行模拟和分析。

最后，Matlab还能进行地震动力学结果的后处理和分析。

通过将模拟结果导入到Matlab中，我们可以对结构的位移响应、加速度响应和应力响应等进行详细统计和分析。

同时，我们还可以对不同模型进行对比研究，评估结构的破坏程度和性能安全性。

二、结构动力学分析结构动力学分析是研究建筑结构在地震作用下的响应和行为的一门学科。

Matlab在结构动力学分析中有着广泛的应用。

首先，Matlab提供了方便的结构建模和预处理工具。

我们可以通过Matlab编写脚本来描述结构的几何形状、材料特性和支承条件等。

结构的参数化描述和自动生成可以极大地简化建模过程，提高工作效率。

其次，Matlab提供了各种求解结构动力学方程的数值方法和算法。

结构动力学方程包括线性和非线性动力学方程，可以通过Matlab进行求解。

地震资料处理中的matlab实现摘要：一、地震资料处理的重要性二、MATLAB 在地震资料处理中的应用三、MATLAB 在地震资料处理中的优势四、MATLAB 在地震资料处理中的实际应用案例五、总结正文：地球是一个活跃的行星，地震频繁发生。

地震资料处理对于了解地震发生的原因、预测地震趋势和减少地震带来的损失具有重要意义。

MATLAB 是一种功能强大的数学软件，被广泛应用于科学计算、数据分析等领域。

在地震资料处理中，MATLAB 也发挥着重要作用。

MATLAB 在地震资料处理中的应用主要包括地震波的数值模拟、地震数据处理、地震图像处理等。

其中，地震波的数值模拟是地震资料处理的核心环节，通过数值模拟可以再现地震波的形成过程，从而揭示地震的成因。

地震数据处理是对地震资料进行采集、整理、分析的过程，目的是提取地震资料中有用的信息，为地震预测和地震工程提供依据。

地震图像处理则是将地震图像进行数字化处理，以便于进行后续的数据分析。

MATLAB 在地震资料处理中的优势主要体现在以下几个方面：首先，MATLAB 具有丰富的函数库，可以大大提高地震资料处理的效率。

其次，MATLAB 具有强大的数据处理能力，可以对地震数据进行快速、准确的处理。

最后，MATLAB 具有丰富的图形绘制功能，可以直观地展示地震数据的结果。

在地震资料处理中，MATLAB 可以应用于多个方面。

例如，可以利用MATLAB 进行地震波的数值模拟，通过模拟地震波的形成过程，从而揭示地震的成因。

可以利用MATLAB 进行地震数据处理，对地震资料进行采集、整理、分析，提取地震资料中有用的信息。

可以利用MATLAB 进行地震图像处理，将地震图像进行数字化处理，以便于进行后续的数据分析。

总的来说，MATLAB 在地震资料处理中的应用具有重要意义。

通过MATLAB，可以提高地震资料处理的效率，准确处理地震数据，直观展示地震数据的结果。

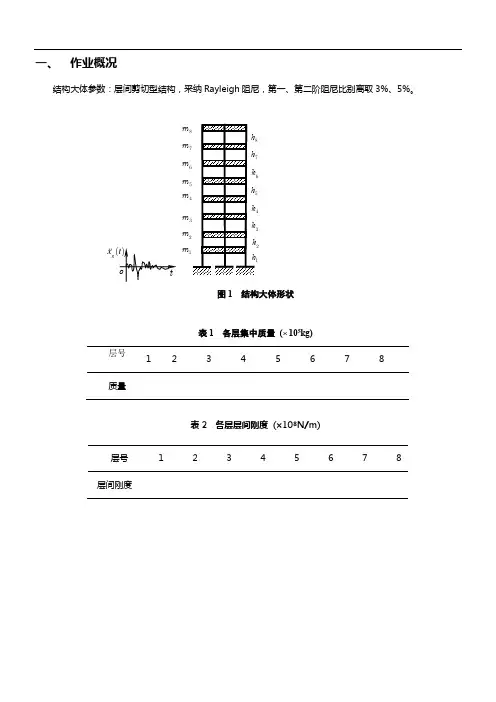
一、 作业概况结构大体参数：层间剪切型结构，采纳Rayleigh 阻尼，第一、第二阶阻尼比别离取3%、5%。

图1 结构大体形状表1 各层集中质量 ( 105kg)层号12 3 4 5 6 7 8 质量表2 各层层间刚度 (×108N/m)层号 1 2 3 4 5 6 7 8 层间刚度m m m m m m m m ()g x t二、 频率及振型计算依照层间模型的假定，能够成立结构的质量矩阵和刚度矩阵如下。

12345678000000000000000000000000000000000000000000000000000000003.400000000 3.400000000 3.200000000 3.20000 =0000 2.800000000 2.800000000 2.700000000 2.6m m m m m m m m ⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎛⎫ ⎝M 510kg ⎪⎪⎪⎪⎪⨯⎪⎪⎪⎪⎪⎪⎭11121314151617182122232425262728313233343536373841424344454647485152535455565758616263646566676871727374757677788182838485868788k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k ⎛ =⎝K 8420000002 3.8 1.8000000 1.8 3.6 1.8000000 1.8 3.6 1.8000 =10/000 1.8 3.6 1.8000000 1.8 3.4 1.6000000 1.6 3.2 1.6000000 1.6 1.6N m ⎫⎪⎪⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎭-⎛⎫ ⎪-- ⎪ ⎪-- ⎪-- ⎪⨯ ⎪-- ⎪-- ⎪ ⎪-- ⎪ ⎪-⎝⎭依照上面求得的质量、刚度矩阵，即可求解特点方程： 20KM （1）求解自振频率和阵型向量已经演变成为典型的求解矩阵特点值和特点向量的问题，特点值即为圆频率2，特点向量即为振型向量。

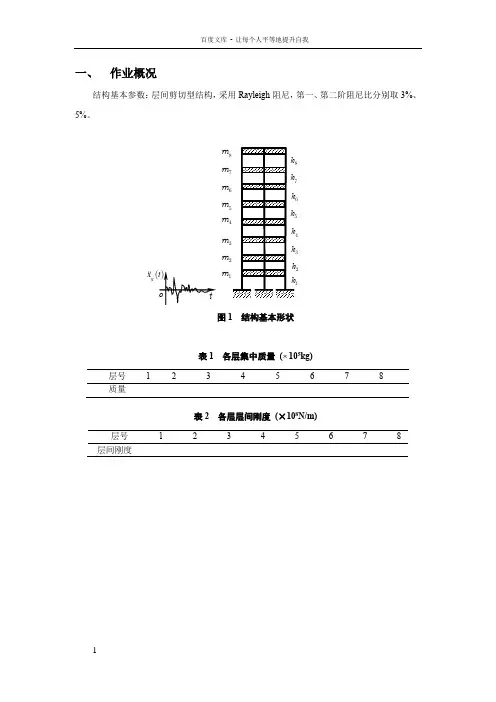
一、 作业概况结构基本参数：层间剪切型结构，采用Rayleigh 阻尼，第一、第二阶阻尼比分别取3%、5%。

图1 结构基本形状表1 各层集中质量 ( 105kg)层号 12345678质量表2 各层层间刚度 (×108N/m)层号 1 2 3 4 5 6 7 8 层间刚度m m m m m m m m ()g x t二、 频率及振型计算根据层间模型的假定，可以建立结构的质量矩阵以及刚度矩阵如下。

12345678000000000000000000000000000000000000000000000000000000003.400000000 3.400000000 3.200000000 3.20000 =0000 2.800000000 2.800000000 2.700000000 2.6m m m m m m m m ⎛⎫ ⎪ ⎪ ⎪ ⎪⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎛⎫ ⎝M 510kg ⎪⎪⎪⎪⎪⨯⎪⎪⎪⎪⎪⎪⎭ 11121314151617182122232425262728313233343536373841424344454647485152535455565758616263646566676871727374757677788182838485868788k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k ⎛ =⎝K 8420000002 3.8 1.8000000 1.8 3.6 1.8000000 1.8 3.6 1.8000 =10/000 1.8 3.6 1.8000000 1.8 3.4 1.6000000 1.6 3.2 1.6000000 1.6 1.6N m ⎫⎪⎪⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎭-⎛⎫ ⎪-- ⎪ ⎪-- ⎪-- ⎪⨯ ⎪-- ⎪-- ⎪ ⎪-- ⎪ ⎪-⎝⎭根据上面求得的质量、刚度矩阵，即可求解特征方程：20K M（1）求解自振频率以及阵型向量已经演变成为典型的求解矩阵特征值以及特征向量的问题，特征值即为圆频率2，特征向量即为振型向量。

地震资料处理中的matlab实现（原创实用版）目录1.引言2.MATLAB 在地震资料处理中的应用3.用 MATLAB 实现滤波器对数字地震资料处理4.地震资料处理的并行处理方法5.结论正文地震资料处理中的 MATLAB 实现地震是地球表面的一种自然现象，通过对地震资料的研究，可以了解地震的成因、地震波的传播规律以及地震对建筑物的影响等。

在地震资料处理中，MATLAB 作为一种强大的科学计算软件，可以提供许多有效的数据处理和分析工具，为地震研究人员提供极大的便利。

一、MATLAB 在地震资料处理中的应用MATLAB 在地震资料处理中的应用非常广泛，包括地震波的模拟、滤波器的设计与实现、频谱分析、地震反应分析等。

利用 MATLAB 可以对地震数据进行预处理，如去除噪声、放大有效信号等，从而提高地震信号的质量。

此外，MATLAB 还可以对地震波形进行分析，如计算地震波的周期、振幅、频率等参数，为地震研究提供基础数据。

二、用 MATLAB 实现滤波器对数字地震资料处理滤波器是地震资料处理中的一种重要技术，可以有效地去除地震信号中的噪声，提高信号的质量。

MATLAB 提供了丰富的滤波器设计方法和算法，如低通滤波器、高通滤波器、带通滤波器等。

通过使用 MATLAB，可以方便地设计出符合要求的滤波器，并对地震信号进行滤波处理。

三、地震资料处理的并行处理方法地震资料处理往往涉及到大量的数据计算和分析，因此，提高地震资料处理的效率非常重要。

MATLAB 提供了并行计算功能，可以有效地加快地震资料处理的速度。

通过使用 MATLAB 的并行计算功能，可以实现对地震数据的并行处理，从而提高地震资料处理的效率。

四、结论总之，MATLAB 在地震资料处理中具有广泛的应用，可以提供强大的数据处理和分析功能，为地震研究人员提供极大的便利。