简单几何体及空间图形的基本关系
- 格式:docx
- 大小:367.61 KB
- 文档页数:9

第一章 空间几何体知识点归纳1、空间几何体的结构:空间几何体分为多面体和旋转体和简单组合体⑴常见的多面体有:棱柱、棱锥、棱台;常见的旋转体有:圆柱、圆锥、圆台、球。
简单组合体的构成形式:⑵棱柱:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱。
⑶棱台:用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分,这样的多面体叫做棱台。
1、空间几何体的三视图和直观图投影:中心投影 平行投影(1)定义:几何体的正视图、侧视图和俯视图统称为几何体的三视图。
(2)三视图中反应的长、宽、高的特点:“长对正”,“高平齐”,“宽相等”2、空间几何体的直观图(表示空间图形的平面图). 观察者站在某一点观察几何体,画出的图形.3、斜二测画法的基本步骤:①建立适当直角坐标系xOy (尽可能使更多的点在坐标轴上)②建立斜坐标系'''x O y ∠,使'''x O y ∠=450(或1350),注意它们确定的平面表示水平平面;③画对应图形,在已知图形平行于X 轴的线段,在直观图中画成平行于X ‘轴,且长度保持不变;在已知图形平行于Y 轴的线段,在直观图中画成平行于Y ‘轴,且长度变为原来的一半;4、空间几何体的表面积与体积⑴圆柱侧面积;l r S ⋅⋅=π2侧面⑵圆锥侧面积:l r S ⋅⋅=π侧面 ⑶圆台侧面积:()S r R l π=+侧面⑷体积公式:h S V ⋅=柱体;h S V ⋅=31锥体; ()13V h S S =+下台体上⑸球的表面积和体积:32344R V R S ππ==球球,.一般地,面积比等于相似比的平方,体积比等于相似比的立方。
第二章 点、直线、平面之间的位置关系及其论证1,,A l B ll A B ααα∈∈⎧⇒⊂⎨∈∈⎩ 公理1的作用:判断直线是否在平面内2、公理2:过不在一条直线上的三点,有且只有一个平面。


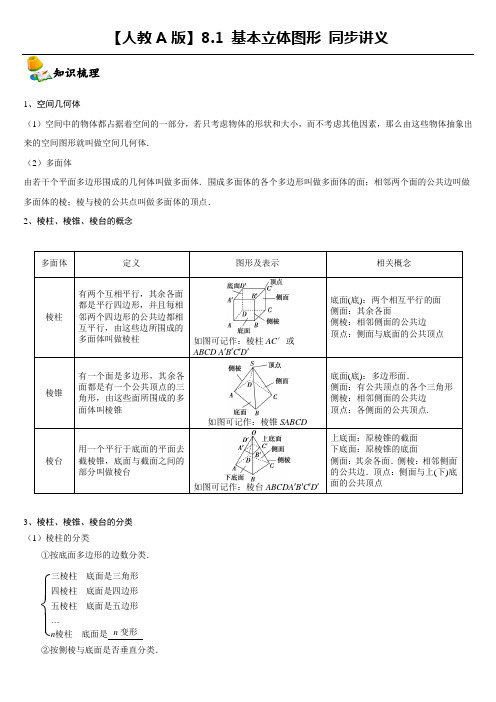
【人教A 版】8.1 基本立体图形 同步讲义1、空间几何体(1)空间中的物体都占据着空间的一部分,若只考虑物体的形状和大小,而不考虑其他因素,那么由这些物体抽象出来的空间图形就叫做空间几何体. (2)多面体由若干个平面多边形围成的几何体叫做多面体.围成多面体的各个多边形叫做多面体的面;相邻两个面的公共边叫做多面体的棱;棱与棱的公共点叫做多面体的顶点. 2、棱柱、棱锥、棱台的概念多面体定义图形及表示相关概念棱柱有两个互相平行,其余各面都是平行四边形,并且每相邻两个四边形的公共边都相互平行,由这些边所围成的多面体叫做棱柱如图可记作:棱柱AC ′或 ABCD A ′B ′C ′D ′底面(底):两个相互平行的面 侧面:其余各面侧棱:相邻侧面的公共边 顶点:侧面与底面的公共顶点棱锥有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫棱锥如图可记作:棱锥SABCD底面(底):多边形面.侧面:有公共顶点的各个三角形 侧棱:相邻侧面的公共边 顶点:各侧面的公共顶点. 棱台用一个平行于底面的平面去截棱锥,底面与截面之间的部分叫做棱台如图可记作:棱台ABCDA ′B ′C ′D ′上底面:原棱锥的截面 下底面:原棱锥的底面侧面:其余各面.侧棱:相邻侧面的公共边.顶点:侧面与上(下)底面的公共顶点3、棱柱、棱锥、棱台的分类 (1)棱柱的分类①按底面多边形的边数分类.⎩⎪⎨⎪⎧三棱柱底面是三角形四棱柱底面是四边形五棱柱底面是五边形…n 棱柱底面是②按侧棱与底面是否垂直分类.知识梳理n 变形⎩⎨⎧直棱柱⎩⎪⎨⎪⎧正棱柱其他直棱柱斜棱柱(2)棱锥的分类(棱台分类)①按底面多边形的边数分类. 三棱锥、四棱锥、五棱锥等. ②按底面多边形是否为正多边形分类. 正棱锥和一般棱锥. 4、旋转体由一个平面图形绕它所在平面内的一条定直线旋转所形成的封闭几何体叫做旋转体,这条定直线叫做旋转体的轴. 5、圆柱、圆锥、圆台的概念 旋转体结构特征图示表示法圆柱以矩形的一边所在直线为旋转轴,其余三边旋转形成的面所围成的旋转体叫做圆柱.旋转轴叫做圆柱的轴;垂直于轴的边旋转而成的圆面叫做圆柱的底面;无论旋转到什么位置,不垂直于轴边都叫做圆柱侧面的母线。

4空间图形的基本关系与公理【教学目标】1.理解空间中点、线、面的位置关系;2.理解空间中平行直线、相交直线、异面直线、平行平面、相交平面等概念;3.掌握三个公理及推论,并能运用它们去解决有关问题;4.会用集合语言来描述点、直线和平面之间的关系以及图形的性质.【重点难点】掌握三个公理及推论,并能运用它们去解决有关问题【教法教具】以讲学稿为依托的探究式教学方法,多媒体教学【教学课时】 2课时【教学流程】自主学习(课前完成,含独学和质疑)1.空间点与直线的位置关系(1)如果点P在直线a,记作P∈a.(2)如果点P在直线a,记作P∉a.2.空间点与平面的位置关系(1)如果点P在平面α,记作P∈α.(2)如果点P在平面α,记作P∉α.3.空间两条直线的位置关系(1)平行直线:如果直线a和b在同一个平面内,但没有,这样的两条直线叫作平行直线,记作a∥b.(2)相交直线:如果直线a和b有且只有公共点P,这样的两条直线叫作相交直线,记作a∩b=P.(3)异面直线:如果直线a和b不同在平面内,这样的两条直线叫作异面直线.4.空间直线与平面的位置关系(1)直线在平面内:如果直线a与平面α有个公共点,我们称直线a在平面α内,记作aα.(2)直线与平面相交:如果直线a与平面α有且只有公共点P,我们称直线a与平面α相交于点P,记作a∩α=P.(3)直线与平面平行:如果直线a与平面α没有,我们称直线a与平面α平行,记作a∥α.5.空间平面与平面的位置关系(1)平行平面:如果平面α与平面β没有,我们称平面α与平面β是平行平面,记作α∥β.(2)相交平面:如果平面α和平面β不重合,但有,我们称平面α与平面β相交于直线l,记作α∩β=l.6.公理1如果一条直线上的在一个平面内,那么这条直线上所有的点都在这个平面内(即直线在平面内).7.公理2经过的三点,有且只有一个平面.或简单说成:不共线的三点确定一个平面.8.公理3如果两个的平面有一个公共点,那么它们有且只有一条通过这个点的公共直线.9.公理2的推论推论1:经过一条直线和这条,有且只有一个平面;推论2:经过两条直线,有且只有一个平面;推论3:经过两条直线,有且只有一个平面.合作探究:(对学、群学)探究点一空间点、线、面的位置关系导引观察下面三个长方体回答下列问题.思考 1 观察长方体,你能发现长方体有多少个顶点?多少条棱?多少个面?棱所在的直线,以及侧面、底面之间的位置关系吗?例1 将下面用符号语言表示的关系用文字语言予以叙述,并用图形语言予以表示:α∩β=l,A∈l,ABα,ACβ.跟踪训练1 根据下列符号表示的语句,说明点、线、面之间的位置关系,并画出相应的图形:(1)A∈α,B∉α;(2)lα,m∩α=A,A∉l;(3)P∈l,P∉α;Q∈l,Q∈α.探究点二空间图形的公理思考1 实际生活中,我们有这样的经验:把一根直尺边缘上的任意两点放到桌面上,可以看到,直尺的整个边缘就落在了桌面上.从经验中我们能得到什么结论呢?思考2 如何用符号语言表示公理1?公理1有怎样的用途?思考3 生活中经常看到用三角架支撑照相机;测量员用三角架支撑测量用的平板仪;有的自行车后轮旁只安装一只撑脚.上述事实和类似经验可以归纳出平面怎样的性质?思考4 如何用符号语言表示公理2?公理2有怎样的用途?思考5 如图所示,直线BC外一点A和直线BC能确定一个平面吗?为什么?思考6 如图所示,两条相交直线能不能确定一个平面?为什么?思考7 如图所示,两条平行直线能不能确定一个平面?为什么?思考8 我们已经看到各种棱柱、棱锥的每两个相交的面之间的交线都是直线段,由此你能总结出怎样的结论?思考9 如何用符号语言表示公理3?公理3有怎样的用途?例2 已知a∥b∥c,l∩a=A,l∩b=B,l∩c=C.求证:a,b,c和l共面.跟踪训练2 已知:如图所示,l1∩l2=A,l2∩l3=B,l1∩l3=C.求证:直线l1、l2、l3在同一平面内.探究点三共线问题例3 已知△ABC在平面α外,AB∩α=P,AC∩α=R,BC∩α=Q,如图所示.求证:P、Q、R三点共线.跟踪训练3 如图所示,在正方体ABCD—A1B1C1D1中,E为AB的中点,F为AA1的中点.求证:CE、D1F、DA三线交于一点.【达标拓展】(检测、拓展)1.若A∈平面α,B∈平面α,C∈直线AB,则( )A.C∈αB.C αC.ABαD.AB∩α=C2.平行六面体ABCD—A1B1C1D1中,既与AB共面也与CC1共面的棱的条数为( )A.3 B.4 C.5 D.63.若三个平面两两相交,且三条交线互相平行,则这三个平面把空间分成________部分.4.如图,已知D,E是△ABC的边AC,BC上的点,平面α经过D,E两点,若直线AB与平面α的交点是P,则点P与直线DE的位置关系是________.【学后反思】【练案】一、基础过关1.下列图形中,不一定是平面图形的是( )A.三角形B.菱形C.梯形D.四边相等的四边形2.空间中,可以确定一个平面的条件是( )A.两条直线B.一点和一条直线C.一个三角形 D.三个点3.如图所示,用符号语言可表示为( )A.α∩β=m,nα,m∩n=AB.α∩β=m,n∈α,m∩n=AC.α∩β=m,nα,A m,A nD.α∩β=m,n∈α,A∈m,A∈n4.已知平面α与平面β、γ都相交,则这三个平面可能的交线有( ) A.1条或2条B.2条或3条C.1条或3条 D.1条或2条或3条5.给出以下命题:①和一条直线都相交的两条直线在同一平面内;②三条两两相交的直线在同一平面内;③有三个不同公共点的两个平面重合;④两两平行的三条直线确定三个平面.其中正确命题的个数是________.6.已知α∩β=m,aα,bβ,a∩b=A,则直线m与A的位置关系用集合符号表示为________.7.如图,梯形ABDC中,AB∥CD,AB>CD,S是直角梯形ABDC所在平面外一点,画出平面SBD和平面SAC的交线,并说明理由.二、能力提升8.空间不共线的四点,可以确定平面的个数是( )A.0B.1C.1或4D.无法确定9.空间中A,B,C,D,E五个点,已知A,B,C,D在同一平面内,B,D,C,E在同一平面内,那么这五点( )A.共面B.不一定共面C.不共面D.以上都不对10.已知α、β为平面,A、B、M、N为点,a为直线,下列推理错误的是________.①A∈a,A∈β,B∈a,B∈β⇒aβ;②M∈α,M∈β,N∈α,N∈β⇒α∩β=MN;③A∈α,A∈β⇒α∩β=A;④A、B、M∈α,A、B、M∈β,且A、B、M不共线⇒α、β重合.11.如图,在长方体ABCD-A1B1C1D1中,O1是A1C1与B1D1的交点,长方体体对角线A1C交截面AB1D1于点P.求证:O1,P,A三点在同一条直线上.12.已知a,b,c,d是两两相交且不共点的四条直线,求证:a,b,c,d共面.三、探究与拓展13.在四面体ABCD中,E,G分别为BC,AB的中点,F在CD上,H在AD上,且有DF∶FC=DH∶HA=2∶3.求证:EF,GH,BD交于一点.。

《空间图形的基本关系》教学设计说明本节选自普通高中北师大版必修2第一章第四节第一课时【教材分析】空间图形的基本关系与公理是学习平行关系与垂直关系的基础。
教材依托长方体,表述了空间点、线、面间的基本位置关系。
教材先引导学生对“实例分析”中的长方体进行仔细的观察,然后讨论长方体的顶点、棱、面之间的关系。
在此基础上,在进入“抽象概括”,总结出空间点、线、面的五类位置关系。
这样处理的目的是让学生通过长方体这个具体模型对位置关系有直观地认识。
注意三种语言即文字语言、符号语言、图形语言的互译,让学生熟练掌握点、线、面的符号表示,及“∈”和“≠⊂”符号的正确使用。
【三维目标】1.知识与技能(1)了解构成空间图形的基本元素:点、直线、平面。
(2)借助长方体模型,在直观认识和理解空间点、线、面的位置关系的基础上抽象出点、线、面的位置关系的定义。
(3)正确使用用图形语言、符号语言进行表述点、线、面的位置关系。
2.过程与方法学生在“立体几何初步”起始课中从对空间几何体的整体观察入手,遵循从整体到局部,从具体到抽象的原则,认识空间中点、线、面之间的位置关系。
3.情感、态度与价值观通过对空间图形的认识,使学生知道我们生活的三维空间是丰富多彩的,结合三种语言的互相转换,体会数学图形的直观美以及数学语言的简洁美。
【重点分析】本节课的重点是在以长方体为载体,直观认识和理解空间点、线、面的位置关系的基础上进一步培养学生符号语言的运用能力。
在立体几何初步的教学中,长方体是一个重要模型,在教学中应特别重视长方体这一模型的应用,通过长方体让学生在直观感知的基础上认识空间中一般点、线、面之间的位置关系。
本节课进一步对一些关系用符号语言进行表述,旨在培养学生符号语言的运用能力。
在本节课中,要突出长方体的重要作用,注重引导学生利用长方体模型理解空间中点、线、面的位置关系,实现立体几何中由具体到抽象、由直观感知到抽象概括的目标。
【难点分析】本节课的难点是对异面直线的理解,对于本节课的难点,由导学案上思考交流问题的设计,以及教师的逐步引导,让学生能够很好的突破本节课的难点。
《几何图形初步》全章知识讲解【学习目标】1.认识一些简单的几何体的平面展开图及三视图,初步培养空间观念和几何直观; 2.掌握直线、射线、线段、角这些基本图形的概念、性质、表示方法和画法; 3.初步学会应用图形与几何的知识解释生活中的现象及解决简单的实际问题;4.逐步掌握学过的几何图形的表示方法,能根据语句画出相应的图形,会用语句描述简单的图形. 【要点梳理】要点一、多姿多彩的图形 1. 几何图形的分类要点诠释:在给几何体分类时,不同的分类标准有不同的分类结果. 2.立体图形与平面图形的相互转化 (1)立体图形的平面展开图:把立体图形按一定的方式展开就会得到平面图形,把平面图形按一定的途径进行折叠就会得到相应的立体图形,通过展开与折叠能把立体图形和平面图形有机地结合起来. 要点诠释:①对一些常见立体图形的展开图要非常熟悉,例如正方体的 11种展开图,三棱柱,圆柱等的展开图;②不同的几何体展成不同的平面图形,同一几何体沿不同的棱剪开,可得到不同的平面图形,那么排除障碍的方法就是:联系实物,展开想象,建立“模型”,整体构想,动手实践. (2)从不同方向看:立体图形:棱柱、棱锥、圆柱、圆锥、球等. ⎧⎨⎩平面图形:三角形、四边形、圆等.几何图形⎧⎨⎩主(正)视图----------从正面看几何体的三视图左视图----------------从左边看俯视图----------------从上面看要点诠释:①会判断简单物体(直棱柱、圆柱、圆锥、球)的三视图.②能根据三视图描述基本几何体或实物原型.(3)几何体的构成元素及关系几何体是由点、线、面构成的.点动成线,线与线相交成点;线动成面,面与面相交成线;面动成体,体是由面组成.要点二、直线、射线、线段1.直线,射线与线段的区别与联系2. 基本性质(1)直线的性质:两点确定一条直线.(2)线段的性质:两点之间,线段最短.要点诠释:①本知识点可用来解释很多生活中的现象. 如:要在墙上固定一个木条,只要两个钉子就可以了,因为如果把木条看作一条直线,那么两点可确定一条直线。