结构动力学(2)

====Word 行业资料分享--可编辑版本--双击可删====第一章 单自由度系统1.1 总结求单自由度系统固有频率的方法和步骤。

单自由度系统固有频率求法有：牛顿第二定律法、动量距定理法、拉格朗日方程法和能量守恒定理法。

1、 牛顿第二定律法适用范围：所有的单自由度系统的振动。

解题步骤：（1） 对系统进行受力分析,得到系统所受的合力；（2） 利用牛顿第二定律∑=F x m,得到系统的运动微分方程；（3） 求解该方程所对应的特征方程的特征根，得到该系统的固有频率。

2、 动量距定理法适用范围：绕定轴转动的单自由度系统的振动。

解题步骤：（1） 对系统进行受力分析和动量距分析；（2） 利用动量距定理J ∑=M θ,得到系统的运动微分方程；（3） 求解该方程所对应的特征方程的特征根，得到该系统的固有频率。

3、 拉格朗日方程法：适用范围：所有的单自由度系统的振动。

解题步骤：（1）设系统的广义坐标为θ，写出系统对于坐标θ的动能T 和势能U 的表达式；进一步写求出拉格朗日函数的表达式：L=T-U ； （2）由格朗日方程θθ∂∂-∂∂∂LL dt )( =0，得到系统的运动微分方程； （3） 求解该方程所对应的特征方程的特征根，得到该系统的固有频率。

4、 能量守恒定理法适用范围：所有无阻尼的单自由度保守系统的振动。

解题步骤：（1）对系统进行运动分析、选广义坐标、写出在该坐标下系统的动能T 和势能U 的表达式；进一步写出机械能守恒定理的表达式 T+U=Const（2）将能量守恒定理T+U=Const 对时间求导得零,即0)(=+dtU T d ，进一步得到系统的运动微分方程；（3） 求解该方程所对应的特征方程的特征根，得到该系统的固有频率。

1.2 叙述用衰减法求单自由度系统阻尼比的方法和步骤。

用衰减法求单自由度系统阻尼比的方法有两个：衰减曲线法和共振法。

方法一：衰减曲线法。

求解步骤：（1）利用试验测得单自由度系统的衰减振动曲线，并测得周期和相邻波峰和波谷的幅值i A 、1+i A 。

结构动力学问答题答案-武汉理工-研究生《结构动力学》思考题第1章1、对于任一振动系统，可划分为由激励、系统和响应三部分组成。

试结合生活或工程分别举例说明：何为响应求解、环境识别和系统识别？响应求解：结构系统和荷载已知，求响应。

又称响应预估问题，是工程正问题的一种，通常在工程中是指结构系统已知，具体指结构的形状构件及离散元件等，环境识别：主要是荷载的识别，结构和响应已知，求荷载。

属于工程反问题的一种。

在工程中，如已知桥梁的结构和响应，根据这些来反推出桥梁所受到的荷载。

系统识别：荷载和响应已知，求结构的参数或数学模型。

又称为参数识别，是工程反问题的一种，在土木工程领域，房屋、桥梁和大坝等工程结构被视为“系统”，而“识别”意味着由振动实验数据求得结构的动力特性（如频率、阻尼比和振型）。

如模态分析和模态试验技术等基本成型并得到广泛应用。

2、如何从物理意义上理解线性振动系统 解的可叠加性。

求补充！！！！！3、正确理解等效刚度的概念，并求解单自由度系统的固有频率。

复杂系统中存在多个弹性元件时，用等效弹性元件来代替原来所有的弹性元件，等效原则是等效元件刚度等于组合元件刚度，则等效元件的刚度称为等效刚度。

4、正确理解固有频率f 和圆频率ω的物理意义。

固有频率f ：物体做自由振动时，振动的频率与初始条件无关，而仅与系统的本身的参数有关(如质量、形状、材质等)，它是自由振动周期的倒数，表示单位时间内振动的次数。

圆频率ω： ω=2π/T=2πf 。

即为单位时间内位移矢量在复平面内转动的弧度，又叫做角频率。

它只与系统本身的参数m ，k 有关，而与初始条件无关5、正确理解过阻尼、临界阻尼、欠阻尼的概念。

一个系统受初扰动后不再受外界激励，因为受到阻力造成能量损失而位移峰值渐减的振动称为阻尼振动。

系统的状态按照阻尼比ζ来划分。

把ζ=0的情况称为无阻尼，即周期运动;把0<ζ<1的情况称为欠阻尼，即系统所受的阻尼力较小，振幅在逐渐减小，最后才达到平衡位置;把ζ>1的情况称为过阻尼，如果阻尼再增大，系统需要较长的时间才能达到平衡;把ζ=1的情况称为临界阻尼，即阻尼的大小刚好使系统作非"周期"运动。

结构动力学思考题made by 云屹思考题一1、结构动力学与静力学的主要区别是什么？结构的运动方程有什么不同？主要区别为：(1)动力学考虑惯性力的影响，静力学不考虑惯性力的影响；(2)动力学中位移等量与时间有关，静力学中位移等量不随时间变化；(3)动力学的求解方法通常与荷载类型有关，静力学一般无关。

运动方程的不同：动力学的运动方程包括位移项、速度项和加速度项；静力学的平衡方程只包括位移项。

2、什么是动力自由度？什么是静力自由度？区分动力自由度和静力自由度的意义是什么？动力自由度：确定结构体系质量位置的独立参数；静力自由度：确定结构体系在空间中的几何位置的独立参数。

意义：通过适当的假设，当静力自由度数大于动力自由度数时，使用动力自由度可以减少未知量，简化计算，提高计算效率。

3、采用集中质量法、广义坐标法和有限元法都可以使无限自由度体系简化为有限自由度体系，它们所采用的手法有什么不同？4、在结构振动的过程中引起阻尼的原因有哪些？(1)材料的摩擦或材料变形引起的热耗散；(2)构件连接处或结构构件与非结构构件之间的摩擦；(3)结构外部介质的阻尼。

5、在建立结构运动方程时，如考虑重力的影响，动位移的运动方程有无改变？如果满足条件：(1)线性问题；(2)重力的影响预先被平衡；则动位移的运动方程不会改变，否则会改变。

思考题二1、刚度系数k ij和质量系数m ij的直接物理意义是什么？如何直接用m ij的物理概念建立梁单元的质量矩阵[M]？k ij：由第j自由度的单位位移所引起的第i自由度的力；m ij：由第j自由度的单位加速度所引起的第i自由度的力。

依次令第j（j=1,2,3,4）自由度产生单位加速度，而其他的广义坐标处保持静止，使用平衡方程解出第i自由度上的力，从而得到m ij，集成得到质量矩阵[M]。

2、如何用刚度矩阵和质量矩阵，以矩阵的形式表示多自由度体系的势能和动能？{}[]{}1=2TT u M u {}[]{}1=2TV u K u3、建立多自由度体系运动方程的直接动力平衡法和拉格朗日方程法的优缺点是什么？ (1)直接动力平衡法：优点：概念直观，易于通过各个结构单元矩阵建立整体矩阵，便于计算机编程。

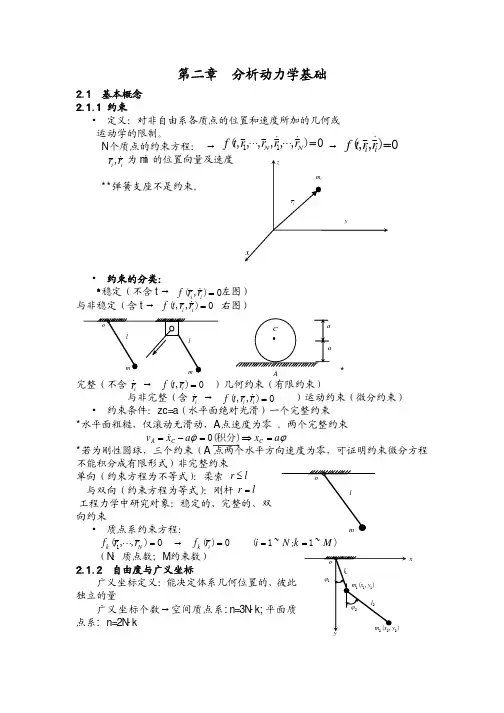
第二章 分析动力学基础2.1 基本概念 2.1.1 约束• 定义：对非自由系各质点的位置和速度所加的几何或 运动学的限制。

N 个质点的约束方程： → → 为mi 的位置向量及速度 **弹簧支座不是约束。

• 约束的分类：*稳定（不含t → 左图） 与非稳定（含t → 右图）* 完整（不含 → ）几何约束（有限约束） 与非完整（含 → ）运动约束（微分约束） • 约束条件：zc=a （水平面绝对光滑）一个完整约束 *水平面粗糙，仅滚动无滑动，A 点速度为零 。

两个完整约束*若为刚性圆球，三个约束（A点两个水平方向速度为零，可证明约束微分方程不能积分成有限形式）非完整约束单向（约束方程为不等式）：柔索 与双向（约束方程为等式）：刚杆 工程力学中研究对象：稳定的、完整的、双 向约束• 质点系约束方程：→ （N ：质点数；M 约束数） 2.1.2 自由度与广义坐标 广义坐标定义：能决定体系几何位置的、彼此独立的量广义坐标个数→空间质点系:n=3N-k;平面质点系: n=2N-k0),,,,,,(11=⋅⋅⋅⋅⋅⋅N N r r r r t f 0),,(=i i r r t f i i r r ,0),(=i i rr f 0),,(=i i rr t f Ai r0),(=i r t f i r 0),,(=i i rr t f ϕϕa x a x v C C A =⇒=−=)(0积分 lr ≤l r =0),,(1=⋅⋅⋅N k r r f )~1;~1(0)(M k N i r f i k ===x双连刚杆双质点系的约束方程：广义坐标数：广义坐标：独立参数→角度→ 振型等（见下页） 梁的挠度曲线用三角级数表示： 广义坐标→*自由度定义：在固定时刻，约束许可条件下能自由变更的 独立的坐标数目（对完整约束=广义坐标数）• 自由度数→空间质点系：n=3N-k 平面质点系：n=2N-k （N ：质点数；k: 约束数） 非完整约束：（广义坐标数>系统自由度数）2.1.3 功的定义元功：A →B 过程中力作的功：对摩擦传动轮的例，由于力未移动，位移=？ • 功的新定义：(传动齿轮)• 功率：2.1.4 有势力和体系的势能有势力：（1）大小和方向只决定于体系质点的位置（2）体系从位置A 移动到位置B ，力作功只决定于位置而与路径无关取体系的任意位置为“零位置O ”，从位置A 移动到零位置O 各力作的功为体系在位置A 时的势能UA(位能)。

结构力学(Ⅱ)教案一、引言课程介绍：本课程是结构力学的高级课程，旨在加深学生对结构力学的基本概念、原理和方法的理解，掌握复杂结构体系的受力分析与设计方法。

目标：通过本章的学习，学生应能够理解并应用结构力学的原理，对复杂结构进行受力分析，并确定结构的稳定性与承载能力。

二、平面力系内容：平面力系的合成与分解，力的平衡条件，力矩与力偶矩，平面力系的平衡方程。

目标：学生应能够进行平面力系的合成与分解，应用平衡条件解决力矩问题，并利用平衡方程求解复杂力系的平衡。

三、空间力系内容：空间力系的合成与分解，空间力系的平衡条件，空间力矩与力偶矩，空间力系的平衡方程，自由度的概念。

目标：学生应能够进行空间力系的合成与分解，解决空间力矩问题，利用平衡方程求解复杂空间力系的平衡，并理解结构体系中自由度的概念。

四、轴向力与剪力内容：轴向力的概念，剪力的概念，轴向力与剪力的计算，剪力图的绘制。

目标：学生应能够理解轴向力和剪力的概念，计算简单结构中的轴向力和剪力，并绘制剪力图以分析结构的受力情况。

五、弯曲力与弯矩内容：弯曲力的概念，弯矩的概念，弯曲力与弯矩的计算，弯矩图的绘制。

目标：学生应能够理解弯曲力和弯矩的概念，计算简单结构中的弯曲力和弯矩，并绘制弯矩图以分析结构的受力情况。

六、扭转内容：扭转的概念，扭转力矩的概念，扭转力矩的计算，扭转剪切应力与扭转应变，扭转弹性稳定性的概念。

目标：学生应能够理解扭转的概念和扭转力矩的概念，计算简单杆件的扭转力矩，分析扭转剪切应力和扭转应变，理解扭转弹性稳定性的概念。

七、剪力墙与框架结构内容：剪力墙的概念和特点，框架结构的概念和特点，剪力墙和框架结构的受力分析，剪力墙和框架结构的承载力计算。

目标：学生应能够理解剪力墙和框架结构的概念和特点，进行剪力墙和框架结构的受力分析，计算剪力墙和框架结构的承载力。

八、空间结构内容：空间结构的概念，空间结构的受力分析，空间结构的承载力计算，空间结构的设计方法。