2.2结构动力学知识点讲解

讲义总结注册结构专业基础结构动力特性及动力反应讲义.doc 讲义总结：注册结构专业基础结构动力特性及动力反应一、引言结构动力特性和动力反应是结构工程中的重要概念，它们对于评估和设计能够抵抗动态荷载（如地震、风荷载等）的结构至关重要。

本讲义旨在总结结构动力特性的基础理论和动力反应的计算方法。

二、结构动力特性自振频率：结构在无阻尼自由振动下的固有频率，是动力特性的重要参数。

阻尼比：结构振动时能量耗散的程度，影响结构的动力反应。

模态：结构在振动中的运动形态，每个模态对应一个自振频率。

三、动力反应分析静力法：假设结构在动态荷载下的反应与静态荷载下相同，适用于低阻尼结构。

反应谱法：利用地震反应谱来估计结构在地震作用下的反应。

时程分析法：考虑地震波形的详细时间历程，对结构进行动力反应分析。

模态分析：将结构的复杂振动分解为若干个主要模态的组合。

四、动力反应的影响因素结构类型：不同类型的结构（如框架、剪力墙、框筒等）具有不同的动力特性。

材料特性：结构材料的弹性模量、密度和阻尼比等影响动力反应。

边界条件：固定支撑、弹性支撑等不同的边界条件对动力反应有显著影响。

荷载特性：荷载的大小、方向和作用方式（如冲击、周期性等）。

五、抗震设计原则延性设计：设计结构以具有足够的塑性变形能力，以消耗输入能量。

能量耗散：通过设置耗能装置，如阻尼器，来减少结构的动力反应。

多道防线：设计多个抗震防线，以确保结构在严重地震下仍能保持整体稳定。

六、案例分析某框架结构抗震设计：通过合理选择结构布局和材料，以及设置耗能支撑，提高了结构的抗震性能。

某高层建筑动力反应分析：采用时程分析法，考虑了多种地震波形，评估了建筑在不同地震作用下的反应。

七、存在问题与挑战非线性分析：结构在强震下的非线性行为对分析和设计提出了更高要求。

不确定性：地震荷载的不确定性要求设计中考虑足够的安全系数。

高性能计算：随着计算能力的提升，更复杂的动力反应分析方法成为可能。

八、未来展望随着科技进步和新材料的开发，结构动力特性的研究和动力反应的预测将更加精确。

结构动力学 动力特性（天生就有的，爹妈给的，不随外界任何事物改变）自振频率ω：初速度或初位移引起自由振动的圆频率振型：结构按照某自振频率振动的位移形态阻尼：振动过程中的能量耗散（主要由结构内部的特征决定的）动力作用：周期荷载、冲击荷载、随机荷载（地震）动力反应（响应）：动内力、动荷载、速度、加速度结构动力学是研究动力反应的规律的学问，一般思路是先研究自由振动（目的是搞清该结构的动力特性）再研究强迫振动（动力特性+动力作用）利用振型分解反应谱法，可以将每个基本振型的参与系数求出来，这样的最大好处是可以将耦联微分方程解耦。

刚度法通式：()()()()mY t cY t kY t F t ++=1、 单自由度无阻尼自由振动（分析自由振动的目的是确定体系的动力特性：周期、自振频率）()()0my t ky t += （()[()]y t my t δ=-） （令k m ω=） 解为：00()cos sin v y t y t t ωωω=+=sin()A t ωϕ+ （22002v A y ω=+，00tan y v ωϕ=） 重要结论：由微分方程的解可以知道，无阻尼振动是一个简谐振动，其周期和自振频率为2T πω=，k mω=周期和自振频率之和自己质量与刚度有关和外界因素无关。

2、单自由度有阻尼自由振动()()()0my t cy t ky t ++= （令=22c c mw mkξ=） 即微分方程为2()2()()0y t wy t w y t ξ++=（实际建筑结构的阻尼比1ξ<）解为000()[sin cos ]t d d dv y y t e t y t ξωξωωωω-+=+=sin()t d Ae t ξωωϕ-+（21d ωωξ=-） 221000000(),d d v y y A y tg v y ξωωϕωξω-+=+=+其中 重要结论：1）由方程的解看出弱阻尼情况下的自由振动是一种衰减振动，阻尼使振幅按指数规律衰减。

前言结构动力学是比较难学的一门课程，但是你一旦学会并且融会贯通，你就会为成为结构院士、大师和总工垫定坚实的基础。

结构动力学学习的难点主要有以下两个方面。

1 概念难理解，主要表现在两个方面，一是表达清楚难，如果你对概念理解的很透彻，那么你写的书对概念的表述也会言简意赅，切中要害（克里夫的书就是这个特点），有的书会对一个概念用了很多文字进行解释，但是还是没有说清楚，也有的书受水平限制，本身表述就不清楚。

二是理解难，有点只可意会不可言传的味道，老师讲的头头是道，自己听得云山雾绕。

2 公式推导过程难，一是力学知识点密集，推导过程需要力学概念清析，并且需要每一步的力学公式熟悉；二是需要一定的数学基础，而且有的是在本科阶段并没有学习的数学知识。

克里夫《结构动力学》被称为经典的结构动力学教材，但是也很难看懂。

之所以被称为经典，主要就是对力学的概念表达的语言准确，概念清楚。

为什么难懂呢？是因为公式的推导过程比较简单，省略过多。

本来公式的推导过程既需要力学概念清楚也需要数学公式熟悉，但是一般人不是力学概念不清楚，就是数学公式不熟悉，更有两者都不熟悉者。

所以在学习过程中感觉很难，本学习详解是在该书概念清楚的基础上，对力学公式推导过程进行详细推导，并且有的加以解释，帮助你在学习过程中加深理解和记忆。

达到融会贯通，为你成为结构院士、大师和总工垫定坚实的基础。

以下黑体字是注释，其它为原书文字。

[美] R∙克里夫《结构动力学》辅导学习详解第1章结构动力学概述… …第Ⅰ篇单自由度体系第2章基本动力体系的组成… …§2-5 无阻尼自由振动分析如上一节所述，有阻尼的弹簧-质量体系的运动方程可表示为mv̈(t)+cv̇(t)+kν(t)=p(t)（2-19）其中ν(t)是相对于静力平衡位置的动力反应；p(t)是作用于体系的等效荷载，它可以是直接作用的或是支撑运动的结构。

为了获得方程（2-19）的解，首先考虑方程右边等于零的齐次方程，即mv̈(t)+cv̇(t)+kν(t)=0（2-20）mv(t)+kν(t)=0（2-20a）此处公式应该为mv(t)+kν(t)=0，因为该节是无阻尼自由振，而且（2-20）的解，式（2-21）也是公式mv(t)+kν(t)=0的解在作用力等于零时产生的运动称为自由振动，现在要研究的即为体系的自由振动反应。

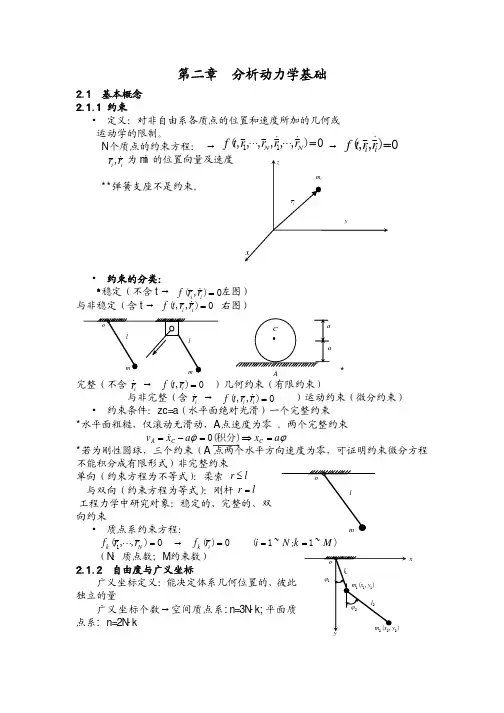
第二章 分析动力学基础2.1 基本概念 2.1.1 约束• 定义：对非自由系各质点的位置和速度所加的几何或 运动学的限制。

N 个质点的约束方程： → → 为mi 的位置向量及速度 **弹簧支座不是约束。

• 约束的分类：*稳定（不含t → 左图） 与非稳定（含t → 右图）* 完整（不含 → ）几何约束（有限约束） 与非完整（含 → ）运动约束（微分约束） • 约束条件：zc=a （水平面绝对光滑）一个完整约束 *水平面粗糙，仅滚动无滑动，A 点速度为零 。

两个完整约束*若为刚性圆球，三个约束（A点两个水平方向速度为零，可证明约束微分方程不能积分成有限形式）非完整约束单向（约束方程为不等式）：柔索 与双向（约束方程为等式）：刚杆 工程力学中研究对象：稳定的、完整的、双 向约束• 质点系约束方程：→ （N ：质点数；M 约束数） 2.1.2 自由度与广义坐标 广义坐标定义：能决定体系几何位置的、彼此独立的量广义坐标个数→空间质点系:n=3N-k;平面质点系: n=2N-k0),,,,,,(11=⋅⋅⋅⋅⋅⋅N N r r r r t f 0),,(=i i r r t f i i r r ,0),(=i i rr f 0),,(=i i rr t f Ai r0),(=i r t f i r 0),,(=i i rr t f ϕϕa x a x v C C A =⇒=−=)(0积分 lr ≤l r =0),,(1=⋅⋅⋅N k r r f )~1;~1(0)(M k N i r f i k ===x双连刚杆双质点系的约束方程：广义坐标数：广义坐标：独立参数→角度→ 振型等（见下页） 梁的挠度曲线用三角级数表示： 广义坐标→*自由度定义：在固定时刻，约束许可条件下能自由变更的 独立的坐标数目（对完整约束=广义坐标数）• 自由度数→空间质点系：n=3N-k 平面质点系：n=2N-k （N ：质点数；k: 约束数） 非完整约束：（广义坐标数>系统自由度数）2.1.3 功的定义元功：A →B 过程中力作的功：对摩擦传动轮的例，由于力未移动，位移=？ • 功的新定义：(传动齿轮)• 功率：2.1.4 有势力和体系的势能有势力：（1）大小和方向只决定于体系质点的位置（2）体系从位置A 移动到位置B ，力作功只决定于位置而与路径无关取体系的任意位置为“零位置O ”，从位置A 移动到零位置O 各力作的功为体系在位置A 时的势能UA(位能)。

动力学基础知识梳理动力学是物理学中研究物体运动规律的领域，它主要关注物体受力和速度、加速度等因素之间的相互关系。

本文将对动力学的基础知识进行梳理，帮助读者更好地理解这一重要物理学分支。

一、力的概念和力的作用力是动力学的基础概念之一，定义为使物体发生变化（比如加速度、形状改变等）的原因。

力的作用可以描述为三个要素：力的大小、方向和作用点。

1.1 力的大小力的大小通常用牛顿（N）作为单位。

力的大小可以通过测量物体的质量和加速度来计算。

牛顿第二定律指出，力等于质量乘以加速度：F = m ×a。

其中，F表示力，m表示物体的质量，a表示物体的加速度。

1.2 力的方向力的方向是力所施加的物体的运动方向。

对于力的方向，我们常常采用坐标系，将力的方向与坐标轴建立关联。

1.3 力的作用点力的作用点是指力所施加的物体上的一个特定点。

在力同时作用于物体的多个点时，物体上不同点受到的力有可能不同。

二、牛顿三定律牛顿三定律是动力学中的重要法则，它描述了力与物体运动之间的关系。

2.1 第一定律：惯性定律牛顿第一定律也称作惯性定律，它表明物体在没有受到外力作用时将保持静止或匀速直线运动的状态。

若物体受到外力，则它将发生加速度变化。

2.2 第二定律：动量定律牛顿第二定律也称作动量定律，它给出了力、质量和加速度之间的关系。

根据牛顿第二定律，力等于质量乘以加速度：F = m × a。

2.3 第三定律：作用-反作用定律牛顿第三定律也称作作用-反作用定律，它指出对于任何一对相互作用的物体，它们之间的作用力与反作用力的大小相等、方向相反，并且作用在不同的物体上。

三、动力学中的其他重要概念除了力和牛顿三定律，动力学中还有其他一些重要概念需要掌握。

3.1 弹性碰撞弹性碰撞是指碰撞过程中物体之间能量守恒的现象。

在弹性碰撞中，物体之间的动能和动量都能够得到保持。

3.2 动能和势能动能是物体由于其运动而具有的能量，它与物体的质量和速度有关。