zf(x,y)
n
Vl i0m k 1f(k,k)k
f(k,k)
(k ,k ) k
机动 目录 上页 下页 返回 结束
2. 平面薄片的质量
有一个平面薄片, 在 xoy 平面上占有区域 D , 其面密
度为(x,y) C,计算该薄片的质量 M .
若 (x,y)(常)数 ,设D 的面积为 , 则
M
若 (x,y)非常数 , 仍可用
o
x
f(x,y)df(x,y)dxdy
D
D
问题:根据二重积 几分 何的 意义
1x2 y2dxdy
D:x2y21
机动 目录 上页 下页 返回 结束
三、二重积分的性质
1 .D kf(x,y)d kD f(x ,y)d ( k 为常数)
2 .D [ f( x ,y ) g ( x ,y )d ]
人大版微积分第三版课件87
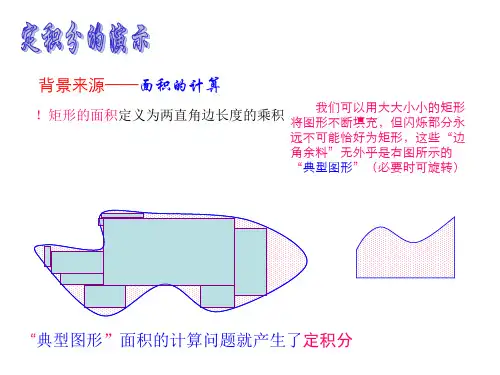
回忆定积分概念 :求曲边梯形面积步骤
1) 大化小. 在区间 [a , b] 中任意插入 n –1 个分点 a x 0 x 1 x 2 x n 1 x n b
用直线 x xi将曲边梯形分成 n 个小曲边梯形;
2) 常代变. 在第i 个窄曲边梯形上任取i[xi1,xi]
任 意 的 .
(2 )当 f(x ,y )在 闭 区 域 上 连 续 时 , 定 义 中 和 式
的 极 限 必 存 在 , 即 二 重 积 分 必 存 在 .
二重积分的几何意义 当被积函数大于零时,二重积分是柱体的体积. 当被积函数小于零时,二重积分是柱体的体积的 负值.
机动 目录 上页 下页 返回 结束
作以[xi1, xi]为底 , f (i )
y
为高的小矩形, 并以此小