当前位置：文档之家 › 第3章 逻辑代数基础-习题答案

第3章 逻辑代数基础-习题答案

  • 格式：pdf
  • 大小：88.94 KB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

逻辑代数基础习题

逻辑代数基础习题

《逻辑代数基础》练习题及答案[1.1]将下列二进制数转为等值的十六进制数的等值的十进制数。

（1）(10010111)2 ；（2）(1101101)2 ；（3）(0.01011111)2 ；（4）(11.001)2 。

[解]（1）(10010111)2 = (97)16 = (151)10，（2）(11011101)2 = (6D)16 = (109)10（3）(0.01011111)2 = (0.5F)16 = (0.37109375)10，（4）(11.001)2 = (3.2)16 = (3.125)10[1.2]将下列十六进制数化为等值的二进制数和等值的十进制数。

（1）(8C)16 ；（2）(3D.BE)16；（3）(8F.FF)16 ；（4）(10.00)16[解]（1）(8C)16 = (10001100)2 = (140)10（2）(3D·BE)16 = (111101.1011111)2 = (61.7421875)10（3）(8F·FF)16 = (10001111.11111111)2 = (143.99609375)10（4）(10.00)16 = (10000.00000000)2 = (16.00000000)10[1.3]将下列十进制数转换成等效的二进制数和等效的十进制数。

要求二进制数保留小数点以后4位有效数字。

（1）(17)10 ；（2）(127 )10 ；（3）(0.39)10 ;（4）(25.7)10[解]（1）(17)10 =(10001)2 =(11)16 ；（2）(127)10 = (1111111)2 = (7F)16（3）(0.39)10 = (0.0110)2 = (0.6)16；（4）(25.7)10 = (11001.1011)2 = (19.B)16[1.4]写出下列二进制数的原码和补码。

（1）(+1011)2 ；（2）(+00110)2 ；（3）(-1101)2 ；（4）(-00101)2 。

第3章 逻辑代数(习题)

第3章 逻辑代数(习题)
3.7 答案
CD
AB
00 01 11 10
00 1 1
1
01
1
（1） F1 m(0,1,2,4) d(5,6)
BC
11 1
1
10 1 1
1
（2） F2 m(3,5,6,7,10) d(0,1,2,4,8)
CD
AB
00 01 11 10
00 x x 1 x
(a)
BC
A
00 01 11 10
0 11
表 T3.4（3表）T3.4（3） A B CA FB C F 0 0 00 0 0 0 0 0 10 10 1 1 0 1 00 01 0 0 0 1 10 1 1 1 1 0 01 0 0 0 1 0 11 0 1 0 1 1 01 1 0 1 1 1 11 1 1 1
（3）
A
表 T3.4（1）
ABCD ABCD ABCD ABC D ABCD ABCD
3.2 答案
（1） 左边 AB B AB AB B A B 右边 （2） 左边 A B CCD (B C)(ABD BC)
（A B C） CD ABCD BC
A B C C D ABCD BC A B 1 D ABCD BC 1 右边
0 0 0X 0Y 1Z 1F
O 000 0
B
0 0 1 0 10 01 01
O
010 1
C
011 0
0 1 0 1 10 00 10
O
101 1
F 0 1 0 1 11 00 00
O
111 1
表 T3.4（2）
1 1A B C F t 000 0
1 10 0 1 1
0 1 0t 1

《数字逻辑》第3章习题答案

《数字逻辑》第3章习题答案
习
题
【3-1】填空： (1) 逻辑代数中有三种最基本运算： 与 、 或 和 非 ，在此基础上又派生出五种基本运算， 分别为 与非 、 或非 、 异或 、 同或 、和 与或非 。 (2) 与运算的法则可概述为：有 0 出 0 ，全 1 出 1 ；类似地，或运算的法则为 有”1”出”1”， 全”0”出”0” 。 (3) 摩根定理表示为： A B = A B ； A B = A B 。 (4) 函数表达式 Y= AB C D ，则其对偶式为 Y ' = ( A B)C D 。 积的形式结果应为 M ( 0,1,2,4,5,8,9,10)。 (5) 函数式 F=AB+BC+CD 写成最小项之和的形式结果应为 m ((3,6,7,11,12,13,14,15))， 写成最大项之
0 0 1 1 1 1
1 1 0 0 1 1
0 1 0 1 0 1
1 1 0 0 1 0
【3-8】写出下列函数的反函数 F ，并将其化成最简与或式。 (1) F1 ( A D )( B C D)( AB C ) (2) F2 ( A B )( BCD E )( B C E )(C A) (3) F3 A B C A D (4) F4 ( A B)C ( B C ) D 解： (1) F1 AD C (2) F2 AB A C E (3) F3 AB AC A D (4) F4 BC C D ABD A B C 【3-9】用对偶规则，写出下列函数的对偶式 F ，再将 F 化为最简与或式。 (1) F1 AB B C A C (2) F2 A B C D (3) F3 ( A C )( B C D)( A B D) ABC (4) F4 ( A B )( A C )( B C )(C D) (5) F5 AB C CD BD C 解：题中各函数对偶函数的最简与或式如下： (1) F1 A BC AB C (2) F2 A B D A C D (3) F3 AC A BD (4) F4 A BC B C CD (5) F5 ABC D (6) F6 AB C D 【3-10】已知逻辑函数 F A B C , G=A⊙B⊙C，试用代数法证明： F G 。 解：

数电 逻辑代数基础练习题

数电 逻辑代数基础练习题
第 20 页
数字电子技术
第 1 章 逻辑代数基础
单项选择题
20、当变量 A、B、C 取值为101 时，下列三变量函数最小项中等于
1 的是
( )。
A m1
×
B m3
×
C m5
√
D m7
×
分析提示
将 ABC = 101 代入各最小项： m 1AB C1010 m3ABC 1010 m5ABC1011 m 7AB 1C 010
第 30 页
数字电子技术
第 1 章 逻辑代数基础
单项选择题
30、函数 Y = ABC + ABC + ABC + ABC 的最简化简结果为 ( ) 。
须先变换成同一进制，再比较大小、相等关系。
如统一表示成十进制数：
( 101111 ) 2 = ( 47 ) 10 ( 3A ) 16= ( 58 ) 10
( 55 ) 8= ( 45 ) 10 ( 01010110 ) 8421BCD= ( 56 ) 10
第2页
数字电子技术
第 1 章 逻辑代数基础
8
6
9
3
3
3
5
3
6
第4页
数字电子技术
第 1 章 逻辑代数基础
单项选择题
7、常用的BCD码有8421码、2421码、余3码等，其中既是有权码
又是自补码的是
( )。
A 8421码 C 余3码
×
B 2421码
√
×
D 余3循环码
×
分析提示
2421码代码中从左至右每一位的权分别为 2、4、2、1，为有 权码； 2421码代码中 0和9、 1和8、 2和7、 3和6、 4和5 互 补， 为自补码。

第3章 逻辑代数基础-习题答案

第3章 逻辑代数基础-习题答案
Aห้องสมุดไป่ตู้ B BC BCD ABCD ABCD A BCD BCD B BC BCD A BD B A B D
（3） ( A + B)(B + D)(C + D)( A + C + D)(B + C + D) 解：原式取对偶
F AB BD C D AC D BCD AB BD C D BCD AD AB BD C D BC AD AB BD C BD AD AB BD C AD 冗余定理 =BD C AD
2
(
)
解： F = ABC + ABC + BCD + BCD
F = ( A + B + C)( A + B + C)(B + C + D)(B + C + D)
（5） F = ( A + B)(BCD + E)(C + A) 解： F AB ( B C D) E AC （6） F = ( A + D)(B + C + D)( AB + C) 解： F = AD + BCD + ( A + B)C （7） F = BC + AB + ABC 解： F = ( B + C)( A + B)( A + B + C) （8） F = A + B + D + C 解： F = AB DC 3.6 将下列函数写成与非-与非式。 （1） XY X Z Y Z 解： XY X Z Y Z XY X Z Y Z XY X Z Y Z （2） XYZ X Y Z 解： XYZ X Y Z XYZ X Y Z XYZ X Y Z （3） A + C + D + ABCD + ABC D 解：

第3章 逻辑代数基础答案.docx

第3章 逻辑代数基础答案.docx

第3章逻辑代数习题33. 1求下列函数的反函数(1) F = AB + C(A + D)(2)y = A(万+ C万+ CD)解：(1)F = AB + C(A + D)=AB*C(A + D)= (A + B)*(C + AD)=AC + BC + ABD(2)F = AB + C(A + D)=AB*C(A + D)= (A + B)*(C + AD)=AC + BC + ABD3. 2求下列函数的对偶式(1)Y = AB* CD* DAB(2)Y = A + C + B + C + A + B + B + C解：(1)Y = AB* CD* DABY'=A + B + C + D + D + A + B(2)Y = A + C + B + C + A + B + B + CY'=ACB^CABB^C3. 3用基本定理和公式证明下列等式(1)ABC + ABC + ABC = AB + AC(2)AB+ AC+ BC AB + C(3)A万+ BD + AD + DC^A万+ Z)(4)BC + D +万(万 + C)(DA + B) = B + D(5)AB + AB + AB + AB = 1(6)(A + B)(A + B)(A + B)(A + B) = 0(7) AB + BC + CA = AB + BC + CA(8)(A + B + C) • AB + BC + CA + ABC = (A + 万 +。

・(AB + BC + CA) + 云万©(9)A©B©C=A0BOC(10)A®B = AQB证明：(1)ABC + ABC + ABC = AB + AC左式=ABC + ABC + ABC=(ABC + ABC) + (ABC + ABC)-AB(C + C) + AC(B + B)=AB + AC =右式(2)AB+ AC+ BC AB + C左式= AB + AC + BC=AB + AC(B + B) + BC=AB + ABC + ABC + BC= B(A + AC) + B(AC + C)=AB + BC + BC=AB + C =右式(3)A万+ BD + AD + DC^AB + D左式=A万+ 切+ l£)+ OC=AB + BD + A(B + B)D + DC=B(A + AZ)) + BD + ABD + DC=AB + BD + BD + ABD + DC=AB+D+ABD+DC=AB + D =右式(4)BC + D +万(万 + C)(DA + B) = B + D左式= BC + D + D(B + C)(DA + B)=BC + D + BD(B+ C}=BC+D+BCD=BC+D+BC=B + D =右式(5)AB + AB + AB + AB = 1&^ = AB + AB + AB + AB=A(B + B) + A(B + B)= A + A=]=右式(6)(A + B)(A + 万)Q + B)Q + 万)=0左式=(A + fi)(A + B)(A + B)(A + 万)=(A + B)(A + B)(A + B)(A + B)=(A + B) + (A + B) + (A + B) + (A + B)=AB + AB + AB + AB=1 = 0 =右式(7)AB + BC + CA = AB + BC + CA根据代入规则，令A=B，，B=C，，C=A，左式= AB + BC + CA= B'C'+C'A'+ A'B'再次利用代入规则可得左式= B'C'+C'A' + A'B'= XB + §C + C如右式(8)(A + 5 + C) • AB + BC + CA + ABC = (M + 万 + C)・(AB + BC + CA) + ~ABC左式=(A + B + C) • AB + BC + CA + ABC=(A + B + C) • AB + BC + CA + ABC= (A + B + C)*(AB + BC + CA) + ABC=右式(9)A©B©C=AOB©C左式=A㊉3㊉C= A©BC + (A ㊉B R= (AOB)C+(A©5)C=A©BOC=右式(10)万= AOB左式=A®B= AB + AB-AB+AB=A0B(11)若A®B = C则= A®C = B由A©5 = A5 + A5 = CnJMB(AB + AB) = BC B* AB + AB = 5C艮"万=BC AB = BC将以上两式相加得配+ BC = A(B + B)即B©C=A同理可MA © C = B3.4 设Y ,= Z…, (0, 4,8, 12), %=£,“(1,4, 7,9, 10),试求下列逻辑函数：(1) A =匕+匕(2)L2 =匕•匕(3)L} =Y X・K解：(1)Lj = Kj + Y2A=匕+匕= £〃?(0,4,8,12) + £〃?(l,4,7,9,10)= £〃?(0,l,4,7,8,9,10,12)(2)L2 =Y t»Y2右=约•匕= £m(0,4,8,12)・£m(l,4,7,9,10)= £m(4)(3)L} =Y X・KA=K况=£m(0,4,8,12)・却1,4,7,9,10)= £〃?(0,8,12)3.5已知Y,=riM (0,2, 4, 6), 丫亓日心(1, 3, 5, 7),试求下列逻辑函数:(1) A =匕+七(2)L2 =匕・*(3)£3 =工•匕(4)L4=1T«K解:匕=f[M(0,2,4,6)= £m(0,2,4,6)K = f[M(l,3,5,7)= £〃?(1,3,5,7)(1)Lj = Kj + Y2A=匕+匕=E=0(2)L2 =匕•匕= X+Y；= £m(0,2,4,6) + £m(l,3,5,7)=0(3)L3=K•匕♦ X •七=K・M= £〃？(0,2,4,6)・£〃？(l,3,5,7)= £m(0,2,4,6)(4)L4=Y[»Y^乙4="= £m(0,2,4,6)・£m(l,3,5,7)3.6试写出图P3. 6所示电路的逻辑函数表达式。

第三章 逻辑代数基础 作业题(参考答案)

第三章 逻辑代数基础 作业题(参考答案)

第三章逻辑代数基础(Basis of Logic Algebra)1.知识要点逻辑代数(Logic Algebra)得公理、定理及其在逻辑代数化简时得作用;逻辑函数得表达形式及相互转换;最小项(Minterm)与最大项(Maxterm)得基本概念与性质;利用卡诺图(Karnaugh Maps)化简逻辑函数得方法。

重点:1.逻辑代数得公理(Axioms)、定理(Theorems),正负逻辑(Positive Logic, Negative Logic)得概念与对偶关系(Duality Theorems)、反演关系(plement Theorems)、香农展开定理,及其在逻辑代数化简时得作用;2.逻辑函数得表达形式:积之与与与之积标准型、真值表(Truth Table)、卡诺图(Karnaugh Maps)、最小逻辑表达式之间得关系及相互转换;3.最小项(Minterm)与最大项(Maxterm)得基本概念与性质;4.利用卡诺图化简逻辑函数得方法。

难点:利用卡诺图对逻辑函数进行化简与运算得方法(1)正逻辑(Positive Logic)、负逻辑(Negative Logic)得概念以及两者之间得关系。

数字电路中用电压得高低表示逻辑值1与0,将代数中低电压(一般为参考地0V)附近得信号称为低电平,将代数中高电压(一般为电源电压)附近得信号称为高电平。

以高电平表示1,低电平表示0,实现得逻辑关系称为正逻辑(Positive Logic),相反,以高电平表示0,低电平表示1,实现得逻辑关系称为负逻辑(Negative Logic),两者之间得逻辑关系为对偶关系。

(2)逻辑函数得标准表达式积之与标准形式(又称为标准与、最小项与式):每个与项都就是最小项得与或表达式。

与之积标准形式(又称为标准积、最大项积式):每个或项都就是最大项得或与表达式。

逻辑函数得表达形式具有多样性,但标准形式就是唯一得,它们与真值表之间有严格得对应关系。

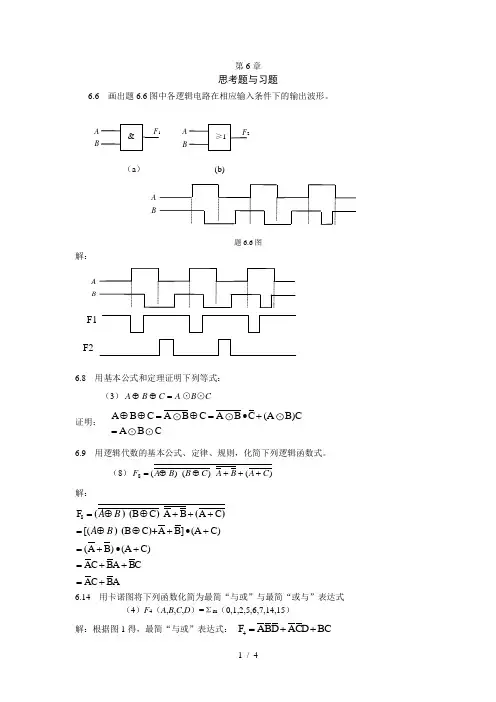
逻辑代数基础课后习题答案

逻辑代数基础课后习题答案

第6章思考题与习题6.6 画出题6.6图中各逻辑电路在相应输入条件下的输出波形。

（a ） (b)题6.6图解：A BF1F26.8 用基本公式和定理证明下列等式： （3）A C B A =⊕⊕⊙B ⊙C 证明：A B C A B C A B C (A B)CABC⊕⊕=⊕=•+=6.9 用逻辑代数的基本公式、定律、规则，化简下列逻辑函数式。

（8）)()()(8C A B A C B B A F +++⊕⊕= 解：8F B C A B A C [(B C A B](A C)(A B)(A C)AC BA BC AC BA()()())()+A B A B =⊕⊕+++=⊕⊕+•+=+•+=++=+6.14 用卡诺图将下列函数化简为最简“与或”与最简“或与”表达式（4）F 4（A ,B ,C ,D ）=Σm （0,1,2,5,6,7,14,15）解：根据图1得，最简“与或”表达式： 4F ABD ACD BC =++F 1 。

F 2。

A B根据图2得，最简“或与”表达式：4F BCD AC AB BCD (B C D)(A C)(A B)(B C D)=+++=++++++6.16 用卡诺图将下列函数化简为最简“与或”式（2）F 2（A ,B ,C ,D ）=Σm （1,3,4,9,11,12,14,15）+Σd （5,6,7,13）（3）D C B A ABC C B A F ++=3，约束条件0=⊕B A 解：（2）根据图1：F 2=B+D约束条件：A C A A C B D BCD BCD AB D=0+++（3）根据图2：3F AC BC CD =++，约束条件0=⊕B A6.21 写出题6.21图所示各电路的逻辑表达式，化成最简“与或”式，并用“与非”门重新实现。

6.21图图1图2F 1。

F 2（a ）（b ）解：1F A B BC A B)BC=ABC BC=BC (=++=++)()C 2F A B+B+C A B B+C AB AB B C AB AB =⊕=⊕•=++=+（）（用“与非”门实现：6.28 已知逻辑函真值表如图表题6.28所示，写出逻辑函数式，化简并用“与非”门实现。

逻辑代数基础试题及答案

逻辑代数基础试题及答案

逻辑代数基础试题及答案1. 逻辑代数中，与运算的符号是什么？答案：与运算的符号是“∧”。

2. 逻辑代数中，或运算的符号是什么？答案：或运算的符号是“∨”。

3. 逻辑代数中，非运算的符号是什么？答案：非运算的符号是“¬”。

4. 逻辑代数中，异或运算的符号是什么？答案：异或运算的符号是“⊕”。

5. 逻辑代数中，同或运算的符号是什么？答案：同或运算的符号是“≡”。

6. 逻辑代数中，如何表示变量A和变量B的与运算？答案：变量A和变量B的与运算表示为“A∧B”。

7. 逻辑代数中，如何表示变量A和变量B的或运算？答案：变量A和变量B的或运算表示为“A∨B”。

8. 逻辑代数中，如何表示变量A的非运算？答案：变量A的非运算表示为“¬A”。

9. 逻辑代数中，如何表示变量A和变量B的异或运算？答案：变量A和变量B的异或运算表示为“A⊕B”。

10. 逻辑代数中，如何表示变量A和变量B的同或运算？答案：变量A和变量B的同或运算表示为“A≡B”。

11. 在逻辑代数中，德摩根定律是什么？答案：德摩根定律包括两个部分，即(¬A)∨(¬B) = ¬(A∧B)和 (¬A)∧(¬B) = ¬(A∨B)。

12. 逻辑代数中，如何证明A∧(A∨B) = A？答案：根据分配律，A∧(A∨B) = (A∧A)∨(A∧B)。

由于A∧A = A，所以表达式简化为A∨(A∧B)。

由于A∨A = A，最终表达式简化为A。

13. 逻辑代数中，如何证明A∨(¬A∧B) = A∨B？答案：根据分配律，A∨(¬A∧B) = (A∨¬A)∧(A∨B)。

由于A∨¬ A = 1（真），表达式简化为1∧(A∨B)。

由于任何变量与1的与运算结果都是该变量本身，最终表达式简化为A∨B。

14. 逻辑代数中，如何证明A∧(¬A∨B) = ¬A∨B？答案：根据分配律，A∧(¬A∨B) = (A∧¬A)∨(A∧B)。

人邮社数字电路逻辑设计习题答案

人邮社数字电路逻辑设计习题答案
9．将下列十进制数转换成二进制数、八进制数和十六进制数（精确
到二进制小数点后4位）。 答案：（1）（1000001）2
（2）（0.0100）2，
（3）（100001.0101）2 10．写出下列各数的原码、 答案：（1）原码=反码=补码=0.1011
（2）原码=1.1100， 反码=1.0011，补码=1.0100（3）原码=110110，反码=101001，补码=101010
7．按二进制运算法则计算下列各式。
答案：（1）110001（2）110.11（3）10000111（4）101 8．将下列二进制数转换成十进制数、八进制（2）（0.8281）10， （0.65）8，
（3）（23.25）10， （27.2）8，
5．采用余3码进行加法运算时，应如何对运算结果进行修正？为什
么？
答案：两个余3码表示的十进制数相加时，对运算结果修正的方 法是：如果有进位，则结果加3；如果无进位，则结果减3。为了解 决四位二进制运算高位产生的进位与一位十进制运算产生的进位之 间的差值。
6．奇偶检验码有哪些优点和不足？ 答案：奇偶检验码的优点是编码简单，相应的编码电路和检测电 路也简单。缺点是只有检错能力，没有纠错能力，其次只能发现单错， 不能发现双错。
理和规则十分熟练时化简比较方便；缺点是没有固定的规律和步骤， 技巧性强，且通常难以判断化简结果是否达到了最简单。9．用卡诺图化简逻辑函数时，应如何画卡诺圈才能求得一个函数的 最简与—或表达式？
答案：注意两点： 第一，在覆盖所有1方格的前提下，卡诺圈的 个数应达到最少；第二，在满足合并规律的前提下，每个卡诺圈的大 小应达到最大。
11.已知［N］补=1.0110，求［N］原，［N］反和N。
答案：［N］原码=1.1010,［N］反码=1.0101,N= -0.1010

第三章逻辑代数基础作业题(参考答案)

第三章逻辑代数基础作业题(参考答案)

第三章逻辑代数基础（Basis of Logic Algebra）1．知识要点逻辑代数（Logic Algebra）的公理、定理及其在逻辑代数化简时的作用；逻辑函数的表达形式及相互转换；最小项（Minterm）和最大项（Maxterm）的基本概念和性质；利用卡诺图（Karnaugh Maps）化简逻辑函数的方法。

重点：1．逻辑代数的公理（Axioms）、定理（Theorems），正负逻辑（Positive Logic, Negative Logic）的概念与对偶关系（Duality Theorems）、反演关系（Complement Theorems）、香农展开定理，及其在逻辑代数化简时的作用；2．逻辑函数的表达形式：积之和与和之积标准型、真值表（Truth Table）、卡诺图（Karnaugh Maps）、最小逻辑表达式之间的关系及相互转换；3．最小项（Minterm）和最大项（Maxterm）的基本概念和性质；4．利用卡诺图化简逻辑函数的方法。

难点：利用卡诺图对逻辑函数进行化简与运算的方法（1）正逻辑（Positive Logic）、负逻辑（Negative Logic）的概念以及两者之间的关系。

数字电路中用电压的高低表示逻辑值1和0，将代数中低电压（一般为参考地0V）附近的信号称为低电平，将代数中高电压（一般为电源电压）附近的信号称为高电平。

以高电平表示1，低电平表示0，实现的逻辑关系称为正逻辑（Positive Logic），相反，以高电平表示0，低电平表示1，实现的逻辑关系称为负逻辑（Negative Logic），两者之间的逻辑关系为对偶关系。

（2）逻辑函数的标准表达式积之和标准形式（又称为标准和、最小项和式）：每个与项都是最小项的与或表达式。

和之积标准形式（又称为标准积、最大项积式）：每个或项都是最大项的或与表达式。

逻辑函数的表达形式具有多样性，但标准形式是唯一的，它们和真值表之间有严格的对应关系。

逻辑代数基础习题解答

逻辑代数基础习题解答
组合逻辑电路中的竞争与冒险
分析电路中可能出现的竞争与冒险现象，采取相应措施进行消除或 抑制。
时序逻辑电路分析与设计
分析时序逻辑电路
了解时序逻辑电路的基本概念和组成，包括触发器、寄存器、计数器等。根据给定的电路图，分 析电路的工作原理和功能。
设计时序逻辑电路
根据实际需求，确定输入与输出之间的逻辑关系以及电路的状态转换关系。选择合适的触发器类 型，设计状态转换表和状态转换图，并进行电路连接。
备考策略指导
明确考试要求
了解考试形式和评分标准，明确备考方向和重 点。
制定复习计划
根据考试要求和自身情况，制定合理的复习计 划，并按照计划有序进行复习。
多做模拟试题
通过做模拟试题来检验自己的学习成果，找出自己的不足之处，有针对性地进 行弥补。
考试技巧点拨
仔细审题
在考试时，认真阅读题目，理解题意和要求 ，避免因为误解题意而导致失分。
题目1：逻辑代数中，基本的逻辑运算包括哪些？
02
A. 与、或、非
03
B. 与、或、异或
选择题解析
C. 与、非、同或 D. 或、非、异或 答案：A. 与、或、非
选择题解析
• 题目2：在逻辑代数中，下列哪个公式是正 确的？
选择题解析
C. A + A'B = A + B
B. A(A + B) = AB
表示方法
逻辑函数可以用多种方法表示，如真值表、逻辑表达式、卡诺图等。其中，真值表是列出所有输入组合及对应输 出的表格；逻辑表达式是用逻辑运算符和逻辑变量表示的式子；卡诺图是一种图形化表示方法，用于简化逻辑函 数。
02 逻辑代数化简方法
公式化简法
利用基本公式进行化简

数电各章复习题及答案.

数电各章复习题及答案.

第1章逻辑代数基础一、选择题（多选题）1．以下代码中为无权码的为。

A. 8421BCD码B. 5421BCD码C. 余三码D. 格雷码2．一位十六进制数可以用位二进制数来表示。

A. １B. ２C. ４D. 163．十进制数25用8421BCD码表示为。

A.10 101B.0010 0101C.100101D.101014．与十进制数（53.5）10等值的数或代码为。

A.(0101 0011.0101)8421BCDB.(35.8)16C.(110101.1)2D.(65.4)85.与八进制数(47.3)8等值的数为：A. (100111.011)2B.(27.6)16C.(27.3 )16D. (100111.11)26.常用的B C D码有。

A.奇偶校验码B.格雷码C.8421码D.余三码7.与模拟电路相比，数字电路主要的优点有。

A.容易设计B.通用性强C.保密性好D.抗干扰能力强8. 逻辑变量的取值１和０可以表示：。

A.开关的闭合、断开B.电位的高、低C.真与假D.电流的有、无9．求一个逻辑函数F的对偶式，可将F中的。

A .“·”换成“+”，“+”换成“·”B.原变量换成反变量，反变量换成原变量C.变量不变D.常数中“0”换成“1”，“1”换成“0”E.常数不变10. A+BC= 。

A .A+B B.A+C C.（A+B）（A+C） D.B+C11.在何种输入情况下，“与非”运算的结果是逻辑0。

A．全部输入是0 B.任一输入是0 C.仅一输入是0 D.全部输入是112.在何种输入情况下，“或非”运算的结果是逻辑0。

A．全部输入是0 B.全部输入是1 C.任一输入为0，其他输入为1 D.任一输入为113.以下表达式中符合逻辑运算法则的是。

A.C·C=C2B.1+1=10C.0<1D.A+1=114. 当逻辑函数有n个变量时，共有个变量取值组合？A. nB. 2nC. n2D. 2n15. 逻辑函数的表示方法中具有唯一性的是。

西工大逻辑代数基础作业答案

西工大逻辑代数基础作业答案

西工大逻辑代数基础作业答案
1．在式子n-3、a2b、m+s≤2、x、﹣ah、s＝ab中代数式的个数有() [单选题] * A．6个
B．5个
C．4个(正确答案)
D．3个
2．下列代数式书写正确的是() [单选题] *
A．a4
B．m÷n
C．x(b+c)(正确答案)
3．代数式的意义是() [单选题] *
A．x除以y加3
B．y加3除x
C．y与3的和除以x
D．x除以y与3的和所得的商(正确答案)
4．若x表示某件物品的原价，则代数式(1+10%)x表示的意义是() [单选题] * A．该物品打九折后的价格
B．该物品价格上涨10%后的售价(正确答案)
C．该物品价格下降10%后的售价
D．该物品价格上涨10%时上涨的价格
5. 购买2个单价为a元的面包和5瓶单价为b元的饮料，所需钱数为() [单选题] *
A．(2a+b)元
B．3(a+b)元
C．(5a+2b)元
D．(2a+5b)元(正确答案)。

数字电子技术基础课后答案全解

数字电子技术基础课后答案全解

【 3-5】用卡诺图化简下列带有约束条件的逻辑函数
（1） P1 A, B, C, D
m(3,6,8,9,11,12)
(0,1,2,13,14,15) AC BD BCD (或ACD)
d
(2) P2(A,B,C,D)= m(0,2,3,4,5,6,11,12)
(8,9,10,13,14,15) BC BC D
有” 1”
4、摩根定理表示为： A B = A B ； A B = A B 。
5、函数表达式 Y= AB C D ，则其对偶式为 Y = ( A B)C D 。
6、根据反演规则，若 Y= AB C D C ，则 Y ( AB C D) C 。
7、指出下列各式中哪些是四变量 A B C D 的最小项和最大项。在最小项后的（
(1) F1 = ABC AB 1
(2) F2 = ABCD ABD ACD AD
(3) F3 AC ABC ACD CD A CD
(4) F4 A B C ( A B C ) ( A B C ) A BC
【 3-3】 用卡诺图化简下列各式
(1) F1 BC AB ABC AB C
(3) F3 AC AC BC BC AB AC BC
第 3 页 /共 46 页
CMOS
A F1
10k
(a)
TTL
A
B
F2
100
(b)
CMOS
A
B
F3
51
(c)
TTL
A
B
F4
100k
CMOS
A
B
F5
10k
(d)
解： (a) F1 A (b)
(e) 图 4.4

数字逻辑第三章习题答案

数字逻辑第三章习题答案
Leabharlann &E D C
A B C
Y0 Y1 Y2 Y3 Y4 Y5 Y6 Y7
&
G
3.21 F = X⊕Y⊕Z X 0 0 1 1 3.22 ⑴
74138 Y0 Y1 Y2 Y3 Y4 Y5 Y6 Y7 Y X & F Z Z A B Y C0 C1 C2 C3 74153 F
74153
Y 0 1 0 1
F Z Z Z Z
74LS283
S3 S2 S1 S0
Y2Y4Y2Y1
3.29 ⑴ 当B=1时 F = C+C 静态 险象 静态1险象 时 静态1险象 当A=1,C=0 时 F = B+B 静态 险象 化简F 可消除险象。 化简 = B + AC 可消除险象。 静态1险象 ⑵ 当 B=C=D=1时 F = A+A 静态 险象 时 静态1险象 当 A=C=0 时 F = B+B 静态 险象 静态1险象 当 A=D=1,B=0 时 F = C+C 静态 险象 F = AB + BC + ACD + AC + BCD + ABD 可消除险象。 可消除险象。 3.30 ⑴ F=AB+CD+BCD+ACD ⑶ F=BD+BD+ABC+ACD
+5V
AGTB AGTB AEQB AEQB ALTB ALTB A0 B0 74LS85 A1 B1 A2 B2 A3 B3
X>Y X=Y X<Y
••• •••
••• •••
+5V
X12 Y12 X13 Y13 X14 Y14 X15 Y15
3.26 ⑸ 2421码→8421码 码 码 A = 0：+ 0000 A = 1：－ 0110（+ 1010） A B C D

数字电子电路与逻辑 刘可文主编 第三章 逻辑代数基础 答案

数字电子电路与逻辑 刘可文主编 第三章 逻辑代数基础 答案

习 题3题3.1写出下述逻辑表达的真值表。

（1）L=C B D B C A ++⋅， （2）L=B C D A C B ++， （3）L= B A C B C A ++⋅， （4）L=C B A C B A C B A ++， （5）L= B A +， （6）L=D B C B A CD B ++ （7）L= BC A C AB C AB ++， （8）L= C A C A +， （9）L= BC A C AB C AB ++， （10）L= B A C B C A ++。

解：各个小题所对应的逻辑表达式的真值表如表3.1（1）、（2）、（3）、（4）、（5）、（6）、（7）、（8）、（9）、（10）所示。

D B A C B A CD B 表3.1 (7)L=表3.1 (2) L=B C D A C B ++的真值表（1）A ⊙0=A ， （2）0A ⊕=A ， （3）A ⊙1=A ， （4），A 1A =⊕ （5）0A A =⊕，（6）1A A =⊕， （7）A ⊙A=1， （8）A ⊙A =0，（9）)A B (C )C A (B C )B A (⊕⊕=⊕⊕=⊕⊕， （10）)B C ()AC (C )B A (⊕=⊕，（11）A ⊙(B ⊙C)= B ⊙(A ⊙C)， （12）A +(B ⊙C)＝(AB ⊙AC)。

解：题3.2（1～12）的各个等式的真值表如表3.2（1）、（2）、（3）、（4）、（5）、（6）、（7）、（8）、（9）、（10）、（11）、（12）所示。

从表3.2（1）、（2）、（3）、（4）、（5）、（6）、（7）、（8）、（9）、（10）、（11）、（12）所示真值表的对应关系，可以证明命题各式成立。

表3.1 (8)L= C B A C B A +的真值表表3.1 (9) L=BC A C AB C AB ++的真值表表3.1 (10) L=B AC B C A ++的真值表表3.2 （1）真值表表3.2 （2）真值表 表3.2 （3）真值表 表3.2 （5）真值表 表3.2 （6）真值表表3.2 （4）真值表表3.2 (9) L=的真值表题3.3逻辑式A ⊕B ⊕C 的对偶式是。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第3章 逻辑代数基础3.1 已知逻辑函数真值表如题表3.1所示，写出函数对应的标准与或表达式和标准或与表达式。

解： (0,1,4,5)()()()()(2,3,6,7)F A B C A B C A B C A B C A B C A B C A B C A B C =+++==++++++++=∑∏3.2 写出下列函数的标准与或式和标准或与式。

（1）()()()X A B D A C D B C D =++++++ 解：（先求标准或与式，得最大项；最大项中没有的编号构成最小项，组成标准与或式）()()()()()()()()(0,1,2,6,14)(3,4,5,7,8,9,10,11,12,13,15)X A B D A C D B C D A B C D A B C D A B C D A B C D A B C D =++++++=+++++++++++++++==∑∏ （2） X BCD AC D A C D A B D =+++ 解：（先求标准与或式，得最小项；最小项中没有的编号构成最大项，组成标准或与式）(0,2,4,7,8,12,15)(1,3,5,6,9,10,11,13,14)X BCD AC D A C D A B DABCD ABCD ABC D AB C D ABC D A B C D A BC D =+++=++++++==∑∏3.3 使逻辑函数()()()()()X A B B C A C A C B C =+++++为0的逻辑变量组合有哪些？使之为1的逻辑变量组合有哪些？ 解：()()()()()()()()()()()(1,2,3,4,5,6)(0,7)X A B B C A C A C B C A B C A B C A B C A B C A B C A B C =+++++=++++++++++++==∑∏ 使函数为0的组合即最大项，有ABC =“110”，“101”，“100”，“011”，“010”，“001”；使之为1的逻辑变量组合有ABC =“000”，“111”。

3.4 写出下列函数的对偶式。

（1）()()()()F A B A B B C A C =++++ 解：'F AB AB BC AC =+++（2）F A B C =++ 解：'F A BC =⋅（3）C B A F +⋅= 解：'F A BC =+题表3.1A B C F 0 0 0 1 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 1 1 0 1 1 1 1 0 0 1 1 13.5 写出下列函数的反函数。

（1）E D C B A F ++++= 解：F A BC DE =⋅⋅（2）])[(E A D C B F ++= 解：()F B C D AE =++ （3）D C B A F += 解：()()F A B C D =++3.6 将下列函数写成与非-与非式。

（1）Z Y Z X XY ++解： XY XZ Y Z XY XZ Y Z XY XZ Y Z ++=++=⋅⋅（2）Z Y X XYZ +解： XYZ X Y Z XYZ X Y Z XYZ X Y Z +=+=⋅3.7 将下列函数写成或非-或非式。

（1）))((C B B A ++解：()()()()A B B C A B B C A B B C ++=++=+++（2）))()((D C B D C A C B A ++++++解：()()()A B C A C D B C D A B C A C D B C D ++++++=++++++++3.8 用公式法化简下列逻辑函数。

（1）Z XY Y X XYZ ++ 解：1F XY XY Y =+= （2）Y X Y X +⋅+ 解：20F X Y XY =⋅=（3）C B A C AB BC A C B A ABC ++++ 解：3 ()F AB AC A B BC A B AB =++=++或 （4）AB CD A A D C ++++解：4()F C D A A CD C D A CD A C D =+++=+++=++（5）))()()((B A D C A D C A D C A +++++++ 解：5()()()F A C A D A B A BCD =+++=+ （6）C AB C B BC A AC +++解：6F AC BC BC ABC C ABC C =+++=+= （7）1ABC BD A D +++ 解：71F =（8）) (CD B A B A B A AB +⋅++解：8()()F A B A B CD A B A B CD A B =+⋅+=⋅+=（9）D C B A CD B A D C B C B B A +解：9F A B BC BCD A BCD A B CD A B A BD A B D =+++++=++=++（10）D C D B C A ABC )( ++解：10F ABC A C BD C D A B C D =+++++=+++3.9 证明下列异或运算公式。

（1）A A =⊕0证明：0000A A A A A ⊕=⋅+⋅=+= （2）A A =⊕1证明：1110A A A A A ⊕=⋅+⋅=+=（3）0=⊕A A证明：0A A A A A A ⊕=⋅+⋅=（4）1=⊕A A证明：1A A A A A A A A ⊕=⋅+⋅=+=（5）A B A AB =⊕证明：()()AB AB AB AB AB AB A B AB AB A B AB AB A ⊕=⋅+⋅=+⋅+⋅+=+=3.10 证明下列等式成立。

（1）A ⊙B A B ⊕=证明：A B A B A B A B A B A B ⊕=⋅+⋅=⋅+⋅=:（2）B A B A ⊕=⊕证明：A B A B A B A B A B A B A B A B ⊕=⋅+⋅=⋅+⋅=⋅+⋅=⊕（3）=⊕⊕C B A A⊙B⊙C证明：()()()()A B C AB AB C AB AB CA B A B C ABC AB C ABC ⊕⊕=+⋅++⋅=++++=+++ A⊙B⊙C=C B A AB C B A AB ⋅++⋅+)()( =C B A ABC C B A B A ++++))(( =C B A ABC C B A C B A +++ 3.11 化简下列各式为最简或与式。

（1）))()()()((C B C A C A C B B A X +++++= 解：)X AB BC AC AC BC AB AC BC′=++++=++()()()()()()X A B A C B C or A B A C B C =+++=+++（2）))()()()((D C B D C A D C D B B A X +++++++= 解：()()X AB BD CD ACD B CDAB B B C D C AC DAB BD C AD BD C AD′=++++=++++=+++=++ ()()X B D A D C =++（3）))()()((D B A D C A D C A D C B X ++++++++=X3.11 (1)解：()()X B C D =+++++3.12 化简下列各式。

（1）AC C B AB G ++=解：()()G AB BC A B B C AB A C B C AB B C =⋅=++=++=+ （2）))()()((D C A D C A D C B D C A G ++++++++=解：G ACD BC D ACD ACD CD BC D ACD CD BD ACD =+++=++=++ （3）D C B C B A G )()(⊕+⊕=解：()()()()G A B C B C D AB A B C BC BC D ABC ABD A BC A B D BC C D A BC ABD A B D BC C D A BC ABD BC C D=++=++++=+++++=++++=+++::3.13 逻辑函数项W XYZ 的相邻项有哪些？ 解：,,,.W XYZ WXYZ W X YZ W XY Z3.14 画出下列函数的卡诺图，分析每组函数间的关系。

（1）Z X Y X F +=1))((2Y X Z X F ++=解：12F F ∴=。

（2）C B A ABD C B A D B A G +++= 1))()()((2D C B D C A D C B D C A G ++++++++= 解：12G G ∴=3.15 用卡诺图化简下列函数，并求出最简与或表达式。

（1）1(,,)(2, 3, 6,7)F X Y Z =∑ 解：1F Y =（2）2(,,,)(7, 13, 14, 15)F A B C D =∑ 解：2F ABC BCD ABD =++（3）3(,,,)(1, 3, 4, 6, 7, 9, 11, 12, 14, 15)F A B C D =∑F 1F 2G 1 G 2解：3F BD BD BC =++ 或 3F BD BD CD =++3.16 用卡诺图化简下列函数，并求出最简与或式。

（1）D B A CD A B A D C A ABD F 1++++= 解：1F A C D AB D ACD AB BD =++++或 1F B C D AB D ACD AB BD =++++ （2）)(2Y X Y X W Y X W Z X F +++= 解：2F XY XZ W XY =++（3）E D C B C B A CE B A CDE D C B BDE F 3+++++= 解：3F B CE B CD A BC DE =+++3.17 用卡诺图化简下列函数，并求出最简或与式。

（1）1(,,)(0, 1, 4,5)F A B C =∏ 解：1F B =（2）2(,,,)(0, 1, 2, 3, 4, 10, 11)F A B C D =∏ 解：2()()()F A B B C A C D =++++（3）3(,,,)(1, 3, 5, 7, 13, 15)F W C Y Z =∏解：3()()F W Z C Z =++3.18 用卡诺图化简下列各式，并求出函数的最简与或式及最简或与式。

（1）XYZ Z Y Z Y Z X F +++= 1 解：1()()F Z XY X Z Y Z =+=++（2）))()()((2D C B D B A D B A D B A F ++++++++=F 1F 2F 3F 1F 2F 3F 1解：2 ()()()F A B D A B C BD AB A B D A CD BD AB B C D A B D A B =++++++=+++++或＝（3）))()()((3D C B A D B A D A D B A F ++++++++= 解：3 ()()()F BD AD A B D ABC BD AD A B D AC D A B D B C D A D =++++++=+++++或3.19 试用最少与非门实现下列逻辑函数。