八年级数学《行知天下》答案
- 格式:pdf
- 大小:7.54 MB
- 文档页数:10

参考答案成长话题交往主题一跳跃的文明交往因子专题一相亲相爱一家人自主感悟“同桌妈妈”感动中国只要能够表达出母爱是世界上最真挚、最无私、最伟大的爱等即可。
孝心无价,感恩永恒只要能够表达出子女应该孝敬父母等即可。
学苑采珠血色母爱〖牛刀小试〗做一做(1)是“家”吸引着在外的游子们。
因为家里有亲人,家中有亲情。
(2)因为①家,是我们每个人最熟悉的地方,在这里有我们亲爱的家人,家人们平等相处,相互关爱;家,是一个充满亲情的地方。
平凡的家庭小事让我们感受着家庭的温暖和幸福;家,是我们温馨的港湾。
②孝敬父母既是道德的要求也是法定的义务,二者是密切联系的。
(3)①漫画反映了社会上有一部分子女,以工作忙等为借口,忽视了孝敬父母,这是违法行为,应当引以为戒。
②帮父母做些力所能及的家务劳动,关心父母的健康,同父母聊聊天等,言之有理即可。
与父母交往的“七招”〖牛刀小试〗试一试:答题方向:言之有理即可,例如:(1)对父母,不隐瞒;说见闻,听意见;(2)对批评,不反感;有则改,无则勉;(3)受表扬,莫骄傲;常思过,胜良药;(4)提要求,莫过高;没满足,不计较。
想一想1.妈妈不尊重小明的兴趣爱好,母子俩缺乏理解和沟通。
小明不能虚心听取父母的批评建议,没有做到换位思考。
2.首先,向妈妈承认自己的错误;其次,向妈妈解释自己考良的原因;再次,向妈妈保证自己上电脑班不会影响自己的学习;最后,要用优异的成绩向妈妈证明自己的决定是正确的。
走进生活调查访谈:略。
建言献策:(1)要尊重父母,热爱父母,回报父母。
(2)要做到日常生活中对父母有礼貌,理解父母的心意,听取父母的教诲,关心父母的健康,体贴父母的辛劳,分担父母的忧愁,不向父母提出过分的要求。
我在行动:计划表项目要具体,切实可行即可。
自我体验:如果我是母亲实地体验:略。
我思我行:略。
美文赏读那个天使叫妈妈母爱是世界上最真挚、最无私的爱,我们做子女的要学会感恩等,言之有女儿的牵挂能够感受到小女孩和爸爸之间深深的爱,言之有理即可。

一、知识宫里任我行。
(20%)1、一亿二千零四万七千零八十写作(),省略万后面的尾数约是()。
2、如果A是B的,A和B的最小公倍数是(),它们的最大分因数是()。
3、4.25小时=()时()分2公顷40平方米=()公顷4、一根木料长1.6米,现在将它锯成同样长的小段,七次锯完,每小段占这根木料的(),每小段长()米。
5、六(1)班第一组同学的体重是45千克、50千克、45千克、51千克、47千克、45千克。
这组数据的众数是(),中位数是()。
6、现有3厘米、4厘米的小棒各一根,请你再选1根长度是整厘米的小棒,围成的三角形的周长最大是()厘米,最小是()厘米。
7、有三把锁和三把钥匙,现在用三把钥匙去打开三把锁,最多要试()次。
8、一个正方体,其中4个面涂红色,一个面涂绿色,一个面涂蓝色,小丁任意抛10次,落下后红色面朝上的可能性是()。
9、一个圆柱体和一个圆锥体等底等高,如果它们的体积相差32立方分米,那么圆锥体的体积为()立方分米。
10、甲数除以乙数的商是1.5,如果甲数增加20,则甲数是乙数的2倍。
原来甲数是()。
11、一个高10厘米的圆柱体,如果把它的高截短3厘米,它的表面积减少94.2平方厘米。
这个圆柱体积是()立方厘米。
12、用火柴棒搭一个三角形,搭1个三角形用3根火柴棒,搭2个三角形用5根火柴棒,搭3个三角形用7根火柴棒,照这样的规律搭50个这样的三角形要()根火柴棒。
二、反复比较,精挑细选。
(将正确答案的序号填在下面的括号里)(10%)1、在自然数中,凡是5的倍数()。
①一定是质数②一定是合数③可能是质数,也可能是合数2、一个圆锥与一个圆柱体的底面周长的比是1:2圆锥的高是圆柱的6倍,圆柱体的体积是圆锥的()。
① 2 倍②③3、甲乙两地实际距离是320千米,在一幅地图上量得的距离是4厘米,这幅地图的比例尺是()①1∶80 ②1∶8000 ③1∶80000004、如果a÷ =b×(a、b都不等于零),那么()。


北京二中教育集团2024—2025学年度第一学期初二数学期中考试试卷考查目标1.知识:人教版八年级上册《三角形》、《全等三角形》、《轴对称》、《整式的乘法与因式分解》的全部内容.2.能力:数学运算能力,逻辑推理能力,阅读理解能力,实际应用能力,数形结合能力,分类讨论能力.考生须知 1.本试卷分为第Ⅰ卷、第Ⅱ卷和答题卡,共16页;其中第Ⅰ卷2页,第Ⅱ卷6页,答题卡7页。
全卷共三大题,28道小题。
2.本试卷满分100分,考试时间120分钟。
3.在第Ⅰ卷、第Ⅱ卷指定位置和答题卡的密封线内准确填写班级、姓名、考号、座位号。
4.考试结束,将答题卡交回。
第Ⅰ卷(选择题共 16分)一、选择题(共16分,每题2分,以下每题只有一个正确的选项)1.中国古典建筑中有着丰富多彩的装饰纹样,以下四个纹样中,不是轴对称图形的是() A.B.C.D.2.下列计算正确的是( )A. B. C. D.3.如图是尺规作图中“画一个角等于已知角”的示意图,该作法运用了“全等三角形的对应角相等”这一性质,那么判定图中两三角形全等的条件是( )A.SSSB.SASC.AASD.ASA 4.如图,在中,边上的高是()32m m m -=326m m m ⋅=624m m m ÷=()239m m =ABC △BCA. B. C. D.5.如图,在中,,于D ,点B 关于直线的对称点是点,若,则的度数为( )A.8°B.10°C.20°D.40°6.已知式子的计算结果中不含x 的一次项,则a 的值为()A. B.3 C.1.5D.07.根据下列已知条件,不能画出唯一的是()A.,, B.,,C.,, D.,,8.如图,和分别是的内角和外角的角平分线,,连接.以下结论:①;②;③;④,其中正确的结论有( )A.1个B.2个C.3个D.4个第Ⅱ卷(非选择题 共84分)二、填空题(共16分,每题2分)9.已知等腰三角形的两条边长分别为2和5,则这个等腰三角形的周长为______.10.若有意义,则x 的取值范围是______.11.如图,摄影师在拍照时为了确保照片的清晰度,往往会放一个三脚架来固定和支撑相机,这里用到的数学道理是______.BD CE BE AFABC △90BAC ∠=︒AD BC ⊥AD B '50B ∠=︒B AC '∠()()23x x a +-3-ABC △10AB =6BC =5CA =10AB =6BC =30A ∠=︒10AB =6BC =60B ∠=︒10AB =6BC =90C ∠=︒BD AD ABC △ABC ∠CAE ∠AD BC P CD AB AC =2BAC BDC ∠=∠4EAC ADB ∠=∠90ADC ABD ∠+∠=︒()021x -12.如图是一个五边形,图形中x 的值为______°.13.如图,在长方形中,,垂足为E ,交于点F ,连接.请写出一对面积相等但不全等的三角形______.14.若,,则______.15.如图,在等腰中,,,,,点C 的坐标是______.16.如图,等边的边长为5,点E 在上,,射线,垂足为点C ,点P 是射线上一动点,点F 是线段上一动点,当的值最小时,的长为______.ABCD AF BD ⊥AF BC DF 3a x =2b x =3a b x +=Rt ABC △90CAB ∠=︒AB AC =2OA =3OB =ABC △BC 2CE =CD BC ⊥CD AB EP FP +BF三、解答题(共68分,其中第17-21,23题每题5分,第22,24,25,26题每题6分,第27-28题每题7分)17.计算:.18.因式分解:.19.因式分解:.20.已知,求代数式的值.21.如图,中,,于点E ,于点D ,与相交于点F .求证:.22.如图,已知.(1)根据要求尺规作图:①作的平分线;②在上取点C ,作边的垂直平分线交于点D ,连接;(要求:保留作图痕迹,不写作法)(2)在(1)所作的图中,求证:.解:平分 垂直平分线段(____________)(填推理依据) (____________)(填推理依据)()2533a a a⋅--2328x y y -()()314x x +-+2410m m --=()()()22311m m m ---+ABC △45ABC ∠=︒BE AC ⊥AD BC ⊥BE AD BF AC =AOB ∠AOB ∠OP OP OC MN OA CD CD OB P OC AOB ∠AOC BOC ∴∠=∠MN OCDO DC ∴=AOC DCO ∴∠=∠BOC DCO ∴∠=∠CD OB∴P23.如图:在平面直角坐标系中,其顶点坐标如下:,,.(1)画出关于x 轴对称的图形.其中A 、B 、C 分别和、、对应;(2)点P 在y 轴上,若为等腰三角形,则满足条件的点P 的个数是______个.24.如图,是等边三角形,于D ,为边中线,,相交于点O ,连接.(1)判断的形状,并说明理由(2)若,求的长.25.如图1有三种纸片,A 种纸片是边长为a 的正方形,B 种纸片是边长为b 的正方形,C 种纸片是长为b ,宽为a 的长方形,老师用A 种纸片一张,B 种纸片一张,C 种纸片两张拼成如图2的大正方形.(1)观察图2的面积关系,写出一个数学公式______;(2)根据数学公式,解决问题:已知,,求的值.26.我们已经学习过多项式除以单项式,多项式除以多项式一般可用竖式计算,例如:计算,可用竖式除法.步骤如下:①把被除式、除式按某个字母降幂排列,并把所缺的项用零补齐;②用被除式的第一项除以除式第一项,得到商式的第一项;③用商式的第一项去乘除式,把积写在被除式下面(同类项对齐),再把两式相减;ABC △xOy ()3,1A -()1,2B --()1,3C ABC △111A B C △1A 1B 1C ACP △ABC △BD AC ⊥AE BC AE BD DE CDE △2OD =OB 7a b +=2229a b +=()2a b -()()43267121x x x x ---÷+46x 2x 33x 33x ()21x +()4363x x +④把相减所得的差当作新的被除式,再按照上面的方法继续演算,直到余式为零或余式的次数低于除式的次数时为止.被除式=除式×商式+余式.若余式为零,说明这个多项式能被另一个多项式整除.余式为0,可以整除.请根据阅读材料,回答下列问题(直接填空):(1)请在两个方框内分别填入正确的数或式子;(2)多项式除以商式为______,余式为______;(3)多项式的一个因式是,则该多形式因式分解的结果为______.27.已知,,,连接和.(1)如图1,①求证:;②当时,的延长线交于点F ,写出与的数量关系并证明;(2)如图2,与的延长线交于点P ,连接,直接写出的度数(用含的式子表示)28.在平面直角坐标系,中,已知点,过点且垂直于x 轴的直线记为直线,过点且垂直于y 轴的直线记为直线.给出如下定义:将图形G 关于直线对称得到图形,再将图形关于直线得到图形,则称图形是图形G 关于点M 的双对称图形.(1)已知点M 的坐标为,点关于点M 的双对称图形点的坐标为______;()3210x x-- 432671x x x ∴---21x +2357x x +-2x +324839x x x +--1x -AB AC =AD AE =BAC DAE α∠=∠=BD CE BD CE =AD BD ⊥ED BC BF CF CE DB AP APB ∠αxOy (),M m n (),0m x m =()0,n y n =x m =1G 1G y n =2G 2G ()0,1()2,3N 2N(2)如图,的顶点坐标是,,.①已知点M 的坐标为,点,点,线段关于点M 的双对称图形线段位于内部(不含三角形的边),求n 的取值范围;②已知点M 的坐标为,直线l 经过点且平行于第一三象限的角平分线,当关于点M 的双对称图形与坐标轴有交点时,直线l 上存在满足条件的双对称图形上的点,直接写出k 的取值范围.北京二中教育集团2024—2025学年度第一学期初二数学期中考试参考答案一、选择题(共16分,每小题2分)1-5.ACADB 6-8.CBD二、填空题(共16分,每小题2分)9.12 10.11.三角形具有稳定性 12.121°13.和(和,和,和)14.24 15. 16.3.5三、解答题(共68分,其中第17-22题每题5分,第23-26题每题6分,第27-28题每题7分)17.原式18.原式19.原式20.解:原式当时 原式21.证明:, ABC △()2,3A -()4,1B -()0,1C ()1,1-()4,P n ()4,1Q n +PQ 22P Q ABC △(),3m m -+()0,k ABC △222A B C △222A B C △12x ≠ABF △DBF △ABD △AFD △BCD △AFD △ABE △DEF △()5,2--66698a a a=-=-()()()2224222y x yy x y x y =-=+-()222234211x x x x x =+-+=++=+2224129131210m m m m m =-+-+=-+2410m m --=31013=+=BE AC ⊥ AD BC ⊥90ADB ADC BEC ∴∠=∠=∠=︒, 在与中 22.(1)图略(2)线段垂直平分线上的点与线段两个端点距离相等 等边对等角23.解:(1)图略 (2)524.(1)等边三角形证:在等边中,,, 又为边上的中线 又 是等边三角形(2),,,为边上的中线, 在中, 25.解:(1)(2)9又 26.解:(1)2,(2),(3)27.解:(1)①证: 90EBC C ∴∠+∠=︒90DAC C ∠+∠=︒EBC DAC ∴∠=∠45ABC ∠=︒ 9045BAD ABC ∴∠=︒-∠=︒ABC BAD∴∠=∠AD BD ∴=BFD △ACD △ADB ADC BD ADEBC DAC ∠=∠⎧⎪=⎨⎪∠=∠⎩()ASA BFD ACD ∴≌△△BF AC∴=ABC △AB BC AC ==60C ABC BAC ∠=∠=∠=︒AB BC = BD AC ⊥12CD AC ∴=AE BC 12CE BC ∴=CD CE ∴=60C ∠=︒ CDE ∴△AB BC = AB AC =BD AC ⊥AE BC 1302ABD ABC ∴∠=∠=︒1302BAE CAE BAC ∠=∠=∠=︒ABD BAE ∴∠=∠OA OB ∴=BD AC ⊥ 90BDA ∴∠=︒ Rt AOD △30CAE ∠=︒24OA OD ∴==4OB OA ∴==()2222a b a ab b +=++7a b += ()249a b ∴+=()()()22222a b a b a b ++-=+ ()2229499a b ∴-=⨯-=32105x x--31x -5-()()2123x x -+BAC DAE α∠=∠= BAC CAD DAE CAD ∴∠+∠=∠+∠在与中 ②法1:延长至G ,使,连接。


2024-2025学年湖南省长沙市雅礼教育集团八年级(上)创新素养数学试卷一、填空题:本题共20小题,每小题4分,共80分。
1.因式分解:14m 2−13mn +19n 2= ______.2.计算:(1a−2+a)÷a 2−1a 2−2a −a a +1= ______.3.(a−2b +3c)(a +2b−3c)=______.4.已知x +y =5,xy =3,则x 2+5xy +y 2= ______.5.已知a 2+a−1=0,则a 3+2a 2+2024= ______.6.若a 2+b 2+4a−6b +13=0,则a b 的值为______.7.已知a 和b 互为倒数,a +b =4,求(a−b )2= ______.8.若(x +p)(x +q)=x 2+mx +36,且p ,q 为不大于10的正整数,则m = ______.9.求值:(2+1)×(22+1)×(24+1)×(28+1)×...×(264+1)= ______.10.若x 1×2+x 2×3+x 3×4+...+x 10×11=2011,则x = ______.11.如图,AB//CD ,点P 到AB 、BC 、CD 距离都相等,则∠P = ______.12.在△ABC 中,∠ABC 与∠ACB 的平分线相交于点F ,过点F 作DE//BC ,交AB 于点D ,交AC 于点E ,若BD +CE =9,则线段DE 之长为______.13.如图,△ABC 中,OD 、OE 分别是AB 、BC 边上的垂直平分线,OD 、OE 交于点O ,连接OA 、OC ,已知∠B =40°,则∠OAC =______°.14.等腰三角形一腰上的高与另一腰的夹角为40°,则这个三角形的顶角为______.15.在平面直角坐标系xOy 中,已知点A(2,3),在坐标轴上找一点P ,使得△AOP 是等腰三角形,则这样的点P 共有______个.16.如图,在△ABC 中,∠BAC =2∠C ,BD 为△ABC 的角平分线,BC =5,AB =3,则AD = ______.17.如图,正方形ABCD 中,点E 是BC 上一点,点F 是DC 上一点,∠EAF =45°,若BE =DF =1,则EF = ______.18.在Rt△ABC中,∠C=90°,AD平分∠CAB,AC=6,BC=8,CD=______.19.如图,AD是△ABC的平分线,DF⊥AB于点F,DE=DG,AG=16,AE=8,若S△ADG=64,则△DEF的面积为______.20.如图,等腰三角形ABC的底边BC长为6,面积是18,腰AC的垂直平分线EF分别交AC,AB于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则△CDM的周长的最小值为______.二、解答题:本题共4小题,共40分。


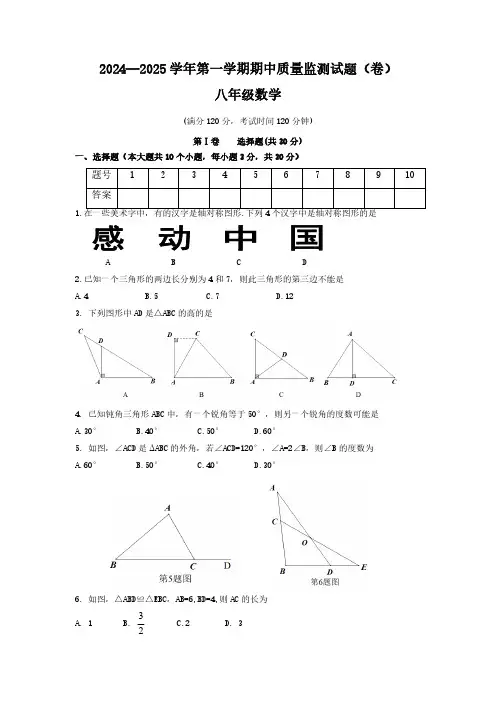
2024—2025学年第一学期期中质量监测试题(卷)八年级数学(满分120分,考试时间120分钟)第Ⅰ卷选择题(共30分)一、选择题(本大题共10个小题,每小题3分,共30分)题号12345678910答案1.在一些美术字中,有的汉字是轴对称图形.下列4个汉字中是轴对称图形的是A B C D2.已知一个三角形的两边长分别为4和7,则此三角形的第三边不能是A.4B.5C.7D.123. 下列图形中AD是△ABC的高的是4. 已知钝角三角形ABC中,有一个锐角等于50°,则另一个锐角的度数可能是A.30°B.40°C.50°D.60°5. 如图,∠ACD是ΔABC的外角,若∠ACD=120°,∠A=2∠B,则∠B的度数为A.60°B.50°C.40°D.30°6. 如图,△ABD≌△EBC,AB=6,BD=4,则AC的长为3A. 1B.C.2D. 327.在探索多边形内角和公式的过程中,多数同学采用如下表格中分割多边形的方法,并从四边形,五边形等特殊多边形的内角和计算,得到边形的内角和公式.多边形四边形五边形六边形七边形…边形图 例…内角和…以上表格中:由,,,,…,得到的结论,体现的数学思想是A. 数形结合B.类比C. 由特殊到一般D.公理化8. 如图,△ABC 与△A ′B ′C ′关于直线MN 对称,BB ′交MN 于点O ,则下列结论不一定正确的是A.∠ACB=∠A ′C ′B ′B.BO=B ′OC.AC ⊥B ′C ′D.AA ′∥ BB ′9.如图,点C 是∠AOB 的平分线上一点,CD ⊥OA ,CE ⊥OB ,垂足分别为点D ,E ,连接DE 交OC 于点F ,则下列结论中正确的个数为①CD=CE ;②DE ⊥OC ;③OD=OE ;④∠OCD=∠OCE ;⑤OF=2CFA. 2B. 3C. 4D. 510. 如图,在△ABC 中,BC 的垂直平分线分别交BC ,AB 于点D ,F.若△AFC 是等边三角形,AC=6,则DF 的长度为A.2B.3C. 4D. 6n n ︒=︒⨯-360180)24(︒=︒⨯-540180)25(︒=︒⨯-720180)26(︒=︒⨯-900180)27(︒⨯-180)2(n ︒=︒⨯-360180)24(︒=︒⨯-540180)25(︒=︒⨯-720180)26(︒=︒⨯-900180)27(︒⨯-180)2(n第Ⅱ卷 非选择题(共90分)二、填空题(本大题共5个小题,每小题3分,共15分)11. 如果一个正多边形的内角和为1620°,那么这个正多边形的一个外角的度数为 .12. A ,B 两点的坐标分别是(,)和(,4),并且A ,B 两点关于轴对称.则的值为 .13.如图,点B ,F ,C ,E 在同一条直线上,BF=CE ,AB ∥DE ,请添加一个条件,使△ABC ≌△DEF ,添加的条件可以是 .(填一个即可)14.如图,已知P 是射线ON 上一动点,∠AON=40°,当∠A=时,△AOP 为等腰三角形. 15.如图,AD 是△ABC 的中线,在AD 上取一点F ,连接BF 并延长交AC 于点E ,使AE=EF.若AC=5,AE=3,则BE 的长为 .三、解答题(本大题共8个小题,共75分)16.(6分)如图,已知△ABC ,请过点A 作一条直线,将△ABC 分成面积相等的两部分.(尺规作图,不写已知、求作、作法,只保留作图痕迹)a b c y b c a ++17.(8分)在如图所示的正方形网格中,以格点为顶点的三角形称为格点三角形,请按要求画出一个与△ABC关于某条直线对称的格点三角形.作图要求:①在四幅网格图中各画一个三角形;②所作三角形不能重复.18.(8分)如图,在△ABC中,AD⊥BC,垂足为D,BE平分∠ABC,交AD于点F,若∠BAC=70°,∠C=60°时,求∠AFB的度数19.(10分)如图,D,E是△ABC的边BC上两点,若BE=CD,∠ADB=∠AEC.求证:AB=AC.20.(10分)如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别为E,F,BE=CF.求证:AD是△ABC的角平分线.21.(10分)如图,点E是∠AOB的平分线上一点,∠MEN的两边分别与∠AOB的两边交于点M,N,且∠AOB+∠MEN=180°,EC⊥OA于点C,若△OEN和△OEM的面积分别为50和30.请求出△CEM的面积.22.(10分)如图,在等边△ABC 中,D 是AC 的中点,E 是BC 延长线上的一点,且CE=CD ,DM ⊥BC ,垂足为M.(1)求证:M 是BE 的中点;(2)若CM=2,求BE 的长度.23.(13分)综合探究:探索等腰三角形中相等的线段问题情境:数学活动课上,老师提出了一个问题:等腰三角形底边中点到两腰的距离相等吗?同学们就这个问题展开探究.问题初探:(1)希望小组的同学们根据题意画出了相应的图形,如图1.在△ABC 中,AB=AC ,D 是BC 的中点,DE ⊥AB ,DF ⊥AC ,垂足分别为点E ,F.经过合作,该小组的同学得出的结论是DE=DF.并且展示了他们的证法如下:证明:如图1,∵DE ⊥AB ,DF ⊥AC ,∴∠DEB=∠DFC=90°∵AB=AC ,∴∠B=∠C (依据1)∵D 是BC 的中点,∴BD=CD在△BDE 和△CDF 中∴△BDE ≌△CDF (依据2)∴DE=DF①请写出依据1和依据2的内容依据1: . 依据2: .⎪⎩⎪⎨⎧=∠=∠∠=∠CD BD CB DFCDEB②请你应用图2写出一种不同于希望小组的证法.问题再探:(2)未来小组的同学经过探究又有新的发现,如果在等腰三角形ABC中,作腰AB上的高CG,如图3.则CG与DE有确定的数量关系.请你直接写出这个数量关系为 .类比探究:(3)奋斗小组的同学认真研究过后,发现了以下两个正确结论:①在图4中,若DE,DF分别为△ABD和△ACD的中线,那么DE=DF仍然成立;②在图5中,若DE,DF分别为△ABD 和△ACD的角平分线,那么DE=DF仍然成立.请你选择其中一个结论,写出证明过程.2024—2025学年第一学期期中质量监测试题(卷)八年级数学答案一、选择题(本大题共10个小题,每小题3分,共30分)1—5 C D D A C 6—10 C C C C B二、填空题(本大题共5个小题,每小题3分,共15分)11. 12. 2 13. 答案不唯一,如AB=DE 14.40°或70°或100° 15. 8三、解答题(本大题共8个小题,共75分)16.(6分)图略17.(每图2分,共8分)参考答案如下:18.(8分)解:∵∠BAC=70°,∠C=60°∴∠ABC=50°………………………… 2分∵BE 平分∠ABC∴∠EBC=∠ABC=25°………………………… 4分 ∵AD ⊥BC∴∠FDB=90°………………………… 6分∴∠AFB=∠EBC+∠FDB=115°………………………… 8分19.(10分)证明:∵∠ADB=∠AEC∴∠ADE=∠AED………………………… 2分∴AD=AE………………………… 4分在△ABE 与△ACD 中………………………… 6分︒⎪⎭⎫ ⎝⎛1136021⎪⎩⎪⎨⎧=∠=∠=CD BE ADEAED AD AE∴△ABE ≌△ACD(SAS) ………………………… 8分∴AB=AC ………………………… 10分20.(10分)证明:∵D 是BC 的中点∴BD=CD………………………… 2分∵DE ⊥AB,DF ⊥AC∴∠BED=∠CFD=90° ………………………… 4分在Rt △BED 与Rt △CFD 中∴△BED ≌△CFD(HL) ……………………6分∴∠B=∠C ……………………7分∴AB=AC……………………8分∵D 是BC 的中点∴AD 是△ABC 的角平分线……………………10分21.(10分)解:过点E 作ED ⊥OB 于点D∴∠ODE=∠EDN=90°∵CE ⊥OA,OE 平分∠AOB∴∠OCE=90°,CE=DE………………………… 1分∴∠OCE=∠EDN∠AOB+∠CED=180°………………………… 2分∵∠AOB+∠MEN=180°∴∠CED=∠MEN………………………… 3分∴∠CED-∠MED=∠MEN-∠MED即∠CEM=∠DEN………………………… 4分在△CEM 和△DEN 中∴△CEM ≌△DEN(ASA)∴………………………… 5分⎩⎨⎧==CDBD CFBE ⎪⎩⎪⎨⎧∠=∠=∠=∠DEN CEM DE CE EDN OCE DEN CEM S S ∆∆=在Rt △COE 和Rt △DOE∴△COE ≌△DOE(HL)…………………………6 分∴………………………… 7分设∵∴∴………………………… 8分∵∴∴………………………… 9分∴………………………… 10分22.(第一问5分,第二问5分,共10分)证明:(1)连接BD ……………………… 1分 ∵△ABC 是等边三角形,D 是AC 的中点∴BD 平分∠ABC ,∠ABC=∠ACB=60°∴∠DBC=∠ABC=30° (2)分∵CE=CD∴∠E=∠CDE…………………………3分∴∠ACB=∠E+∠CDE∴∠E=30°∴∠E=∠DBC=30°…………………………4分∴BD=ED∵DM ⊥BE∴M 是BE 的中点…………………………5分(2)解:由(1)可知:⎩⎨⎧===OEOE DECE DOE COE S S ∆∆=xS S DEN CEM ==∆∆30=∆OEM S 30+=∆x S COE 30+=∆x S DOE 50=∆OEN S 5030=++x x 10=x 10=∆CEM S 21∠ACB=60°,M 是BE 的中点∵DM ⊥BE∴∠DME=90°…………………………6分∴∠CDM=30°∴CD=2CM…………………………7分∵CM=2∴CD=4∵CD=CE∴CE=4…………………………8分∴ME=CM+CE=6…………………………9分∵M 是BE 的中点∴BE=2ME=12…………………………10分23.(第一问6分,①各1分,②4分,第二问2分,第三问5分,共13分)(1)①依据1:等腰三角形的两个底角相等或等边对等角 ………………… 1分 依据2:两角分别相等且其中一组等角的对边相等的两个三角形全等或角角边或AAS ………………… 2分②(4分)答案不唯一,如连接AD ………………… 3分∵AB=AC,D 是BC 的中点∴AD 是∠BAC 的平分线 ………………… 5分∵DE ⊥AB,DF ⊥AC∴DE=DF ………………… 6分(2)(2分)CG=2DE …………………… 8分(3)(5分)选择①证明:∵DE ,DF 是△ABD 和△ACD 的中线∴BE=AB ,CF=AC ………………………… 9分 ∵AB=AC∴BE=CF,∠B=∠C ………………………… 10分又∵D 是BC 的中点∴BD=CD ………………………… 11分在△BDE 与△CDF 中2121⎪⎩⎪⎨⎧=∠=∠=CD BD CB CFBE∴△BDE ≌△CDF(SAS) ………………………… 12分∴DE=DF ………………………… 13分选择②证明:∵AB=AC,D 是BC 的中点∴∠B=∠C,BD=CD,AD ⊥BC∴∠ADB=∠ADC=90°………………………… 9分 又∵DE,DF 分别是△ABD 和△ACD 的平分线∴∠BDE=∠CDF=45°………………………… 10分 在△BDE 与△CDF 中∴△BDE ≌△CDF(ASA) ………………………… 12分 ∴DE=DF ………………………… 13分 ⎪⎩⎪⎨⎧∠=∠=∠=∠CDF BDE CDBD CB。


八年级数学《行知天下》答案2023 目录•第一章:数与代数– 1.1. 数的分类– 1.2. 小数的运算– 1.3. 算式的解法•第二章:几何– 2.1. 平面图形– 2.2. 三角形•第三章:数据统计– 3.1. 数据的收集和整理– 3.2. 数据的分析和应用第一章:数与代数1.1. 数的分类数的分类包括自然数、整数、有理数和无理数。
自然数包括正整数和零,整数包括正整数、负整数和零,有理数包括整数和分数,无理数是指不能表示为两个整数的比值的数。
在本章中,我们将学习如何判断一个数属于哪一种分类,并且学习各种分类数的运算法则。
1.2. 小数的运算小数运算是数学中的一个重要部分。
在这一节中,我们将学习如何进行小数的加减乘除运算,并解决与小数相关的实际问题。
1.3. 算式的解法算式是数学中常见的问题形式。
在这一节中,我们将学习如何解决各种类型的算式,包括整数算式、分数算式和小数算式。
我们将通过实例来演示解题的方法和技巧。
第二章:几何2.1. 平面图形平面图形是几何中的重要内容。
在这一节中,我们将学习各种平面图形的特性和性质,包括线段、角、三角形、四边形和圆等。
我们将学习如何计算平面图形的周长和面积,并解决与平面图形相关的实际问题。
2.2. 三角形三角形是几何中的基本形状。
在这一节中,我们将学习三角形的特性和判定方法,包括等边三角形、等腰三角形、直角三角形和一般三角形等。
我们将学习如何计算三角形的周长和面积,并解决与三角形相关的实际问题。
第三章:数据统计3.1. 数据的收集和整理数据统计是数学中的一项重要内容。
在这一节中,我们将学习如何收集和整理数据,包括数据的调查、数据的录入和数据的整理方法。
我们将学习如何使用图表来表示数据,并解决与数据统计相关的实际问题。
3.2. 数据的分析和应用数据分析是数据统计的核心内容。
在这一节中,我们将学习如何对收集到的数据进行分析和应用,包括数据的统计量、数据的概率和数据的推断等。
2024-2025学年八年级数学上学期第三次月考卷(浙教版)(考试时间:120分钟试卷满分:120分)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.测试范围:浙教版八上第1-4章,其中三角形初步14.1%,特殊三角形26.7%,不等式27.5%,坐标31.7%。
5.难度系数:0.65。
第一部分(选择题共30分)一、选择题:本题共10小题,每小题3分,共30分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知a<b,下列运用不等式基本性质变形不正确的是()A.a―3<b―3B.a+13<b+13C.3a<3b D.―3a<―3b【答案】D【详解】解:A、由a<b,可得a―3<b―3,原式变形正确,不符合题意;B、由a<b,可得a+13<b+13,原式变形正确,不符合题意;C、由a<b,可得3a<3b,原式变形正确,不符合题意;D、由a<b,可得―3a>―3b,原式变形错误,符合题意;故选:D.2.若y轴上的点P到x轴的距离为5,则点P为()A.(5,0)B.(5,0)或(―5,0)C.(0,5)D.(0,5)或(0,―5)【答案】D【详解】解:∵y轴上的点P到x轴的距离为5,∴当点P在y轴正半轴时,P(0,5);当点P在y轴负半轴时,P(0,―5);故选:D .3.如图,△ABC和△A′B′C′关于直线l对称,连接A A′,B B′,C C′,其中A A′与直线l交于点O,点D为直线l上一点,且不与点O重合,连接AD、A′D.下列说法错误的是( )A.∠ACB=∠A′C′B′B.线段A A′,B B′,C C′被直线l垂直平分C.△AD A′为等腰三角形D.线段AC、A′C′所在直线的交点不一定在直线l上【答案】D【详解】解:A、∵△ABC和△A′B′C′关于直线l对称,∴△ABC≌△A′B′C′,∴∠ACB=∠A′C′B′,正确,不符合题意;B、∵△ABC和△A′B′C′l对称,∴线段A A′,B B′,C C′被直线l垂直平分,正确,不符合题意;C、∵△ABC和△A′B′C′关于直线l对称,∴l是线段A A′的垂直平分线,∴△AD A′为等腰三角形,正确,不符合题意;D、∵△ABC和△A′B′C′关于直线l对称,∴线段AC、A′C′所在直线的交点一定在直线l上,原说法错误,符合题意.故选:D.4.如图,已知△ABC与△BDE全等,其中点D在边AB上,DE=AB,DE∥AC,AC=10,AD=3,则DE 的长是()A .7B .10C .13D .15【答案】C 【详解】解:∵DE ∥AC ,∴∠A =∠BDE ,∵△ABC 与△BDE 全等,DE =AB ,∴AC,BD 是对应边,∴AC =BD =10,∵AD =3,∴AB =AD +BD =13,∴DE =AB =13.故选:C5.如图,在△ABC 中,已知点D ,E ,F 分别为边BC ,AD ,CE 的中点,且S △ABC =32,则阴影部分面积是( )A .6B .4C .8D .10【答案】C 【详解】解:∵点D 为BC 中点,∴S △ABD =S △ACD =12S △ABC ,∵点E 为AD 中点,∴S △BDE =12S △ABD =14S △ABC ,S △CDE =12S △ACD =14S △ABC ,∴S △BCE =S △BDE +S △CDE =12S △ABC ,∵点F 为EC 中点,S △ABC =32,∴S △BEF =12S △BCE =12×12⋅S △ABC =12×12×32=8.故选:C .6.把不等式3x ―1≤2x +3的解集表示在数轴上,下列选项正确的是( )A .B .C .D .【答案】A【详解】解:3x ―1≤2x +3,3x ―2x ≤3+1,x ≤4.在数轴上表示为:故选:A .7.在平面直角坐标系中,将点A (m +1,n ―2)先向左平移2个单位长度,再向上平移4个单位长度得到点A ′. 若点A ′位于第二象限,则m ,n 的取值范围分别是( )A .m >1,n <―2B .m >1,n >―2C .m <1,n <―2D .m <1,n >―2【答案】D【详解】解:∵将点A(m +1,n ―2)先向左平移2个单位长度,再向上平移4个单位长度得到点A ′,∴A ′(m ―1,n +2),∵A ′(m ―1,n +2)在第二象限,∴m ―1<0,n +2>0,∴m <1,n >―2,故选:D .8.用长为 40 m 的铁丝围成如图所示的图形,一边靠墙,墙的长度 AC =30m ,要使靠墙的一边长不小于 25 m ,那么与墙垂直的一边长 x (m )的取值范围为( )A.0≤x≤5B.x≥103C.0≤x≤103D.103≤x≤5【答案】D【详解】根据题意和图形可得,25≤40―3x≤30解得:103≤x≤5,故选:D9.如图,面积为3的等腰△ABC,AB=AC,点B、点C在x轴上,且B(1,0)、C(3,0),规定把△ABC“先沿y轴翻折,再向下平移1个单位”为一次变换,这样连续经过2021次变换后,△ABC顶点A的坐标为()A.(―2,―2018)B.(2,―2018)C.(2,―2019)D.(―2,―2019)【答案】A【详解】解:∵面积为3的等腰△ABC,AB=AC,B(1,0)、C(3,0),∴点A到x轴的距离为3,横坐标为2,∴A(2,3),∴第1次变换A的坐标为(-2,2);第2次变换A的坐标为(2,1);第3次变换A的坐标为(-2,0);第4次变换A的坐标为(2,-1);第5次变换A的坐标为(-2,-2);∴第2021次变换后的三角形在x轴下方,且第三象限,∴点A的纵坐标为-2021+3=-2018,横坐标为-2,所以,连续经过2021次变换后,△ABC顶点A的坐标为(-2,-2018).故选:A.10.如图,等边△ABC中,AD为BC边上的高,点M、N分别在AD、AC上,且AM=CN,连BM、BN,当BM+BN最小时,则∠MBN=()A.15°B.30°C.45°D.60°【答案】B【详解】解:如图1中,作CH⊥BC,使得CH=BC,连接NH,BH.∵△ABC是等边三角形,AD⊥BC,CH⊥BC,∴∠DAC=∠DAB=30°,AD∥CH,∴∠HCN=∠CAD=∠BAM=30°,∵AM=CN,AB=BC=CH,∴△ABM≌△CHN,∴BM=HN,∵BN+HN≥BH,∴B,N,H共线时,BM+BN=NH+BN的值最小,如图2中,当B,N,H共线时,∵△ABM≌CHN,∴∠ABM=∠CHB=∠CBH=45°,∵∠ABD=60°,∴∠DBM=15°,∴∠MBN=45°―15°=30°,∴当BM+BN的值最小时,∠MBN=30°,故选:B.第二部分(非选择题共90分)二、填空题:本题共6小题,每小题3分,共18分。
2020-2021西安行知中学初二数学下期末试题(及答案)一、选择题1.若2(5)x -=x ﹣5,则x 的取值范围是( ) A .x <5B .x ≤5C .x ≥5D .x >52.当12a <<时,代数式2(2)1a a -+-的值为( ) A .1B .-1C .2a-3D .3-2a3.如图,矩形OABC 的顶点O 与平面直角坐标系的原点重合,点A ,C 分别在x 轴,y 轴上,点B 的坐标为(-5,4),点D 为边BC 上一点,连接OD ,若线段OD 绕点D 顺时针旋转90°后,点O 恰好落在AB 边上的点E 处,则点E 的坐标为( )A .(-5,3)B .(-5,4)C .(-5,52) D .(-5,2)4.要使函数y =(m ﹣2)x n ﹣1+n 是一次函数,应满足( ) A .m ≠2,n ≠2 B .m =2,n =2C .m ≠2,n =2D .m =2,n =05.下列说法:①四边相等的四边形一定是菱形②顺次连接矩形各边中点形成的四边形一定是正方形 ③对角线相等的四边形一定是矩形④经过平行四边形对角线交点的直线,一定能把平行四边形分成面积相等的两部分其中正确的有( )个. A .4B .3C .2D .16.对于函数y =2x +1下列结论不正确是( ) A .它的图象必过点(1,3) B .它的图象经过一、二、三象限 C .当x >12时,y >0 D .y 值随x 值的增大而增大7.如图2,四边形ABCD 的对角线AC 、BD 互相垂直,则下列条件能判定四边形ABCD 为菱形的是( )A .BA =BCB .AC 、BD 互相平分 C .AC =BD D .AB ∥CD8.若顺次连接四边形的各边中点所得的四边形是菱形,则该四边形一定是( )A .矩形B .一组对边相等,另一组对边平行的四边形C .对角线互相垂直的四边形D .对角线相等的四边形 9.若一个直角三角形的两边长为12、13,则第三边长为( )A .5B .17C .5或17D .5或10.如图,在▱ABCD 中,AB =6,BC =8,∠BCD 的平分线交AD 于点E ,交BA 的延长线于点F ,则AE +AF 的值等于( )A .2B .3C .4D .611.正方形具有而菱形不一定具有的性质是( ) A .对角线互相平分B .每条对角线平分一组对角C .对边相等D .对角线相等12.如图,函数y =ax +b 和y =kx 的图像交于点P ,关于x ,y 的方程组0y ax bkx y -=⎧⎨-=⎩的解是( )A .23x y =-⎧⎨=-⎩B .32x y =-⎧⎨=⎩C .32x y =⎧⎨=-⎩D .32x y =-⎧⎨=-⎩二、填空题13.如图,直线l 1:y =x +n –2与直线l 2:y =mx +n 相交于点P (1,2).则不等式mx +n <x +n –2的解集为______.14.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A 、B 、C 、E 的面积分别为2,5,1,10.则正方形D 的面积是______.15.已知20n 是整数,则正整数n 的最小值为___ 16.观察下列各式:221111++=1+1212⨯, 221111++=1+2323⨯, 221111++=1+3434⨯, ……请利用你所发现的规律,计算22111++12+22111++23+22111++34+…+22111++910,其结果为_______. 17.如图所示,已知Y ABCD 中,下列条件:①AC =BD ;②AB =AD ;③∠1=∠2;④AB ⊥BC 中,能说明Y ABCD 是矩形的有______________(填写序号)18.如图,矩形ABCD 的边AD 长为2,AB 长为1,点A 在数轴上对应的数是-1,以A 点为圆心,对角线AC 长为半径画弧,交数轴于点E ,则这个点E 表示的实数是_______19.如图,直线1y kx b =+过点A(0,2),且与直线2y mx =交于点P(1,m),则不等式组mx > +kx b > mx -2的解集是_________20.已知3a b +=,2ab =,则a bb a+的值为_________. 三、解答题21.某篮球队对队员进行定点投篮测试,每人每天投篮10次,现对甲、乙两名队员在五天中进球数(单位:个)进行统计,结果如下: 甲 10 6 10 6 8 乙79789经过计算,甲进球的平均数为8,方差为3.2. (1)求乙进球的平均数和方差;(2)如果综合考虑平均成绩和成绩稳定性两方面的因素,从甲、乙两名队员中选出一人去参加定点投篮比赛,应选谁?为什么?22.如图,已知一次函数y=kx+b 的图象经过A (﹣2,﹣1),B (1,3)两点,并且交x 轴于点C ,交y 轴于点D . (1)求该一次函数的解析式; (2)求△AOB 的面积.23.先化简再求值:(a ﹣22ab b a -)÷22a b a-,其中2,b=12.24.某公司开发出一款新的节能产品,该产品的成本价为6元件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试营销,售价为9元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的折线ODE 表示日销售量y (件)与销售时间x (天)之间的函数关系,已知线段DE 表示的函数关系中,时间每增加1天,日销售量减少(1)请直接写出y 与x 之间的函数关系式;(2)日销售利润不低于960元的天数共有多少天?试销售期间,日销售最大利润是多少元? (3)工作人员在统计的过程中发现,有连续两天的销售利润之和为1980元,请你算出是哪两天.25.已知:如图,在▱ABCD 中,设BA u u u r=a r,BC uuu r =b r. (1)填空:CA u u u r= (用a r、b r的式子表示)(2)在图中求作a r +b r.(不要求写出作法,只需写出结论即可)【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【解析】 【分析】2a (a≤0),由此性质求得答案即可. 【详解】 ()25x -,∴5-x≤0 ∴x≥5. 故选C . 【点睛】2a (a≥02a (a≤0).解析:A【解析】分析:首先由2a-=|a-2|,即可将原式化简,然后由1<a<2,去绝对值符号,继而(2)求得答案.详解:∵1<a<2,∴2a-=|a-2|=-(a-2),(2)|a-1|=a-1,∴2a-+|a-1|=-(a-2)+(a-1)=2-1=1.(2)故选A.点睛:此题考查了二次根式的性质与化简以及绝对值的性质,解答本题的关键在于熟练掌握二次根式的性质.3.A解析:A【解析】【分析】先判定△DBE≌△OCD,可得BD=OC=4,设AE=x,则BE=4﹣x=CD,依据BD+CD=5,可得4+4﹣x=5,进而得到AE=3,据此可得E(﹣5,3).【详解】由题可得:AO=BC=5,AB=CO=4,由旋转可得:DE=OD,∠EDO=90°.又∵∠B=∠OCD=90°,∴∠EDB+∠CDO=90°=∠COD+∠CDO,∴∠EDB=∠DOC,∴△DBE≌△OCD,∴BD=OC=4,设AE=x,则BE=4﹣x=CD.∵BD+CD=5,∴4+4﹣x=5,解得:x=3,∴AE=3,∴E(﹣5,3).故选A.【点睛】本题考查了全等三角形的判定与性质,矩形的性质以及旋转的性质的运用,解题时注意:全等三角形的对应边相等.4.C解析:C【解析】【分析】根据y=kx+b(k、b是常数,k≠0)是一次函数,可得m-2≠0,n-1=1,求解即可得答案.解:∵y=(m﹣2)x n﹣1+n是一次函数,∴m﹣2≠0,n﹣1=1,∴m≠2,n=2,故选C.【点睛】本题考查了一次函数,y=kx+b,k、b是常数,k≠0,x的次数等于1是解题关键.5.C解析:C【解析】【分析】【详解】∵四边相等的四边形一定是菱形,∴①正确;∵顺次连接矩形各边中点形成的四边形一定是菱形,∴②错误;∵对角线相等的平行四边形才是矩形,∴③错误;∵经过平行四边形对角线交点的直线,一定能把平行四边形分成面积相等的两部分,∴④正确;其中正确的有2个,故选C.考点:中点四边形;平行四边形的性质;菱形的判定;矩形的判定与性质;正方形的判定.6.C解析:C【解析】【分析】利用k、b的值依据函数的性质解答即可.【详解】解:当x=1时,y=3,故A选项正确,∵函数y=2x+1图象经过第一、二、三象限,y随x的增大而增大,∴B、D正确,∵y>0,∴2x+1>0,∴x>﹣12,∴C选项错误,故选:C.【点睛】此题考查一次函数的性质,熟记性质并运用解题是关键. 7.B【解析】【分析】【详解】解:对角线互相垂直平分的四边形为菱形.已知对角线AC、BD互相垂直,则需添加条件:AC、BD互相平分故选:B8.D解析:D【解析】【分析】如图,根据三角形的中位线定理得到EH∥FG,EH=FG,EF=12BD,则可得四边形EFGH是平行四边形,若平行四边形EFGH是菱形,则可有EF=EH,由此即可得到答案.【详解】如图,∵E,F,G,H分别是边AD,DC,CB,AB的中点,∴EH=12AC,EH∥AC,FG=12AC,FG∥AC,EF=12BD,∴EH∥FG,EH=FG,∴四边形EFGH是平行四边形,假设AC=BD,∵EH=12AC,EF=12BD,则EF=EH,∴平行四边形EFGH是菱形,即只有具备AC=BD即可推出四边形是菱形,故选D.【点睛】本题考查了中点四边形,涉及到菱形的判定,三角形的中位线定理,平行四边形的判定等知识,熟练掌握和灵活运用相关性质进行推理是解此题的关键.9.D解析:D【解析】【分析】根据告诉的两边长,利用勾股定理求出第三边即可.注意13,12可能是两条直角边也可能是一斜边和一直角边,所以得分两种情况讨论.【详解】当12,13为两条直角边时,第三边==,当13,12分别是斜边和一直角边时,第三边==5.故选D.【点睛】本题考查了勾股定理的知识,题目中渗透着分类讨论的数学思想.10.C解析:C【解析】【分析】【详解】解:∵四边形ABCD是平行四边形,∴AB∥CD,AD=BC=8,CD=AB=6,∴∠F=∠DCF,∵∠C平分线为CF,∴∠FCB=∠DCF,∴∠F=∠FCB,∴BF=BC=8,同理:DE=CD=6,∴AF=BF−AB=2,AE=AD−DE=2∴AE+AF=4故选C11.D解析:D【解析】【分析】列举出正方形具有而菱形不一定具有的所有性质,由此即可得出答案.【详解】正方形具有而菱形不一定具有的性质是:①正方形的对角线相等,而菱形不一定对角线相等;②正方形的四个角是直角,而菱形的四个角不一定是直角.故选D.【点睛】本题考查了正方形、菱形的性质,熟知正方形及菱形的性质是解决问题的关键.12.D解析:D【解析】【分析】根据两图象的交点坐标满足方程组,方程组的解就是交点坐标.【详解】由图可知,交点坐标为(﹣3,﹣2),所以方程组的解是32 xy=-⎧⎨=-⎩.故选D.【点睛】本题考查了函数解析式与图象的关系,满足解析式的点就在函数的图象上,在函数的图象上的点,就一定满足函数解析式.函数图象交点坐标为两函数解析式组成的方程组的解.二、填空题13.>1【解析】∵直线l1:y=x+n-2与直线l2:y=mx+n相交于点P(12)∴关于x的不等式mx+n<x+n-2的解集为x>1故答案为x>1解析:x>1【解析】∵直线l1:y=x+n-2与直线l2:y=mx+n相交于点P(1,2),∴关于x的不等式mx+n<x+n-2的解集为x>1,故答案为x>1.14.2【解析】【分析】设中间两个正方形和正方形D的面积分别为xyz然后有勾股定理解答即可【详解】解:设中间两个正方形和正方形D的面积分别为xyz则由勾股定理得:x=2+5=7;y=1+z;7+y=7+1解析:2【解析】【分析】设中间两个正方形和正方形D的面积分别为x,y,z,然后有勾股定理解答即可.【详解】解:设中间两个正方形和正方形D的面积分别为x,y,z,则由勾股定理得:x=2+5=7;y=1+z;7+y=7+1+z=10;即正方形D的面积为:z=2.故答案为:2.【点睛】本题考查了勾股定理的应用,掌握在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.15.5【解析】【分析】因为是整数且则5n是完全平方数满足条件的最小正整数n为5【详解】∵且是整数∴是整数即5n是完全平方数;∴n的最小正整数值为5故答案为:5【点睛】主要考查了二次根式的定义关键是根据乘解析:5【解析】【分析】,则5n是完全平方数,满足条件的最小正整数n为5.【详解】∴5n是完全平方数;∴n的最小正整数值为5.故答案为:5.【点睛】主要考查了二次根式的定义,关键是根据乘除法法则和二次根式有意义的条件.二次根式有意义的条件是被开方数是非负数进行解答.16.【解析】分析:直接根据已知数据变化规律进而将原式变形求出答案详解:由题意可得:+++…+=+1++1++…+1+=9+(1﹣+﹣+﹣+…+﹣)=9+=9故答案为9点睛:此题主要考查了数字变化规律正确解析:9 9 10【解析】分析:直接根据已知数据变化规律进而将原式变形求出答案.详解:由题意可得:=11+12⨯+1+123⨯+1+134⨯+ (1)1910⨯=9+(1﹣12+12﹣13+13﹣14+…+19﹣110)=9+9 10=99 10.故答案为99 10.点睛:此题主要考查了数字变化规律,正确将原式变形是解题关键.17.①④【解析】矩形的判定方法由:①有一个角是直角的平行四边形是矩形;②有三个角是直角的四边形是矩形;③对角线相等的平行四边形是矩形由此可得能使平行四边形ABCD 是矩形的条件是①和④解析:①④【解析】矩形的判定方法由:①有一个角是直角的平行四边形是矩形;②有三个角是直角的四边形是矩形;③对角线相等的平行四边形是矩形,由此可得能使平行四边形ABCD 是矩形的条件是①和④.18.—1【解析】【分析】首先根据勾股定理计算出AC 的长进而得到AE 的长再根据A 点表示-1可得E 点表示的数【详解】∵AD 长为2AB 长为1∴AC=∵A 点表示-1∴E 点表示的数为:-1故答案为-1【点睛】本题 解析:5—1 【解析】【分析】首先根据勾股定理计算出AC 的长,进而得到AE 的长,再根据A 点表示-1,可得E 点表示的数.【详解】∵AD 长为2,AB 长为1,∴AC=22215+=,∵A 点表示-1,∴E 点表示的数为:5-1,故答案为5-1.【点睛】本题主要考查了勾股定理的应用,关键是掌握勾股定理:在任何一个直角三角形中,两条直角边长的平方和一定等于斜边长的平方.19.【解析】【分析】【详解】解:由于直线过点A (02)P (1m )则解得故所求不等式组可化为:mx >(m-2)x+2>mx-20>-2x+2>-2解得:1<x <2 解析:12x <<【解析】【分析】【详解】解:由于直线过点A (0,2),P (1,m ), 则2k b m b +=⎧⎨=⎩,解得22k m b =-⎧⎨=⎩, 1(2)2y m x ∴=-+,故所求不等式组可化为:mx >(m-2)x+2>mx-2,0>-2x+2>-2,解得:1<x <2,20.【解析】【分析】先把二次根式进行化简然后把代入计算即可得到答案【详解】解:=∵∴原式=;故答案为:【点睛】本题考查了二次根式的混合运算以及二次根式的化简求值解题的关键是熟练掌握二次根式的混合运算的运【解析】【分析】先把二次根式进行化简,然后把3a b +=,2ab =,代入计算,即可得到答案.【详解】==(a b ab+, ∵3a b +=,2ab =,∴原式=3=22;故答案为:2. 【点睛】 本题考查了二次根式的混合运算,以及二次根式的化简求值,解题的关键是熟练掌握二次根式的混合运算的运算法则进行解题.三、解答题21.(1)乙平均数为8,方差为0.8;(2)乙.【解析】【分析】(1)根据平均数、方差的计算公式计算即可;(2)根据平均数相同时,方差越大,波动越大,成绩越不稳定;方差越小,波动越小,成绩越稳定进行解答.【详解】(1)乙进球的平均数为:(7+9+7+8+9)÷5=8,乙进球的方差为:15[(7﹣8)2+(9﹣8)2+(7﹣8)2+(8﹣8)2+(9﹣8)2]=0.8;(2)∵二人的平均数相同,而S 甲2=3.2,S 乙2=0.8,∴S 甲2>S 乙2,∴乙的波动较小,成绩更稳定,∴应选乙去参加定点投篮比赛.【点睛】本题考查了方差的定义:一般地设n 个数据,x 1,x 2,…x n 的平均数为x ,则方差S 21n=[(x 1x -)2+(x 2x -)2+…+(x n x -)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.也考查了平均数. 22.(1) y=43x+53;(2) 52. 【解析】【分析】(1)求经过已知两点坐标的直线解析式,一般是按待定系数法步骤求得;(2)△AOB 的面积=S △AOD +S △BOD ,因为点D 是在y 轴上,据其坐标特点可求出DO 的长,又因为已知A 、B 点的坐标则可分别求三角形S △AOD 与S △BOD 的面积.【详解】 解:(1)把A (﹣2,﹣1),B (1,3)代入y=kx+b 得213k b k b -+=-⎧⎨+=⎩, 解得4353k b ⎧=⎪⎪⎨⎪=⎪⎩.所以一次函数解析式为y=43x+53; (2)把x=0代入y=43x+53得y=53, 所以D 点坐标为(0,53), 所以△AOB 的面积=S △AOD +S △BOD =12×y=43x+53; ×2+12×y=43x+53×1=52. 【点睛】 本题考查了待定系数法求一次函数解析式.用待定系数法求一次函数的步骤:(1)设出函数关系式;(2)把已知条件(自变量与函数的对应值)代入函数关系式中,得到关于待定系数的方程(组).23.原式=a b a b-=+ 【解析】【分析】括号内先通分进行分式的加减运算,然后再进行分式的乘除法运算,最后将数个代入进行计算即可.【详解】 原式=()()222a ab b a a a b a b -+⨯+-=()()()2·a b aa ab a b-+-=a ba b -+,当,b=1时,原式.【点睛】本题考查了分式的化简求值,熟练掌握分式混合运算的运算顺序以及运算法则是解题的关键.24.(1)20(018)4432(1830)x xyx x<≤≤⎧=⎨-+≤⎩;(2)试销售期间,日销售最大利润是1080元;(3)连续两天的销售利润之和为1980元的是第16,17两天和第25,26两天.【解析】【分析】(1)根据点D的坐标利用待定系数法即可求出线段OD的函数关系式,根据第23天销售了340件,结合时间每增加1天日销售量减少4件,即可求出线段DE的函数关系式,联立两函数关系式求出交点D的坐标,此题得解;(2)分0≤x≤18和18<x≤30,找出关于x的一元一次不等式,解之即可得出x的取值范围,有起始和结束时间即可求出日销售利润不低于960元的天数,再根据点D的坐标结合日销售利润=单件利润×日销售数,即可求出日销售最大利润;(3) 设第x天和第(x+1)天的销售利润之和为1980元,据此列出方程,根据取值范围解答即可.【详解】(1)20(018),4432(1830).x xyx x≤≤⎧=⎨-+≤⎩<(2)当0≤x≤18时,根据题意得,(9﹣6)×20x≥960,解得:x≥16;当18<x≤30时,根据题意得,(9﹣6)×(-4x+432)≥960,解得:x≤28.∴16≤x≤28. 28-16+1=13(天),∴日销售利润不低于960元的天数共有13天.由20x=-4x+432解得,x=18,当x=18时,y=20x=360,∴点D的坐标为(18,360),∴日最大销售量为360件,360×(9-6)=1080(元),∴试销售期间,日销售最大利润是1080元.(3)设第x天和第(x+1)天的销售利润之和为1980元.∵1980÷(9﹣6)=660<340×2,∴x<17,或x+1>23,当x <17时,根据题意可得20x +20(x +1)=660,解得x =16,符合,当x +1>23时,-4x +432-4(x +1)+432=660,解得x =25,符合,∴连续两天的销售利润之和为1980元的是第16,17两天和第25,26两天.【点睛】本题考查了一次函数的应用、待定系数法一次函数解析式,解题的关键是利用待定系数法求出OD 的函数关系式以及依照数量关系找出DE 的函数关系式.25.(1) a r -b r ;(2) BD u u u r【解析】【分析】(1)根据三角形法则可知:,CA CB BA =+u u u v u u u v u u u v 延长即可解决问题;(2)连接BD .因为,BD BA AD =+u u u v u u u v u u u v ,AD BC =u u u v u u u v 即可推出.BD a b =+r u u u v r【详解】解:(1)∵,CA CB BA =+u u u v u u u v u u u v BA u u u v =a r ,BC uuu v =b r∴.CA a b =-r u u u v r故答案为a r -b r .(2)连接BD .∵,BD BA AD =+u u u v u u u v u u u v ,AD BC =u u u v u u u v ∴.BD a b =+r u u u v r∴BD u u u v 即为所求;【点睛】本题考查作图﹣复杂作图、平行四边形的性质、平面向量等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.。