小学五年级奥数第13课面积计算试题附答案-精品

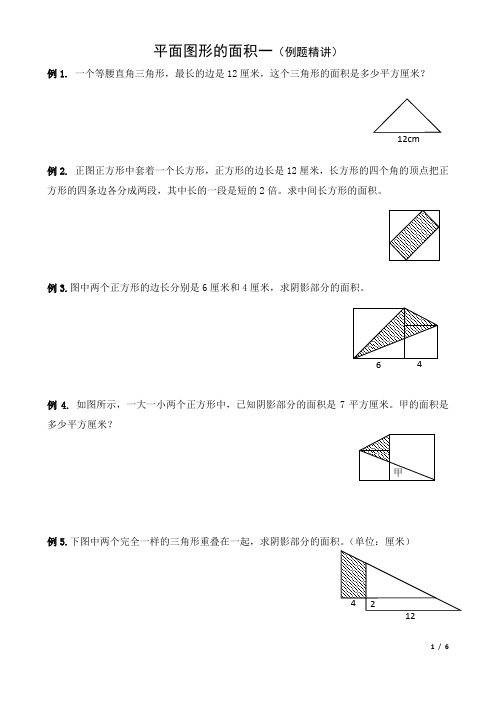
平面图形的面积一（例题精讲）例1. 一个等腰直角三角形，最长的边是12厘米，这个三角形的面积是多少平方厘米？例2. 正图正方形中套着一个长方形，正方形的边长是12厘米，长方形的四个角的顶点把正方形的四条边各分成两段，其中长的一段是短的2倍。

求中间长方形的面积。

例3.图中两个正方形的边长分别是6厘米和4厘米，求阴影部分的面积。

例4.如图所示，一大一小两个正方形中，已知阴影部分的面积是7平方厘米。

甲的面积是多少平方厘米？例5.下图中两个完全一样的三角形重叠在一起，求阴影部分的面积。

（单位：厘米）例6. 图中ABCD 是长方形，S 1比S 2的面积大6平方厘米，求EC 的长。

平面图形的面积一（课堂小测）7.求四边形ABCD 的面积。

（单位：厘米）8. 如下图长方形ABCD 的面积是16平方厘米，E 、F 都是所在边的中点，求三角形AEF 的面积。

9.右图中，正方形的边长4厘米，求长方形的面积。

10.如图，平行四边形BCEF 中，BC=8厘米，直角三角形中，AC=10厘米，阴影部分面积比甲的面积小8平方厘米。

平行四边形的高是多少厘米？A BCD 345°CD F CB DS 1A 4 6 S 2EE11.一个正方形的对角线长5厘米，这个正方形的面积是多少平方厘米？12.已知大正方形的边长是12厘米，求中间最小正方形的面积。

13.下图中，甲三角形的面积比乙三角形的面积大多少平方厘米？14.如图（单位：厘米）是两个相同的直角梯形重叠在一起，求阴影部分的面积。

15.如图所示，长方形的长12厘米，宽8厘米，A 、B 两点是长方形长和宽的中点，那么阴影部分的面积是多少？AB94 3 84 6乙甲5平面图形的面积二（例题精讲）例1. 一个等腰直角三角形，最长的边是12厘米，这个三角形的面积是多少平方厘米？12×12＝144（平方厘米） 144÷4＝36（平方厘米）例2. 正图正方形中套着一个长方形，正方形的边长是12厘米，长方形的四个角的顶点把正方形的四条边各分成两段，其中长的一段是短的2倍。

五年级奥数题：图形与面积一、填空题〔共10小题，每题3分，总分值30分〕1．〔3分〕如图是由16个同样大小的正方形组成的，如果这个图形的面积是400平方厘米，则它的周长是_________ 厘米．2．〔3分〕第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕，下面的图形中，每一小方格的面积是1．则7，2，1三个数字所占的面积之和是_________ ．3．〔3分〕如图中每一小方格的面积都是1平方厘米，则用粗线围成的图形面积是_________ 平方厘米．4．〔3分〕〔2014•模拟〕如图的两个正方形，边长分别为8厘米和4厘米，则阴影局部的面积是_________ 平方厘米．5．〔3分〕在△ABC中，BD=2DC，AE=BE，△ABC的面积是18平方厘米，则四边形AEDC的面积等于_________ 平方厘米．6．〔3分〕如图是边长为4厘米的正方形，AE=5厘米、OB是_________ 厘米．7．〔3分〕如图正方形ABCD的边长是4厘米，CG是3厘米，长方形DEFG的长DG是5厘米，则它的宽DE 是_________ 厘米．8．〔3分〕如图，一个矩形被分成10个小矩形，其中有6个小矩形的面积如下图，则这个大矩形的面积是_________ ．9．〔3分〕如图，正方形ABCD的边长为12，P是边AB上的任意一点，M、N、I、H分别是边BC、AD上的三等分点，E、F、G是边CD上的四等分点，图中阴影局部的面积是_________ ．10．〔3分〕图中的长方形的长和宽分别是6厘米和4厘米，阴影局部的总面积是10平方厘米，四边形ABCD 的面积是_________ 平方厘米．二、解答题〔共4小题，总分值0分〕11．图中正六边形ABCDEF的面积是54．AP=2PF，CQ=2BQ，求阴影四边形CEPQ的面积．12．如图，涂阴影局部的小正六角星形面积是16平方厘米．问：大正六角星形面积是多少平方厘米．13．一个周长是56厘米的大长方形，按图中〔1〕与〔2〕所示意那样，划分为四个小长方形．在〔1〕中小长方形面积的比是：A：B=1：2，B：C=1：2．而在〔2〕中相应的比例是A'：B'=1：3，B'：C'=1：3．又知，长方形D'的宽减去D的宽所得到的差，与D'的长减去在D的长所得到的差之比为1：3．求大长方形的面积．14．〔2012•模拟〕如图，CD=5，DE=7，EF=15，FG=6，直线AB将图形分成两局部，左边局部面积是38，右边局部面积是65，则三角形ADG的面积是_________ ．2010年五年级奥数题：图形与面积〔B〕参考答案与试题解析一、填空题〔共10小题，每题3分，总分值30分〕1．〔3分〕如图是由16个同样大小的正方形组成的，如果这个图形的面积是400平方厘米，则它的周长是170 厘米．考点：巧算周长．分析：要求该图形的周长，先求出每个小正方形的面积，根据正方形的面积公式，得出小正方形的边长，然后先算出该图形的外周的长，因为、外的长相等，再乘2即可得出结论．解答：解：400÷16=25〔平方厘米〕，因为5×5=25〔平方厘米〕，所以每个小正方形的边长为5厘米，周长为：〔5×4+5×4+5×3+5×2+5×3+5〕×2，=85×2，=170〔厘米〕；答：它的周长是170厘米．点评：此类题解答的关键是先求出每个小正方形的面积，根据正方形的面积公式，得出小正方形的边长，进而算出该图形的外周的长，因为、外的长相等，再乘2即可得出结论．2．〔3分〕第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕，下面的图形中，每一小方格的面积是1．则7，2，1三个数字所占的面积之和是25 ．考点：组合图形的面积．分析：此题需要进展图形分解："7〞分成一个长方形、一个等腰直角三角形、一个平行四边形；"2〞分成一个梯形、一个平行四边形、一个长方形；"1〞分成一个梯形和两个长方形．然后进展图形转换，依据题目条件即可求出结果．解答：解："7〞所占的面积和=+3+4=，"2〞所占的面积和=3+4+3=10，"1〞所占的面积和=+7=，则7，2，1三个数字所占的面积之和=++10=25．故答案为：25．点评：此题关键是进展图形分解和转换．3．〔3分〕如图中每一小方格的面积都是1平方厘米，则用粗线围成的图形面积是 6.5 平方厘米．考点：组合图形的面积．分析：由图可以观察出：大正方形的面积减粗线以外的图形面积即为粗线围成的图形面积．解答：解：大正方形的面积为4×4=16〔平方厘米〕；粗线以外的图形面积为：整格有3个，左上，右上，右中，右下，左中，右中，共有3++5×=9.5〔平方厘米〕；所以粗线围成的图形面积为16﹣9.5=6.5〔平方厘米〕；答：粗线围成的图形面积是6.5平方厘米．故此题答案为：6.5．点评：此题关键是对图形进展合理地割补．4．〔3分〕〔2014•模拟〕如图的两个正方形，边长分别为8厘米和4厘米，则阴影局部的面积是24 平方厘米．考点：组合图形的面积．分析：两个正方形的面积减去两个空白三角形的面积．解答：解：4×4+8×8﹣×4×〔4+8〕﹣×8×8，=16+64﹣24﹣32，=24〔cm2〕；答：阴影的面积是24cm2．故答案为：24．点评：求组合图形面积的化为求常用图形面积的和与差求解．5．〔3分〕在△ABC中，BD=2DC，AE=BE，△ABC的面积是18平方厘米，则四边形AEDC的面积等于12 平方厘米．考点：相似三角形的性质〔份数、比例〕；三角形的周长和面积．分析：根据题意，连接AD，即可知道△ABD和△ADC的关系，△ADE和△BDE的关系，由此即可求出四边形AEDC的面积．解答：解：连接AD，因为BD=2DC，所以，S△ABD=2S△ADC，即，S△ABD=18×=12〔平方厘米〕，又因为，AE=BE，所以，S△ADE=S△BDE，即，S△BDE=12×=6〔平方厘米〕，所以AEDC的面积是：18﹣6=12〔平方厘米〕；故答案为：12．点评：解答此题的关键是，根据题意，添加辅助线，帮助我们找到三角形之间的关系，由此即可解答．6．〔3分〕如图是边长为4厘米的正方形，AE=5厘米、OB是 3.2 厘米．考点：组合图形的面积．分析：连接BE、AF可以看出，三角形ABE的面积是正方形面积的一半，再依据三角形面积公式就可以求出OB 的长度．解答：解：如图连接BE、AF，则BE与AF相交于D点S△ADE=S△BDF则S△ABE=S正方形=×〔4×4〕=8〔平方厘米〕；OB=8×2÷5=3.2〔厘米〕；答：OB是3.2厘米．故答案为：3.2．点评：此题主要考察三角形和正方形的面积公式，将数据代入公式即可．7．〔3分〕如图正方形ABCD的边长是4厘米，CG是3厘米，长方形DEFG的长DG是5厘米，则它的宽DE 是 3.2 厘米．考点：组合图形的面积．分析：连接AG，则可以依据题目条件求出三角形AGD的面积，因为DG，进而可以求三角形AGD的高，也就是长方形的宽，问题得解．解答：解：如图连接AGS△AGD=S正方形ABCD﹣S△CDG﹣S△ABG，=4×4﹣3×4÷2﹣1×4÷2=16﹣6﹣2=8〔平方厘米〕；8×2÷5=3.2〔厘米〕；答：长方形的宽是3.2厘米．故答案为：3.2．点评：依据题目条件做出适宜的辅助线，问题得解．8．〔3分〕如图，一个矩形被分成10个小矩形，其中有6个小矩形的面积如下图，则这个大矩形的面积是243 ．考点：组合图形的面积．分析：从图中可以看出每上、下两个小矩形的一个边是相邻的，也就是说长是相等的，则根据矩形的面积公式知，如果长一样，面积之比也就是宽之比，反之宽之比也就是面积之比；由中间面积20和16的矩形，可以算出空着的小矩形面积，最后把所有小矩形面积加起来就是大矩形的面积．解答：解：由图和题意知，中间上、下小矩形的面积比是：20：16=5：4，所以宽之比是5：4，则，A：36=5：4得A=45；25：B=5：4得B=20；30：C=5：4得C=24；D：12=5：4得D=15；所以大矩形的面积=45+36+25+20+20+16+30+24+15+12=243；故答案为：243．点评：此题考察了如果长方形的长一样，宽之比等于面积之比，还考察了比例的有关知识．9．〔3分〕如图，正方形ABCD的边长为12，P是边AB上的任意一点，M、N、I、H分别是边BC、AD上的三等分点，E、F、G是边CD上的四等分点，图中阴影局部的面积是60 ．考点：组合图形的面积．分析：根据题意：正方形ABCD的边长为12，P是边AB上的任意一点，M、N、I、H分别是边BC、AD上的三等分点，E、F、G是边CD上的四等分点，可连接DP，然后再利用三角形的面积公式进展计算即可得到答案．解答：解：阴影局部的面积=×DH×AP+×DG×AD+×EF×AD+×MN×BP=×4×AP+×3×12+×3×12+×4×BP=2AP+18+18+2BP=36+2×〔AP+BP〕=36+2×12=36+24=60．答：这个图形阴影局部的面积是60．点评：此题主要考察的是三角形的面积公式．10．〔3分〕图中的长方形的长和宽分别是6厘米和4厘米，阴影局部的总面积是10平方厘米，四边形ABCD 的面积是 4 平方厘米．考点：重叠问题；三角形的周长和面积．分析：因为S△EFC+S△GHC=四边形EFGH面积÷2=12，S△AEF+S△AGH=四边形EFGH面积÷2=12，所以S△ABE+S△ADH=S△BFC+S△DGC=四边形EFGH面积÷2﹣阴影局部的总面积是10平方厘米=2平方厘米．所以：四边形ABCD面积=S△ECH﹣〔S△ABE+S△ADH〕=四边形ABCD面积÷4﹣2=6﹣2=4平方厘米．解答：解：由题意推出：S△ABE+S△ADH=S△BFC+S△DGC=四边形EFGH面积÷2﹣阴影面积10平方厘米=2平方厘米．所以：四边形ABCD面积=S△ECH﹣〔S△ABE+S△ADH〕=四边形ABCD面积÷4﹣2=6﹣2=4平方厘米．故答案为：4．点评：此题在重叠问题中考察了三角形的周长和面积公式，此题设计的非常精彩．二、解答题〔共4小题，总分值0分〕11．图中正六边形ABCDEF的面积是54．AP=2PF，CQ=2BQ，求阴影四边形CEPQ的面积．考点：等积变形〔位移、割补〕．分析：如图，将正六边形ABCDEF等分为54个小正三角形，根据平行四边形对角线平分平行四边形面积，采用数小三角形的方法来计算面积．解答：解：如图，S△PEF=3，S△CDE=9，S四边形ABQP=11．上述三块面积之和为3+9+11=23．因此，阴影四边形CEPQ面积为54﹣23=31．点评：此题主要利用面积分割，用数根本小三角形面积来解决问题．12．如图，涂阴影局部的小正六角星形面积是16平方厘米．问：大正六角星形面积是多少平方厘米．考点：等积变形〔位移、割补〕．分析：由图及题意知，可把涂阴影局部小正六角星形等分成12个小三角形，且都与外围的6个空白小三角形面积相等，涂阴影局部的小正六角星形面积是16平方厘米，可求出大正六角星形中心正六边形的面积，而这个正六边形又可等分成6个小正三角形，且它们与外围六个大角的面积相等，进而可求出大正六角星形面积解答：解：如下列图所示，涂阴影局部小正六角星形可等分成12个小三角形，且都与外围的6个空白小三角形面积相等，所以正六边形ABCDEF的面积：16÷12×〔12+6〕=24〔平方厘米〕；又由于正六边形ABCDEF又可等分成6个小正三角形，且它们与外围六个大角的面积相等，所以大正六角星形面积：24×2=48〔平方厘米〕；答：大正六角星形面积是48平方厘米．点评：此题要借助求正六边形的面积来解答，它既可看作是18个小正三角形，又可看作是6个大点的正三角形组成．13．一个周长是56厘米的大长方形，按图中〔1〕与〔2〕所示意那样，划分为四个小长方形．在〔1〕中小长方形面积的比是：A：B=1：2，B：C=1：2．而在〔2〕中相应的比例是A'：B'=1：3，B'：C'=1：3．又知，长方形D'的宽减去D的宽所得到的差，与D'的长减去在D的长所得到的差之比为1：3．求大长方形的面积．考点：比的应用；图形划分．分析：要求大长方形的面积，需求出它的长和宽，由条件"在〔1〕中小长方形面积的比是：A：B=1：2，B：C=1：2．而在〔2〕中相应的比例是A'：B'=1：3，B'：C'=1：3．又知，长方形D'的宽减去D的宽所得到的差，与D'的长减去在D的长所得到的差之比为1：3〞可知：D的宽是大长方形宽的，D′的宽是大长方形宽的，D的长是×〔28﹣大长方形的宽〕，D′的长是×〔28﹣大长方形的宽〕，由此便可以列式计算．解答：解：设大长方形的宽为*，则长为28﹣*因为D的宽=*，D′的宽=*，所以，D′的宽﹣D的宽=．D长=×〔28﹣*〕，D′长=×〔28﹣*〕，D′长﹣D长=×〔28﹣*〕，由题设可知：=即=，于是=，*=8．于是，大长方形的长=28﹣8=20，从而大长方形的面积为8×20=160平方厘米．答：大长方形的面积是160平方米．点评：此题比拟复杂，主要考察比的关系，应利用比的意义，找清数量见的比，再利用题目条件，就可以进展计算求得结果．14．〔2012•模拟〕如图，CD=5，DE=7，EF=15，FG=6，直线AB将图形分成两局部，左边局部面积是38，右边局部面积是65，则三角形ADG的面积是40 ．考点：三角形的周长和面积．分析：可以把S△ADE看成是一个整体，根据各线段的关系和左右两局部面积的关系，可以列出一个方程，求出S△ADE的面积，然后再根据所求三角形与S△ADE的关系求出答案．解答：解：由题意知，S=3S△ADE，S△BFE=S△BEC，△AEG设S△ADE=*，则S△AEG=3*，S△BFE=〔38﹣*〕，可列出方程：〔38﹣*〕+3*=65，解方程，得：*=10，所以S△ADG=10×〔1+3〕=40．故答案为：40．点评：此题考察了如何利用边的关系求三角形的面积．。

五年级数学奥数题面积题
【原创版】
目录
1.题目概述
2.题目解析
3.解题思路
4.解答过程
5.题目答案
正文
1.题目概述
这是一道针对五年级学生的数学奥数题，主要考察学生对面积知识的理解和运用。

题目内容为一个长方形的长为 10 厘米，宽为 6 厘米，求这个长方形的面积。

2.题目解析
长方形的面积计算公式为：面积 = 长×宽。

根据题目所给的数据，长方形的长为 10 厘米，宽为 6 厘米，所以可以通过公式计算出它的面积。

3.解题思路
首先，要明确题目所求的是长方形的面积，根据公式，面积等于长乘以宽。

然后，将题目中给出的长和宽代入公式进行计算。

4.解答过程
根据公式，长方形的面积 = 长×宽，将题目中给出的长和宽代入公式，得到：
面积 = 10 厘米× 6 厘米 = 60 平方厘米
所以，这个长方形的面积是 60 平方厘米。

5.题目答案
这道题目的答案是 60 平方厘米。

五年级奥数题：图形与面积一、填空题（共10小题，每小题3分，满分30分）1．（3分）如图是由16个同样大小的正方形组成的，如果这个图形的面积是400平方厘米，那么它的周长是_________厘米．2．（3分）第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕，下面的图形中，每一小方格的面积是1．那么7，2，1三个数字所占的面积之和是_________．3．（3分）如图中每一小方格的面积都是1平方厘米，那么用粗线围成的图形面积是_________平方厘米．4．（3分）（2014?长沙模拟）如图的两个正方形，边长分别为8厘米和4厘米，那么阴影部分的面积是_________平方厘米．5．（3分）在△ABC中，BD=2DC，AE=BE，已知△ABC的面积是18平方厘米，则四边形AEDC 的面积等于_________平方厘米．6．（3分）如图是边长为4厘米的正方形，AE=5厘米、OB是_________ 厘米．7．（3分）如图正方形ABCD的边长是4厘米，CG是3厘米，长方形DEFG的长DG是5厘米，那么它的宽DE是_________厘米．8．（3分）如图，一个矩形被分成10个小矩形，其中有6个小矩形的面积如图所示，那么这个大矩形的面积是_________．9．（3分）如图，正方形ABCD的边长为12，P是边AB上的任意一点，M、N、I、H分别是边BC、AD上的三等分点，E、F、G是边CD上的四等分点，图中阴影部分的面积是_________．10．（3分）图中的长方形的长和宽分别是6厘米和4厘米，阴影部分的总面积是10平方厘米，四边形ABCD的面积是_________平方厘米．二、解答题（共4小题，满分0分）11．图中正六边形ABCDEF的面积是54．AP=2PF，CQ=2BQ，求阴影四边形CEPQ的面积．2 / 1012．如图，涂阴影部分的小正六角星形面积是16平方厘米．问：大正六角星形面积是多少平方厘米．13．一个周长是56厘米的大长方形，按图中（1）与（2）所示意那样，划分为四个小长方形．在（1）中小长方形面积的比是：A：B=1：2，B：C=1：2．而在（2）中相应的比例是A'：B'=1：3，B'：C'=1：3．又知，长方形D'的宽减去D的宽所得到的差，与D'的长减去在D的长所得到的差之比为1：3．求大长方形的面积．14．（2012?武汉模拟）如图，已知CD=5，DE=7，EF=15，FG=6，直线AB将图形分成两部分，左边部分面积是38，右边部分面积是65，那么三角形ADG的面积是_________．3 / 102010年五年级奥数题：图形与面积（B）参考答案与试题解析一、填空题（共10小题，每小题3分，满分30分）1．（3分）如图是由16个同样大小的正方形组成的，如果这个图形的面积是400平方厘米，那么它的周长是170厘米．考点：巧算周长．分析：要求该图形的周长，先求出每个小正方形的面积，根据正方形的面积公式，得出小正方形的边长，然后先算出该图形的外周的长，因为内、外的长相等，再乘2即可得出结论．解答：解：400÷16=25（平方厘米），因为5×5=25（平方厘米），所以每个小正方形的边长为5厘米，周长为：（5×4+5×4+5×3+5×2+5×3+5）×2，=85×2，=170（厘米）；答：它的周长是170厘米．点评：此类题解答的关键是先求出每个小正方形的面积，根据正方形的面积公式，得出小正方形的边长，进而算出该图形的外周的长，因为内、外的长相等，再乘2即可得出结论．2．（3分）第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕，下面的图形中，每一小方格的面积是1．那么7，2，1三个数字所占的面积之和是25．考点：组合图形的面积．分析：此题需要进行图形分解：“7”分成一个长方形、一个等腰直角三角形、一个平行四边形；“2”分成一个梯形、一个平行四边形、一个长方形；“1”分成一个梯形和两个长方形．然后进行图形转换，依据题目条件即可求出结果．解答：解：“7”所占的面积和=+3+4=，“2”所占的面积和=3+4+3=10，“1”所占的面积和=+7=，++10=25．那么7，2，1三个数字所占的面积之和=故答案为：25．点评：此题关键是进行图形分解和转换．3．（3分）如图中每一小方格的面积都是1平方厘米，那么用粗线围成的图形面积是6.5平方厘米．4 / 10组合图形的面积考由图可以观察出：大正方形的面积减粗线以外的图形面积即为粗线围成的图形面积分析（平方厘米解：大正方形的面积4=1解答=9.53++5×左中3个，左上，右上，右中，右下，，右中，共有粗线以外的图形面积为：整格有（平方厘米）；（平方厘米）；﹣所以粗线围成的图形面积为169.5=6.5 6.5平方厘米．答：粗线围成的图形面积是 6.5．故此题答案为：此题关键是对图形进行合理地割补．点评：平方厘米，那么阴影部分的面积是分）（2014?长沙模拟）如图的两个正方形，边长分别为8厘米和4244．（3厘米．考点：组合图形的面积．分析：两个正方形的面积减去两个空白三角形的面积．解答：8，）﹣4+8×8××解：4×4+88﹣×4×（，﹣24﹣32=16+642；cm）（=242．答：阴影的面积是24cm 24．故答案为：求组合图形面积的化为求常用图形面积的和与差求解．点评：12的面积等于的面积是△ABC18平方厘米，则四边形AEDCAE=BEABC35．（分）在△中，BD=2DC，，已知平方厘米．相似三角形的性质（份数、比例）；三角形的周长和面积．考点：的关系，由此即可求出四边形BDE△的关系，ABD根据题意，连接分析：AD，即可知道△和△ADC△ADE和的面积．AEDC 解答：，，因为BD=2DC解：连接AD ABD=2S△ADC，△所以，S△即，SABD=18（平方厘米）=12，×又因为，AE=BE，5 / 10ADE=BD所以S=6（平方厘米），即，S△BDE=12×6=12（平方厘米）；所以AEDC的面积是：18﹣故答案为：12．点评：解答此题的关键是，根据题意，添加辅助线，帮助我们找到三角形之间的关系，由此即可解答．厘米．厘米、OB是3.26．（3分）如图是边长为4厘米的正方形，AE=5组合图形的面积考O的面积是正方形面积的一半，再依据三角形面积公式就可以求A可以看出，三角AB连分析B的长度A相交解：如图连BA，B解答：BDF△S△ADE=S 则=8（平方厘米）；（4×4）×S△ABE=S正方形= （厘米）；OB=8×2÷5=3.2 3.2厘米．答：OB 是．故答案为：3.2 此题主要考查三角形和正方形的面积公式，将数据代入公式即可．点评：DE5厘米，那么它的宽厘米，长方形DEFG的长DG是34 ．7（3分）如图正方形ABCD的边长是厘米，CG是厘米．是 3.2：组合图形的面积．考点的高，DG的面积，因为已知，进而可以求三角形AGDAGDAG 分析：连接，则可以依据题目条件求出三角形也就是长方形的宽，问题得解．AG解答：解：如图连接6 / 10S，=S﹣S﹣S ABGCDG△△△AGDABCD正方形2 4÷2﹣1××4﹣3×4÷=426﹣=16﹣（平方厘米）；=8 （厘米）；2÷5=3.28×3.2厘米．答：长方形的宽是3.2．故答案为：依据题目条件做出合适的辅助线，问题得解．点评：．24310个小矩形，其中有6个小矩形的面积如图所示，那么这个大矩形的面积是8．（3分）如图，一个矩形被分成组合图形的面积．考点：从图中可以看出每上、下两个小矩形的一个边是相邻的，也就是说长是相等的，那么根据矩形的面积公式分析：的矩形，可16知，如果长相同，面积之比也就是宽之比，反之宽之比也就是面积之比；由中间面积20和以算出空着的小矩形面积，最后把所有小矩形面积加起来就是大矩形的面积．解：由图和题意知，解答：，：4中间上、下小矩形的面积比是：20：16=5 ，：4所以宽之比是5 A=45；得：36=5：4那么，A B=20；B=5：4得25：C=24；C=5：4得30：D=15；：4得D：12=5 ；=45+36+25+20+20+16+30+24+15+12=243所以大矩形的面积．故答案为：243 此题考查了如果长方形的长相同，宽之比等于面积之比，还考查了比例的有关知识．点评：上的三等、AD、IH分别是边BC是边12，PAB上的任意一点，M、N、的边长为（9．3分）如图，正方形ABCD ．上的四等分点，图中阴影部分的面积是60E分点，、F、G是边CD组合图形的面积．考点：上的三ADBC、HN上的任意一点，M、、I、分别是边ABP12ABCD 分析：根据题意：正方形的边长为，是边，然后再利用三角形的面积公式进行计算即可得到答DP上的四等分点，可连接是边、、等分点，EFGCD 案．7 / 10 解答BPMAPDADEAD解：阴影部分的面D×BP4×××3×12+=×4×AP+×3×12+=2AP+18+18+2BPAP+BP）=36+2×（12 =36+2×=36+24=60．．答：这个图形阴影部分的面积是60 此题主要考查的是三角形的面积公式．点评：的厘米，阴影部分的总面积是10平方厘米，四边形ABCD分）10．（3 图中的长方形的长和宽分别是6厘米和4 4平方厘米．面积是：重叠问题；三角形的周长和面积．考点，2=12÷2=12，S△AEF+S△AGH=四边形EFGH 面积÷GHC=分析：因为S△EFC+S△四边形EFGH面积平方÷△DGC=四边形EFGH面积2﹣阴影部分的总面积是10平方厘米=2ADH=S所以S△ABE+S△△BFC+S 厘米．2=4平方厘米．﹣÷4﹣2=6=ECH所以：四边形ABCD面积=S△﹣（S△ABE+S△ADH）四边形ABCD面积平﹣阴影面积10平方厘米=2DGC=S解答：解：由题意推出：△ABE+S△ADH=S △BFC+S△四边形EFGH面积÷2 方厘米．﹣）=四边形ABCD面积÷42=6﹣2=4平方厘米．ADHS=S所以：四边形ABCD面积△ECH﹣（△ABE+S△故答案为：4．此题在重叠问题中考查了三角形的周长和面积公式，此题设计的非常精彩．点评：0分）二、解答题（共4小题，满分的面CQ=2BQ，求阴影四边形CEPQAP=2PFABCDEF11．图中正六边形的面积是54．，积．．考点：等积变形（位移、割补）个小正三角形，根据平行四边形对角线平分平行四边形面积，采用分析：54ABCDEF等分为如图，将正六边形数小三角形的办法来计算面积．解答：解：如图，PEF=3S△，S，CDE=9S△四边形ABQP=11．8 / 1023=3．因此，阴影四边CEP面积5上述三块面积之和3+9+11=2此题主要利用面积分割，用数基本小三角形面积来解决问题点评平方厘米．问：大正六角星形面积是多少平方厘米．．如图，涂阴影部分的小正六角星形面积是1612等积变形（位移、割补考个空白小三角形面个小三角形，且都与外围分析由图及题意知，可把涂阴影部分小正六角星形等分1平方厘米，可求出大正六角星形中心正六边形的面积，相等，已知涂阴影部分的小正六角星形面积1个小正三角形，且它们与外围六个大角的面积相等，进而可求出大正六角星这个正六边形又可等分面解：如下图所示解答：6个空白小三角形面积相等，涂阴影部分小正六角星形可等分成12个小三角形，且都与外围的（平方厘米）；12+6）=24×所以正六边形ABCDEF的面积：16÷12（6个小正三角形，且它们与外围六个大角的面积相等，又由于正六边形ABCDEF又可等分成（平方厘米）；24×2=48所以大正六角星形面积：48平方厘米．答：大正六角星形面积是个大点的正三角形组个小正三角形，又可看作是6 此题要借助求正六边形的面积来解答，它既可看作是18点评：成．）中小长方形1）与（2）所示意那样，划分为四个小长方形．在（13．一个周长是56厘米的大长方形，按图中（1D'．又知，长方形：33，B'：C'=1）中相应的比例是：C=1：2．而在（2A'：B'=1：B面积的比是：A：B=1：2，．求大长方形的面积．：3的长减去在D的长所得到的差之比为1的宽所得到的差，与的宽减去DD'比的应用；图形划分．考点：：：C=12，B：“在（1）中小长方形面积的比是：A：B=1要求大长方形的面积，需求出它的长和宽，由条件分析：的宽所得到的差，D．又知，长方形D'的宽减去，3B'：C'=1：3．而在（22）中相应的比例是A'：B'=1：′，D的宽是大长方形宽的”可知：D的宽是大长方形宽的，1与D'的长减去在D的长所得到的差之比为：3′﹣大长方形的宽），由此便可以列式计算．（×﹣大长方形的宽）D的长是×（28，D的长是28 ，则长为x28﹣x 解答：解：设大长方形的宽为′′D．=DD的宽=x，所以，的宽﹣的宽，=D因为的宽x′28×长D=（﹣）﹣=长，）xD（×28x，9 / 10 2长D：=由题设可知，于是=，即x=8．= 8于是，大长方形的长=28﹣8=20，从而大长方形的面积为×20=160平方厘米．答：大长方形的面积是160平方米．此题比较复杂，主要考查比的关系，应利用比的意义，找清数量见的比，再利用题目条件，就可以进行计点评：算求得结果．，左边部分面积是38，FG=6直线AB将图形分成两部分，CD=514．（2012?武汉模拟）如图，已知，DE=7，EF=15，．的面积是4065右边部分面积是，那么三角形ADG考点：三角形的周长和面积．分析：看成是一个整体，根据各线段的关系和左右两部分面积的关系，可以列出一个方程，求出可以把S ADE△S的关系求出答案．S的面积，然后再根据所求三角形与ADE△△ADE解答：=3S解：由题意知，S，S=，S BEC△ADEBFE△△AEG△X），（S=3X=X设S，则S，=38﹣BFEADE△△△AEG）（可列出方程：38﹣X+3X=65，，解方程，得：x=10 =40．）（=10×所以S1+3ADG△故答案为：40．此题考查了如何利用边的关系求三角形的面积．点评：10 / 10。

小学五年级各类题型奥数及答案面积计算(五年级奥数题)1、（05年三帆中学考题）右图中AB=3厘米，CD=12厘米，ED=8厘米，AF=7厘米.四边形ABDE的面积是( )平方厘米．2、如图，已知每个小正方形格的面积是1平方厘米，则不规则图形的面积是______．面积计算(答案)1、（05年三帆中学考题）右图中AB=3厘米，CD=12厘米，ED=8厘米，AF=7厘米.四边形ABDE的面积是( )平方厘米．解：阴影面积=1/2×ED×AF+1/2×AB×CD=1/2×8×7+1/2×3×12=28+18=46。

2、如图，已知每个小正方形格的面积是1平方厘米，则不规则图形的面积是______．解答：基本的格点面积的求解，可以用解答种这样的方法求解，当然也可以用格点面积公式来做，内部点有16个，周边点有8个，所以面积为16+8÷2-1=19图形面积(一)(五年级奥数题)1、（06年清华附中考题）如图，在三角形ABC中，D为BC的中点，E为AB上的一点，且BE=1 /3AB,已知四边形EDCA的面积是35，求三角形ABC的面积.2、正方形ABFD的面积为100平方厘米，直角三角形ABC的面积，比直角三角形（CDE的面积大30平方厘米，求DE的长是多少？ 04.jpg图形面积(一)(答案)1、（06年清华附中考题）如图，在三角形ABC中，D为BC的中点，E为AB上的一点，且BE=1 /3AB,已知四边形EDCA的面积是35，求三角形ABC的面积.解答：根据定理：所以四边形ACDE的面积就是6-1=5份，这样三角形35÷5×6=42。

2、正方形ABFD的面积为100平方厘米，直角三角形ABC的面积，比直角三角形（CDE的面积大30平方厘米，求DE的长是多少？解：公共部分的运用，三角形ABC面积-三角形CDE的面积=30，两部分都加上公共部分（四边形BCDF），正方形ABFD-三角形BFE=30，所以三角形BFE的面积为70，所以FE的长为70×2÷10=14，所以DE=4。

五年级奥数题：图形与面积一、填空题（共10 小题，每小题 3 分，满分30 分）1．（ 3 分）如图是由 16 个同样大小的正方形组成的，如果这个图形的面积是400 平方厘米，那么它的周长是_________厘米．2．（ 3 分）第一届保良局亚洲区城市小学数学邀请赛在7 月 21 日开幕，下面的图形中，每一小方格的面积是1．那么 7， 2， 1 三个数字所占的面积之和是_________．3．（ 3 分）如图中每一小方格的面积都是1 平方厘米，那么用粗线围成的图形面积是_________平方厘米．4．（ 3 分）（ 2014?长沙模拟）如图的两个正方形，边长分别为8 厘米和 4 厘米，那么阴影部分的面积是_________平方厘米．5．（ 3 分）在△ABC 中，BD=2DC ，AE=BE ，已知△ ABC 的面积是 18 平方厘米，则四边形 AEDC 的面积等于_________平方厘米．6．（ 3 分）如图是边长为 4 厘米的正方形，AE=5 厘米、 OB 是_________厘米．7．（ 3 分）如图正方形ABCD 的边长是 4 厘米， CG 是 3 厘米，长方形DEFG 的长 DG 是 5 厘米，那么它的宽DE 是_________ 厘米．8．（ 3 分）如图，一个矩形被分成10 个小矩形，其中有6 个小矩形的面积如图所示，那么这个大矩形的面积是_________．9．（3 分）如图，正方形ABCD 的边长为12， P 是边 AB 上的任意一点，M、 N、I、 H 分别是边 BC 、AD 上的三等分点， E、 F、 G 是边 CD 上的四等分点，图中阴影部分的面积是_________．10．（ 3 分）图中的长方形的长和宽分别是6 厘米和 4 厘米，阴影部分的总面积是10 平方厘米，四边形ABCD 的面积是_________平方厘米．二、解答题（共4 小题，满分0 分）11．图中正六边形ABCDEF 的面积是54． AP=2PF ， CQ=2BQ ，求阴影四边形CEPQ 的面积．12．如图，涂阴影部分的小正六角星形面积是16 平方厘米．问：大正六角星形面积是多少平方厘米．13．一个周长是56 厘米的大长方形，按图中（1）与（ 2）所示意那样，划分为四个小长方形．在（1）中小长方形面积的比是： A ：B=1 ：2， B： C=1： 2．而在（ 2）中相应的比例是A' ： B'=1 ： 3， B'： C'=1： 3．又知，长方形 D'的宽减去 D 的宽所得到的差，与D'的长减去在 D 的长所得到的差之比为1： 3．求大长方形的面积．14．（ 2012?武汉模拟）如图，已知 CD=5 ，DE=7 ，EF=15，FG=6 ，直线 AB 将图形分成两部分，左边部分面积是38，右边部分面积是 65，那么三角形 ADG 的面积是 _________ ．2010 年五年级奥数题：图形与面积（B）参考答案与试题解析一、填空题（共10 小题，每小题 3 分，满分30 分）1．（ 3 分）如图是由 16 个同样大小的正方形组成的，如果这个图形的面积是400 平方厘米，那么它的周长是170厘米．考点：巧算周长．分析：要求该图形的周长，先求出每个小正方形的面积，根据正方形的面积公式，得出小正方形的边长，然后先算出该图形的外周的长，因为内、外的长相等，再乘2 即可得出结论．解答：解：400÷16=25（平方厘米），因为 5×5=25（平方厘米），所以每个小正方形的边长为5 厘米，周长为：（ 5×4+5 ×4+5×3+5 ×2+5 ×3+5 ）×2，=85 ×2，=170 （厘米）；答：它的周长是170 厘米．点评：此类题解答的关键是先求出每个小正方形的面积，根据正方形的面积公式，得出小正方形的边长，进而算出该图形的外周的长，因为内、外的长相等，再乘2 即可得出结论．2．（ 3 分）第一届保良局亚洲区城市小学数学邀请赛在7 月 21 日开幕，下面的图形中，每一小方格的面积是1．那么 7， 2， 1 三个数字所占的面积之和是25．考点：组合图形的面积．分析：此题需要进行图形分解：“7”分成一个长方形、一个等腰直角三角形、一个平行四边形；“2”分成一个梯形、一个平行四边形、一个长方形；“1”分成一个梯形和两个长方形．然后进行图形转换，依据题目条件即可求出结果．解答：解：“7”所占的面积和 =+3+4=，“2”所占的面积和=3+4+3=10 ，“1”所占的面积和=+7=，那么 7， 2， 1 三个数字所占的面积之和= ++10=25 ．故答案为： 25．点评：此题关键是进行图形分解和转换．3．（ 3 分）如图中每一小方格的面积都是1 平方厘米，那么用粗线围成的图形面积是6.5平方厘米．考点：组合图形的面积．分析：由图可以观察出：大正方形的面积减粗线以外的图形面积即为粗线围成的图形面积．解答：解：大正方形的面积为4×4=16（平方厘米）；粗线以外的图形面积为：整格有 3 个，左上，右上，右中，右下，左中，右中，共有3++5× =9.5（平方厘米）；所以粗线围成的图形面积为16﹣ 9.5=6.5（平方厘米）；答：粗线围成的图形面积是6.5 平方厘米．故此题答案为：6.5．点评：此题关键是对图形进行合理地割补．4．（ 3 分）（2014?长沙模拟）如图的两个正方形，边长分别为8 厘米和 4 厘米，那么阴影部分的面积是24 平方厘米．考点：组合图形的面积．分析：两个正方形的面积减去两个空白三角形的面积．解答：解： 4×4+8×8﹣×4×（ 4+8）﹣×8×8，=16+64 ﹣ 24﹣ 32，=24 （ cm 2）；2答：阴影的面积是24cm ．点评：求组合图形面积的化为求常用图形面积的和与差求解．5．（3 分）在△ABC 中， BD=2DC ，AE=BE ，已知△ ABC 的面积是 18 平方厘米，则四边形 AEDC 的面积等于 12 平方厘米．考点：相似三角形的性质（份数、比例）；三角形的周长和面积．分析：根据题意，连接AD ，即可知道△ ABD 和△ ADC 的关系，△ADE 和△BDE 的关系，由此即可求出四边形AEDC 的面积．解答：解：连接AD ，因为 BD=2DC ，所以， S△ABD=2S △ ADC ，即， S△ABD=18 × =12 （平方厘米），又因为， AE=BE ，所以， S△ADE=S △ BDE ，即， S△ BDE=12 × =6（平方厘米），所以 AEDC 的面积是： 18﹣ 6=12 （平方厘米）；故答案为： 12．点评：解答此题的关键是，根据题意，添加辅助线，帮助我们找到三角形之间的关系，由此即可解答．6．（ 3 分）如图是边长为 4 厘米的正方形，AE=5 厘米、 OB 是 3.2厘米．考点：组合图形的面积．分析：连接BE、AF可以看出，三角形ABE 的面积是正方形面积的一半，再依据三角形面积公式就可以求出OB 的长度．解答：解：如图连接 BE、 AF ，则 BE 与 AF 相交于 D 点 S△ADE=S △ BDF则S△ ABE= S 正方形 =×（4×4）=8（平方厘米）；OB=8 ×2÷5=3.2（厘米）；答： OB 是 3.2 厘米．故答案为： 3.2．点评：此题主要考查三角形和正方形的面积公式，将数据代入公式即可．7．（ 3 分）如图正方形ABCD 的边长是 4 厘米， CG 是 3 厘米，长方形DEFG 的长 DG 是 5 厘米，那么它的宽DE 是 3.2 厘米．考点：组合图形的面积．分析：连接AG，则可以依据题目条件求出三角形AGD 的面积，因为DG 已知，进而可以求三角形AGD 的高，也就是长方形的宽，问题得解．解答：解：如图连接AGS △AGD =S 正方形ABCD ﹣ S △CDG ﹣ S △ABG ， =4 ×4﹣ 3×4÷2﹣ 1×4÷2 =16﹣6﹣2=8 （平方厘米）；8×2÷5=3.2（厘米）；答：长方形的宽是3.2 厘米． 故答案为： 3.2．点评：依据题目条件做出合适的辅助线，问题得解．8．（3 分）如图，一个矩形被分成10 个小矩形，其中有 6 个小矩形的面积如图所示，那么这个大矩形的面积是243．考点：组合图形的面积．分析：从图中可以看出每上、下两个小矩形的一个边是相邻的，也就是说长是相等的，那么根据矩形的面积公式知，如果长相同，面积之比也就是宽之比，反之宽之比也就是面积之比；由中间面积20 和 16 的矩形，可 以算出空着的小矩形面积，最后把所有小矩形面积加起来就是大矩形的面积．解答：解：由图和题意知，中间上、下小矩形的面积比是：20： 16=5： 4， 所以宽之比是5： 4，那么， A ： 36=5： 4 得 A=45 ； 25： B=5： 4 得 B=20 ； 30： C=5： 4 得 C=24 ； D ： 12=5： 4 得 D=15 ；所以大矩形的面积 =45+36+25+20+20+16+30+24+15+12=243 ；故答案为： 243．点评：此题考查了如果长方形的长相同，宽之比等于面积之比，还考查了比例的有关知识．9．（3 分）如图，正方形 ABCD 的边长为 12， P 是边 AB 上的任意一点， M 、 N 、I 、 H 分别是边 BC 、AD 上的三等分点， E 、 F 、 G 是边 CD 上的四等分点，图中阴影部分的面积是60 ．考点：组合图形的面积．分析：根据题意：正方形等分点， E 、F 、G 案．ABCD 的边长为 12，P 是边 AB是边 CD 上的四等分点，可连接上的任意一点， M 、 N 、 I 、 H 分别是边 BC 、 AD 上的三DP ，然后再利用三角形的面积公式进行计算即可得到答解答：解：阴影部分的面积=×DH×AP+×DG×AD+×EF×AD+×MN×BP=×4×AP+×3×12+×3×12+×4×BP=2AP+18+18+2BP=36+2 ×（AP+BP ）=36+2 ×12=36+24=60 ．答：这个图形阴影部分的面积是60．点评：此题主要考查的是三角形的面积公式．10．（ 3 分）图中的长方形的长和宽分别是 6 厘米和 4 厘米，阴影部分的总面积是 10 平方厘米，四边形 ABCD 的面积是 4 平方厘米．考点：重叠问题；三角形的周长和面积．分析：因为S△ EFC+S△ GHC=四边形EFGH面积÷2=12，S△ AEF+S△ AGH=四边形EFGH面积÷2=12，所以 S△ ABE+S △ ADH=S △ BFC+S △ DGC= 四边形 EFGH 面积÷2﹣阴影部分的总面积是 10 平方厘米 =2 平方厘米．所以：四边形ABCD 面积 =S△ ECH﹣（ S△ ABE+S △ ADH ） =四边形 ABCD 面积÷4﹣ 2=6﹣ 2=4 平方厘米．解答：解：由题意推出： S△ABE+S △ ADH=S △ BFC+S △DGC= 四边形 EFGH 面积÷2﹣阴影面积 10 平方厘米 =2 平方厘米．所以：四边形ABCD 面积 =S△ ECH﹣（ S△ ABE+S △ ADH ） =四边形 ABCD 面积÷4﹣ 2=6﹣ 2=4 平方厘米．故答案为： 4．点评：此题在重叠问题中考查了三角形的周长和面积公式，此题设计的非常精彩．二、解答题（共4 小题，满分0 分）11．图中正六边形ABCDEF 的面积是54． AP=2PF ， CQ=2BQ ，求阴影四边形CEPQ 的面积．考点：等积变形（位移、割补）．分析：如图，将正六边形ABCDEF 等分为 54 个小正三角形，根据平行四边形对角线平分平行四边形面积，采用数小三角形的办法来计算面积．解答：解：如图，S△ PEF=3 ， S△ CDE=9 ， S 四边形 ABQP=11 ．上述三块面积之和为3+9+11=23 ．因此，阴影四边形CEPQ 面积为 54﹣ 23=31 ．点评：此题主要利用面积分割，用数基本小三角形面积来解决问题．12．如图，涂阴影部分的小正六角星形面积是16 平方厘米．问：大正六角星形面积是多少平方厘米．考点：等积变形（位移、割补）．分析：由图及题意知，可把涂阴影部分小正六角星形等分成12 个小三角形，且都与外围的6 个空白小三角形面积相等，已知涂阴影部分的小正六角星形面积是16 平方厘米，可求出大正六角星形中心正六边形的面积，而这个正六边形又可等分成6 个小正三角形，且它们与外围六个大角的面积相等，进而可求出大正六角星形面积解答：解：如下图所示，涂阴影部分小正六角星形可等分成12 个小三角形，且都与外围的6 个空白小三角形面积相等，所以正六边形ABCDEF 的面积： 16÷12×（ 12+6）=24 （平方厘米）；又由于正六边形ABCDEF 又可等分成6 个小正三角形，且它们与外围六个大角的面积相等，所以大正六角星形面积：24×2=48（平方厘米）；答：大正六角星形面积是48 平方厘米．点评：此题要借助求正六边形的面积来解答，它既可看作是18 个小正三角形，又可看作是6 个大点的正三角形组成．13．一个周长是56 厘米的大长方形，按图中（1）与（ 2）所示意那样，划分为四个小长方形．在（1）中小长方形面积的比是： A ：B=1 ：2， B： C=1： 2．而在（ 2）中相应的比例是A' ： B'=1 ： 3， B'： C'=1： 3．又知，长方形 D'的宽减去 D 的宽所得到的差，与D'的长减去在 D 的长所得到的差之比为1： 3．求大长方形的面积．考点：比的应用；图形划分．分析：要求大长方形的面积，需求出它的长和宽，由条件“在（ 1）中小长方形面积的比是： A ：B=1 ：2，B：C=1 ：2．而在（ 2）中相应的比例是A' ： B'=1 ： 3， B'： C'=1： 3．又知，长方形 D'的宽减去 D 的宽所得到的差，与 D'的长减去在 D 的长所得到的差之比为1：3”可知： D 的宽是大长方形宽的′，，D 的宽是大长方形宽的′×（ 28﹣大长方形的宽），由此便可以列式计算．D 的长是×（ 28﹣大长方形的宽）， D 的长是解答：解：设大长方形的宽为x，则长为 28﹣x′′因为 D 的宽 = x， D的宽 =x，所以， D的宽﹣ D 的宽= ．′×（ 28﹣x），D 长 = ×（28﹣ x），D 长 =′D长﹣D长=×（ 28﹣ x），由题设可知：=即= ，于是= ， x=8 ．于是，大长方形的长=28 ﹣ 8=20，从而大长方形的面积为8×20=160 平方厘米．答：大长方形的面积是160 平方米．点评：此题比较复杂，主要考查比的关系，应利用比的意义，找清数量见的比，再利用题目条件，就可以进行计算求得结果．14．（ 2012?武汉模拟）如图，已知 CD=5 ，DE=7 ，EF=15，FG=6 ，直线 AB 将图形分成两部分，左边部分面积是38，右边部分面积是 65，那么三角形 ADG 的面积是 40 ．考点：三角形的周长和面积．分析：可以把S△ADE看成是一个整体，根据各线段的关系和左右两部分面积的关系，可以列出一个方程，求出S△ADE的面积，然后再根据所求三角形与S△ADE的关系求出答案．解答：解：由题意知， S△AEG=3S△ADE， S△BFE=S△BEC，设 S△ADE =X ，则 S△AEG =3X ， S△BFE=（38﹣X），可列出方程：（ 38﹣ X） +3X=65 ，解方程，得：x=10 ，所以 S△ADG=10×（ 1+3 ）=40 ．故答案为： 40．点评：此题考查了如何利用边的关系求三角形的面积．。

巧求表面积教课目的掌握长方体和正方体的特色、表面积和体积计算公式，并能运用公式解决一些实质问题。

教课过程一、例题解说我们已经学习了长方体和正方体，知道长方体或正方体六个面面积的总和叫做长方体或正方体的表面积。

假如长方体的长用 a 表示、宽用 b 表示、高用 h 表示，那么，长方体的表面积 =（ ab＋ ah＋ bh ）× 2。

假如正方体的棱长用 a 表示，则正方体的表面积=6a2。

关于由几个长方体或正方体组合而成的几何体，或许是一个长方体或正方体组合而成的几何形体，它们的表面积又怎样求呢？波及立体图形的问题，常常可考察同学们的看图能力和空间想象能力。

小学阶段碰到的立体图形主假如长方体和正方体，这些图形的特色都是能够从六个方向去看，特别是求表面积时，就是上下、左右和前后六个方向（有时只考虑上、左、前三个方向）的平面图形的面积的总和。

有了这个原则，在解决近似问题时就十分方便了。

例 1在一个棱长为 5 分米的正方体上放一个棱长为 4 分米的小正方体（下列图），求这个立体图形的表面积。

（例 1 图）（例2图）剖析我们把上边的小正方体想象成是能够向下“压缩” 的，“压缩” 后我们发现：小正方体的上边与大正方体上边中的暗影部分合在一同，正好是大正方体的上边。

这样这个立体图形有表面积就能够分红这样两部分：上下方向：大正方体的两个底面；侧面：小正方体的四个侧面大正方体的四个侧面。

解：上下方向：5× 5× 2=50（平方分米）侧面：5× 5×4=100（平方分米）4× 4× 4=64（平方分米）这个立体图形的表面积为：50＋ 100＋64=214（平方分米）答：这个立体图形的表面积为214 平方分米。

例 2下列图是一个棱长为 2 厘米的正方体，在正方体上表面的正中，向下挖一个棱长为 1 厘米的正方体小洞，接着在小洞的底面正中向下挖一个棱长为1厘米的正方体2小洞，第三个正方体小洞的挖法与前两个同样，棱长为1厘米。