2008徐州中考数学试卷3页

江苏省徐州市2008年中考数学试题及答案解析(word版) 本试卷分第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷1至2页，第Ⅱ卷3至8页.全卷共120分，考试时间120分钟.第Ⅰ卷注意事项：1.答Ⅰ第卷前考生务必将自己的考试证号、考试科目用2B铅笔填涂在答题卡上.2.作答选择题必须用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动，请用橡皮擦干净后，再选涂其它答案.不能答在第Ⅰ卷上.一、选择题（每小题2分，共20分.在每小题给出的四个选项中，有且只有．．．．一个是正确的）1.4的平方根是A.2± B.2 C. －2 D 162.一方有难、八方支援，截至5月26日12时，徐州巿累计为汶川地震灾区捐款约为11 180万元，该笔善款可用科学记数法表示为A. 11.18×103万元B. 1.118×104万元C. 1.118×105万元D. 1.118×108万元3.函数11yx=+中自变量x的取值范围是A. x≥－1B. x≤－1C. x≠－1D. x＝－14.下列运算中，正确的是A.x3+x3=x6B. x3·x9=x27C.(x2)3=x5D. x÷x2=x－15.如果点（3，－4）在反比例函数kyx=的图象上，那么下列各点中，在此图象上的是A.（3,4）B. （－2，－6）C.（－2，6）D.（－3，－4）6.下列平面展开图是由5个大小相同的正方形组成，其中沿正方形的边不能．．折成无盖．．小方盒的是A B C D7.⊙O1和⊙O2的半径分别为5和2，O1O2＝3，则⊙O1和⊙O2的位置关系是A.内含B. 内切C.相交D.外切8.下列图形中，是轴对称图形但不是中心对称图形的是A.正三角形B.菱形C.直角梯形D.正六边形9.下列事件中，必然事件是A.抛掷1个均匀的骰子，出现6点向上B.两直线被第三条直线所截，同位角C.366人中至少有2人的生日相同D.实数的绝对值是非负数 10.如图，小明随意向水平放置的大正方形内部区域抛一个小球，则小球停在小正方形内部（阴影）区域的概率为A. 34B. 13C. 12D. 14二、填空题（每小题3分，共18分.请将答案填写在第Ⅱ卷相应的位置上．．．．．．．．．．．．．．．．） 11.因式分解：2x 2-8=______▲________12.徐州巿部分医保定点医院2008年第一季度的人均住院费用（单位：元）约为：12 320，11 880,10 370,8 570,10 640, 10240.这组数据的极差是_____▲_______元.13.若12,x x 为方程210x x +-=的两个实数根，则12x x +=___▲___. 14.边长为a 的正三角形的面积等于______▲______.15.如图,AB 是⊙O 的直径，点C 在AB 的延长线上，CD 与⊙O 相切于点D.若，若∠C ＝18°，则∠CDA ＝______▲_______.16.如图，Rt △ABC 中，∠B ＝90°，AB ＝3cm ，AC ＝5cm ，将△ABC 折叠，使点C 与A 重合，得折痕DE ，则△ABE 的周长等于____▲_____cm.第Ⅱ卷三、解答题（每小题5分，共20分） 17.计算：2008011(1)()3π--+-18.已知21,23.x x x =+--求的值19.解不等式组12215(1)xx x ⎧>-⎪⎨⎪+≥-⎩，并写出它的所有整数解.（第10题图）（第15题图）（第16题图）20.如图，一座堤坝的横截面是梯形，根据图中给出的数据，求坝高和坝底宽（精确到0.1m ）1.4141.732四、解答题（本题有A 、B 两类题，A 类题4分，B类题6分，你可以根据自己的学习情况，在两类题中任意选做一题．．．．．．，如果两类题都做，则以A 类题计分） 21.（A 类）已知如图，四边形ABCD 中，AB ＝BC ，AD ＝CD ，求证：∠A ＝∠C. （B 类）已知如图，四边形ABCD 中，AB ＝BC ，∠A ＝∠C ，求证：AD ＝CD.五、解答题（每小题7分，共21分）22.从称许到南京可乘列车A 与列车B ，已知徐州至南京里程约为350km ，A 与B 车的平均速度之比为10∶7，A 车的行驶时间比B 车的少1h ，那么两车的平均速度分别为多少？23.小王某月手机话费中的各项费用统计情况见下列图表，请你根据图表信息完成下列各题：（1） 该月小王手机话费共有多少元？（2） 扇形统计图中，表示短信费的扇形的圆心角为多少度？ （3） 请将表格补充完整； （4） 请将条形统计图补充完整.24.如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC 的顶点短信费长途话费基本话费月功能费5040302010项目金额/元DCBAB（第20题图）（第21题图）均在格点上，点B 的坐标为（1,0） ①画出△ABC 关于x 轴对称的△A 1B 1C 1，②画出将△ABC 绕原点O 按逆时针旋转90°所得的△A 2B 2C 2，③△A 1B 1C 1与△A 2B 2C 2成轴对称图形吗？若成轴对称图形，画出所有的对称轴；④△A 1B 1C 1与△A 2B 2C 2成中心对称图形吗？若成中心对称图形，写出所有的对称中心的坐标.六、解答题（每小题8分，共16分）25.为缓解油价上涨给出租车待业带来的成本压力，某巿自2007年11月17日起，调整出租车运价，调整方案见下列表格及图像（其中a,b,c 为常数）设行驶路程xkm 时，调价前的运价y 1（元），调价后的运价为y 2（元）如图，折线ABCD 表示y 2与x 之间的函数关系式，线段EF 表示当0≤x ≤3时，y 1与x 的函数关系式，根据图表信息，完成下列各题： ①填空：a=______,b=______,c=_______.②写出当x ＞3时，y 1与x 的关系，并在上图中画出该函数的图象.③函数y1与y 2的图象是否存在交点？若存在，求出交点的坐标，并说明该点的实际意义，若不存在请说明理由.26.已知四边形ABCD 的对角线AC 与BD 交于点O,给出下列四个论断 ① OA ＝OC ② AB ＝CD ③ ∠BAD ＝∠DCB ④ AD ∥BC请你从中选择两个论断作为条件,以“四边形ABCD 为平行四边形”作为结论,完成下列各题：①构造一个真命题．．．，画图并给出证明； ②构造一个假命题．．．，举反例加以说明.七、解答题（第27题8分，第28题10分，共18分）27.已知二次函数的图象以A （－1，4）为顶点，且过点B （2，－5） ①求该函数的关系式；②求该函数图象与坐标轴的交点坐标；③将该函数图象向右平移，当图象经过原点时，A 、B 两点随图象移至A ′、B ′， 求△O A ′B ′的面积.28.如图1，一副直角三角板满足AB ＝BC ，AC ＝DE ，∠ABC ＝∠DEF ＝90°，∠EDF ＝30°【操作】将三角板DEF 的直角顶点E 放置于三角板ABC 的斜边AC 上，再将三角板．．．．DEF ．．．绕点．．E ．旋转．．，并使边DE 与边AB 交于点P ，边EF 与边BC 于点Q 【探究一】在旋转过程中， （1） 如图2，当CE1EA＝时，EP 与EQ 满足怎样的数量关系？并给出证明. （2） 如图3，当CE2EA＝时EP 与EQ 满足怎样的数量关系？，并说明理由. （3） 根据你对（1）、（2）的探究结果，试写出当CEEA＝m 时，EP 与EQ 满足的数量关系式 为_________,其中m 的取值范围是_______(直接写出结论，不必证明)【探究二】若，AC ＝30cm ，连续PQ ，设△EPQ 的面积为S(cm 2)，在旋转过程中：（1） S 是否存在最大值或最小值？若存在，求出最大值或最小值，若不存在，说明理由. （2） 随着S 取不同的值，对应△EPQ 的个数有哪些变化？不出相应S 值的取值范围.徐州巿2008年初中毕业、升学考试数 学 试 题 参 考 答 案1.A2.B3.C4.D5.C6.B7.B8.C9.D 10.C 11. 2(2)(2)x x -+ 12. 3750元 13.－114.215.126° FC(E)A(D)Q PDEFCBAQPDEFCBA16.7cm17.解：原式＝1＋1－3＋2＝118.解：223(3)(1)x x x x --=-+，将1x =代入到上式，则可得223111)2)1x x --=-+==-19.解：12215(1)xx x ⎧>-⎪⎨⎪+≥-⎩222221552x x x x x x >->-⎧⎧⇒⇒-<≤⎨⎨+≥-≤⎩⎩20.解：如图所示，过点A 、D 分别作BC 的垂线AE 、DF 分别交BC 于点E 、F ， 所以△ABE 、△CDF 均为Rt △，又因为CD ＝14，∠DCF ＝30°，所以DF ＝7＝AE ，且FC ＝12.1所以BC ＝7＋6＋12.1＝25.1m. 21.证明：（A ） 连结AC ，因为AB ＝AC ， 所以∠BAC ＝∠BCA ，同理AD ＝CD 得∠DAC ＝∠DCA所以∠A ＝∠BAC ＋∠DAC ＝∠BCA ＋∠DCA ＝∠C （B ）如（A ）只须反过来即可.22.解方程的思想.A 车150km/h ，B 车125km/h.23.解：（1）125元的总话费 （2）72° （3）（4）CBE FDCBA5040302010金额/元24. 解：如下图所示，（4）对称中心是（0，0）25.解：(1) a=7, b=1.4, c=2.1 （2）1 2.10.3y x =- （3）有交点为31(,9)7其意义为当317x <时是方案调价前合算，当317x >时方案调价后合算. 26.解：（1）②③为论断时，（2）②④为论断时，此时可以构成一梯形. 27.解：（1）223y x x =--+ （2） （0,3），（－3,0），（1,0） （3）略。

徐州巿2022年中考往年真题练习: 初中毕业、升学考试数学试题本试卷分第Ⅰ卷和第Ⅱ卷两部分, 第Ⅰ卷1至2页, 第Ⅱ卷3至8页. 全卷共120分, 考试时间120分钟.第Ⅰ卷注意事项:1. 答Ⅰ第卷前考生务必将自己的考试证号、考试科目用2B铅笔填涂在答题卡上.2. 作答挑选题必须用2B铅笔把答题卡上对应题目的答案标号涂黑. 如需改动, 请用橡皮擦干净后, 再选涂其它答案. 不能答在第Ⅰ卷上.一、挑选题（每小题2分, 共20分. 在每小题给出的四个选项中, 有且只有．．．．一个是正确的 )1. 4的平方根是A. 2± B. 2 C. －2 D 162. 一方有难、八方支援, 截至5月26日12时, 徐州巿累计为汶川地震灾区捐款约为11 180万元, 该笔善款可用科学记数法表示为A. 11. 18×103万元B. 1. 118×104万元C. 1. 118×105万元D. 1. 118×108万元3. 函数11yx=+中自变量x的取值范围是A. x≥－1B. x≤－1C. x≠－1D. x＝－14. 下列运算中, 正确的是A. x3+x3=x6B. x3·x9=x27C. (x2) 3=x5D. x÷x2=x－15. 加入点（3, －4) 在反比例函数kyx=的图象上, 那么下列各点中, 在此图象上的是A. （3, 4)B. （－2, －6)C. （－2, 6)D. （－3, －4)6. 下列平面展开图是由5个大小一样的正方形组成, 其中沿正方形的边不能．．折成无．盖．小方盒的是A B C D7. ⊙O 1和⊙O 2的 半径分别为5和2, O 1O 2＝3, 则⊙O 1和⊙O 2的 位置关系是A. 内含B. 内切C. 相交D. 外切 8. 下列图形中, 是 轴对称图形但不是 中心对称图形的 是A. 正三角形B. 菱形C. 直角梯形D. 正六边形 9. 下列事件中, 必定事件是A. 抛掷1个均匀的 骰子, 出现6点向上B. 两直线被第三条直线所截, 同位角C. 366人中至少有2人的 生日一样D. 实数的 绝对值是 非负数10. 如图, 小明随意向水平放置的 大正方形内部区域抛一个小球, 则小球停在小正方形内部（阴影) 区域的 概率为A.34 B. 13 C. 12 D. 14二、 填空题（每小题3分, 共18分. 请将答案填写在第Ⅱ卷相应．．．．．．．．．．．．的． 位置上．．．) 11. 因式分解: 2x 2-8=______▲________12. 徐州巿部分医保定点医院2022年中考往年真题练习: 第一季度的 人均住院费用（单位: 元) 约为: 12 320, 11 880, 10 370, 8 570, 10 640, 10240. 这组数据的 极差是 _____▲_______元.13. 若12,x x 为方程210x x +-=的 两个实数根, 则12x x +=___▲___. 14. 边长为a 的 正三角形的 面积等于______▲______.15. 如图, AB 是 ⊙O 的 直径, 点C 在AB 的 延长线上, CD 与⊙O 相切于点D. 若, 若∠C ＝18°, 则∠CDA ＝______▲_______.（第10题图)（第15题图)（第16题图)16. 如图, Rt △ABC 中, ∠B ＝90°, AB ＝3cm, AC ＝5cm, 将△ABC 折叠, 使点C 与A 重合, 得折痕DE, 则△ABE 的 周长等于____▲_____cm.第Ⅱ卷三、 解答题（每小题5分, 共20分)17. 计算: 2008011(1)()3π--+-+18.已知21,23.x x x =+--求的值19. 解不等式组12215(1)xx x ⎧>-⎪⎨⎪+≥-⎩, 并写出它的 所有整数解.20. 如图, 一座堤坝的 横截面是 梯形, 根据图中给出的 数据, 求坝高和坝底宽（精确到0. 1m) 参考数据1. 732四、 解答题（本题有A 、 B 两类题, A 类题4分, B 类题6分, 你可以根据自己的 学习情况, 在两类题中任意选做一题．．．．．．, 加入两类题都做, 则以A 类题计分) 21. （A 类) 已知如图, 四边形ABCD 中, AB ＝BC, AD ＝CD, 求证: ∠A ＝∠C.（B 类) 已知如图, 四边形ABCD 中, AB ＝BC, ∠A ＝∠C, 求证: AD ＝CD.ACB（第20题图)五、 解答题（每小题7分, 共21分)22. 从称许到南京可乘列车A 与列车B, 已知徐州至南京里程约为350km, A 与B 车的 平均速度之比为10∶7, A 车的 行驶时间比B 车的 少1h, 那么两车的 平均速度分别为几 ？23. 小王某月手机话费中的 各项费用统计情况见下列图表, 请你根据图表信息完成下列各题:（1） 该月小王手机话费共有几 元？（2） 扇形统计图中, 表示短信费的 扇形的 圆心角为几度？ （3） 请将表格补充完整； （4） 请将条形统计图补充完整.50403020100项目金额/元（第21题图)24. 如图, 方格纸中的 每个小方格都是 边长为1个单位的 正方形, 在建立平面直角坐标系后, △ABC 的 顶点均在格点上, 点B 的 坐标为（1, 0) ①画出△ABC 关于x 轴对称的 △A 1B 1C 1,②画出将△ABC 绕原点O 按逆时针旋转90°所得的 △A 2B 2C 2,③△A 1B 1C 1与△A 2B 2C 2成轴对称图形吗？若成轴对称图形, 画出所有的 对称轴； ④△A 1B 1C 1与△A 2B 2C 2成中心对称图形吗？若成中心对称图形, 写出所有的 对称中心的 坐标.六、 解答题（每小题8分, 共16分)25. 为缓解油价上涨给出租车待业带来的 成本压力, 某巿自2021年11月17日起, 调整出租车运价,调整方案见下列表格及图像（其中a, b, c 为常数)设行驶路程xkm 时, 调价前的 运价y 1（元) , 调价后的 运价为y 2（元) 如图, 折线ABCD 表示y 2与x 之间的 函数关系式, 线段EF 表示当0≤x ≤3时, y 1与x 的 函数关系式, 根据图表信息, 完成下列各题: ①填空: a=______, b=______, c=_______.②写出当x ＞3时, y 1与x 的 关系, 并在上图中画出该函数的 图象.③函数y 1与y 2的 图象是 否存在交点？若存在, 求出交点的 坐标, 并说明该点的 实际意义, 若不存在请说明理由.26. 已知四边形ABCD 的 对角线AC 与BD 交于点O, 给出下列四个论断① OA ＝OC ② AB ＝CD ③ ∠BAD ＝∠DCB ④ AD ∥BC请你从中挑选两个论断作为条件, 以“四边形ABCD 为平行四边形”作为结论, 完成下列各题:①构造一个真命题．．．, 画图并给出证明； ②构造一个假命题．．．, 举反例加以说明.七、 解答题（第27题8分, 第28题10分, 共18分)27. 已知二次函数的 图象以A （－1, 4) 为顶点, 且过点B （2, －5)①求该函数的 关系式；②求该函数图象与坐标轴的 交点坐标；③将该函数图象向右平移, 当图象经过原点时, A 、 B 两点随图象移至A ′、 B ′, 求△O A ′B ′的 面积.28. 如图1, 一副直角三角板满足AB ＝BC, AC ＝DE, ∠ABC ＝∠DEF ＝90°, ∠EDF ＝30°【操作】将三角板DEF 的 直角顶点E 放置于三角板ABC 的 斜边AC 上, 再将三角板．．．．DEF ．．．绕点．．E ．旋转．．, 并使边DE 与边AB 交于点P, 边EF 与边BC 于点Q 【探究一】在旋转过程中, （1） 如图2, 当CE1EA＝时, EP 与EQ 满足怎样的 数量关系？并给出证明. （2） 如图3, 当CE2EA＝时EP 与EQ 满足怎样的 数量关系？, 并说明理由. （3） 根据你对（1) 、 （2) 的 探究结果, 试写出当CEEA＝m 时, EP 与EQ 满足的 数量关系式为_________, 其中m 的 取值范围是 _______(直接写出结论, 不必证明)【探究二】若, AC ＝30cm, 连续PQ, 设△EPQ 的 面积为S(cm 2) , 在旋转过程中: （1） S 是 否存在最大值或最小值？若存在, 求出最大值或最小值, 若不存在, 说明理由.（2） 随着S 取不同的 值, 对应△EPQ 的 个数有哪些变化？不出相应S 值的 取值范围.F C(E)B A(D)Q PDEFCBAQPDEFCBA（图1) （图2) （图3)徐州巿2022年中考往年真题练习: 初中毕业、 升学考试 数 学 试 题 参 考 答 案1. A2. B3. C4. D5. C6. B7. B8. C9. D 10. C 11. 2(2)(2)x x -+ 12. 3750元 13. －114. 215. 126° 16. 7cm17. 解: 原式＝1＋1－3＋2＝118. 解: 223(3)(1)x x x x --=-+,将1x =代入到上式, 则可得223111)2)1x x --=-+==-19. 解: 12215(xx x ⎧>-⎪⎨⎪+≥-⎩ 222221552x x x x x x >->-⎧⎧⇒⇒-<≤⎨⎨+≥-≤⎩⎩20. 解: 如图所示, 过点A 、 D 分别作BC 的 垂线AE 、 DF 分别交BC 于点E 、 F, 所以△ABE 、 △CDF 均为Rt △, 又因为CD ＝14, ∠DCF ＝30°, 所以DF ＝7＝AE, 且FC ＝12. 1所以BC ＝7＋6＋12. 1＝25. 1m. 21. 证明: （A) 连结AC, 因为AB ＝AC, 所以∠BAC ＝∠BCA, 同理AD ＝CD 得∠DAC ＝∠DCA所以∠A ＝∠BAC ＋∠DAC ＝∠BCA ＋∠DCA ＝∠C （B) 如（A) 只须反过来即可.22. 解方程的 思想. A 车150km/h, B 车125km/h.23. 解: （1) 125元的 总话费 （2) 72° （3)CBE FDCBA（4)24. 解: 如下图所示, （4)对称中心是 （0, 0)25. 解: (1) a=7, b=1. 4, c=2. 1 （2) 1 2.10.3y x=-50403020100项目金额/元（3) 有交点为31(,9)7其意义为当317x<时是方案调价前合算, 当317x>时方案调价后合算.26. 解: （1) ②③为论断时,（2) ②④为论断时, 此时可以构成一梯形. 27. 解: （1) 223y x x=--+（2) （0, 3) , （－3, 0) , （1, 0) （3) 略。

徐州巿2008年初中毕业、升学考试数学试题本试卷分第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷1至2页，第Ⅱ卷3至8页.全卷共120分，考试时间120分钟.第Ⅰ卷注意事项：1.答Ⅰ第卷前考生务必将自己的考试证号、考试科目用2B铅笔填涂在答题卡上.2.作答选择题必须用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动，请用橡皮擦干净后，再选涂其它答案.不能答在第Ⅰ卷上.一、选择题（每小题2分，共20分.在每小题给出的四个选项中，有且只有．．．．一个是正确的）1.4的平方根是A.2±B.2C.－2 D 162.一方有难、八方支援，截至5月26日12时，徐州巿累计为汶川地震灾区捐款约为11 180万元，该笔善款可用科学记数法表示为A.11.18×103万元B. 1.118×104万元C. 1.118×105万元D. 1.118×108万元3.函数11yx=+中自变量x的取值范围是A. x≥－1B. x≤－1C.x≠－1D.x＝－14.下列运算中，正确的是A.x3+x3=x6B. x3·x9=x27C.(x2)3=x5D. x÷x2=x－15.如果点（3，－4）在反比例函数kyx=的图象上，那么下列各点中，在此图象上的是A.（3,4）B.（－2，－6）C.（－2，6）D.（－3，－4）6.下列平面展开图是由5个大小相同的正方形组成，其中沿正方形的边不能．．折成无盖．．小方盒的是A BC D7.⊙O 1和⊙O 2的半径分别为5和2，O 1O 2＝3，则⊙O 1和⊙O 2的位置关系是A.内含B. 内切C.相交D.外切 8.下列图形中，是轴对称图形但不是中心对称图形的是A.正三角形B.菱形C.直角梯形D.正六边形 9.下列事件中，必然事件是A.抛掷1个均匀的骰子，出现6点向上B.两直线被第三条直线所截，同位角C.366人中至少有2人的生日相同D.实数的绝对值是非负数10.如图，小明随意向水平放置的大正方形内部区域抛一个小球，则小球停在小正方形内部（阴影）区域的概率为A.34 B. 13 C. 12 D. 14二、填空题（每小题3分，共18分.请将答案填写在第Ⅱ卷相应的位置上．．．．．．．．．．．．．．．．） 11.因式分解：2x 2-8=______▲________12.徐州巿部分医保定点医院2008年第一季度的人均住院费用（单位：元）约为：12 320，11 880,10 370,8 570,10 640, 10240.这组数据的极差是_____▲_______元. 13.若12,x x 为方程210x x +-=的两个实数根，则12x x +=___▲___. 14.边长为a 的正三角形的面积等于______▲______.15.如图,AB 是⊙O 的直径，点C 在AB 的延长线上，CD 与⊙O 相切于点D.若，若∠C ＝18°，则∠CDA ＝______▲_______.16.如图，Rt △ABC 中，∠B ＝90°，AB ＝3cm ，AC ＝5cm ，将△ABC 折叠，使点C 与A 重合，得折痕DE ，则△ABE 的周长等于____▲_____cm.第Ⅱ卷（第10题图）（第15题图）（第16题图）三、解答题（每小题5分，共20分）17.计算：2008011(1)()3π--+-+18.已知21,23.x x x =--求的值19.解不等式组12215(1)xx x ⎧>-⎪⎨⎪+≥-⎩，并写出它的所有整数解.20.如图，一座堤坝的横截面是梯形，根据图中给出的数据，求坝高和坝底宽（精确到0.1m ） 2 1.4143 1.732四、解答题（本题有A 、B 两类题，A 类题4分，B 类题6分，你可以根据自己的学习情况，在两类题中任意选做一题．．．．．．，如果两类题都做，则以A 类题计分） 21.（A 类）已知如图，四边形ABCD 中，AB ＝BC ，AD ＝CD ，求证：∠A ＝∠C.（B 类）已知如图，四边形ABCD 中，AB ＝BC ，∠A ＝∠C ，求证：AD ＝CD.五、解答题（每小题7分，共21分）22.从称许到南京可乘列车A 与列车B ，已知徐州至南京里程约为350km ，A 与B 车的平均速度之比为10∶7，A 车的行驶时间比B 车的少1h ，那么两车的平均速度分别为多少？ 23.小王某月手机话费中的各项费用统计情况见下列图表，请你根据图表信息完成下列各DCBAB（第20题图）（第21题图）题：（1） 该月小王手机话费共有多少元？（2） 扇形统计图中，表示短信费的扇形的圆心角为多少度？ （3） 请将表格补充完整； （4） 请将条形统计图补充完整.24.如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC 的顶点均在格点上，点B 的坐标为（1,0） ①画出△ABC 关于x 轴对称的△A 1B 1C 1，②画出将△ABC 绕原点O 按逆时针旋转90°所得的△A 2B 2C 2，③△A 1B 1C 1与△A 2B 2C 2成轴对称图形吗？若成轴对称图形，画出所有的对称轴；短信费长途话费基本话费月功能费50403020100项目金额/元④△A 1B 1C 1与△A 2B 2C 2成中心对称图形吗？若成中心对称图形，写出所有的对称中心的坐标.六、解答题（每小题8分，共16分）25.为缓解油价上涨给出租车待业带来的成本压力，某巿自2007年11月17日起，调整出租车运价，调整方案见下列表格及图像（其中a,b,c 为常数）设行驶路程xkm 时，调价前的运价y 1（元），调价后的运价为y 2（元）如图，折线ABCD 表示y 2与x 之间的函数关系式，线段EF 表示当0≤x ≤3时，y 1与x 的函数关系式，根据图表信息，完成下列各题： ①填空：a=______,b=______,c=_______.②写出当x ＞3时，y 1与x 的关系，并在上图中画出该函数的图象.③函数y 1与y 2的图象是否存在交点？若存在，求出交点的坐标，并说明该点的实际意义，若不存在请说明理由.26.已知四边形ABCD的对角线AC与BD交于点O,给出下列四个论断①OA＝OC②AB＝CD③∠BAD＝∠DCB④AD∥BC请你从中选择两个论断作为条件,以“四边形ABCD为平行四边形”作为结论,完成下列各题：①构造一个真命题．．．，画图并给出证明；②构造一个假命题．．．，举反例加以说明.七、解答题（第27题8分，第28题10分，共18分）27.已知二次函数的图象以A（－1，4）为顶点，且过点B（2，－5）①求该函数的关系式；②求该函数图象与坐标轴的交点坐标；③将该函数图象向右平移，当图象经过原点时，A、B两点随图象移至A′、B′，求△O A′B′的面积.28.如图1，一副直角三角板满足AB＝BC，AC＝DE，∠ABC＝∠DEF＝90°，∠EDF＝30°【操作】将三角板DEF的直角顶点E放置于三角板ABC的斜边AC上，再将三角板．．．．DEF．．．绕点．．E．旋转．．，并使边DE与边AB交于点P，边EF与边BC于点Q【探究一】在旋转过程中，（1）如图2，当CE1EA＝时，EP与EQ满足怎样的数量关系？并给出证明.（2） 如图3，当CE2EA＝时EP 与EQ 满足怎样的数量关系？，并说明理由. （3） 根据你对（1）、（2）的探究结果，试写出当CEEA＝m 时，EP 与EQ 满足的数量关系式为_________,其中m 的取值范围是_______(直接写出结论，不必证明)【探究二】若，AC ＝30cm ，连续PQ ，设△EPQ 的面积为S(cm 2)，在旋转过程中： （1） S 是否存在最大值或最小值？若存在，求出最大值或最小值，若不存在，说明理由.（2） 随着S 取不同的值，对应△EPQ 的个数有哪些变化？不出相应S 值的取值范围.F C(E)B A(D)Q PDEFCBAQPDEFCBA（图1） （图2） （图3）徐州巿2008年初中毕业、升学考试数 学 试 题 参 考 答 案1.A2.B3.C4.D5.C6.B7.B8.C9.D 10.C 11. 2(2)(2)x x -+ 12. 3750元 13.－1 14.215.126° 16.7cm17.解：原式＝1＋1－3＋2＝118.解：223(3)(1)x x x x --=-+，将1x =+代入到上式，则可得223111)2)1x x --=-+==-19.解：12215(1)xx x ⎧>-⎪⎨⎪+≥-⎩222221552x x x x x x >->-⎧⎧⇒⇒-<≤⎨⎨+≥-≤⎩⎩20.解：如图所示，过点A 、D 分别作BC 的垂线AE 、DF 分别交BC 于点E 、F ， 所以△ABE 、△CDF 均为Rt △，又因为CD ＝14，∠DCF ＝30°，所以DF ＝7＝AE ，且FC ＝312.1所以BC ＝7＋6＋12.1＝25.1m. 21.证明：（A ）连结AC ，因为AB ＝AC ，所以∠BAC ＝∠BCA ，同理AD ＝CD 得∠DAC ＝∠DCA所以∠A ＝∠BAC ＋∠DAC ＝∠BCA ＋∠DCA ＝∠C（B ）如（A ）只须反过来即可.22.解方程的思想.A 车150km/h ，B 车125km/h. 23.解：（1）125元的总话费 （2）72° （3）BE FDCBA（4） 解：如下图所示，24.（4）对称中心是（0，0） 25.解：(1) a=7, b=1.4, c=2.1 （2）1 2.10.3y x =- （3）有交点为31(,9)7其意义为当317x <时是方案调价前合算，当317x >时方案调价后合算. 26.解：（1）②③为论断时，（2）②④为论断时，此时可以构成一梯形. 27.解：（1）223y x x =--+ （2） （0,3），（－3,0），（1,0） （3）略短信费长途话费基本话费月功能费50403020100项目金额/元。

徐州巿2008年初中毕业、升学考试数学试题本试卷分第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷1至2页，第Ⅱ卷3至8页.全卷共120分，考试时间120分钟.第Ⅰ卷注意事项：1.答Ⅰ第卷前考生务必将自己的考试证号、考试科目用2B铅笔填涂在答题卡上.2.作答选择题必须用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动，请用橡皮擦干净后，再选涂其它答案.不能答在第Ⅰ卷上.一、选择题（每小题2分，共20分.在每小题给出的四个选项中，有且只有．．．．一个是正确的）1.4的平方根是A.2± B.2 C. －2 D 162.一方有难、八方支援，截至5月26日12时，徐州巿累计为汶川地震灾区捐款约为11 180万元，该笔善款可用科学记数法表示为A. 11.18×103万元B. 1.118×104万元C. 1.118×105万元D. 1.118×108万元3.函数11yx=+中自变量x的取值范围是A. x≥－1B. x≤－1C. x≠－1D. x＝－14.下列运算中，正确的是A.x3+x3=x6B. x3·x9=x27C.(x2)3=x5D. x÷x2=x－15.如果点（3，－4）在反比例函数kyx=的图象上，那么下列各点中，在此图象上的是A.（3,4）B. （－2，－6）C.（－2，6）D.（－3，－4）6.下列平面展开图是由5个大小相同的正方形组成，其中沿正方形的边不能．．折成无盖．．小方盒的是AB C D7.⊙O1和⊙O2的半径分别为5和2，O1O2＝3，则⊙O1和⊙O2的位置关系是A.内含B. 内切C.相交D.外切8.下列图形中，是轴对称图形但不是中心对称图形的是A.正三角形B.菱形C.直角梯形D.正六边形9.下列事件中，必然事件是A.抛掷1个均匀的骰子，出现6点向上B.两直线被第三条直线所截，同位角C.366人中至少有2人的生日相同D.实数的绝对值是非负数10.如图，小明随意向水平放置的大正方形内部区域抛一个小球，则小球停在小正方形内部（阴影）区域的概率为A.34B.13C.12D.14二、填空题（每小题3分，共18分.请将答案填写在第Ⅱ卷相应的位置上．．．．．．．．．．．．．．．．）11.因式分解：2x2-8=______▲________12.徐州巿部分医保定点医院2008年第一季度的人均住院费用（单位：元）约为：12 320，11 880,10 370,8 570,10 640, 10240.这组数据的极差是_____▲_______元.13.若12,x x为方程210x x+-=的两个实数根，则12x x+=___▲___.14.边长为a的正三角形的面积等于______▲______.15.如图,AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D.若，若∠C＝18°，则∠CDA＝______▲_______.16.如图，Rt△ABC中，∠B＝90°，AB＝3cm，AC＝5cm，将△ABC折叠，使点C与A重合，得折痕DE，则△ABE的周长等于____▲_____cm.（第10题图）（第15题图）（第16题图）第Ⅱ卷三、解答题（每小题5分，共20分）17.计算：2008011(1)()3π--+-+18.已知21,23.x x x =+--求的值19.解不等式组12215(1)xx x ⎧>-⎪⎨⎪+≥-⎩，并写出它的所有整数解.20.如图，一座堤坝的横截面是梯形，根据图中给出的数据，求坝高和坝底宽（精确到0.1m ）B 1.414B 1.732四、解答题（本题有A 、B 两类题，A 类题4分，B 类题6分，你可以根据自己的学习情况，在两类题中任意选做一题．．．．．．，如果两类题都做，则以A 类题计分） 21.（A 类）已知如图，四边形ABCD 中，AB ＝BC ，AD ＝CD ，求证：∠A ＝∠C.（B 类）已知如图，四边形ABCD 中，AB ＝BC ，∠A ＝∠C ，求证：AD ＝CD.DCBAB（第20题图）（第21题图）五、解答题（每小题7分，共21分）22.从称许到南京可乘列车A 与列车B ，已知徐州至南京里程约为350km ，A 与B 车的平均速度之比为10∶7，A 车的行驶时间比B 车的少1h ，那么两车的平均速度分别为多少？ 23.小王某月手机话费中的各项费用统计情况见下列图表，请你根据图表信息完成下列各题：（1） 该月小王手机话费共有多少元？（2） 扇形统计图中，表示短信费的扇形的圆心角为多少度？ （3）请将表格补充完整； （4） 请将条形统计图补充完整.50403020100项目金额/元24.如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC 的顶点均在格点上，点B 的坐标为（1,0） ①画出△ABC 关于x 轴对称的△A 1B 1C 1，②画出将△ABC 绕原点O 按逆时针旋转90°所得的△A 2B 2C 2，③△A 1B 1C 1与△A 2B 2C 2成轴对称图形吗？若成轴对称图形，画出所有的对称轴；④△A 1B 1C 1与△A 2B 2C 2成中心对称图形吗？若成中心对称图形，写出所有的对称中心的坐标.六、解答题（每小题8分，共16分）25.为缓解油价上涨给出租车待业带来的成本压力，某巿自2007年11月17日起，调整出租车运价，调整方案见下列表格及图像（其中a,b,c 为常数）设行驶路程xkm 时，调价前的运价y 1（元），调价后的运价为y 2（元）如图，折线ABCD 表示y 2与x 之间的函数关系式，线段EF 表示当0≤x ≤3时，y 1与x 的函数关系式，根据图表信息，完成下列各题：①填空：a=______,b=______,c=_______.②写出当x ＞3时，y 1与x 的关系，并在上图中画出该函数的图象.③函数y 1与y 2的图象是否存在交点？若存在，求出交点的坐标，并说明该点的实际意义，若不存在请说明理由.26.已知四边形ABCD 的对角线AC 与BD 交于点O,给出下列四个论断① OA ＝OC ② AB ＝CD ③ ∠BAD ＝∠DCB ④ AD ∥BC请你从中选择两个论断作为条件,以“四边形ABCD 为平行四边形”作为结论,完成下列各题：①构造一个真命题．．．，画图并给出证明； ②构造一个假命题．．．，举反例加以说明.七、解答题（第27题8分，第28题10分，共18分）27.已知二次函数的图象以A （－1，4）为顶点，且过点B （2，－5）①求该函数的关系式；②求该函数图象与坐标轴的交点坐标；③将该函数图象向右平移，当图象经过原点时，A 、B 两点随图象移至A ′、B ′， 求△O A ′B ′的面积.28.如图1，一副直角三角板满足AB ＝BC ，AC ＝DE ，∠ABC ＝∠DEF ＝90°，∠EDF ＝30° 【操作】将三角板DEF 的直角顶点E 放置于三角板ABC 的斜边AC 上，再将三角板．．．．DEF ．．．绕点．．E ．旋转．．，并使边DE 与边AB 交于点P ，边EF 与边BC 于点Q 【探究一】在旋转过程中， （1） 如图2，当CE1EA＝时，EP 与EQ 满足怎样的数量关系？并给出证明. （2） 如图3，当CE2EA＝时EP 与EQ 满足怎样的数量关系？，并说明理由. （3） 根据你对（1）、（2）的探究结果，试写出当CEEA＝m 时，EP 与EQ 满足的数量关系式为_________,其中m 的取值范围是_______(直接写出结论，不必证明)【探究二】若，AC ＝30cm ，连续PQ ，设△EPQ 的面积为S(cm 2)，在旋转过程中：（1） S 是否存在最大值或最小值？若存在，求出最大值或最小值，若不存在，说明理由.（2） 随着S 取不同的值，对应△EPQ 的个数有哪些变化？不出相应S 值的取值范围.徐州巿2008年初中毕业、升学考试数 学 试 题 参 考 答 案1.A2.B3.C4.D5.C6.B7.B8.C9.D 10.C 11. 2(2)(2)x x -+ 12. 3750元 13.－114. 215.126° 16.7cm17.解：原式＝1＋1－3＋2＝118.解：223(3)(1)x x x x --=-+，将1x =+代入到上式，则可得223111)2)1x x --=-+==-F C(E)A(D)Q PDEFCBAQPDEFCBA（图1） （图2） （图3）19.解：12215(1)xx x ⎧>-⎪⎨⎪+≥-⎩222221552x x x x x x >->-⎧⎧⇒⇒-<≤⎨⎨+≥-≤⎩⎩20.解：如图所示，过点A 、D 分别作BC 的垂线AE、DF 分别交BC 于点E 、F ， 所以△ABE、△CDF 均为Rt △，又因为CD ＝14，∠DCF ＝30°，所以DF ＝7＝AE ，且FC ＝B 12.1 所以BC ＝7＋6＋12.1＝25.1m. 21.证明：（A） 连结AC ，因为AB ＝AC ， 所以∠BAC ＝∠BCA ，同理AD ＝CD 得∠DAC ＝∠DCA所以∠A ＝∠BAC ＋∠DAC ＝∠BCA ＋∠DCA ＝∠C （B ）如（A ）只须反过来即可.22.解方程的思想.A 车150km/h ，B 车125km/h. 23.解：（1）125元的总话费 （2）72° （3）（4）BE FDCBA50403020100项目金额/元24. 解：如下图所示， （4）对称中心是（0，0）25.解：(1) a=7, b=1.4, c=2.1 （2）1 2.10.3y x =- （3）有交点为31(,9)7其意义为当317x <时是方案调价前合算，当317x >时方案调价后合算. 26.解：（1）②③为论断时，（2）②④为论断时，此时可以构成一梯形. 27.解：（1）223y x x =--+（2） （0,3），（－3,0），（1,0） （3）略。

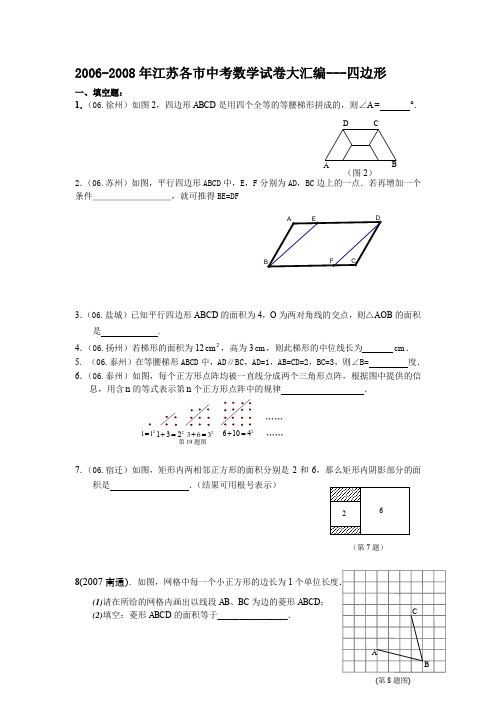
2006-2008年江苏各市中考数学试卷大汇编---四边形一、填空题： 1．（06.徐州）如图2，四边形ABCD 是用四个全等的等腰梯形拼成的，则∠A = °．2．（06.苏州）如图，平行四边形ABCD 中，E ，F 分别为AD ，BC 边上的一点．若再增加一个条件＿＿＿＿＿＿＿＿＿，就可推得BE=DF3．（06.盐城）已知平行四边形ABCD 的面积为4，O 为两对角线的交点，则△AOB 的面积是 .4．（06.扬州）若梯形的面积为122cm ，高为3cm ，则此梯形的中位线长为 cm ． 5. （06.泰州）在等腰梯形ABCD 中，AD ∥BC ，AD=1，AB=CD=2，BC=3，则∠B= 度． 6．（06.泰州）如图，每个正方形点阵均被一直线分成两个三角形点阵，根据图中提供的信息，用含n 的等式表示第n 个正方形点阵中的规律 ．7．（06.宿迁）如图，矩形内两相邻正方形的面积分别是2和6，那么矩形内阴影部分的面积是 ．（结果可用根号表示）8(2007南通)．如图，网格中每一个小正方形的边长为1个单位长度．(1)请在所给的网格内画出以线段AB 、BC 为边的菱形ABCD ； (2)填空：菱形ABCD 的面积等于________________．ABC(第8题图)（第7题）第19题图…… ……211= 2363+= 26104+= 2132+= （图2） AB C D9(2007盐城)．菱形的两条对角线长分别是6和8，则菱形的边长为。

10(2007镇江)．如图，矩形ABCD的对角线相交于O，AB=2，∠AOB=60°，则对角线AC的长为．11(2007镇江)．如图，菱形ABCD的对角线相交于O，AC=8，BD=6，则边AB的长为_______。

12(08常州).若将棱长为2的正方体切成8个棱长为1的小正方体,则所有小正方体的表面积的和是原正方体表面积的_______倍; 若将棱长为3的正方体切成27个棱长为1的小正方体,则所有小正方体的表面积的和是原正方体表面积的_______倍; 若将棱长为n(n>1,且为整数)的正方体切成n3个棱长为1的小正方体,则所有小正方体的表面积的和是原正方体表面积的_______倍.13(08苏州)．将一个边长为1的正八边形补成如图所示的正方形，这个正方形的边长等于 (结果保留根号)．14．（08连云港）如图所示，①中多边形（边数为12）是由正三角形“扩展”而来的，②中多边形是由正方形“扩展”而来的，，依此类推，则由正n边形“扩展”而来的多边形的边数为．①②③④（第14题图）……15．（08淮安）如图，点O （0，0)，B(0，1)是正方形OBB 1C 的两个顶点，以对角线OB 1为一边作正方形OB 1B 2C 1，再以正方形OB 1B 2C 1的对角线OB 2为一边作正方形OB 2B 3C 1，……，依次下去．则点B 6的坐标是________________．16．（08盐城）梯形的中位线长为3，高为2，则该梯形的面积为 ． 17．（08盐城）将一张等边三角形纸片沿着一边上的高剪开，可以拼成不同形状的四边形，试写出其中一种四边形的名称 ．18．（08扬州）如图，在菱形ABCD 中，DE ⊥AB ，垂足为E ，DE=6㎝，sinA=53，则菱形ABCD 的面积是__________㎝2。

徐州市2Q04年初中毕业、升学考试数学试题1．如果收入100元记作+100元，那么支出50元记作_________元．2．我市冬季某一天的最高气温为一l℃，最低气温为一6℃，那么这一天的最高气温比最低气温高_________℃． ，3．函数y=1-x x中自变量x 的取值范围是________________4．当x>l 时，化简2)1(x -=_____________．5．写出一个图象经过点(1，一1)的函数解析式：——． 6．分解因式：x 3y-y 3=_________． 。

7．已知∠α=6300，那么它的余角等于_______度．8．如果等腰三角形的顶角为800，那么它的一个底角为______度．9．在你所学过的几何图形中，写出一个是轴对称图形但不是中心对称图形的图形名称：_______.10．如图，在离地面高度5m 处引拉线固定电线杆，拉线和地面成600角，那么拉线AC 的长约为______m ．(精确到0．1m)11．知圆锥的底面半径是40cm,母线长50cm,那么这个圆锥的侧面积为_______cm 2． 12．如图，AB 为◎o 的直径，弦AC=4cm ，BC=3cm ，CD ⊥AB ，垂足为D ，那么CD 的长为____cm ．二、选择题(本大题共4小题，每小题4分。

共16分)在每小题给出的四个选项中，只有一项是符合题目要求的。

请把正确选项的字母代号填在题后的括号内．13．树叶上有许多气孔，在阳光下，这些气孔一面排出氧气和蒸腾水分，一面吸入二氧化碳，一个气孔在一秒钟内能吸进25000亿个二氧化碳分子．用科学记数法表示25000亿为 ( )A ．2.5×1010B ．2.5×1011C ．2.5×1012 D.25×1011 14．下列边长为a 的正多边形与边长为a 的正方形组合起来，不能镶嵌成平面的是( ) (1)正三角形 (2)正五边形 (3)正六边形 (4)正八边形A.(1)(2) B(2)(3) C(1)(3) D(1)(4)15．顺次连结等腰梯形四边中点得到一个四边形，再顺次连结所得四边形四边的中点得到的图形是 ． ( )A ．等腰梯形B ．直角梯形C ．菱形D ．矩形16．如图，在直角坐标系中，直线y=6-x 与函数y=x4(x>0)的图象相交于点A 、B ，设点A 的坐标为(x 1，，y 1)，那么长为x 1,宽为y 1的矩形面积和周长分别为( ) A ．4，12B ．8，12C ．4，6D ．8,6三、解答题(本大题共5小题，第17、18题每题7分。

2008年江苏省徐州市中考数学试卷
一、选择题（共10小题，每小题2分，满分20分）
1．（2分）（2011•呼伦贝尔）4的平方根是（）
A．±2 B．2 C．﹣2 D．16
2．（2分）（2008•徐州）一方有难、八方支援，截至5月26日12时，徐州巿累计为汶川地震灾区捐款约为11 180万元，该笔善款可用科学记数法表示为（）A．11.18×103万元B．1.118×104万元
C．1.118×105万元D．1.118×108万元
3．（2分）（2010•长沙）函数y=
1
x+1中自变量x的取值范围是（）
A．x≠﹣1 B．x＞﹣1 C．x=﹣1 D．x＜﹣1
4．（2分）（2008•徐州）下列运算中，正确的是（）A．x3+x3=x6B．x3•x9=x27C．（x2）3=x5D．x÷x2=x﹣1
5．（2分）（2008•徐州）如果点（3，﹣4）在反比例函数y=k
x
的图象上，那么下
列各点中，在此图象上的是（）
A．（3，4） B．（﹣2，﹣6）C．（﹣2，6）D．（﹣3，﹣4）
6．（2分）（2008•徐州）下列平面展开图是由5个大小相同的正方形组成，其中沿正方形的边不能折成无盖小方盒的是（）
A．B．C．
D．
7．（2分）（2008•徐州）⊙O1和⊙O2的半径分别为5和2，O1O2=3，则⊙O1和⊙O2的位置关系是（）
A．内含B．内切C．相交D．外切
8．（2分）（2008•徐州）下列图形中，是轴对称图形但不是中心对称图形的是（）A．正三角形B．菱形C．直角梯形D．正六边形。

3927=x x在反比例函数y=，－6）个大小相同的正方形组成，其中沿正方形的边不能A ．正三角形B ．菱形C ．直角梯形D ．正六边形 9．下列事件中，必然事件是（ ） A ．抛掷1个均匀的骰子，出现6点向上 B ．两直线被第三条直线所截，同位角 C ．366人中至少有2人的生日相同 D ．实数的绝对值是非负数10．如图，小明随意向水平放置的大正方形内部区域抛一个 小球，则小球停在小正方形内部（阴影）区域的概率为（ ） A ．34 B ．13 C ．12 D ．14二、填空题（每小题3分，共18分．请将答案填写在第．．．．．．．．Ⅱ．卷相应的位置上．．．．．．．） 11．因式分解：228x -=______▲________12．徐州巿部分医保定点医院2008年第一季度的人均住院费用（单位：元）约为：12 320，11 880，10 370，8 570，10 640， 10240．这组数据的极差是_____▲_______元．13．若12x x ，为方程210x x +-=的两个实数根，则12x x +=___▲___．14．边长为a 的正三角形的面积等于______▲______．15．如图，AB 是⊙O 的直径，点C 在AB 的延长线上，CD 与⊙O 相切于点D ．若，若∠C ＝18°，则CDA ∠=______▲_______．16．如图，Rt ABC △中，∠B ＝90°，AB ＝3cm ，AC ＝5cm ，将△ABC 折叠，使点C 与A 重合，得折痕DE ，则△ABE 的周长等于____▲_____cm ．第Ⅱ卷三、解答题（每小题5分，共20分） 17．计算：1200831(1)π83-⎛⎫-+-+ ⎪⎝⎭．（第10题图）（第15题图）（第16题图）2 1.4143 1.732。

徐州巿2008年初中毕业、升学考试数学试题本试卷分第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷1至2页，第Ⅱ卷3至8页.全卷共120分，考试时间120分钟.第Ⅰ卷注意事项：1.答Ⅰ第卷前考生务必将自己的考试证号、考试科目用2B铅笔填涂在答题卡上.2.作答选择题必须用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动，请用橡皮擦干净后，再选涂其它答案.不能答在第Ⅰ卷上.一、选择题（每小题2分，共20分.在每小题给出的四个选项中，有且只有．．．．一个是正确的）1.4的平方根是A.2± B.2 C. －2 D 162.一方有难、八方支援，截至5月26日12时，徐州巿累计为汶川地震灾区捐款约为11 180万元，该笔善款可用科学记数法表示为A. 11.18×103万元B. 1.118×104万元C. 1.118×105万元D. 1.118×108万元3.函数11yx=+中自变量x的取值范围是A. x≥－1B. x≤－1C. x≠－1D. x＝－14.下列运算中，正确的是A.x3+x3=x6B. x3·x9=x27C.(x2)3=x5D. x÷x2=x－15.如果点（3，－4）在反比例函数kyx=的图象上，那么下列各点中，在此图象上的是A.（3,4）B. （－2，－6）C.（－2，6）D.（－3，－4）6.下列平面展开图是由5个大小相同的正方形组成，其中沿正方形的边不能．．折成无盖．．小方盒的是A B C D7.⊙O 1和⊙O 2的半径分别为5和2，O 1O 2＝3，则⊙O 1和⊙O 2的位置关系是A.内含B. 内切C.相交D.外切 8.下列图形中，是轴对称图形但不是中心对称图形的是A.正三角形B.菱形C.直角梯形D.正六边形 9.下列事件中，必然事件是A.抛掷1个均匀的骰子，出现6点向上B.两直线被第三条直线所截，同位角C.366人中至少有2人的生日相同D.实数的绝对值是非负数10.如图，小明随意向水平放置的大正方形内部区域抛一个小球，则小球停在小正方形内部（阴影）区域的概率为A.34 B. 13 C. 12 D. 14二、填空题（每小题3分，共18分.请将答案填写在第Ⅱ卷相应的位置上．．．．．．．．．．．．．．．．） 11.因式分解：2x 2-8=______▲________12.徐州巿部分医保定点医院2008年第一季度的人均住院费用（单位：元）约为：12 320，11 880,10 370,8 570,10 640, 10240.这组数据的极差是_____▲_______元. 13.若12,x x 为方程210x x +-=的两个实数根，则12x x +=___▲___. 14.边长为a 的正三角形的面积等于______▲______.15.如图,AB 是⊙O 的直径，点C 在AB 的延长线上，CD 与⊙O 相切于点D.若，若∠C ＝18°，则∠CDA ＝______▲_______.16.如图，Rt △ABC 中，∠B ＝90°，AB ＝3cm ，AC ＝5cm ，将△ABC 折叠，使点C 与A 重合，得折痕DE ，则△ABE 的周长等于____▲_____cm.第Ⅱ卷（第10题图）（第15题图）（第16题图）三、解答题（每小题5分，共20分）17.计算：2008011(1)()3π--+-+18.已知21,23.x x x =+--求的值19.解不等式组12215(1)xx x ⎧>-⎪⎨⎪+≥-⎩，并写出它的所有整数解.20.如图，一座堤坝的横截面是梯形，根据图中给出的数据，求坝高和坝底宽（精确到0.1m ）1.4141.732四、解答题（本题有A 、B 两类题，A 类题4分，B 类题6分，你可以根据自己的学习情况，在两类题中任意选做一题．．．．．．，如果两类题都做，则以A 类题计分） 21.（A 类）已知如图，四边形ABCD 中，AB ＝BC ，AD ＝CD ，求证：∠A ＝∠C.（B 类）已知如图，四边形ABCD 中，AB ＝BC ，∠A ＝∠C ，求证：AD ＝CD.五、解答题（每小题7分，共21分）22.从称许到南京可乘列车A 与列车B ，已知徐州至南京里程约为350km ，A 与B 车的平均速度之比为10∶7，A 车的行驶时间比B 车的少1h ，那么两车的平均速度分别为多少？DCBACB（第20题图）（第21题图）23.小王某月手机话费中的各项费用统计情况见下列图表，请你根据图表信息完成下列各题：（1） 该月小王手机话费共有多少元？（2） 扇形统计图中，表示短信费的扇形的圆心角为多少度？ （3） 请将表格补充完整； （4）请将条形统计图补充完整.24.如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点B 的坐标为（1,0） ①画出△ABC 关于x 轴对称的△A 1B 1C 1，短信费长途话费基本话费月功能费50403020100项目金额/元②画出将△ABC 绕原点O 按逆时针旋转90°所得的△A 2B 2C 2，③△A 1B 1C 1与△A 2B 2C 2成轴对称图形吗？若成轴对称图形，画出所有的对称轴；④△A 1B 1C 1与△A 2B 2C 2成中心对称图形吗？若成中心对称图形，写出所有的对称中心的坐标.六、解答题（每小题8分，共16分）25.为缓解油价上涨给出租车待业带来的成本压力，某巿自2007年11月17日起，调整出租车运价，调整方案见下列表格及图像（其中a,b,c 为常数）设行驶路程xkm 时，调价前的运价y 1（元），调价后的运价为y 2（元）如图，折线ABCD 表示y 2与x 之间的函数关系式，线段EF 表示当0≤x ≤3时，y 1与x 的函数关系式，根据图表信息，完成下列各题： ①填空：a=______,b=______,c=_______.②写出当x ＞3时，y 1与x 的关系，并在上图中画出该函数的图象.③函数y1与y2的图象是否存在交点？若存在，求出交点的坐标，并说明该点的实际意义，若不存在请说明理由.26.已知四边形ABCD的对角线AC与BD交于点O,给出下列四个论断①OA＝OC ②AB＝CD ③∠BAD＝∠DCB ④AD∥BC请你从中选择两个论断作为条件,以“四边形ABCD为平行四边形”作为结论,完成下列各题：①构造一个真命题．．．，画图并给出证明；②构造一个假命题．．．，举反例加以说明.七、解答题（第27题8分，第28题10分，共18分）27.已知二次函数的图象以A（－1，4）为顶点，且过点B（2，－5）①求该函数的关系式；②求该函数图象与坐标轴的交点坐标；③将该函数图象向右平移，当图象经过原点时，A、B两点随图象移至A′、B′，求△O A′B′的面积.28.如图1，一副直角三角板满足AB＝BC，AC＝DE，∠ABC＝∠DEF＝90°，∠EDF＝30°【操作】将三角板DEF的直角顶点E放置于三角板ABC的斜边AC上，再将三角板．．．．DEF．．．绕点．．E．旋转．．，并使边DE与边AB交于点P，边EF与边BC于点Q【探究一】在旋转过程中，（1） 如图2，当CE1EA＝时，EP 与EQ 满足怎样的数量关系？并给出证明. （2） 如图3，当CE2EA＝时EP 与EQ 满足怎样的数量关系？，并说明理由. （3） 根据你对（1）、（2）的探究结果，试写出当CEEA＝m 时，EP 与EQ 满足的数量关系式为_________,其中m 的取值范围是_______(直接写出结论，不必证明)【探究二】若，AC ＝30cm ，连续PQ ，设△EPQ 的面积为S(cm 2)，在旋转过程中：（1） S 是否存在最大值或最小值？若存在，求出最大值或最小值，若不存在，说明理由.（2） 随着S 取不同的值，对应△EPQ 的个数有哪些变化？不出相应S 值的取值范围.徐州巿2008年初中毕业、升学考试数 学 试 题 参 考 答 案1.A2.B3.C4.D5.C6.B7.B8.C9.D 10.CF C(E)A(D)Q PDEFCBAQPDEFCBA（图1） （图2） （图3）11. 2(2)(2)x x -+ 12. 3750元 13.－114. 215.126° 16.7cm17.解：原式＝1＋1－3＋2＝118.解：223(3)(1)x x x x --=-+，将1x =代入到上式，则可得223111)2)1x x --=-+==-19.解：12215(1)xx x ⎧>-⎪⎨⎪+≥-⎩222221552x x x x x x >->-⎧⎧⇒⇒-<≤⎨⎨+≥-≤⎩⎩20.解：如图所示，过点A 、D 分别作BC 的垂线AE、DF 分别交BC 于点E 、F ， 所以△ABE 、△CDF 均为Rt △，又因为CD ＝14，∠DCF ＝30°，所以DF ＝7＝AE ，且FC ＝12.1所以BC ＝7＋6＋12.1＝25.1m. 21.证明：（A） 连结AC ，因为AB ＝AC ， 所以∠BAC ＝∠BCA ，同理AD ＝CD 得∠DAC ＝∠DCA所以∠A ＝∠BAC ＋∠DAC ＝∠BCA ＋∠DCA ＝∠C （B ）如（A ）只须反过来即可.22.解方程的思想.A 车150km/h ，B 车125km/h. 23.解：（1）125元的总话费 （2）72° （3）（4）CBE FDCBA50403020100金额/元24. 解：如下图所示，（4）对称中心是（0，0）25.解：(1) a=7, b=1.4, c=2.1（2）12.10.3y x =-（3）有交点为31(,9)7其意义为当317x<时是方案调价前合算，当317x>时方案调价后合算.26.解：（1）②③为论断时，（2）②④为论断时，此时可以构成一梯形.27.解：（1）223y x x=--+（2）（0,3），（－3,0），（1,0）（3）略。