0_博弈论

一、双人零和博弈的概念零和博弈又称零和游戏，与非零和博弈相对，是博弈论的一个概念，属非合作博弈，指参与博弈的各方，在严格竞争下，一方的收益必然意味着另一方的损失，一方收益多少，另一方就损失多少，所以博弈各方的收益和损失相加总和永远为“零”.双方不存在合作的可能.用通俗的话来讲也可以说是:自己的幸福是建立在他人的痛苦之上的，二者的大小完全相等，因而双方在决策时都以自己的最大利益为目标，想尽一切办法以实现“损人利己”.零和博弈的结果是一方吃掉另一方，一方的所得正是另一方的所失，整个社会的利益并不会因此而增加一分.二、双人零和博弈的模型的建立建立双人零和博弈的模型，就是要根据对实际问题的叙述确定参与人（局中人）的策略集以及相应的收益矩阵（支付矩阵）.我们记双人零和博弈中的两个局中人为A和B;局中人A的策略集为a1,…,am,局中人B的策略集为b1,…,bn;cij为局中人A采取策略ai、局中人B采取策略bj 时A的收益（这时局中人B的收益为- cij）.则收益矩阵见下表表1那么下面我们通过例子来说明双人零和博弈模型的建立: 例1甲、乙两名儿童玩猜拳游戏.游戏中双方同时分别或伸出拳头（代表石头）、或手掌（代表布）、或两个手指（代表剪刀）.规则是剪刀赢布，布赢石头，石头赢剪刀，赢者得一分.若双方所出相同，算和局，均不得分.试列出对儿童甲的赢得矩阵.解 本例中儿童甲或乙均有三个策略:或出拳头，或出手掌，或出两个手指，根据例子中所述规则，可列出对儿童甲的赢得矩阵见表2.表2例2 从一张红牌和一张黑牌中随机抽取一张，在对B 保密情况下拿给A 看，若A 看到的是红牌，他可选择或掷硬币决定胜负，或让B 猜.若选择掷硬币，当出现正面，A 赢p 元，出现反面，输q 元;若让B 猜，当B 猜中是红牌，A 输r 元，反之B 猜是黑牌，A 赢s 元.若A 看到的是黑牌，他只能让B 猜.当B 猜中是黑牌，A 输u 元，反之B 猜是红牌，A 赢t 元，试确定A 、B 各自的策略，建立支付矩阵.解 因A 的赢得和损失分别是B 的损失和赢得，故属二人零和博弈.为便于分析，可画出如图3的博弈树图.图3中，○为随机点，□分别为A 和B 的决策点，从图中看出A 的策略有掷硬币和让B 猜两种，B 的策略有猜红和猜黑两种，据此可归纳出各种情况下A 和B 输赢值分析的表格，见表4.图3抽到红牌正面反面抽到黑球○□□○□1/2掷硬币让B 猜1/21/2猜红猜黑猜黑猜红1/2让B 猜p-q-rst-u表4对表4中各栏数字可以这样来理解:因让A 看到红牌时或掷硬币或让B 猜.若A 决定选掷硬币这个策略，当出现正面，这时不管B 猜红或猜黑，A 都赢p 元;当出现反面，不管B 猜红或猜黑，A 都输q 元.同样A 选择让B 猜的策略后，他的输赢只同B 猜红或猜黑有关，而与掷硬币的正反面无关.又若抽到的牌是黑牌，A 的决定只能让B 猜，因而掷硬币策略对A 的胜负同样不起作用.考虑到抽牌时的红与黑的概率各为1/2，掷硬币时出现正反面的概率也各为1/2,故当A 采取“掷硬币”策略，而B 选择“猜红”策略时，A 的期望赢得为:⎪⎭⎫ ⎝⎛-q p 212121+t 21=()t q p 241+- 当A 采取让B 猜策略，B 选择“猜红”策略时，A 的期望赢得为:()()⎪⎭⎫ ⎝⎛-+-r r 212121+t 21=()t r +-21 相应可求得其他策略对A 的期望赢得值.由此可列出本例的收益矩阵，见表5.表5三、双人零和博弈的求解定理1（极小极大定理）在零和博弈中，对于给定的支付矩阵U ，如果存在混合战略1σ*=（1σ*1，…1σ*m ）和2σ*=（2σ*1，…2σ*n ）以及一个常数v 满足，对任意j 有∑=mi i ij a 11*σ≥v ，对任意的i 有∑=nj j ij a 12*σ≤v ，那么战略组合（1σ*，2σ*）为该博弈的Nash 均衡.其中，v 为参与人1在均衡中所得到的期望支付，亦称该博弈的值.这个极小极大定理，其基本思想就是:参与人1考虑到对方使自己支付最小的最优反应，从中选择使自己最好的策略.参与人2也遵循同样的思路，这样才能满足Nash 均衡的互为最优反应的条件.这样我们就可以得到双人零和博弈Nash 均衡的计算方法了，如以下定理定理2 对于给定的零和博弈，如果博弈的值v 大于0，则博弈的Nash 均衡（1σ*，2σ*）为以下对偶线性规划问题的解Min ∑=mi i p 1s.t. ∑=mi i ij p a 1≥1 (j=1,…,n)i p ≥0 (i=1,…,m) 和Max ∑=nj j q 1s.t. ∑=nj j ij q a 1≤1 (i=1,…,m)j q ≥0 (j=1,…,n) 其中，Nash 均衡支付∑∑====nj jmi iqpv 1111Nash 均衡战略),,,,(1*1m i vp vp vp =σ，),,,(1*2n j vq vq vq =σ由于此定理只适用于v 大于0的情形，因此对于v 小于等于0的情形，该定理所给出的方法需做适当的修改.命题 如果支付矩阵U=mxn ij a )(的每个元素都大于0,即ij a ＞0,那么博弈的值大于0,即v ＞0.定理3 如果支付矩阵U '=mxn ij a )('是由U=mxn ij a )(的每个元素都加上一个常数c 得到，即c a a ij ij +='，那么支付矩阵U 和U '所对应的零和博弈的Nash 均衡战略相同，博弈的值相差c.根据以上定理，可以得到如下求解一般零和博弈Nash 均衡的方法:(1) 若支付矩阵U 中的所有元素都大于零，则可以直接根据定理进行计算;若支付矩阵U 中有小于0的元素,可以通过加上一个常数使它们都大于0,然后再根据定理进行计算. (2) 求解定理中的两个对偶线性规划问题.下面通过实例来说明如何求解双人零和博弈的Nash 均衡.例3 求解下图中战略式博弈的Nash 均衡. 参与人2L M RU参与人1 C D通过求解对偶线性规划问题求零和博弈的Nash 均衡解 根据前面的介绍，可知该博弈的支付矩阵为U=⎪⎪⎪⎭⎫ ⎝⎛224132312不难发现，该博弈的支付矩阵U=()33x ij a 的每个元素都大于0，即ij a >0,那么博弈的值大于0，即v>0.设参与人1和参与人2的混合战略分别是1σ=（321,,vp vp vp ）和2σ=（321,,vq vq vq ）,利用对偶线性规划求解方法求解该战略式博弈的Nash 均衡，构造规划问题如下.Min ｛321p p p ++｝s.t. 321422p p p ++≥1 32123p p p ++≥1 32123p p p ++≥1 1p ≥0,2p ≥0,3p ≥0 和Max ｛321q q q ++｝s.t. 32132q q q ++≤1 32132q q q ++≤1 321224q q q ++≤1 1q ≥0,2q ≥0,3q ≥0求解第一个规划问题，得到1p =1/4, 2p =1/4, 3p =0,参与人1的支付v=2.因此，参与人1的混合战略1σ*=（1/2,1/2,0）.同理，对对偶问题求解，得到1q =0，2q =1/4, 3q =1/4,参与人2的损失v=2,因此参与人的混合战略2σ*=（0,1/2,1/2）.所以，该博弈存在一个混合战略Nash 均衡（（1/2,1/2,0）（0,1/2,1/2），）.例4 求解下图中的战略式博弈的Nash 均衡.参与人2L M R U 参与人1 C D通过求解对偶线性规划问题求零和博弈的Nash 均衡解 该博弈的支付矩阵为U=⎪⎪⎪⎭⎫ ⎝⎛--203011122 在上树支付矩阵U=33)(x ij a 中，12a <0, 21a <0.为了利用对偶线性规划模型求解博弈的解，构造支付矩阵U '=33')(x ij a ,其中a 'ij=ij a +c.令c=2，那么新构造的支付矩阵为U '=⎪⎪⎪⎭⎫ ⎝⎛425231304 设参与人1和参与人2的混合战略分别是1σ=（v 'p 1, v 'p 2, v 'p 3）和2σ=（v 'q 1, v 'q 2 v 'q 3,）,v 为原博弈的值，v '为新博弈的值，且v '=v+2，利用对偶线性规划求解方法求解新战略式博弈的Nash 均衡，构造规划问题如下.Min ｛321p p p ++｝ s.t. 32154p p p ++≥13223p p +≥1 321423p p p ++≥11p ≥0, 2p ≥0, 3p ≥0Max ｛321q q q ++｝s.t. 3134q q +≤1 32123q q q ++≤1 321425q q q ++≤1 1q ≥0,2q ≥0,3q ≥0通过求解对偶问题，得到1p =0，2p =3/13, 3p =2/13,参与人1的支付v '=13/5, 1q =1/13, 2q =4/13, 3q =0,参与人2的损失v '=13/5.因此，参与人1的混合战略1σ*=（0,3/5,2/5）, 参与人2 的混合战略2σ*=(1/5,4/5,0)，原博弈的值v= v '-2=3/5.所以，博弈存在一个混合战略Nash 均衡（（0,3/5,2/5），(1/5,4/5,0)）.。

0 序言0.1 博弈论的产生博弈论（game theory)又称对策论，是由美国数学家冯·诺依曼(Von. Neumann)和经济学家摩根斯坦(Morgenstern)于1944年创立的带有方法论性质的学科，是一种处理竞争与合作问题的数学决策方法。

它既是现代数学的一个新分支，也是运筹学的一个重要学科。

目前在经济学、国际关系学、计算机科学、政治学、生物学、军事战略和其他很多学科都有广泛的应用。

0.2 博弈论的发展0.2.1博弈理论的早期研究一般认为，对于博弈理论的最早研究可以追溯到18世纪初。

瓦德格拉夫（Waldegrave）在1713年提出了两人博弈的极小化极大混合策略解。

古诺（Cournot）和伯特兰德(Bertrand)分别在1838年和1883年提出了博弈论最经典的模型，两位学者分别从产量决策和价格决策分析垄断的双寡头竞争模型，确定了在竞争之下各自的最优反映函数。

这些都是关于博弈问题的早期的零星研究。

0.2.2博弈论发展的不同阶段（1）一般认为博弈论萌芽于20世纪初。

1913年齐默罗(Zermelo)提出的“逆推归纳法”(Backward Induction Procedure)是博弈论的第一种有着一般意义的分析方法。

博弈论创立的标志是冯·诺伊曼和摩根斯坦在1944年的《博弈论与经济行为》这部著作。

在该著作中，引进了博弈论的扩展形(Extensive Form)和策略形(Strategy)表示方式，提出了创建博弈论的基本概念术语，并对合作博弈进行了研究。

（2）20世纪的40年代末到50年代初，是博弈论的发展史上一个重要阶段。

越来越多的学者进行了博弈理论的研究。

1950年，纳什（John Nash）在他的博士论文《非合作博弈》中，将博弈论扩展到了非零和博弈，最终形成了非合作博弈理论的思想源泉，纳什均衡概念的提出以及纳什均衡存在性的纳什定理的证明，发展了以纳什均衡概念为核心的非合作博弈理论。

零和博弈零和博弈又称“零和游戏”，是博弈论的一个概念，属非合作博弈，指参与博弈的各方，在严格竞争下，一方的收益必然意味着另一方的损失，博弈各方的收益和损失相加总和永远为“零”。

双方不存在合作的可能。

零和博弈的结果是一方吃掉另一方，一方的所得正是另一方的所失，整个社会的利益并不会因此而增加一分。

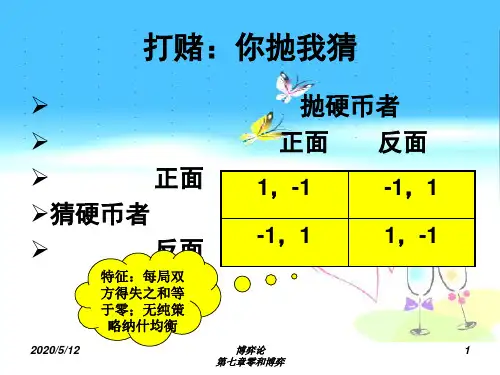
零和博弈简介当你看到两位对弈者时，你就可以说他们正在玩“零和游戏”。

因为在大多数情况下，总会有一个赢，一个输，如果我们把获胜计算为得1分，而输棋为-1分，那么，这两人得分之和就是：1+（-1）=0。

这正是“零和游戏”的基本内容：游戏者有输有赢，一方所赢正是另一方所输，游戏的总成绩永远是零。

零和游戏原理之所以广受关注，主要是因为人们发现在社会的方方面面都能发现与“零和游戏”类似的局面，胜利者的光荣后面往往隐藏着失败者的辛酸和苦涩。

从个人到国家，从政治到经济，似乎无不验证了世界正是一个巨大的“零和游戏”常这种理论认为，世界是一个封闭的系统，财富、资源、机遇都是有限的，个别人、个别地区和个别国家财富的增加必然意味着对其他人、其他地区和国家的掠夺，这是一个“邪恶进化论”式的弱肉强食的世界。

但20世纪人类在经历了两次世界大战，经济的高速增长、科技进步、全球化以及日益严重的环境污染之后，“零和游戏”观念正逐渐被“双赢”观念所取代。

人们开始认识到“利己”不一定要建立在“损人”的基础上。

通过有效合作，皆大欢喜的结局是可能出现的。

但从“零和游戏”走向“双赢”，要求各方要有真诚合作的精神和勇气，在合作中不要耍小聪明，不要总想占别人的小便宜，要遵守游戏规则，否则“双赢”的局面就不可能出现，最终吃亏的还是自己。

零和博弈的例子一、零和博弈首先来明确定义。

毫无疑问期货交易是一种零和博弈，因为：输家损失＝赢家收益＋交易成本（市场运行成本、信息成本等）而在股票市场要获得资金等式的平衡，除了以上各项外，还要把上市公司的融资（资金从股市流出）和现金分红（资金流入股市）考虑在内。