转角计算

单自由度系统是指一个只有一个自由度的系统，通常用来描述某一特定物体或结构在运动或受力下的行为。

支座转角是指支座在承受荷载时所发生的转动变形，对于单自由度系统而言，支座转角通常是一个重要的参数。

在工程实践中，计算支座转角的公式是非常重要的，可以帮助工程师和设计师准确地预测结构的变形和稳定性。

1.1 支座转角的意义支座转角是结构工程中常用的一个参数，它可以用来描述结构在受力下的变形情况。

通过计算支座转角，工程师可以评估结构的稳定性、安全性和使用性能，为结构的设计和施工提供重要参考。

另外，在地震、风荷载等外部环境作用下，支座转角的计算也是评估结构抗震性能和风荷载性能的重要手段。

1.2 支座转角的计算公式支座转角的计算公式是基于结构力学和材料力学原理的推导和假设得出的。

对于单自由度系统而言，其支座转角的计算公式可以通过以下步骤推导得出：步骤一：确定系统的自由度单自由度系统只有一个自由度，通常可以用一个参数来描述系统的位移或转角。

在计算支座转角时，需要先确定系统的自由度，并选取适当的坐标系和参考点。

步骤二：建立受力平衡方程根据结构所受的外部荷载和内部反力，建立结构的受力平衡方程。

步骤三：建立结构的变形方程根据结构所受的荷载和材料的力学性质，建立结构的变形方程。

通常可以通过弹性力学理论或位移法来建立结构的变形方程。

步骤四：求解支座转角通过联立受力平衡方程和变形方程，可以解得支座转角的计算公式。

通常需要考虑结构的几何形状、材料性质、截面性质、边界条件等因素，得出支座转角的表达式。

1.3 支座转角的影响因素支座转角的计算和预测受到多种因素的影响，主要包括以下几个方面：材料性质：结构所用的材料的弹性模量、泊松比等材料性质对支座转角的影响较大。

截面形状：结构的截面形状、尺寸和几何形状对支座转角的影响较大，通常需要考虑截面的截面积、惯性矩、截面形心等因素。

荷载类型：结构所受的外部荷载类型、大小和作用位置对支座转角的影响较大，通常需要考虑静载荷、动载荷、温度荷载等不同类型的荷载。

挠度和转角计算公式
《挠度和转角计算公式》
挠度(sag)和
1、挠度的定义：
挠度(sag)是指弹性体经受内力时形变的程度，也可以定义为弹性体在受力后，其形状发生的偏移量。

2、挠度的计算公式
挠度的计算公式为：挠度S=F×L/E×I，其中，F为外力，L为梁的长度，E为梁的弹性模量，I为梁的惯性矩。

3、转角的定义
转角(twist angle)指的是当被施加外力时，弹性体的一端相对于另一端转动的角度。

4、转角的计算公式
转角的计算公式为：转角α=F×L/G×J，其中，F为外力，L为梁的长度，G为梁的刚度系数，J为梁的惯性矩。

- 1 -。

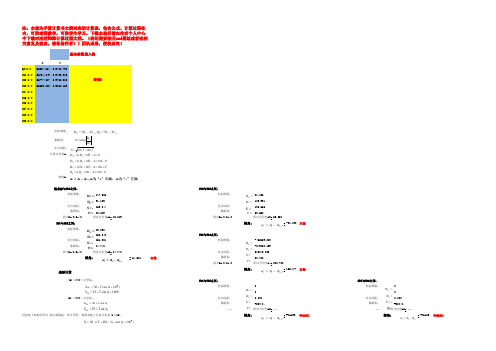
XY QD(X,Y)455507.264249408.796JD1(X,Y)455754.849249499.985JD2(X,Y)455777.887249750.228JD3(X,Y)455859.083249860.159JD4(X,Y)JD5(X,Y)JD6(X,Y)JD7(X,Y)JD8(X,Y)JD9(X,Y)247.58581.19691.189109.931263.844136.66620.21953.55020.21953.550-31.190左偏23.038250.243251.301-455859.08384.740-249860.15984.740519843.82564.521右偏28.728208.728155.177右偏0.0000.000#DIV/0!#DIV/0!!!!!!!#VALUE!#VALUE!#VALUE!#VALUE!所以方位角A6=转角：=JD5与JD6之间：坐标增量：交点间距：象限角：!!!所以方位角A4=转角：=所以方位角A5=坐标增量：转角：=设直线上加桩里程为 表示曲线起、终点里程，则前直线上任意点坐标(L≤ZH)：JD4与JD5之间：所以方位角A3=转角：=JD3与JD4之间：JD2与JD3之间：坐标增量：交点间距：象限角：因为Dx>0,Dy>0!!!交点间距：象限角：因为Dx<0,Dy<0转角a坐标增量：象限角：HZ（或YZ）点坐标：JD1与JD2之间：坐标增量：交点间距：象限角：因为Dx>0,Dy>0所以方位角A2=转角：=坐标计算ZH（或ZY）点坐标：转角a：交点间距：起点QD与JD1之间：坐标增量：交点间距：象限角：因为Dx>0,Dy>0所以方位角A1=象限角：注：本表为手算计算书文档对应的计算表，包含公式、计算过程在内，可供老师教学，可供学生学习。

下载本表后请在作者个人中心中下载对应的WORD计算过程文档。

直线曲线转角表1. 背景介绍直线曲线转角表是用来记录并展示直线和曲线转角的工具。

在工程设计、建筑规划、道路运输等领域中，我们常常需要计算和确定两个物体之间的转角，以确保设计和运输的顺利进行。

直线曲线转角表可以帮助我们快速准确地计算和查找转角数值，提高工作效率。

2. 直线曲线转角的概念直线曲线转角指的是两条线段或曲线之间的夹角。

直线转角通常是两条直线的夹角，而曲线转角则是两条曲线的夹角。

直线曲线转角的数值通常以角度来表示，常用单位有度（°）和弧度（rad）。

直线曲线转角在许多领域中都有着重要的应用。

3. 直线曲线转角的计算方法3.1 直线转角的计算方法直线转角的计算方法相对简单，可以通过几何图形的性质来推导得出。

对于两条直线之间的转角，我们可以利用向量的内积公式求解。

设直线的方向向量分别为A和B，则两条直线的夹角θ满足以下公式：cos(θ) = (A·B) / (|A||B|) 其中，A·B表示向量A和向量B的内积，|A|和|B|分别表示向量A和向量B的模。

通过求解这个公式，即可得到直线转角的数值。

3.2 曲线转角的计算方法曲线转角的计算方法相对复杂，需要根据具体的曲线类型采用不同的计算方法。

对于圆弧和二次曲线来说，曲线转角可以通过弧长和半径之间的关系来计算。

设圆弧或二次曲线的半径为R，弧长为D，则曲线转角θ满足以下公式：θ = D / R 对于其他类型的曲线，计算方法可能会有所不同，需要根据具体情况进行推导和计算。

4. 直线曲线转角表的使用方法4.1 转角表的结构直线曲线转角表一般以表格的形式呈现，列出不同情况下的直线和曲线转角数值。

常见的表格结构包括起点、终点、转角角度等列。

4.2 使用方法使用直线曲线转角表时，需要根据具体的情况找到对应的转角数值。

以直线为例，可以通过查找起点和终点的坐标在转角表中找到对应的直线转角数值。

对于曲线转角，需要知道曲线的类型和特征参数，然后在转角表中找到相应的曲线转角数值。

管子先焊后弯法兰预转角的计算及施工方法引言：在工程建设中，管道系统是不可或缺的一部分。

而对于一些需要曲线或转角的管道布局，使用先焊接管子再进行弯管的方法是常见的施工方式之一。

本文将重点介绍管子先焊后弯法兰预转角的计算及施工方法，旨在帮助施工人员更好地理解和掌握这一技术。

一、管子先焊后弯法兰预转角的计算方法1. 收集必要的参数数据在进行管子先焊后弯法兰预转角的计算之前，首先需要收集以下数据：- 弯管的内径（D）- 弯管的外径（d）- 弯曲半径（R）- 预期转角（θ）2. 计算转角补偿长度（Lc）根据预期转角和弯曲半径，可以使用以下公式计算出转角补偿长度（Lc）：Lc = R * θ * π / 1803. 计算弯装长度（Lb）弯装长度（Lb）是管子在进行弯曲前，受到附加长度的补偿值。

可以使用以下公式计算弯装长度（Lb）：Lb = Lc * (D+d) / (2 * D)4. 计算管子总长度（Lt）管子总长度（Lt）是管子在进行弯曲后的最终长度。

可以使用以下公式计算管子总长度（Lt）：Lt = Lb + 2 * R * sin(θ * π / 360)二、管子先焊后弯法兰预转角的施工方法1. 准备工作在施工之前，需要进行以下准备工作：- 确保弯管及附件的质量可靠。

- 清理工作区，确保周围环境干净无障碍。

- 检查焊接设备的工作状态，确保焊接质量。

2. 进行预转角计算根据前文所述的计算方法，计算出管子先焊后弯法兰的预转角。

3. 进行焊接将管子的两端与对应的法兰焊接在一起。

在焊接过程中，确保焊接质量稳定可靠。

4. 进行弯曲使用专业的弯管机或另外的工具，在焊接点的相对位置进行弯曲。

在进行弯曲时，注意保持转角的一致性和精确度。

5. 检查和处理完成弯曲后，对焊接部位进行检查，确保焊接质量符合要求。

如果发现有任何问题，需要及时进行处理。

6. 清理和整理清理工作区，将废弃物和工具进行整理和归类。

结论：管子先焊后弯法兰预转角是一种常用的施工方法，可以应用于需要弯曲的管道系统布局中。

90度转角系数1.37 -回复90度转角系数是指在道路设计和规划中，曲线的转弯角度与曲线半径之间的关系。

它是设计流线型道路的重要参数之一，旨在提高道路的安全性和通行效率。

本文将一步一步回答关于90度转角系数的问题，详细解释其含义和应用。

首先，我们需要了解什么是转角系数。

转角系数是指曲线转弯角度和曲线半径之间的比值。

对于90度转角系数来说，它表示在曲线的转弯角度为90度时，曲线的半径与曲线长度之间的比值。

接下来，我们需要明白为什么90度转角系数对道路设计和规划非常重要。

在道路规划中，通过合理的曲线设计可以提高道路的安全性和通行效率。

而90度转角系数可以帮助工程师确定合适的曲线半径，从而确保车辆可以顺利通过道路的转弯处，避免发生交通事故。

然后，让我们进一步讨论90度转角系数的计算方法。

一般来说，转角系数可以通过以下公式来计算：转角系数= 曲线半径/ 曲线长度对于90度转角系数来说，转角系数为1.37。

这意味着在转弯角度为90度时，曲线的半径应为曲线长度的1.37倍。

这个数值可以帮助工程师确定合适的曲线半径，以确保车辆在转弯时能够保持稳定，并且能够有效地驾驶。

进一步讨论90度转角系数的应用。

在实际的道路设计和规划中，90度转角系数可以作为参考指标来确定道路转弯处的半径。

例如，在城市中心的拐角处，通常会有90度的转弯。

通过使用90度转角系数，工程师可以根据道路的设计速度和车辆的需求，并考虑到安全因素，确定合适的转弯半径，确保车辆能够平稳地通过拐角处。

此外，90度转角系数还可以用于评估现有道路的设计是否合理。

如果90度转角系数超过了1.37，说明转弯半径太小，这可能导致车辆在转弯时安全性下降，甚至发生交通事故。

相反，如果90度转角系数小于1.37，说明转弯半径太大，可能浪费了宝贵的道路空间。

因此，根据90度转角系数的计算结果，工程师可以调整和优化道路设计，以达到更好的安全性和通行效率。

总结一下，90度转角系数在道路设计和规划中起着重要的作用。

等效转轴与等效转角的计算公式在机械设计中，经常需要计算旋转物体的转动惯量、角加速度、角速度等参数。

而在实际应用中，往往需要将旋转物体的运动转化为平移运动，或者将平移运动转化为旋转运动。

这时，就需要用到等效转轴和等效转角的概念。

一、等效转轴等效转轴是指将一个物体的转动惯量、角加速度、角速度等参数，转化为绕一个虚拟的轴旋转的情况下，所需要的转动惯量、角加速度、角速度等参数。

这个虚拟的轴就是等效转轴。

等效转轴的计算公式如下：设物体的转动惯量为I，绕一个距离为r的轴旋转，则其转动惯量为I1，根据斯蒂诺定理可得：I1 = I + mr^2其中，m为物体的质量。

如果将物体绕一个距离为r1的轴旋转，则其转动惯量为I2，根据斯蒂诺定理可得：I2 = I + mr1^2将上述两个式子相减，可得：I2 - I1 = m(r1^2 - r^2)将上述式子变形，可得：r1 = sqrt(r^2 + (I2 - I1)/m)这个距离r1就是等效转轴的位置。

二、等效转角等效转角是指将一个物体的旋转角度，转化为绕一个虚拟的轴旋转的情况下，所需要的旋转角度。

这个虚拟的轴就是等效转轴。

等效转角的计算公式如下：设物体绕一个距离为r的轴旋转了一个角度θ，则其等效转角为θ1，根据正弦定理可得：sin(θ/2) = (L/2)/r其中，L为物体的长度。

如果将物体绕一个距离为r1的轴旋转，则其等效转角为θ2，根据正弦定理可得：sin(θ1/2) = (L/2)/r1将上述两个式子相除，可得：sin(θ2/2)/sin(θ1/2) = r1/r将上述式子变形，可得：θ2 = 2arcsin[(r1/r)sin(θ/2)]这个角度θ2就是等效转角。

三、应用举例1. 计算等效转轴假设一个质量为2kg的物体，绕一个距离为10cm的轴旋转，其转动惯量为0.1kg·m²。

现在需要将其转化为绕一个等效转轴旋转的情况下，所需要的距离。

注：本文档为手算计算书文档，包含公式、计算过程在内，可供老师教学，可供学生学习。

下载本文档后请在作者个人中心中下载对（若还需要相关cad图纸或者有相关意见及建议，应Excel计算过程。

请私信作者！）团队成果，侵权必究！（温馨提示，本文档没有计算功能，请在作者个人中心中下载对应的Excel计算表格，填入基本参数后，Excel表格会计算出各分项结果，并显示计算过程！）路线长度及方位角的计算设计线形大致如下图所示:平面交点坐标表交点 XY起点 4671934.963 510224.512 JD1 4672536.121 509797.516 JD2 4673116.256 508735.406 JD3 4674086.362 508426.647 JD4 4674757.379 508525.444 JD5 4675701.954 509279.022 JD6 4676647.217 508589.671 终点4677843.309508676.580（1）路线交点间距及方位角的计算： AB 段长度：坐标增量： 11,---=-=i i Y i i X YJ YJ D XJ XJ D象限角： XY D Da r c t g =θ交点间距： ()()22Y X D D S +=计算方位角A ：θ=>>A D D Y X 时，0,0 θ-=><1800,0A D D Y X 时，θ+=<<1800,0A D D Y X 时， θ-=<>3600,0A D D Y X 时，转角”左偏为“”右偏，为“-+-=-i i i i i A A ααα,1 起点QD 与JD 1之间：坐标增量： 交点间距： 象限角：因为x D ＞0，y D ＜0，故方位角JD1与JD2之间：坐标增量：交点间距：象限角：因为D＞0，y D＜0，故方位角x转角：左偏即JD2与JD3之间：坐标增量：交点间距：象限角：因为D＞0，y D＜0，故方位角x转角：（右偏）即JD3与JD4之间：坐标增量：交点间距：象限角：因为D＞0，y D＞0，故方位角x转角：（左偏）或右偏，即JD3与JD4之间：坐标增量：交点间距：象限角：因为D＞0，y D＞0，故方位角x转角：（左偏）或右偏，即JD4与JD5之间：坐标增量：交点间距：象限角：因为D＞0，y D＞0，故方位角x转角：右偏即JD5与JD6之间：坐标增量：交点间距：象限角：因为D＞0，y D＜0，故方位角x转角：（右偏）或左偏，即JD6与ZD之间：坐标增量：交点间距：象限角：因为D＞0，y D＞0，故方位角x转角：（左偏）或右偏，即路线转角计算左偏（右偏）（左偏）或右偏(右偏)(左偏)(右偏)。

橱柜转角重叠部分计算公式橱柜是厨房中不可或缺的家具，它可以帮助我们储存食品、炊具和餐具，让厨房更加整洁和有序。

然而，在安装橱柜的过程中，我们经常会遇到一个问题，那就是橱柜的转角重叠部分该如何计算。

本文将介绍橱柜转角重叠部分的计算公式，帮助大家更好地安装橱柜。

橱柜转角重叠部分的计算公式可以帮助我们准确地确定橱柜的尺寸，确保橱柜的安装和使用都更加方便和合理。

在计算橱柜转角重叠部分之前，我们首先需要了解一些相关的概念和术语。

橱柜的转角是指两个相邻橱柜的连接处，通常是一个90度的角。

在转角处，橱柜的尺寸会有所重叠，这样可以确保橱柜之间没有间隙，使得整个厨房更加美观和实用。

而橱柜的重叠部分则是指两个相邻橱柜的重叠部分，通常是一个橱柜的侧板和另一个橱柜的前板之间的重叠部分。

在计算橱柜转角重叠部分时，我们需要考虑两个方面的因素，即橱柜的尺寸和安装的方式。

首先，我们需要测量橱柜的尺寸，包括长度、宽度和高度，然后根据实际情况确定橱柜的安装方式，包括橱柜的安装位置和连接方式。

在计算橱柜转角重叠部分时，我们可以使用以下的计算公式：重叠部分 = 橱柜长度转角直线距离。

其中，橱柜长度是指橱柜的实际长度，转角直线距离是指两个相邻橱柜连接处的直线距离。

通过这个计算公式，我们可以准确地计算出橱柜转角重叠部分的尺寸，从而更好地安装橱柜。

在实际操作中，我们还需要考虑到橱柜的安装方式和连接方式。

通常情况下，橱柜的连接方式有两种，一种是直角连接，另一种是斜角连接。

在直角连接的情况下，转角直线距离可以通过勾股定理来计算，即转角直线距离的平方等于两个相邻橱柜的长度的平方之和。

而在斜角连接的情况下，转角直线距离则需要根据实际情况来确定。

除了计算橱柜转角重叠部分的尺寸之外，我们还需要考虑到橱柜的安装位置和连接方式。

在安装橱柜时，我们需要确保橱柜之间没有间隙，同时还需要考虑到橱柜的开合和使用方便性。

因此，在计算橱柜转角重叠部分时，我们还需要考虑到这些因素，确保橱柜的安装更加合理和方便。

窗帘轨道转角弧度计算公式窗帘轨道转角弧度是指窗帘轨道在转角处的弧度值，它是计算窗帘轨道在转角处的曲线运动所必需的重要参数。

在窗帘安装过程中，经常会遇到需要在转角处安装窗帘轨道的情况，因此准确计算转角处的弧度值对于窗帘的安装和使用至关重要。

窗帘轨道转角弧度计算公式可以通过几何和三角函数的知识来推导。

首先，我们需要知道窗帘轨道在转角处的长度和转角的大小，然后通过三角函数来计算出转角处的弧度值。

假设窗帘轨道在转角处的长度为L，转角的大小为θ，我们可以利用三角函数的知识来计算出转角处的弧度值。

根据三角函数的定义，正弦函数sinθ等于对边与斜边的比值，而余弦函数cosθ等于邻边与斜边的比值。

因此，我们可以利用这些关系来计算出转角处的弧度值。

具体的计算公式如下：弧度值 = 弧长 / 半径。

其中，弧长可以通过窗帘轨道在转角处的长度L来表示，而半径则可以通过转角的大小θ来表示。

因此，窗帘轨道转角处的弧度计算公式可以表示为：弧度值 = L / θ。

通过这个公式，我们可以很容易地计算出窗帘轨道在转角处的弧度值。

在实际操作中，我们可以先测量窗帘轨道在转角处的长度L，然后再测量转角的大小θ，将这些数值代入公式中进行计算，就可以得到转角处的弧度值。

需要注意的是，转角处的弧度值是一个重要的参考数值，它可以帮助我们更好地安装和调整窗帘轨道，确保窗帘在转角处的运动轨迹是流畅和稳定的。

因此，在实际操作中，我们需要尽量准确地测量窗帘轨道在转角处的长度和转角的大小，确保计算出的弧度值是准确的。

除了窗帘轨道转角处的弧度计算公式外，我们还可以通过其他方法来计算出转角处的弧度值。

例如，我们可以利用数学软件进行计算，通过输入窗帘轨道在转角处的长度和转角的大小，软件可以自动计算出转角处的弧度值。

这种方法可以提高计算的准确性和效率，特别是在复杂的情况下，可以更好地满足实际需求。

总之，窗帘轨道转角弧度计算公式是一个重要的工具，它可以帮助我们准确地计算出窗帘轨道在转角处的弧度值，为窗帘的安装和使用提供重要的参考数据。