计量值控制图系数表
- 格式:doc
- 大小:78.50 KB
- 文档页数:1

“六西格玛管理” 课程考试试题一、叙述题(40分,每小题5分)1.六西格玛的定义;答:六西格玛是一套系统的业务改进方法体系,是旨在持续改进企业业务流程,实现客户满意的管理方法。
它通过系统地、集成地采用业务改进流程,实现无缺陷的过程设计,并对现有过程进行过程定义(Define)、测量(Measure)、分析(Analyze)、改进(Improve)、控制(Control),简称DMAIC流程,消除过程缺陷和无价值作业,从而提高质量和服务、降低成本、缩短运转周期,达到客户完全满意,增强企业竞争力。
2.六西格玛质量水平的缺陷率是多少?如何解释该缺陷率;答;六西格玛在统计上表示一个流程或产品在一百万次使用机会中只出现3.4个缺陷。
3.亲和图的作用;答:亲和图的主要用途有:①认识事物,对未知的事物或领域,认真收集实际资料。
并从杂乱无章的资料中整理出事物的相互关系和脉络,就某件事情达成共识;②打破常规,打破旧框框,创造新思想,用亲和图法,重新确立自己的思想,提出新的方针;③归纳思想,由相互理解的人员组成计划小组,为着共同的目标,小组成员提出自己的经验、意见和想法,然后将这些资料编成卡片并利用亲和图解法进行整理;④贯彻方针。
亲和图可以帮助人们举行讲座,充分讨论,集思广益,从而将方针自然地贯彻下去。
4.过程决策程序图的作用;答:过程决策程序图法(PDPC法)针对要达成目标的计划,尽量导向预期理想状态的一种手段。
要求在制定计划或系统设计时,事先预测可能发生的障碍(不理想事态或结果),从而设计出一系列对策措施以最大的可能引向最终目标(达到理想结果)。
该法可用于防止重大事故的发生,因此也称之为重大事故预测图法。
5.直方图与排列图的作用;答:直方图的作用如下:(1)检验数据分布的类型,分析数据是否服从正态分布,判断数据有无异常;(2)与产品规格界限做比较,可直观地判断分布中心是否偏离规格中心,以确定是否需要调整并求出其调整量;还可判断数据分布的散差(分布范围)是否满足规格范围的要求,以确定是否采取缩小散差的技术性措施;(3)用于进行过程能力调查和不合格品率估计;(4)客观地反映操作者的技术水平和主观努力程度。





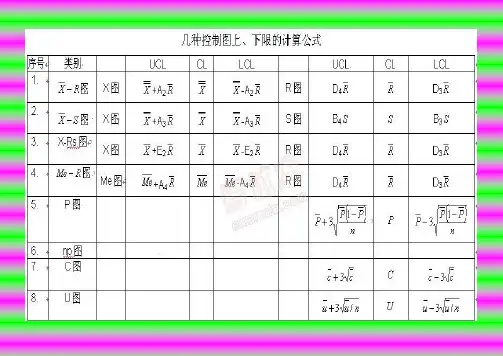
计量 值 控 制 图均值极差图图R X -X CL =R CL =中位数极差图 图R X -~X CL ~=R CL =单值移动极差控制图 图S R X - 计算简便效果差X CL =s R CL =S R UCL 267.3= LCL=不考虑平均值标准差图 图S X -X CL =S A X UCL 3+=S A X UCL 3-=S CL =S B UCL 4=S B UCL 3= 计 数 值 控 制 图不合格品数控制图Pn(Np) 样本数量相等n P CL =不合格品率控制图P样本数量可以不等计算量大,控制线凹凸不平(在特定条件下,控制线可为直线)P CL =缺陷数控制图C样本数量相等C CL = C C UCL 3+= C C UCL 3-=单位缺陷数控制图 U样本数量可以不等计算量大,控制线凹凸不平(在特定条件下,控制线可为直线) U CL = niU U UCL 3+= niU U UCL 3-= 标准差标准差(Standard Deviation) 也称均方差(mean square error)各数据偏离平均数的距离(离均差)的平均数,它是离差平方和平均后的方根。
用σ表()i P n p p P UCL -+=13RA X UCL X 2+=R A XLCL X 2-=RD R UCL 4=R D R LCL 3=R D R UCL 4=R D R LCL 3=RA X UCL m X 23~+=RA X UCL m X 23~-=S R X UCL 660.2+=S R X UCL 660.2-=()iP n pp Pn UCL -+=13()i P n pp Pn UCL --=13()iP n pp P UCL --=13=∑=--=ni i n X X S 121)(ˆσ在讨论控制图原理时,已经知道点子出界就判断异常,这是判断异常的最基本的一条准则。
为了增加控制图使用者的信心,即使对于在控制界限内的点子也要观察其排列是否随机。

均数-极差控制图(R x -图) 1、 均数控制部分中心线——nx x n x x i ∑∑⎪⎭⎫ ⎝⎛+==2上下控制线——R A x 2±上线警告线——R A x 232± 上线辅助线——R A x 231±2、 极差控制部分上控制线——R D 4上警告线——()R R D R -+432上辅助线——()R R D R -+431下控制线 ——R D 3方法与均数同,但是数据超出两表中任一则视为“失控”均数控制图绘制方法及使用方法:总均值()i x 、标准偏差()s 、平均差()R 等。
其中:2'i i i x x x +=nxx ii ∑=()122--=∑∑n nx x s ii'ii i x x R -= nR R i∑=以测定过程为横坐标,相应的测定值为纵坐标作图。
同时作有关控制线。
中心线(CL )——以总均数值来绘制,即i x 上下控制线(UCL,LCL )——按s x i 3±来绘制。
上下警告线(UWL,LWL )——按s x i 2±来绘制 上下辅助线(UAL,LAL )——按s x i ±来绘制在绘制图时,落在s x i ±范围内的点数应约占总点数的68%。
若少于50%,则分布不合适,说明所绘制的图不可靠。
若连续7点位于中心线同一侧,表示数据失控。
——————————————————————————————相某人汇编于2008年4月17日星期四。

