2021版新高考数学一轮复习讲义：第一章第三讲 逻辑联结词、全称量词与存在量词 (含解析)

2021年高考数学大一轮复习第一章第3课简单的逻辑联结词、全称量词与存在量词自主学习1. 全称量词我们把表示全体的量词称为全称量词.对应日常语言中的“一切”、“任意的”、“所有的”、“凡是”、“任给”、“对每一个”等词,用符号“”表示.含有全称量词的命题,叫作全称命题.“对任意实数x∈M,都有p(x)成立”简记成“x∈M,p(x)”.2. 存在量词我们把表示部分的量词称为存在量词.对应日常语言中的“存在一个”、“至少有一个”、“有个”、“某个”、“有些”、“有的”等词,用符号“”表示.含有存在量词的命题,叫作存在性命题.“存在实数x0∈M,使p(x)成立”简记成“x0∈M,p(x)”.3. 简单逻辑联结词有或(符号为∨),且(符号为∧),非(符号为¬).4. 命题的否定:“x∈M,p(x)”与“x0∈M,¬p(x)”互为否定.5. 复合命题的真假:对p且q而言,当p,q均为真时,其为真;当p,q中至少有一个为假时,其为假.对p或q而言,当p,q均为假时,其为假;当p,q中有一个为真时,其为真;当p为真时,¬p为假;当p为假时, ¬p为真.6. 常见词语的否定如下表所示:词语是一定是都是大于小于词语的否定不是不一定是不都是小于或等于大于或等于词语且必有一个至少有n个至多有一个所有x成立词语的否定或一个也没有至多有n-1个至少有两个存在一个x不成立1. (选修1-1P15例1(4)改编)若命题p:x∈R,x2+x+1=0,则¬p 为.[答案]x∈R,x2+x+1≠02. (选修1-1P17习题2(1)改编)“x∈R,2x2-3x+4>0”的否定为.[答案]x∈R,2x2-3x+4≤03. (选修1-1P17习题2(4)改编)命题“对于函数f(x)=x2+(a∈R),对任意的a∈R,使得f(x)是偶函数”是命题.(填“真”或“假”)[答案]假4. (选修1-1P17习题2(4)改编)命题“对于函数f(x)=x2+(a∈R),存在a∈R,使得f(x)是偶函数”是命题.(填“真”或“假”)[答案]真[解析]当a=0时,函数f(x)是偶函数.5. (选修1-1P20习题3改编)已知命题p“x∈R,sinx+cosx>m”是真命题,那么实数m的取值范围是.[答案](-∞,-)[解析]x∈R,sinx+cosx=sin∈[-,],所以m<-.35302 89E6 触137981 945D 鑝35025 88D1 裑26372 6704 朄29497 7339 猹36726 8F76 轶=/21630 547E 呾35471 8A8F 誏-23862 5D36 崶L。

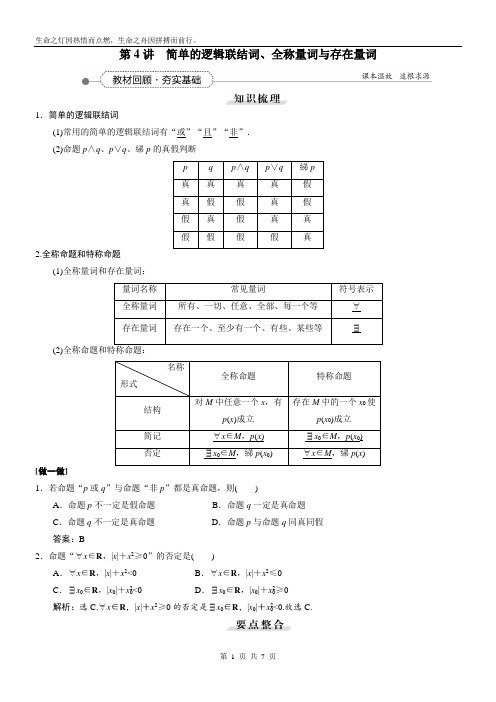
第4讲简单的逻辑联结词、全称量词与存在量词1．简单的逻辑联结词(1)常用的简单的逻辑联结词有“或”“且”“非”．(2)命题p∧q、p∨q、綈p的真假判断p q p∧q p∨q 綈p真真真真假真假假真假假真假真真假假假假真2.全称命题和特称命题(1)全称量词和存在量词：量词名称常见量词符号表示全称量词所有、一切、任意、全部、每一个等∀存在量词存在一个、至少有一个、有些、某些等∃(2)名称形式全称命题特称命题结构对M中任意一个x，有p(x)成立存在M中的一个x0使p(x0)成立简记∀x∈M，p(x)∃x0∈M，p(x0)否定∃x0∈M，綈p(x0)∀x∈M，綈p(x) [做一做]1．若命题“p或q”与命题“非p”都是真命题，则()A．命题p不一定是假命题B．命题q一定是真命题C．命题q不一定是真命题D．命题p与命题q同真同假答案：B2．命题“∀x∈R，|x|＋x2≥0”的否定是()A．∀x∈R，|x|＋x2<0B．∀x∈R，|x|＋x2≤0C．∃x0∈R，|x0|＋x20<0 D．∃x0∈R，|x0|＋x20≥0解析：选C.∀x∈R，|x|＋x2≥0的否定是∃x0∈R，|x0|＋x20<0.故选C.1．注意两类特殊命题的否定(1)注意命题是全称命题还是特称命题，是正确写出命题的否定的前提．(2)注意命题所含的量词，对于量词隐含的命题要结合命题的含义显现量词，再进行否定．2．含逻辑联结词命题真假的判断方法(1)p∧q中一假即假．(2)p∨q中一真必真．(3)綈p真，p假；綈p假，p真．[做一做]3．命题p：∀x∈R，sin x＜1；命题q：∃x∈R，cos x≤－1，则下列结论是真命题的是() A．p∧q B．綈p∧q C．p∨綈q D．綈p∧綈q解析：选B.p是假命题，q是真命题，所以B正确．4．p：菱形的对角线互相垂直；则綈p：______________．答案：有的菱形的对角线不垂直考点一：全称命题、特称命题(高频考点)全称命题与特称命题是高考的常考内容，多和其他数学知识相结合命题，常以选择题、填空题的形式出现．高考对全称命题、特称命题的考查主要有以下两个命题角度：(1)判断全称命题、特称命题的真假性；(2)全称命题、特称命题的否定．(1)已知命题p：∀x>0，总有(x＋1)e x>1，则綈p为()A．∃x0≤0，使得(x0＋1)e x0≤1 B．∃x0>0，使得(x0＋1)e x0≤1C．∀x>0，总有(x＋1)e x≤1 D．∀x≤0，总有(x＋1)e x≤1(2)已知函数f(x)＝x2＋bx(b∈R)，则下列结论正确的是()A．∀b∈R，f(x)在(0，＋∞)上是增函数B．∀b∈R，f(x)在(0，＋∞)上是减函数C．∃b∈R，f(x)为奇函数D．∃b∈R，f(x)为偶函数(3)命题：“对任意k>0，方程x2＋x－k＝0有实根”的否定是________．[解析](1)“∀x>0，总有(x＋1)e x>1”的否定是“∃x0>0，使得(x0＋1)e x0≤1”．故选B.(2)注意到b＝0时，f(x)＝x2是偶函数．(3)全称命题的否定是特称命题，故原命题的否定是“存在k>0，方程x2＋x－k＝0无实根”．[答案](1)B(2)D(3)存在k>0，方程x2＋x－k＝0无实根[规律方法](1)判断全称命题真假时，要注意假命题时只需举出一个反例否定即可，而真命题必须保证对限定的集合中每一个元素都成立．(2)写含有一个量词的命题的否定，首先要明确这个命题是全称命题还是特称命题，并找到其量词的位置及相应结论，然后把命题中的全称量词改成存在量词，存在量词改成全称量词，同时否定结论．1.(1)下列命题中，真命题是()A．∀x∈R，x2>0 B．∀x∈R，－1<sin x<1C．∃x0∈R，2x0<0 D．∃x0∈R，tan x0＝2(2)命题“函数y＝f(x)(x∈M)是偶函数”的否定可表示为()A．∃x0∈M，f(－x0)≠f(x0) B．∀x∈M，f(－x)≠f(x)C．∀x∈M，f(－x)＝f(x) D．∃x0∈M，f(－x0)＝f(x0)(3)若命题“∃x0∈R，2x20－3ax0＋9<0”为假命题，则实数a的取值范围是________．解析：(1)∀x∈R，x2≥0，故A错．∀x∈R，－1≤sin x≤1，故B错．由y＝2x的图象可知∀x∈R，2x>0，故C错．D正确．(2)由偶函数的定义及命题“函数y＝f(x)(x∈M)是偶函数”，可知“∀x∈M，f(－x)＝f(x)”，该命题是一个全称命题，其否定是一个特称命题，即“∃x0∈M，f(－x0)≠f(x0)”．(3)因为“∃x0∈R，2x20－3ax0＋9<0”为假命题，则“∀x∈R，2x2－3ax＋9≥0”为真命题．因此Δ＝9a2－4×2×9≤0，故－22≤a≤2 2.答案：(1)D(2)A(3)[－22，22]考点二：含有逻辑联结词的命题的真假判断已知命题p：对任意x∈R，总有2x>0；q：“x>1”是“x>2”的充分不必要条件．则下列命题为真命题的是()A．p∧q B．綈p∧綈q C．綈p∧q D．p∧綈q[解析]因为指数函数的值域为(0，＋∞)，所以对任意x∈R，y＝2x>0恒成立，故p为真命题；因为当x>1时，x>2不一定成立，反之当x>2时，一定有x>1成立，故“x>1”是“x>2”的必要不充分条件，故q为假命题，则p∧q、綈p为假命题，綈q为真命题，綈p∧綈q、綈p∧q为假命题，p∧綈q为真命题，故选D.[答案] D[规律方法]若要判断一个含有逻辑联结词的命题即复合命题的真假，其步骤如下：(1)判断复合命题的结构；(2)判断构成这个命题的每个简单命题的真假；(3)依据“或”——一真即真，“且”——一假即假，“非”——真假相反，作出判断即可．2.已知命题p1：∃x0∈R，x20＋x0＋1<0；p2：∀x∈[1，2]，x2－1≥0.以下命题为真命题的是()A．綈p1∧綈p2B．p1∨綈p2 C．綈p1∧p2D．p1∧p2解析：选C.对于命题p1，因为Δ＝1－4<0，所以p1是假命题，p2：∀x∈[1，2]，x2－1≥0是真命题，故綈p1∧p2为真命题．考点三：由命题真假确定参数的取值范围已知p：∃x∈R，mx2＋1≤0，q：∀x∈R，x2＋mx＋1＞0，若p∨q为假命题，则实数m的取值范围为()A ．m ≥2B ．m ≤－2C ．m ≤－2或m ≥2D ．－2≤m ≤2 [解析] 依题意知p ，q 均为假命题，当p 是假命题时，mx 2＋1＞0恒成立，则有m ≥0； 当q 是真命题时，则有Δ＝m 2－4＜0，－2＜m ＜2. 因此由p ，q 均为假命题得⎩⎪⎨⎪⎧m ≥0m ≤－2或m ≥2，即m ≥2. [答案] A若本例中的条件“p ∨q 为假命题”变为“p ∧(綈q )为真命题”，其他条件不变，求实数m 的取值范围．解：由p ∧(綈q )知p 为真命题且q 为假命题．p 为真命题，则m <0，q 为假命题，∴Δ≥0，则m ≥2或m ≤－2.∴m ≤－2， 实数m 的取值范围为(－∞，－2]． [规律方法] 根据命题真假求参数的方法步骤：(1)先根据题目条件，推出每一个命题的真假(有时不一定只有一种情况)； (2)然后再求出每个命题是真命题时参数的取值范围； (3)最后根据每个命题的真假情况，求出参数的取值范围．3.已知命题p ：存在实数x ，使得不等式x 2＋2ax ＋a ≤0成立．若命题p 是假命题，求实数a 的取值范围．解：法一：当命题p 是真命题时，有(x 2＋2ax ＋a )min ≤0，即a －a 2≤0，得a ≥1或a ≤0，故当命题p 是假命题时，有0<a <1.法二：若命题p 是假命题，则不存在实数x ，使得不等式x 2＋2ax ＋a ≤0成立，即对于任意的实数x ，不等式x 2＋2ax ＋a >0恒成立，从而Δ＝4a 2－4a <0，得0<a <1.方法思想——分类讨论思想求解命题中的参数已知c >0，且c ≠1，设p ：函数y ＝c x 在R 上单调递减；q ：函数f (x )＝x 2－2cx ＋1在⎝⎛⎭⎫12，＋∞上为增函数，若“p 且q ”为假，“p 或q ”为真，求实数c 的取值范围．[解] ∵函数y ＝c x 在R 上单调递减，∴0<c <1，即p ：0<c <1. ∵c >0且c ≠1，∴綈p ：c >1.又∵f (x )＝x 2－2cx ＋1在⎝⎛⎭⎫12，＋∞上为增函数，∴c ≤12，即q ：0<c ≤12.∵c >0且c ≠1，∴綈q ：c >12且c ≠1.又∵“p 或q ”为真，“p 且q ”为假，∴p 真q 假或p 假q 真． ①当p 真，q 假时，{c |0<c <1}∩{c |c >12，且c ≠1}＝{c |12<c <1}．②当p 假，q 真时，{c |c >1}∩{c |0<c ≤12}＝∅.综上所述，实数c 的取值范围是{c |12<c <1}．[名师点评] 解答本题时运用了分类讨论思想，由条件可知p 、q 一真一假，因此需分p 真q 假与p 假q 真两类讨论，分别求解，最后将解合并，实质上，分类讨论是“化整为零，各个击破，再积零为整”的解题策略．已知两个命题r ：sin x ＋cos x >m ；s ：x 2＋mx ＋1>0.如果对任意的x ∈R ，r 与s 有且仅有一个是真命题，求实数m 的取值范围．解：∵sin x ＋cos x ＝2sin ⎝⎛⎭⎫x ＋π4≥－2，∴当r 是真命题时，m <－ 2.又∵对任意的x ∈R ，s 为真命题，即x 2＋mx ＋1>0恒成立， ∴Δ＝m 2－4<0∴－2<m <2. 当r 为真，s 为假时，需满足m <－2，且m ≤－2或m ≥2，∴m ≤－2； 当r 为假，s 为真时，需满足m ≥－2且－2<m <2，∴－2≤m <2.综上所述，实数m 的取值范围是{m |m ≤－2或－2≤m <2}．1．命题“存在一个无理数，它的平方是有理数”的否定是( )A ．任意一个有理数，它的平方是有理数B ．任意一个无理数，它的平方不是有理数C ．存在一个有理数，它的平方是有理数D ．存在一个无理数，它的平方不是有理数解析：选B.根据特称命题的否定是全称命题可知，原命题的否定为“任意一个无理数，它的平方不是有理数”．2．已知f (x )＝3sin x －πx ，命题p ：∀x ∈⎝⎛⎭⎫0，π2，f (x )<0，则( )A ．p 是假命题，綈p ：∀x ∈⎝⎛⎭⎫0，π2，f (x )≥0B ．p 是假命题，綈p ：∃x 0∈⎝⎛⎭⎫0，π2，f (x 0)≥0C ．p 是真命题，綈p ：∀x ∈⎝⎛⎭⎫0，π2，f (x )>0D ．p 是真命题，綈p ：∃x 0∈⎝⎛⎭⎫0，π2，f (x 0)≥0解析：选D.因为f ′(x )＝3cos x －π，所以当x ∈⎝⎛⎭⎫0，π2时，f ′(x )<0，函数f (x )单调递减，所以∀x ∈⎝⎛⎭⎫0，π2，f (x )<f (0)＝0，所以p 是真命题，又全称命题的否定是特称命题，所以答案选D.3．设a ，b ，c 是非零向量．已知命题p ：若a ·b ＝0，b ·c ＝0，则a ·c ＝0；命题q ：若a ∥b ，b ∥c ，则a ∥c .则下列命题中真命题是( )A ．p ∨qB ．p ∧qC ．(綈p )∧(綈q )D ．p ∨(綈q ) 解析：选A.由题意知命题p 为假命题，命题q 为真命题，所以p ∨q 为真命题．故选A. 4．若命题“∃x 0∈R ，x 20＋(a －1)x 0＋1<0”是真命题，则实数a 的取值范围是( )A ．[－1，3]B ．(－1，3)C ．(－∞，－1]∪[3，＋∞)D ．(－∞，－1)∪(3，＋∞)解析：选D.因为命题“∃x 0∈R ，x 20＋(a －1)x 0＋1<0”等价于x 20＋(a －1)x 0＋1＝0有两个不等的实根，所以Δ＝(a －1)2－4>0，即a 2－2a －3>0，解得a <－1或a >3，故选D.5．已知命题p ：∃x 0∈R ，e x 0－mx 0＝0，q ：∀x ∈R ，x 2＋mx ＋1≥0，若p ∨(綈q )为假命题，则实数m 的取值范围是( )A ．(－∞，0)∪(2，＋∞)B ．[0，2]C ．RD ．∅解析：选B.若p ∨(綈q )为假命题，则p 假q 真．命题p 为假命题，有0≤m <e ；命题q 为真命题时， 有Δ＝m 2－4≤0，即－2≤m ≤2.最后要使p ∨(綈q )为假命题，m 的取值范围是0≤m ≤2. 6．命题p 的否定是“对所有正数x ，x >x ＋1”，则命题p 是________．解析：因为p 是綈p 的否定，所以只需将全称命题变为特称命题，再对结论否定即可． 答案：∃x 0∈(0，＋∞)，x 0≤x 0＋17．若命题p ：关于x 的不等式ax ＋b >0的解集是{x |x >－ba }，命题q ：关于x 的不等式(x －a )(x －b )<0的解集是{x |a <x <b }，则在命题“p ∧q ”、“p ∨q ”、“綈p ”、“綈q ”中，是真命题的有________．解析：依题意可知命题p 和q 都是假命题，所以“p ∧q ”为假、“p ∨q ”为假、“綈p ”为真，“綈q ”为真． 答案：綈p ，綈q8．已知命题p ：函数y ＝(c －1)x ＋1在R 上单调递增；命题q ：不等式x 2－x ＋c ≤0的解集是∅.若p 且q 为真命题，则实数c 的取值范围是________．解析：若命题p 是真命题，则c －1>0，c >1；若命题q 是真命题，则Δ＝1－4c <0，c >14.因此，由p 且q 是真命题得⎩⎪⎨⎪⎧c >1，c >14，即c >1，即实数c 的取值范围是(1，＋∞)．答案：(1，＋∞)9．命题p ：∀x ∈(1，＋∞)，函数f (x )＝|log 2x |的值域为[0，＋∞)；命题q ：∃m ≥0，使y ＝sin mx 的周期小于π2，试判断p ∨q ，p ∧q ，綈p 的真假性．解：对于命题p ，当f (x )＝|log 2x |＝0时，log 2x ＝0，即x ＝1，1∉(1，＋∞)，故命题p 为假命题．对于命题q ，y ＝sin mx 的周期T ＝2π|m |<π2，即|m |>4，故m <－4或m >4，故存在m ≥0，使得命题q 成立，故p ∨q 为真命题，p ∧q 为假命题，綈p 为真命题．10．已知命题p ：存在一个实数x ，使ax 2＋ax ＋1＜0.当a ∈A 时，非p 为真命题，求集合A .解：非p 为真，即“∀x ∈R ，ax 2＋ax ＋1≥0”为真． 若a ＝0，则1≥0成立，即a ＝0时非p 为真；若a ≠0，则非p 为真⇔⎩⎪⎨⎪⎧a ＞0Δ＝a 2－4a ≤0⇔0＜a ≤4. 综上知，所求集合A ＝[0，4]．。

2021年新高考数学总复习第一章《集合与常用逻辑用语》第3节全称量词与存在量词、
逻辑联结词“且”“或”“非”
考试要求 1.了解逻辑联结词“且”、“或”、“非”的含义；2.理解全称量词与
.
存在量词的意义；3.能正确地对含有一个量词的命题进行否定
1.简单的逻辑联结词
(1)命题中的且、或、非叫作逻辑联结词.
(2)命题p且q，p或q，非p的真假判断
p q p且q p或q 非p
真真真真假
真假假真假
假真假真真
假假假假真
2.
(1)常见的全称量词有：“任意一个”“一切”“每一个”“任给”“所有的”等.
(2)常见的存在量词有：“存在一个”“至少有一个”“有些”“有一个”“某个”“有的”等.
3.全称命题和特称命题
名称全称命题特称命题
结构对M中的任意一个x，有p(x)成立存在M中的一个x0，使p(x0)成立简记任意x∈M，p(x)存在x0∈M，p(x0)
否定存在x0∈M，非p(x0)任意x∈M，非p(x)
1.含有逻辑联结词的命题真假判断口诀：p或q→见真即真，p且q→见假即假，p
第1 页共16 页。

1．3 简单的逻辑联结词、全称量词与存在量词
[知识梳理]
1．简单的逻辑联结词
(1)命题中的或、且、非叫做逻辑联结词．
(2)概念
用联结词“且”把命题p和命题q联结起来，得到复合命题“p 且q”，记作p∧q；
用联结词“或”把命题p和命题q联结起来，得到复合命题“p 或q”，记作p∨q；
对命题p的结论进行否定，得到复合命题“非p”，记作綈p.
(3)命题p∧q，p∨q，綈p的真假判断
(4)命题的否定与否命题的区别
①定义：命题的否定是直接对命题的结论进行否定，而否命题则是对原命题的条件和结论分别否定，即命题“若p，则q”的否定为“若p，则綈q”，而否命题为“若綈p，则綈q”．
②与原命题的真假关系：命题的否定的真假与原命题的真假总是相对的，即一真一假，而否命题的真假与原命题的真假无必然的联系．2．全称量词和存在量词
3．全称命题和特称命题
4．复合命题的否定
(1)“綈p”的否定是“p”；
(2)“p∨q”的否定是“(綈p)∧(綈q)”；
(3)“p∧q”的否定是“(綈p)∨(綈q)”．
[诊断自测]
1．概念思辨
(1)若p∧q为真，则p∨q必为真；反之，若p∨q为真，则p∧q 必为真．()
(2)全称命题一定含有全称量词，特称命题一定含有存在量词．()
(3)写特称命题的否定时，存在量词变为全称量词．()
(4)∃x0∈M，p(x0)与∀x∈M，綈p(x)的真假性相反．()。