当前位置：文档之家 › 电通量、高斯定理

电通量、高斯定理

  • 格式：doc
  • 大小：178.00 KB
  • 文档页数：5

下载文档原格式

  / 5

合集下载

高斯定理

高斯定理
限远处），无电荷处不中断。
2.任何两条电场线不会相交。 3.电场线不能形成闭合曲线。
二.电通量
在电场中穿过任意曲面S 的电场线条数称为穿
过该面的电通量（
1. 均匀场中 dN
E dS
）e。
E
n
de EdS
dS
dS
定义 dSEddSsncos
de E dS
2. 非均匀场中
de E dS
求 均匀带电球体的电场强度分布
解 球外 (r R)
E
1
4 0
q r2
r0
30
R3 r2
r0
球内( r R )
r
++
R r' + +
E
dS
E
4r2
1 4 r3
1 q'
S
0 3
0
E r
E
3 0
O
r R 电场分布曲线
例3 已知“无限长”均匀带电直线的电荷线密度为+
求 距直线r 处一点P 的电场强度
q
+
r
=
e0
② 点电荷不在球心时
点电荷不在球心时，这一 结果仍是一样的，这由图 也可看出。
而且，电通量与所选取球 面半径无关，
③ q在曲面外时： +q
e e1 e2 0
S1
S2
S
④闭合面内为点电荷系的情况：
E E1 E2 En
e E dS (E1 E2 ... E5) dS
q3
q1
q2
E1 dS E2 dS ... E5 dS
q4
q5
q1 q2 q3
0 0 0

2.3.1-4电通量和高斯定理

2.3.1-4电通量和高斯定理
d e E dS EdS
4 0 R
S
ds q r
E
q dS 2 4 0 R
1
2.3 电通量和高斯定理
三、高斯定律
(二)证明 出发点：库仑定律和叠加原理 1.通过一个与点电荷q 同 心的球面S的电通量。
e d e
s
S
q
0
q 40 R
2.3 电通量和高斯定理
二、电场强度通量
(二)匀强电场的电通量
1.平面S与E垂直时
e＝ES
2.平面S与E有夹角θ时 引入面积矢量
e＝ES cos e＝E S E en S
S Se n
E

S
en
S
2.3 电通量和高斯定理
二、电场强度通量
例4、求一半径为R，单位长度带电 的无 限长直圆柱带电体的电场。 解：1、对称性分析：
E
+ + +++ +++ +++
+ + +
+ + + + +
+
+++ 结论：电场以中心轴线为对称轴。
例4、求一半径为R，单位长度带电 的无 限长直圆柱带电体的电场。 2、以轴线为中心， 作半径为r(r>R)的圆柱形 高斯面S
2.3 电通量和高斯定理
4.若高斯面内的电荷的电量为零，则通过 高斯面的电通量为零，但高斯面上各点的电场 强度并不一定为零； 5.通过任意闭合曲面的电通量只决定于它 所包围的电荷的代数和，闭合曲面外的电荷对 电通量无贡献。但电荷的空间分布会影响闭合 面上各点处的场强大小和方向； 6.高斯定理中所说的闭合曲面，通常称为 高斯面。

电通量,高斯定理

电通量,高斯定理

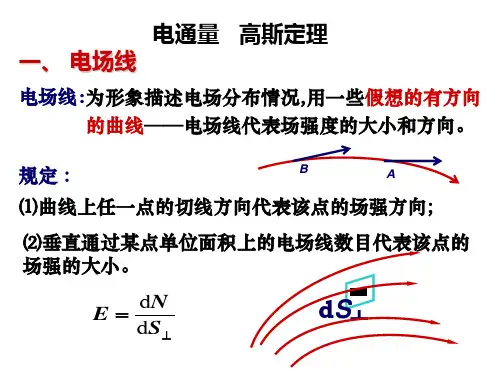
电通量、高斯定理1、均匀电场的场强E与半径为R 的半球面的轴线平行，则通过半球面的电场强度通量φ = πR 2E ，若在半球面的球心处再放置点电荷q ，q不改变E分布，则通过半球面的电场强度通量 φ =πR 2E ±q/2ε0。

2、真空中的高斯定理的数学表达式为∑⎰=⋅0/εq s d E i s ，其物理意义是静电场是有源场。

3、一点电荷q 位于一位立方体中心，立方体边长为a ，则通过立方体每个表面的E的通量是q/6ε0；若把这电荷移到立方体的一个顶角上，这时通过电荷所在顶角的三个面E的通量是 0 ，通过立方体另外三个面的E的通量是 q/8ε0。

4、两个无限大均匀带正电的平行平面，电荷面密度分别为σ1和σ2，且σ1＞σ2，则两平面间电场强度的大小是( C )(A)(B) (C)(D) 5、应用高斯定理求场强E时，要求E的分布具有对称性，对于没有对称性的电场分布，例如电偶极子产生的电场，高斯定理就不再成立，你认为这种说法：( B )(A)正确 (B)错误 (C)无法判断6、下述带电体系的场强分布可能用高斯定理来计算的是( D )(A)均匀带电圆板 (B)有限长均匀带电棒 (C)电偶极子 (D)带电介质球(电荷体密度是离球心距离r 的函数) 7、如果在静电场中所作的封闭曲面内没有净电荷，则( C )(A)封闭面上的电通量一定为零，场强也一定为零；()0212/εσσ+()021/εσσ+()0212/εσσ-()021/εσσ-(B)封闭面上的电通量不一定为零，场强则一定为零；(C)封闭面上的电通量一定为零；场强不一定为零；(D)封闭面上的电通量不一定为零；场强不一定为零。

8、无限长均匀带电圆柱体，电荷体密度为ρ，半径为R，求柱体内外的场强分布解：作一半径为r，高为h的同轴圆柱面为高斯面根据对称性分析，圆柱面侧面上任一点的场强大小相等，方向沿矢径方向⎰⎰⎰⎰⋅+⋅+⋅=⋅侧面下底上底s dEs dEs dEs dEs=⎰⋅侧面s dE=E⎰侧面ds=2rhEπ（1）r < R时, ∑=ρπhrqi2,2/2ερππhrrhE=,2ερrE=（2）r > R时, ∑=ρπhRqi2,2/2ερππhRrhE=,rRE22ερ=∴=E)(,2)(,22RrrRRrr><ερερ。

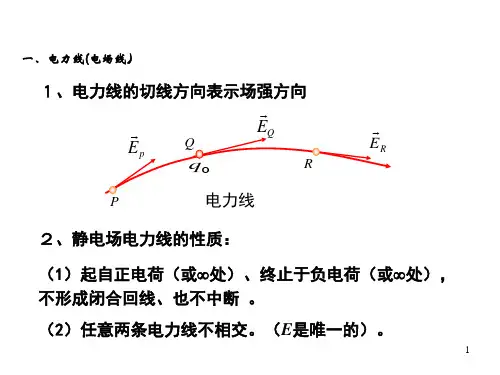
电通量高斯定理

电通量高斯定理
穿入曲面的电力线，电通量为负值； 与曲面相切或未穿过曲面的电力线，对通量无贡献。
5
三、高斯定理
1、真空中的高斯定理
穿过任一闭合曲面的电通量 等于该 曲面内所包围的所有电荷的代数和除以 ，而与闭合面外的电荷无关。
∑qi 是曲面S 内的电荷的代数和，这里的E是总电场(电 力线穿过曲面处的电场）、是S面内外所有电荷共同产生的 电场。
通过整个闭合球面S的电通量
e
d
s
e
qds
s 4 0r 2
q
4 0r 2
ds q
s
0
7
2）任意闭合曲面S／：
在该曲面外作一个以点电荷q 为中心的球面S
由于电力线的连续性、同前例
e
S
E
ds
q ε0
3）曲面S不包围q
n0
dS
S
从q发出的电力线
穿出任意闭合曲面
因为只有与S 相切的锥体内的电力线才通过S，但每一条 电力线一进一出闭合曲面、正负通量相互抵消，如下图。
10
3、正确理解高斯定理
1）高斯面上各点的场强E，例如P点的 EP 是所有在场的电荷
共同产生。高斯定理中的e只与高斯面内的电荷有关。
Ｅ
P
qB
qC
qD
＋
q
－
q
q A
2）高斯面内的电量为零，只能说明通过高斯面的e为零，但
不能说明高斯面上各点的E一定为零。
11
四、高斯定理的应用：
对于某些具有特殊对称性的带电体，利用高斯定理可以方 便地求出电场分布。 1、均匀带电球面的电场：(设总电量为q、球面的半径为R)
为对称。
19
设P为柱面外之一点，过

电通量 高斯定理

电通量 高斯定理
E1 ds E2 ds ...... En ds
qn q1 q2 0 0 0
e E ds
s 0
1 qi 0
q1 q2 qn
S
q E ds
s
0
E ds 0
q ds
S
n
S

s
q
2
40 r
q
2
ds
q
0

4 0 r
ds
q
2. q位于任意曲面
S 内
0
s s
3. q位于任意闭合曲面
4. 曲面内包围多个点电荷
S 以外
S
q

( E1 E2 ...... En ) ds
解： e E ds E ds E ds E ds
E cos180 ds E cos 90 ds E cos 0 ds
0 0 0 s1 s2 s3
ER 0 R E
2 2
=0
n
0
1 e E ds
s
0
qi
四．高斯定理的应用 当场源分布具有高度对称性时，求场强分布
步骤：１.对称性分析，确定 E 的大小、方向分布特征
２.作高斯面，计算电通量及 ３.利用高斯定理求解
qi
例1．球面 求均匀带电球面的场强分布 已知R、 q>0 解: 对称性分析 E 具有球对称 作高斯面 通量 r R
电量 q i
电量
qi q
q E 4r
2
高斯定理

大学物理电通量高斯定理

大学物理电通量高斯定理

高斯定理的应用范围
在静电场中，高斯定理广泛应用 于电荷分布和电场关系的分析。
在恒定磁场中，高斯定理可以用 来分析磁通量与电流之间的关系
。
高斯定理是解决物理问题的重要 工具之一，尤其在计算电场分布 、求解电势、分析带电体的相互
作用等方面具有广泛应用。
02
电通量和高斯定理的关系来自 电通量的定义和性质总结词
大学物理电通量高斯定理
汇报人： 202X-01-04
contents
目录
• 高斯定理的概述 • 电通量和高斯定理的关系 • 高斯定理的证明 • 高斯定理的应用实例
01
高斯定理的概述
高斯定理的内容
总结了电荷分布与电场之间的关系， 指出在空间中任一封闭曲面内的电荷 量与该封闭曲面上的电场通量之间存 在正比关系。
利用电场线证明高斯定理
总结词：直观明了
详细描述：通过电场线的闭合曲线围成的面积的电通量与该闭合曲线所包围的电荷量的关系，证明高 斯定理。
利用高斯公式证明高斯定理
总结词：数学严谨
详细描述：利用高斯公式，将空间分成无数小的体积元，再通过求和得到整个空间的电场分布，从而证明高斯定理。
利用微积分证明高斯定理
详细描述
高斯定理是描述电通量与电荷分布关系的定理，它指出在任意闭合曲面内的电荷量等于该闭合曲面所包围的体积 内电场线的总条数。这个定理表明，电荷分布与电场线数之间存在一定的关系，即电荷分布影响电场线的分布。
电通量和高斯定理的推导过程
总结词
通过数学推导，我们可以证明高斯定理的正确性。首先，我们定义电场线密度为电场强 度与垂直于曲面的面积之比，然后利用微积分原理和格林公式，推导出高斯定理的表达
公式表达为：∮E·dS = 4πkQ，其中 ∮E·dS表示封闭曲面上的电场通量，Q 表示曲面内的电荷量。

2电通量 高斯定理

2电通量 高斯定理
S
Φ 0
out ei
E
1 in in Φe i qi ε0 1 n in E dS qi ε0 i 1 S
dS
s
qi
14
物理学
第五版
◆ 高斯定理
高斯面
真空静电场中，穿过任一闭合曲面的电通量，等于该 曲面所包围的所有电荷的代数和除以 ε 。
0
1 n in Φe E cos dS qi ε0 i 1 S

v E
dN EdS E cos dS
◆ 面元的电通量
dΦ E cos dS
实质：通过面的电场线根数。 是一个标量，正负取决于夹角。 7
物理学
第五版
◆ 匀强电场中通过平面的电通量
Φe ES cos
◆ 非匀强电场中通过曲面的电通量
s

s

r en
v E
v E
r en
Φe E cos dS
E E1 E2
3
（补偿法）
d
P
O
d

O
对于 P点：

a
d E1 方向:水平向左 3 0 a3 E2 方向:水平向左 3 0 (2d )2 3 d a EP 方向:水平向左 2 3 0 3 0 (2d )
R
20
物理学
第五版
[例] 求无限长均匀带电直线的电场强度。
第五版
◆ 点电荷在闭合曲面S外
dΦ1 E1 dS1 0 dΦ2 E2 dS2 0
dS1
q
+
dΦ1 dΦ2 0
E2
E1

104电通量高斯定理

104电通量高斯定理
24
金属导电模型
构成导体旳框架、 形状、 大小旳是那些 基本不动旳带正电荷旳原子核, 而自由电子充 斥整个导体, 属于导体共有。当有外电场存在 时, 电场与导体旳相互作用使得导体内旳自由 电子重新分布, 从而决定了导体旳电学性质。
自由电子
导体带电-q
q
25
一、 导体旳静电平衡
将导体放入电场强度为 附E0加旳电外场电场E时。, 其内部产生
E 2 0r
r
l n E n
22
总结 静电场旳高斯定理合用于一切静电场；
高斯定理并不能求出全部静电场旳分布。
高斯定理求解电场分布
E
dS
1
0
q内
场强 E 能否提出积分号
带电体电荷分 建立旳高斯 布旳对称性 面是否合适
23
10.7 静电场中旳导体
前面讨论了真空中旳静电场, 实际旳 电场中往往存在多种导体或实物介质, 这 些宏观物体旳存在会与电场产生相互作用 和相互影响, 从而出现某些新旳现象。 下 面将讨论导体在静电场中旳性质和行为。
二、电场强度通量 Φe
穿过任意曲面
旳电场线条数称为
电通量。
S
4
1.均匀场中dS 面元旳电通量
n
de dN EdS
E cos dS
E
矢量面元
dS
dS
n
dS
de E dS
2.非均匀场中曲面旳电通量
dS
S
dS E
e de SE dS
5
3. 闭合曲面电通量
E
e de SE dS
E
dS
r
11
2. 多种 电荷
E E1 E2 ... E5
q5 q3 q2

高二物理竞赛课件：电通量高斯定理

高二物理竞赛课件：电通量高斯定理

3.静电场电场线的性质 1)电场线起始于正电荷(或无穷远处)， 终止于负电荷，不会在没有电荷处中断； 2)两条电场线不会相交； 3)电场线不会形成闭合曲线。
由静电场的基本性质和场的单值性决定的。 可用静电场的基本性质方程加以证明。
[思考] ①通过蓝红闭合曲面电力线数目相等吗? ②左右红闭合曲面电力线数目有区别吗?
i
②改为均匀带电的半圆环，线电荷密度
为0，结果？
Y
O
X
[例] 均匀带电(Q)直线段延长线上一点的场强．
L O x x+dx
a X
p
解：建立坐标轴如图
xx+dx电荷元在P点产生的场强：dE源自dq4 0r2
i
Q L
4 0(L
dx a
x)2
i
P点的总场强：
E dE i
Q
L
dx
4 0L 0 (L a x)2
电通量高斯定理
电通量 高斯定理
一、电场线 electric field line
E
1. 电场线：用一族空间曲线形象
a
描述场强分布
a
规定：
Eb
E
bc
c Ed
d
⑴ 曲线上每一点的切线方向表示该点电场强度E方向
⑵ 曲线的疏密表示该点处场强E的大小。某点的场强
大小等于该处的电场线密度，即：垂直通过单位面积
的电场线条数，在数值上就等于该点处电场强度的 大
小。
dS
E
dN E dS
－电场线密度 线密处场强大；线疏处场强小。
[例] 如图，带电圆环半径为 R，电荷线密度为 =0cos (0为一常量).求环心O点处的电场强度.
解： 由的分布规律知， E Exi

电通量高斯定理

电通量高斯定理
该定理是静电场的基本定理之，对 于研究静电场的分布和性质具有重要 意义。
03 电通量高斯定理的应用场 景
静电场计算
静电场计算是电通量高斯定理的重要 应用场景之一。通过使用高斯定理， 可以方便地计算出给定区域内电荷产 生的电场强度和电势分布。
在实际应用中，静电场计算广泛应用 于电子设备、电磁兼容性分析、材料 科学等领域。
内的电荷分布仍然满足高斯定理。这一理论为分析复杂电场问题提供了重要的基础。
电通量高斯定理与麦克斯韦方程组的关系
要点一
总结词
要点二
详细描述
电通量高斯定理是麦克斯韦方程组的一个推论，表明在时 变电磁场中，电场线闭合的特性与电荷守恒定律相一致。
麦克斯韦方程组是描述电磁场运动的基本方程，其中包括 了波动方程、高斯定理和安培环路定律等。在高斯定理中 ，它指出在时变电磁场中，电场线闭合的特性与电荷守恒 定律相一致。这意味着在变化的电磁场中，电荷分布的变 化必须满足电荷守恒定律，从而保持电场线的闭合性。这 一关系表明了电通量高斯定理与麦克斯韦方程组之间的紧 密联系。
推动科学发展
电通量高斯定理的发现和应用，推动了科学技术的进步和发展。在电子工程、通信工程、生物医学工程 等领域，电通量高斯定理都发挥了重要的作用，为各种先进技术和设备的研发提供了重要的理论支持。
对未来研究的展望
要点一
深入研究电磁场的内 在机制
随着科学技术的发展，对电磁场的内 在机制和规律的认识越来越深入。未 来可以进一步深入研究电通量高斯定 理的内在机制和规律，探索更加复杂 和深入的电磁场问题。
02 电通量高斯定理的公式与 推导
公式表述
公式
$oiint_{S} vec{E} cdot dvec{S} = frac{1}{varepsilon_{0}} iint_{S} rho dS$

电场的电通量与高斯定理

电场的电通量与高斯定理

电场的电通量与高斯定理电场的电通量是描述电场线通过一个封闭曲面的程度的物理量，它在物理学中有着重要的应用。

而高斯定理则是计算电场电通量的一种重要方法。

本文将探讨电场的电通量的概念及计算方法，以及高斯定理的原理和应用。

1. 电场的电通量电场的电通量是指单位时间内通过垂直于电场线的面积的电场线数目。

常用符号表示为Φ，单位为“麦可伏伦/米平方”（C·V/m^2）。

电通量的大小与电场线的密度有关，电场线越密集，则电通量越大。

2. 电通量的计算电通量的计算可以通过积分来实现。

设曲面S为一个封闭曲面，并在曲面上选取微小面元dS，该微小面元的面积为ΔS。

假设电场E在该面元上的投影长度为E⊥，则通过该微小面元的电场线条数为E⊥·ΔS。

将所有微小面元上的电场线条数相加，就可以得到通过整个曲面的电通量Φ，即Φ = ∫ E⊥ · dS。

3. 高斯定理的原理高斯定理主要应用于具有对称性的电场问题。

它指出，对于任意封闭曲面S，通过该曲面的电通量Φ与该封闭曲面所包围的总电荷量Q之间存在以下关系：Φ = Q/ε0，其中ε0为真空中的电介质常数，约等于8.85 × 10^-12 C^2/N·m^2。

4. 高斯定理的应用高斯定理在电场问题的求解中具有广泛的应用。

通过选择合适的封闭曲面，可以简化电场问题的求解过程。

例如，当电场具有球对称性时，可以选择以球心为中心的球面作为封闭曲面，这样可以使计算过程更加简化。

5. 实例分析考虑一个均匀带电球体，球心位于原点，半径为R，总电荷量为Q。

我们希望计算通过球面的电通量。

根据高斯定理，可以选择以球心为中心，球面为封闭曲面进行计算。

由于球对称性，电场E在球面上的大小处处相等。

根据球面积分的计算公式，可以得到Φ = E · 4πR^2。

而球内的总电荷量为Q，因此根据高斯定理，我们可以得到Φ = Q/ε0。

将上述两个等式联立，可以解得E = Q / (4πε0R^2)。

电通量 高斯定理

电通量 高斯定理

(2)选过场点和板对称且垂直的封闭柱面为高斯面 S3 S3 S1 S2 S1 + + + + + +

+ + S2
S 2 ( 3) e E dS 2 ES2
S
0
E 2 0
0 场强垂直于板向外 0 场强垂直于板向内
例5 两块均匀无限大薄平板相互垂直，它们的电荷 面密度为+σ和-σ。求空间各点的场强大小和方向， 并画出电力线。 解：由图，对空间任一 点，由场强叠加原理得
本节作业： P321 15 17 18 19 20
在空腔内任取一点p, 设该点场强为 E
Ε1 op 3 0
1
c o
E1
小球单独存在时，p点的场强为
E2 cp 3 0
ห้องสมุดไป่ตู้
o p E
R
2
E1 E 2 E ( op cp ) E E1 E2
3 0
l
侧面
+++ S下 +++
ES侧
q E 2πrl
E
q
2 π 0 rl
0
E
+ + +++ +++
q
2 π 0 rl
2
l
+++ +++
r > R： q π2R l R E 2 0 r 2 q π r l r R： r E E 2 0
令
Q Aa 0 2 2 4 0 r 2 0 r

1.2电通量 高斯定理

1.2电通量 高斯定理
而
+
+
r
+ + R

Q 4 3 R 3
q E 2 40 r
E
得
即
Qr E 3 40 R Qr E e 3 r 40 R
O
R 电场分布曲线
r
35
2
dS
+
Φe E dS
q 4π 0r
dS
Φe
q
0
15
大学 物理
1.2 电通量 高斯定理
点电荷在任意封闭曲面内
q 发出的 q / 0
条电场线仍全部穿出封闭
曲面 S ，即：
+
Φe
q
0
点电荷位于球面中心
Φe
q
0
16
大学 物理
1.2 电通量 高斯定理
1.2 电通量 高斯定理
高斯 (C.F.Gauss 17771855） 德国数学家、天文学 家和物理学家，有“数 学王子”美称，他与韦 伯制成了第一台有线电 报机和建立了地磁观测 台，高斯还创立了电磁 量的绝对单位制.
高
斯
大学 物理
1.2 电通量 高斯定理
三
高斯定理
在真空中,通过任一闭合曲面的电场强度通量, 等于该曲面所包围的所有电荷的代数和除以 0 . （与面外电荷无关，闭合曲面称为高斯面）
Φe3
q
0
0
q
S1 S2
q
S3
22
大学 物理
1.2 电通量 高斯定理
用高斯定理求解的电场强度步骤：
对称性分析；
根据对称性选择合适的高斯面； 1) 曲面通过场点，面积简单易算 2) 面上或部分曲面上各点的场强大小相等 3) 面上或部分曲面上各点的法线与场强方向 一致或垂直 应用高斯定理计算； 说明场强方向.

电通量和高斯定理

电通量和高斯定理

05 电通量与高斯定理的意义 和影响
对电磁学理论的意义
描述电场分布
建立电磁场理论
电通量是描述电场分布的重要物理量， 通过高斯定理，我们可以计算出空间 中任意区域的电场强度和电通量密度。
电通量与高斯定理是电磁场理论中的 基础概念，为后续的麦克斯韦方程组 等理论奠定了基础。
揭示电场性质
高斯定理揭示了电场的一个重要性质， 即电场线总是闭合的，这一性质对于 理解电场的产生和传播机制具有重要 意义。
散度定理法
利用散度定理计算电通量， 公式为：∮E⋅dS=∫E⋅dS。
微元法
将闭合曲面划分为若干个 小面元，分别计算每个面 元的电通量，最后求和得 到总电通量。
02 高斯定理的表述
定理的表述
高斯定理的表述
在封闭曲面S内，总电荷量Q等于该封闭曲面内电通量Φ的积分， 即 ∫∫Σ Q = ∫∫Σ dΦ。
电通量的物理意义
表示电场分布的特性
电通量的大小反映了电场在某个闭合 曲面上的分布情况，可以用来描述电 场的强弱和方向。
与电荷分布的关系
电通量的大小与电荷分布有关，电荷 分布的不同会导致电通量的变化。
电通量的计算方法
01
02
03
公式法
根据电场强度E和闭合曲 面S的面积S，计算电通量。 公式为：Φ=∫∫E⋅dS。
要点一
总结词
要点二
详细描述
高斯定理是求解电场的强大工具，通过合理选择高斯面可 以简化问题求解过程。
高斯定理表述为：“通过任意闭合曲面的电场强度通量等 于该闭合曲面所包围的电荷量与真空电容率的比值。”在 求解电场问题时，可以根据问题的对称性和电荷分布情况 选择合适的高斯面，从而将复杂的积分运算简化为简单的 代数运算。例如，在求解无限大均匀带电平面或球壳产生 的电场时，利用高斯定理可以快速得出结果。

9-3 电通量 高斯定理

9-3 电通量 高斯定理

A B
D C
B A
q
C
q e 6 0
D
例:如图所示，在正方体的某一顶点上有一点电 荷q，求通过面ABCD的电通量。 q
B A
C
D
q e 24 0
2. 当电场分布具有高度对称性时求场强分布 步骤： (1) 对称性分析，确定电场强度的大小和方向的 分布特征。 (2) 根据电场的对称性作高斯面，计算电通量。
S S S
0
q Ar4r dr
2 0
R
R
dr
r
r
(r R)
q 2 e E dS EdS E dS E 4r
S S S
0
q Ar 4r dr
2 0
r
第二种情形：电场呈现轴对称分布
例、如图所示，一无限长直均匀带电线，单位长 度的电量为 ，求其空间电场分布。
a. E是髙斯面各面元处的电场强度，是由全部电
0
q2
q4
课堂练习：当点电荷q4在曲面外移动时，通过闭合 曲面的电通量是否发生变化？P点的电场强度是否 发生变化？当点电荷q1在曲面内移动时又如何？
q4 q1 q2
P
q3
对电通量没有影响，但是，对P点的电场强度有影响。
三、高斯定理的应用
1 e E dS
R1 r R2
q1 4 / 3(r R ) EII 4r 3 0 4 / 3( R2 R )
2
R3
R1 I II
III
R2
R2 r R3
EIII 4r
2
0
q1
r R3
EIV
q1 q2 4 0 r 2

电通量_高斯定理

电通量_高斯定理
r<R
电量 ∑ qi = 0 由高斯定理 电量
P
r>R
∑q
i
= lλ
由高斯定理
E=0
λ E = 2π ε0 r
关于电通量
高斯定理的练习 1 Φ e = ∫ E • ds = ∑ qi
s
ε0
教材：P164 例1 P169 例2 P170例3 例4 P190 5-2 5-14 5-15 5-17 5-18 5-19 5-20 5-21
例.如图所示，一个带电量为 q 的点电荷位于正立方体的 A 角 上，则通过侧面 abcd 的电场 强度通量等于：
a
d
A
q
（A）q /6ε0 ; （B）q /12ε0 ； （C）q /24ε0 ; （D）q /36ε0 .
q
●q
●q
c
b
位于中 心 位于一顶点
过每一面的通量
[C] 若将此电荷移到正方体的一个顶点上，则通过整个正 方体表面的电场强度通量为 。q 8ε 0
3 r ρ 4 π 高斯定理 E 4 πr 2 = ε0 3
∑ qi ε0
ρr qr q 场强大小 E = = 场强大小 E = 3 4 πε 0 r 2 3ε 0 4 πε 0 R
q
∴E =
q e 2 r 4π ε0 r
r≥R
r≤R
oo RR
1 qr e, E= 3 r 4π ε0 R
5-4
电场强度通量
电场中的高斯定理
Eb
一．电场线（电场的图示法） c b 1、 E 方向：切线 E ∆N E a 2、 电场强度大小 E = ∆S a ⊥ 性质：不闭合；不相交； 定义：面积矢量 起于正、止于负。 S = Sn n 为面积的法向 闭合曲面的方向: 由曲面内指向曲面外 n n n n
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

习题 七 电通量、高斯定理
一、选择题
1、 一电场强度为→E 的均匀电场，→
E 的方向与x
则通过图中一半径为R 的半球面的电通量为（D ）
A 、πR 2
E B 、
2
1πR 2E C 、2πR 2
E D 、0
提示：电通量的几何意义：穿过该曲面的电场线的条数。

穿过该半球面的任一电场线必穿过两次，一次算正的，一次算负的，因半球面是有方向的，穿过该半球面的电场线的条数是代数量。

2、点电荷放在球形高斯面的中心处，下列哪种情况高斯面的电通量会发生变化（C ） A 、将另一点电荷放在高斯面外 B 、将球心处的点电荷移到高斯面内另一处 C 、将另一点电荷放进高斯面内 D 、改变高斯面半径大小 提示：由高斯定理知，高斯面的电通量只和面内的电荷有关。

3、真空中两平行带电平板相距为d ，面积为S ，且有d 2
<< S ,带电量分别为+q 和-q ，则两极板之间的作用力大小为（ D ） A 、2
024d
q F πε=
B 、2
0q F S ε=
C 、202q F S ε=
D 、2
02q F S
ε=
提示：A 板在B 板处的电场：000/222q S q
E S
σεεε=
== B 板上一电荷微元的受力：00()()
()22q q dF dq E dq dq S
S
εε===
B 板总受力：2
000()()2222S S S q
q
q
q F dF dq dq q S S S S εεεε====⋅=⎰⎰⎰ 4、如果一点电荷q 位于立方体一个顶点上，则通过不与该顶点相连的任一立方体侧面的电通量为（ D ） A 、0
B 、
εq
C 、
6εq D 、
24εq 提示：以该立方体为一个卦限，作一边长为该立方体边长2倍的立方体。

将大立方体的6个面分别分成4个小正方形，这样的小正方形共24个。

由
对称性，通过每个小正方形的电通量相等：
00
1112424
2424S
q q
E dS εεΦ=
Φ=⋅=
=⎰
总 5、下列说法正确的是（ A ）
A 、若高斯面上→
E 处处为0，则该面内必无净电荷（
0S
q E dS ε⋅==
⎰
内
，0q ⇒=内）
B 、若高斯面内无电荷，则高斯面上的→
E 必定处处为0（反例：处在均匀电场中的球面） C 、若高斯面上→
E 处处不为0，则高斯面内必有净电荷（反例：处在均匀电场中的球面） D 、若高斯面内有电荷，则高斯面上→
E 处处不为0（反例：两正的点电荷相距2R ，高斯面为以
一电荷为球心，以R 为半径的球面，则在两电荷连线和球面的交点处，场强为0） 二、填空题
1、一均匀带有电量为Q ，长为l 的直线，以直线中心为球心，R （R >l ）为半径作球面，则通过该
球面的电通量为
Q
ε，在带电直线的延长线上与球面的交点处的场强大小为
0422Q
l l R R πε⎛⎫⎛⎫
+- ⎪⎪
⎝
⎭⎝⎭。

提示：第一空：该带电线完全被球面所包围，由高斯定理可知结果。

第二空：建立Or 坐标系，坐标轴位于带电线上，坐标原点位于带电线的中心，方向沿球面的半径向外。

在带电线上取微元dQ 。

22
00(/)4()4()
dQ Q l dr
dE R r R r πεπε=
=-- /2
/2
2
/2
/2
00(/)4()422l l l l Q l dr
Q
E dE l l R r R R πεπε++--===
-⎛
⎫⎛⎫+- ⎪⎪
⎝
⎭⎝⎭⎰
⎰
2、由一半径为R 、均匀带有电量Q 的球面，产生的电场空间，在距离球心r 处的电场强度为：当
r<R 时，E= 0 ，当r>R 时，E=
2
04Q r πε。

提示：参考课件有关例题。

3、由一半径为R 的无限长均匀带电圆筒面产生的电场空间，与圆筒中心轴线相距为r 处的电场强
度大小为：当r<R 时，E= 0 当r>R 时，E=r
02πελ
（已知圆筒面上带电线密度为λ）。

提示：参考课件有关例题。

4、由一半径为R ，电荷体密度为ρ的无限长均匀带电圆柱体产生的电场空间，当r<R 时，E=
2r ρε，当r>R 时，E=r
R 02
2ερ。

提示：由高斯定理：
(2)S
q E dS E rh πε⋅==
⎰
内
200
2
2000(),(),()222(),(),()22r
r h r R r R hr q E hr R
R h r R r R r hr ρρπεπεπερρπεπε⎧⎧<<⎪⎪⎪⎪⇒===⎨⎨⎪⎪
>>⎪⎪⎩⎩
内 省略了一些步骤，可参照课件学习！
5、一无限大均匀带电面密度为σ的平面上有一半径为R 的圆面型空缺，则在空缺的中垂线上与圆
面相距为d 处的电场强度大小为
2
2
02d
R d
+εσ。

提示：均匀带电圆环在其轴线上的电场：223/2
04()
qx
E x R πε=
+ 把带电面划分成无数带电圆环，每一带电圆环的电场：
223/2223/2223/2
000()()(2)4()4()4()dq d dS d rdr d
dE d R d R d R σσππεπεπε⋅=
==
+++
带电面的电场：223/20(2)4()R
rdr d E dE d R σππε∞
⋅==
=+⎰⎰
或用补偿法，直接用无限大均匀带电面的场减均匀带电圆盘的场。

三、计算题
1、一对无限长的同轴直圆筒，半径分别是R 1和R 2（R 1<R 2）,筒面上都均匀带电，沿轴线单位长度
的电量分别为λ1和λ2，试求其空间的电场强度分布。

解：取一半径为r ，长度为L 的同轴圆筒面为高斯面，应用高斯定理，
(2)S
q E dS E rL πε⋅==
⎰
内
1
011112120001212
22000,()20,(),(),()222(),(),()22r R rL r R q L E R r R R r R rL rL r L r R r R rL r
πελλπεπεπελλλλπεπε⎧⎧
<⎪⎪<⎪⎪⎪⎪⇒==<<=<<⎨⎨⎪⎪
⎪⎪++>>⎪⎪
⎩⎩内
2、内外半径分别为R 1、R 2的均匀带电厚球壳，电荷体密度为ρ，求空间各处的电场强度。

解：取一半径为r 的同心球面为高斯面，应用高斯定理，
20
4S
q E dS E r πε⋅=⋅=
⎰
内
()()12
013333111212222
00033
332
12122022
00
,()40,()4433,(),()44344,()333,()4r R r r R r R r R q E R r R R r R r r r R R R R r R r r R r περππρπεπεερρππεπε⎧<⎪⎧⎪⎪
<⎪⎪⎛⎫
-⎪⎪ ⎪-⎪⎪⎝⎭==<<=<<⎨⎨⎪⎪
⎪⎪⎛⎫--⎪⎪ ⎪>⎝⎭⎪⎪>⎩⎪⎩
内 3、厚度为d 的无限大均匀带电平板，若电荷体密度为ρ，求空间各处的电场强度。

解：方法一： 参考课件有关例题。

由无限大均匀带电平面周围空间的电场
2E σ
ε=
可计算得出： ()()
2,02,02x d
x d E d x x d ρερε⎧-<<⎪
⎪=⎨
⎪<>⎪⎩或，方向均远离对称面。

提示：1）dx σρ=；
2）在板外，所有无限大带电面的电场同向；在板内，考察点两侧的无限大带电面的电场反向；
方法二：利用高斯定理。

为方便见，此次坐标原点定在板的对称面上。

00,2,22x d x E d d x ρερε⎧⎛⎫
<⎪ ⎪
⎝
⎭⎪=⎨
⎛⎫
⎪> ⎪⎪⎝
⎭⎩，方向均远离对称面。

（ 提示：参考课件有关例题。

）
（注：本资料素材和资料部分来自网络，仅供参考。

请预览后才下载，期待您的好评与关注！）
x。