2.3.1-4电通量和高斯定理

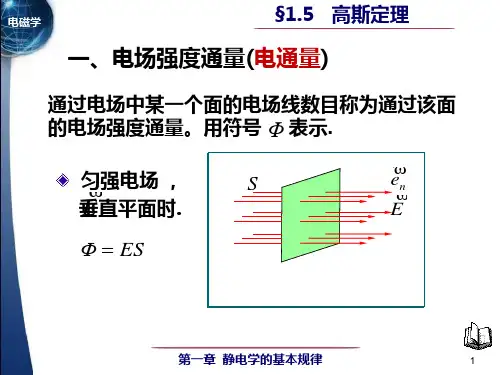
大学物理复习第四章知识点总结大学物理复习第四章知识点总结一．静电场：1.真空中的静电场库仑定律→电场强度→电场线→电通量→真空中的高斯定理qq⑴库仑定律公式：Fk122err适用范围：真空中静止的两个点电荷F⑵电场强度定义式：Eqo⑶电场线：是引入描述电场强度分布的曲线。

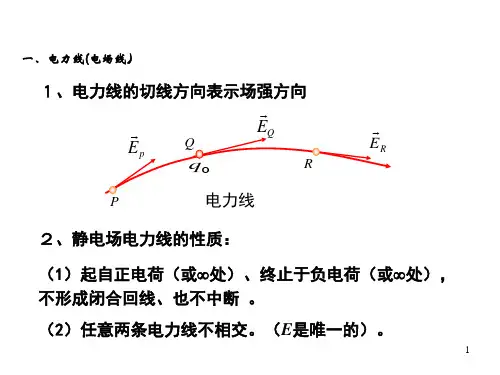
曲线上任一点的切线方向表示该点的场强方向，曲线疏密表示场强的大小。

静电场电场线性质:电场线起于正电荷或无穷远，止于负电荷或无穷远，不闭合，在没有电荷的地方不中断，任意两条电场线不相交。

⑷电通量：通过任一闭合曲面S的电通量为eSdS方向为外法线方向1EdS⑸真空中的高斯定理：eSoEdSqi1int只能适用于高度对称性的问题：球对称、轴对称、面对称应用举例：球对称：0均匀带电的球面EQ4r20(rR)(rR)均匀带电的球体Qr40R3EQ240r(rR)(rR)轴对称：无限长均匀带电线E2or0(rR)无限长均匀带电圆柱面E(rR)20r面对称：无限大均匀带电平面EE⑹安培环路定理：dl0l2o★重点：电场强度、电势的计算电场强度的计算方法：①点电荷场强公式+场强叠加原理②高斯定理电势的计算方法：①电势的定义式②点电荷电势公式+电势叠加原理电势的定义式：UAAPEdl(UP0)B电势差的定义式：UABUAUBA电势能：WpqoPP0EdlEdl(WP00)2.有导体存在时的静电场导体静电平衡条件→导体静电平衡时电荷分布→空腔导体静电平衡时电荷分布⑴导体静电平衡条件:Ⅰ.导体内部处处场强为零,即为等势体。

Ⅱ.导体表面紧邻处的电场强度垂直于导体表面，即导体表面是等势面⑵导体静电平衡时电荷分布:在导体的表面⑶空腔导体静电平衡时电荷分布:Ⅰ.空腔无电荷时的分布：只分布在导体外表面上。

Ⅱ.空腔有电荷时的分布(空腔本身不带电，内部放一个带电量为q的点电荷)：静电平衡时，空腔内表面带-q电荷，空腔外表面带+q。

3.有电介质存在时的静电场⑴电场中放入相对介电常量为r电介质，电介质中的场强为：E⑵有电介质存在时的高斯定理：SDdSq0,intE0r各项同性的均匀介质D0rE⑶电容器内充满相对介电常量为r的电介质后，电容为CrC0★重点：静电场的能量计算①电容：②孤立导体的电容C4R电容器的电容公式C0QQUUU举例：平行板电容器C圆柱形电容器C4oR1R2os球形电容器CR2R1d2oLR2ln()R1Q211QUC(U)2③电容器储能公式We2C22④静电场的能量公式WewedVE2dVVV12二.静磁场：1.真空中的静磁场磁感应强度→磁感应线→磁通量→磁场的高斯定理⑴磁感应强度：大小BF方向：小磁针的N极指向的方向qvsin⑵磁感应线：是引入描述磁感应强度分布的曲线。

高斯定理数学高斯定理，又称为高斯-奥斯特罗格雷定理（Gauss-Ostrogradsky theorem），是描述向量场通过曲面的流量密度与该曲面边界上环绕该曲面沿法向量方向的一圈线积分之间的关系的定理，是矢量分析的重要内容之一，也是工程中常用的理论。

$$\oint_S \textbf{F} \cdot \textbf{n} dS = \iiint_V \nabla \cdot \textbf{F} dV$$$\textbf{F}$ 表示某个向量场，$S$ 表示一个逐片光顺的曲面，$V$ 为该曲面所包围的立体。

$\textbf{n}$ 表示曲面上某一点的法向量，$\nabla \cdot \textbf{F}$ 为向量场 $\textbf{F}$ 的散度。

该式中左边表示 $\textbf{F}$ 向外通过曲面 $S$ 的流量密度。

左侧积分的意思是，对于曲面 $S$ 的每一点，对由该点到曲面外侧的垂直方向的投影所围成的小面积$dS$ 进行积分，得到整个曲面通过的总流量密度。

右边表示 $\textbf{F}$ 在立体$V$ 中的散度。

右侧积分的意思是，对于立体 $V$ 中的每一点，计算该点的散度，然后对整个立体进行积分，得到散度在整个立体中的总量。

高斯定理适用于任意的向量场，包括电场、磁场等。

它可以用来推导一些物理方程，并在基础数学领域中起到重要作用。

对于电场，高斯定理可以用来计算电通量，即电场向外通过一个立体的总电量。

对于静电场和恒定电场来说，高斯定理可以推导出库仑定律。

对于磁场，高斯定理可以用来推导出安培环路定理。

高斯定理在物理学和工程学中有非常广泛的应用，是理解和解决问题的重要工具之一。

高斯定理的证明可以通过追踪微小体积元素上的向外流量来完成。

假设该体积元素为$\Delta V$，体积元素表面上带有一小片面积为 $\Delta S$，该片面积的法向量表示为$\textbf{n}$。

向量场 $\textbf{F}$ 在该面积上的流量为 $\textbf{F} \cdot\textbf{n} \Delta S$，如果对所有该体积元素上的面积进行累计，则构成了整个曲面的流量，并得到了高斯定理的左侧积分：$$\oint_S \textbf{F} \cdot \textbf{n} dS$$接下来，可以通过施加散度定理来将该定理转化为该向量场的散度在这个立方体中的积分：证明中还需要使用到一些高等数学的知识，如积分中值定理等，具体证明过程相对复杂。

第一章 电磁现象的普遍规律§1.1 电荷与电场1、库仑定律（1）库仑定律如图1-1-1所示，真空中静止电荷'Q 对另一个静止电荷Q 的作用力F 为()'3''041r r rr Q Q F --=πε （1.1.1）式中0ε是真空介电常数。

（2）电场强度E静止的点电荷'Q 在真空中所产生的电场强度E为()'3''41r r r r Q E --=πε （1.1.2）（3）电场的叠加原理N 个分立的点电荷在r 处产生的场强为()'13'0'4iNi i i r r r r Q E --=∑=πε （1.1.3）体积V 内的体电荷分布()'rρ所产生的场强为()()'3'''041r r r r dV r E V--=⎰ρπε （1.1.4）式中'r 为源点的坐标，r为场点的坐标。

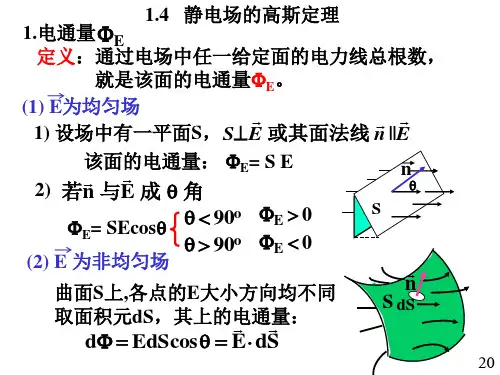
2、高斯定理和电场的散度高斯定理：电场强度E穿出封闭曲面S 的总电通量等于S 内的电荷的代数和)(∑ii Q 除以0ε。

用公式表示为∑⎰=⋅iiSQS d E 01ε （分离电荷情形） （1.1.5）或⎰⎰=⋅VSdV S d E ρε01（电荷连续分布情形） （1.1.6）其中V 为S 所包住的体积，S d为S 上的面元，其方向是外法线方向。

应用积分变换的高斯公式⎰⎰⋅∇=⋅VSdV E S d E（1.1.7）由（1.1.6）式可得静电场的散度为ρε01=⋅∇E 3. 静电场的旋度由库仑定律可推得静电场E的环量为0=⋅⎰Ll d E（1.1.8）应用积分变换的斯托克斯公式⎰⎰⋅⨯∇=⋅SLS d E l d E从（1.1.8）式得出静电场的旋度为0=⨯∇E（1.1.9）§1.2 电流和磁场1、电荷守恒定律不与外界交换电荷的系统，其电荷的代数和不随时间变化。

对于体积为V ，边界面为S 的有限区域内，有⎰⎰-=⋅V S dV dtdS d J ρ （1.2.1） 或0=∂∂+⋅∇tJ ρ（1.2.2）这就是电荷守恒定律的数学表达式。

静电场中的高斯定理：高斯定理是静电学中的一个重要定理, 它反映了静电场的一个基本性质, 即静电场是有源场, 其源即是电荷。

可表述为: 在静电场中, 通过任意闭合曲面的电通量, 等于该闭合曲面所包围的电荷的代数和的1/ε倍, 与闭合曲面外的电荷无关。

表达式为01()1/n i i S E ds q φε==∙=∑⎰⎰ （1）高斯定理是用来求场强E 分布, 定理中, S 是任意曲面, 由于数学水平的限制, 要由高斯定理计算出E,则对由场的分布有一定的要求, 即电荷分布具有严格的对称性( 若电荷分布不对称性即不是均匀的, 引起电场分布不对称, 不能从高斯定理求空间场强分布,高斯定理当然仍是成立的) , 由于电荷分布的对称性导致场强分布的对称性, 场强分布的对称性应包括大小和方向两个方面。

典型情况有三种:1) 球对称性, 如点电荷, 均匀带电球面或球体等;2) 轴对称性, 如无限长均匀带电直线, 无限长均匀带电圆柱或圆柱面, 无限长均匀带电同轴圆柱面3) 面对称性, 如均匀带电无限大平面或平板,或者若干均匀带电无限大平行平面。

根据高斯定理计算场强时, 必须先根据电荷分布的对称性, 分析场强分布的对称性; 再适当选取无厚度的几何面作为高斯面。

选取的原则是:○1 待求场强的场点必须在高斯面上;○2 使高斯面的各个部分或者与E 垂直, 或者E 平行;○3 与E 垂直的那部分高斯面上各点的场强应相等;○4 高斯面的形状应是最简单的几何面。

最后由高斯定理求出场强。

高斯定理说明的是通过闭合曲面的电通量与闭合曲面所包围的所有电荷的代数和之间的关系, 即闭合曲面的总场强E 的电通量只与曲面所包围的电荷有关, 但与曲面内电荷的分布无关。

但闭合曲面上的电场强度却是与曲面内外所有电荷相联系的,是共同激发的结果。

下面举一些例子来说静电场中高定理的应用：例1：一半径为R 的带电球体，其电荷体密度分布为()Ar r R ρ=≤，0()r R ρ=>，A 为大于零的常量。

电学高斯定理-概述说明以及解释1.引言1.1 概述：电学高斯定理，又称高斯电场定理，是电学领域中一个非常重要的定理，它描述了电场在闭合曲面上的总通量与在该曲面内所有点电荷的代数和之间的关系。

通过高斯定理，我们可以更加深入地理解电场的性质和分布。

在本文中，我们将对电学高斯定理进行详细探讨，包括其概念、数学表达以及应用。

通过对电场的分析和计算，我们可以更好地理解高斯定理在电学领域中的重要性和实际应用价值。

同时，我们也将展望未来高斯定理的发展方向，探讨其在电学研究中的潜在应用和意义。

通过本文的学习，读者将能够更加全面地认识和理解电学高斯定理，为其在实际工程和科研中的应用提供帮助和指导。

1.2 文章结构本文将从引言部分开始，首先概述电学高斯定理的重要性和应用价值，然后介绍文章的结构安排。

接着将进入正文部分，详细讨论电学高斯定理的概念、数学表达以及其在现实生活中的应用情况。

最后，结论部分将总结电学高斯定理的重要性和在电学领域的应用，同时展望未来高斯定理的发展趋势。

整篇文章将全面介绍电学高斯定理，帮助读者更好地理解和应用这一重要理论。

1.3 目的电学高斯定理作为电磁学中的重要定律之一，其目的在于帮助我们理解电荷在电场中的行为规律。

通过深入研究高斯定理，我们可以更好地理解电场分布情况，预测电荷的运动轨迹，并解决复杂电学问题。

此外，掌握电学高斯定理还可以为我们提供一种便捷的计算电场强度的方法，简化电场分析的过程。

通过对高斯定理的掌握，我们可以更高效地解决工程中的电学问题，提高电学学科的研究水平和工程应用技术。

因此，本文旨在深入探讨电学高斯定理的概念、数学表达和应用，帮助读者更好地理解电场的特性，拓展电学知识，为电学领域的学习和研究提供有益的参考。

2.正文2.1 电学高斯定理的概念电学高斯定理，也称为高斯通量定理，是电学领域中的一个重要定理。

它描述了电场通过任意闭合曲面的总通量等于该曲面内的电荷总量的1/ε₀倍，其中ε₀为真空介电常数。

静电场中的高斯定理教学探讨【摘要】静电场中的高斯定理是电磁学中的重要定理之一，本文从高斯定理的定义和原理入手，介绍了它的应用范围和在静电场中的具体应用。

通过分析高斯定理的证明方法和实际案例，探讨了其在解决电场问题中的重要性和实用性。

总结了静电场中高斯定理教学的重要性和应用意义。

通过本文的学习，读者可以更深入地了解静电场中的高斯定理，掌握其理论基础和实际应用，为电磁学的学习和研究提供了有力支持。

【关键词】静电场、高斯定理、教学探讨、定义、原理、应用范围、证明方法、实际案例、总结1. 引言1.1 静电场中的高斯定理教学探讨静电场中的高斯定理是物理学中非常重要的原理之一，它可以帮助我们更好地理解静电场的性质和特点。

在教学过程中，我们需要深入探讨高斯定理的定义和原理，探讨它的应用范围以及在静电场中的具体应用。

我们也需要讨论高斯定理的证明方法和实际案例，帮助学生更好地理解和应用这一定理。

在教学探讨的过程中，我们可以引导学生思考和讨论，激发他们对物理学知识的兴趣，并培养他们的探究精神和创新能力。

通过对静电场中的高斯定理的教学探讨，可以让学生在学习物理学知识的更好地理解科学原理，并将其运用到实际问题中。

将会成为教学中的重要内容，帮助学生更好地掌握物理学知识，提高他们的学习水平和能力。

2. 正文2.1 高斯定理的定义和原理高斯定理是电磁学中非常重要的定理之一，它描述了电场的分布与电荷的关系。

高斯定理表明，通过一个封闭曲面的电通量正比于该曲面内包围的总电荷量。

具体来说，高斯定理可以表示为\[\oint \vec{E} \cdot d\vec{A} =\frac{Q_{\text{enc}}}{\varepsilon_0}\]\oint \vec{E} \cdot d\vec{A} 表示曲面S上电场\vec{E}的法向分量与微元面积d\vec{A}的乘积总和，Q_{\text{enc}} 表示曲面S内包围的总电荷量，\varepsilon_0 是真空介电常数。