《运筹学》使用Excel求解线性规划问题
- 格式:doc
- 大小:309.00 KB
- 文档页数:6


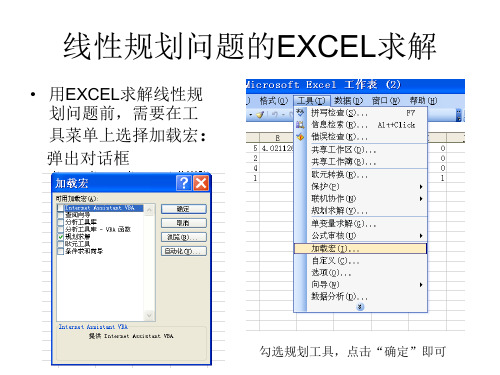
用EXCEL求解线性规划
要用EXCEL求解线性规划问题,需要遵循以下步骤:
1. 给定问题中的约束条件和目标函数。
2. 打开EXCEL,建立一个新的工作表。
3. 在工作表中输入问题的约束条件和目标函数。
在输入目标函数时,需要将所有项移动到等号左侧,使它成为一个线性方程。
需要注意将不等式约束条件转化为等式约束条件,可以通过添加松弛变量来实现。
4. 使用EXCEL的“规划”工具,在工具栏中点击“数据”-“分
析”-“规划器”,打开“规划器”。
5. 在“规划器”中,选择需要优化的目标单元格,在“约束条件”
中输入所有约束条件所在的单元格,设置变量单元格的范围。
6. 可以在“选项”中添加其他约束条件。
例如,可以设定变量的整数或二元特性等。
7. 单击“求解”按钮,EXCEL将自动求解最优解,并输出最优
值和变量值。
需要注意的是,线性规划问题求解的结果是一个数值,而不是图形。
因此,需要谨慎分析问题以确保从数值结果中得到了正确的结论。


利用线性回归方法求解生产计划方法一:1、建立数学模型:①设变量:设生产拉盖式书桌x台,普通式书桌y台,可得最大利润②确定目标函数及约束条件目标函数:y=max+115P90x约束条件:200x .....................⑴+y10≤20x .....................⑵4≤+y16128x .....................⑶+y1015≤220yx ..........................⑷,≥2、在Excel中求解线性规划①首先,如图1所示,在Excel工作表格输入目标函数的系数、约束方程的系数和右端常数项:图1②将目标方程和约束条件的对应公式输入各单元格中F2=MMULT(B6:C6,F6:F7);F3=MMULT(B3:C3,F6:F7);F2=MMULT(B4:C4,F6:F7);F2=MMULT(B5:C5,F6:F7);出现图2样式:图2线性规划问题的电子表格模型建好后,即可利用“线性规划”功能进行求解。
选择“工具”→“规划求解”出现“规划求解参数”窗口,如图3所示:图3在该对话框中,目标单元格选择F2,问题类型选择“最大值”,可变单元格选择F6:F7,点击“添加”按钮,弹出“添加约束条件”窗口,如图4所示:图4根据所建模型,共有4个约束条件,针对约束(1):2002010≤+y x ,左端“单元格所引用位置”选择F3,右端“约束值”选择D3,符号类 型选择“<=”,同理继续添加约束(2)(3)(4),完成后选择“确定”,回到“规划求解参数”对话框,如5图所示:图5④点击“选项”按钮,弹出“规划求解选项”对话框,选择“采用线性模型”和“假定非负”两项,如图6所示:图6⑤点击“确定”→“求解”,选择“运算结果报告”“敏感性报告”“极限值报告”三项,最后点击“确定”,输出结果: 运算结果报告:敏感性报告:极限报告:方法二:1、建立数学模型设生产拉盖式书桌x 台,普通式书桌y 台,总利润为Z 元 确定目标函数及约束条件 目标函数:y x Z 90115max += 约束条件:⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤+0,22010151281642002010..y x y x y x y x t s 2、在Excel 中规划求解在Excel 中建立线性规划模型,如图1所示:图11)在E2中输入“=B2*B6+C2*C6”如图2所示,同理 E3=B3*B6+C3*C6E4=B4*B6+C4*C6B7=B5*B6+C5*C6图22)单击“工具”菜单下的“规划求解”,在弹出的“规划求解参数”对话框输入各项参数:✓目标单元格选择B7✓问题类型选择“最大值”✓可变单元选择B6:C6✓约束条件选择B6:C6≥0;E2:E4≤D2:D4参数设置完毕,如图3:图33)点击“选项”,弹出“规划求解选项”对话框,选择“采用线性模型”、“假定非负”和“显示迭代结果”,说明要求求解的问题是线性模型且所求的变量必须为非负,如图4所示:图44)点击“确定”→“求解”,选择“运算结果报告”“敏感性报告”“极限值报告”三项,最后点击“确定”,输出结果:运算结果报告:敏感性报告:极限值报告:。



利用Excel求解线性规划问题线性规划问题的求解有很多方法,也有很多工具。
比如常用的Matlab、Lingo,记得参加数学建模的时候就是用的Lingo解决线性规划问题的。
本文主要讲解如何使用Excel求解线性规划问题,Excel本身是没有计算线性规划问题能力的,因此我们首先要加载相应的宏定义。
一、加载宏定义(不同版本的加载方式有所不同):Excel 2003:单击“工具”菜单,然后单击“加载宏”,选择“规划求解”点击确定。
Excel 2007:方法一:用快捷键。
先按Alt+T,再按I键,即可打开加载宏对话框。
方法二:单击“Office按钮→Excel 选项→加载项”,确保“管理”右侧下拉列表中的选项是“Excel 加载项”,单击“转到”按钮即可。
Excel 2010:直接在功能区中选择“开发工具”选项卡,在“加载项”组中单击“加载项”命令,选择“规划求解”点击确定。
注意:如果功能区中没有“开发工具”选项卡,可以通过自定义功能区来显示“开发工具”选项卡:单击“文件→选项→自定义功能区”,然后在右侧区域中勾选“开发工具”并单击“确定”。
二、初始化数据(以Excel 2010为例,其他版本大同小异):比如我们要计算的线性规划问题如下:那么,我们可以构造如下的表格数据。
其中,B2:F2为待求的值Xi,B3:F3为目标函数的系数,B4:F4、B5:F5、B6:F6为约束条件的系数。
在G3单元格中输入公式=$B$2*B3+$C$2*C3+$D$2*D3+$E$2*E3+$F$2*F3,并将鼠标放到单元格的右下角会变成黑色十字架,向下拖拽复制单元格公式到G4、G5、G6单元格。
然后,单击“数据”选项卡,单击“规划求解”打开“规划求解参数”对话框。
∙修改“设置目标”为$G$3,即最优解下目标函数的值z所在的单元格。
∙选择是求最大值,还是最小值。
∙“可变单元格”指的是最优解取值变量所在的单元格。
∙“遵守约束”指的是约束条件中对各变量的约束情况。

第2章 线性规划的计算机求解及应用举例§1线性规划模型在电子表格中的布局线性规划模型在电子表格中布局的好坏关系到问题可读性和求解方便性的高低。
本节以第一章中的例1(资源分配问题)为例来说明一下如何在电子表格中描述线性规划模型,让我们回顾一下第一章中例1的数学模型:Max 1243Z x x =+s.t. 1212126282318,0x x x x x x ≤⎧⎪≤⎪⎨+≤⎪⎪≥⎩ (2.1)一般来说,在与问题相关的表格的基础上稍加调整就可以在电子表格中形成一个十分清晰的模型描述。
我们以表1-1为基础在Excel 电子表格中将上述问题描述如图2-1。
§2用Excel规划求解工具求解线性规划模型Excel 中有一个工具叫规划求解,可以方便地求解线性规划模型。
“规划求解”加载宏是Excel 的一个可选加载模块,在安装Excel 时,只有在选择“定制安装”或完全安装时才可以选择装入这个模块。
如果你现在的Excel 窗口菜单栏的“工具”菜单中没“规划求解”选项,可以通过“工具”菜单的“加载宏”选项打开“加载宏”对话框来添加“规划求解”(见图2-2)。
在应用规划求解工具以前,要首先确认在Excel 电子表格中包括决策变量、目标函数、约束函数三种信息的单元格或单元格区域。
图2-1中的电子表格中就已经有了这部分内容:决策变图2-1 资源分配问题的模型在Excel 电子表格的布局及公式图2-2 加载宏对话框量在C9和D9单元格中;目标函数的系数在第8行;约束函数在第5、6和7行。
因为我们不知道决策变量的值是多少,所以就在决策变量所在的单元格中填上初始值“0”,当然也可以什么都不填,系统会默认它为0,在求解以后Excel会自动将它们替换成决策变量的最优解。
下面我们接着上节的内容用Excel规划求解将第一章例1的资源分配问题解一遍。
首先将要求解模型的所有相关信息和公式像图2-1那样填入电子表格中后,再选取[工具] | [规划求解]命令后,弹出图2-3所示的“规划求解参数”对话框。

实验三、用Excel求解线性规划模型线性规划问题用手工求解工作量很大,而且没有较高的数学基础很难理解其计算过程和方法,但是借助Excel“规划求解”工具,就能轻而易举地求得结果。
Excel最多可解200个变量、600个约束条件的问题。
下面我们以一实例介绍利用Excel规划求解工具怎样快速解决具体的经济决策问题。
一、实验目的1、掌握如何建立线性规划模型。
2、掌握用Excel求解线性规划模型的方法。
3、掌握如何借助于Excel对线性规划模型进行灵敏度分析,以判断各种可能的变化对最优方案产生的影响。
4、读懂Excel求解线性规划问题输出的运算结果报告和敏感性报告。
二、实验内容1、[工具][规划求解]命令规划求解加载宏是Excel的一个可选安装模块,在安装Excel时,只有在选择“完全/定制安装”时才可选择装入这个模块。
在安装完成进入Excel后还要用[工具][加载宏]命令选中“规划求解”,以后在[工具]菜单下就增加了一条[规划求解]命令。
使用[规划求解]命令的一般步骤为:第一步:在选取[工具][规划求解]命令后,弹出图1所示“规划求解参数”对话框,其中各选项说明如表1。
图1“规划求解参数”对话框选项名说明设置目标单元格选取计算问题的目标函数,并含有计算公式的单元格等于按问题目标进行选择。
如利润问题,选取“最大值”可变单元格决策变量所在各单元格、不含公式,可以有多个区域或单元格约束增加、修改、删除各个约束等式或不等式,一个一个地与图2切换填入或修改添加选择后弹出图2所示对话框更改选择后弹出图3所示对话框删除删除所选定的约束条件选项决定采用线性模型还是非线性模型求解约束条件中的单元格引用位置,可从键盘直接录入,也可用鼠标拖放选取。
图2图3第二步:完成图1所示的一切填入项目后,单击“选项”按钮,在弹出的“规划求解选项”对话框中若是线性模型则选取“采用线性规模”选项按钮,再单击“确定”按钮回到图1。
图4第三步:在图1中单击“求解”按钮,经计算完成后弹出“规划求解结果”对话框(图5)。
《实用运筹学》上机实验指导课程名称:运筹学/Operations Research实验总学时数:60学时一、实验教学目的和要求本实验与运筹学理论教学同步进行。
目的:充分发挥Excel软件这一先进的计算机工具的强大功能,改变传统的教学手段和教学方法,将软件的应用引入到课堂教学,理论与应用相结合。
丰富教学内容,提高学习兴趣。
要求:能用Excel软件中的规划求解功能求解运筹学中常见的数学模型。
二、实验项目名称和学时分配三、单项实验的内容和要求实验一线性规划(-)实验目的:安装Excel软件“规划求解”加载宏,用Excel软件求解线性规划问题。
(二)内容和要求:安装并启动软件,建立新问题,输入模型,求解模型,结果的简单分析。
(三)实例操作:求解习题1.1。
(1)建立电子表格模型:输入数据、给单元格命名、输入公式等;(2)使用Excel软件中的规划求解功能求解模型;(3)结果分析:如五种家具各生产多少?总利润是多少?哪些工序的时间有剩余,并对结果提出你的看法;(4)在Excel或Word文档中写实验报告,包括线性规划模型、电子表格模型和结果分析等。
案例1 生产计划优化研究某柴油机厂年度产品生产计划的优化研究。
某柴油机厂是我国生产中小功率柴油机的重点骨干企业之一。
主要产品有2105柴油机、x2105柴油机、x4105柴油机、x4110柴油机、x6105柴油机、x6110柴油机,产品市场占有率大,覆盖面广。
柴油机生产过程主要分成三大类:热处理、机加工、总装。
与产品生产有关的主要因素有单位产品的产值、生产能力、原材料供应量与生产需求情况等。
每种产品的单位产值如错误!未找到引用源。
所示。
表 C-1 各种产品的单位产值为简化问题,根据一定时期的产量与所需工时,测算了每件产品所需的热处理、机加工、总装工时,如表 C-2所示。
表 C-2 单位产品所需工时同时,全厂所能提供的总工时如表 C-3所示。
表 C-3 各工序所能提供的总工时产品原材料主要是生铁、焦碳、废钢、钢材四大类资源。


《运筹学》课程实验报告
班别数学1410 姓
名杨欢
学号1101141020 实验室号28实验室
日期2015年12月4日组号计算机号52 实验
名称
Excel求解线性规划问题成绩评定
所用
软件Excel
老师签名
实
验
目的或要求能够熟练建立线性规划数学模型,熟练掌握Excel求解线性规划问题的应用。
通过实验进一步掌握运筹学有关方法原理、求解过程,提高分析问题和解决问题。
实
验过
程、心
得或体会实验过程:
1.建立线性规划数学模型。
Max z=2x1+3x2
s.t. 2x1+2x2<=12
4x1 <=16
5x2<=15
X1 , x2>=0
2.在Excel中建立线性规划问题。
3.应用Excel求解该规划问题。
(1)单击“工具”菜单“规划求解”,出现“规划求解参数”对话框:依次在“设置目标单元格”输入“目标值”、“可变单元格”中输入“变量”,选中“最大值”单选按钮;
(2)单击“规划求解参数”对话框中“添加”按钮,出现“添加约束”对话框,按对话框要求依次添加约束条件“资源一(二、三……)实际使用量<=资源一(二、三……)提供量”,单击“确定”按钮。
(3)单击“规划求解参数”对话框中“选项”按钮,出现“规划求解选项”对话框,选中“采用线性模型”和“假定非负”多选按钮后单击“确定”按钮。
(4)单击“规划求解参数”对话框中“求解”按钮,出现“规划求解结果”对话框,单击“确定”按钮后得到求解结果。
实验结论:
当x1=3,x2=3时,目标函数最大,为15。



荆楚理工学院运筹学实训实验室实验报告 课程名称:运筹学实训 专业:数学与应用数学实验题目 利用excel 实现单纯形表计算学生姓名 李武阳赵星浩王 铖学 号 2016409010113 2016409010114 2018ZSB091107 班级 16级数学与应用数学1班 指导教师 张玲 实验日期 2018.10.10 成绩一、实验目的与要求:1、理解单纯形算法的原理和基本过程2、能利用EXCEL 实现单纯形表计算二、实验任务:利用excel 实现下列线性规划问题的单纯形算法的过程1、在excel 中输入单纯形表;2、在表格中计算检验数;3、在表格中实现换基运算;4、在表格中实现初等行变换。
用单纯形法解决下面线性规划问题(用大M 法);⎪⎪⎩⎪⎪⎨⎧≥≥≥+≥+++-=0,,0-222-622max 3213231321321x x x x x x x x x x x x x Z三、实验步骤和结果,(给出主要过程的文字说明,包含代码、图、表)1、在excel 表格中输入题目数据;2、计算检验数,找出最大的检验数并进基X2退基X9;3、重复换基,当人工变量全部退基时候,X4的检验数为1.25理应进基,但X4所在列的系数均小于等于0,即线性规划问题有无界解。
(具体计算过程如下所示)由上面的结果可以得到:此线性方程组的可行域是无界的,所以该线性方程组无有限解。
四、实验总结(对实验过程进行分析,总结实验过程中出现的问题、体会和收获)本次实验在excel表格中完成,所以容易因为看错数字而出错,单纯形表的运算性质决定在一步错之后往往需要重新算,所以比较费时费力,我们在计算时要注意每个量及每一步的进基和出基的选择。
但是我们可以利用这个方法可以解决实际问题中比较复杂的一些线性规划问题,特别是一些手工计算难以求解的问题。
五附录Excel。
第三节 使用Excel 求解线性规划问题
利用单纯形法手工计算线性规划问题是很麻烦的。
office 软件是一目前常用的软件,我们可以利用office 软件中的Excel 工作表来求解本书中的所有线性规划问题。
对于大型线性规划问题,需要应用专业软件,如Matlab ,Lindo ,lingo 等,这些软件的使用这里我们不作介绍,有需要的,自己阅读有关文献资料。
用Excel 工作表求解线性规划问题,我们需要先设计一个工作表,将线性规划问题中的有关数据填入该工作表中。
所需的工作表可按下列步骤操作:
步骤1 确定目标函数系数存放单元格,并在这些单元格中输入目标函数系数。
步骤2 确定决策变量存放单元格,并任意输入一组数据。
步骤3 确定约束条件中左端项系数存放单元格,并输入约束条件左端项系数。
步骤4 在约束条件左端项系数存放单元格右边的单元格中输入约束条件左端项的计算公式,计算出约束条件左端项对应于目前决策变量的函数值。
步骤5 在步骤4的数据右边输入约束条件中右端项(即常数项)。
步骤6 确定目标函数值存放单元格,并在该单元格中输入目标函数值的计算公式。
例 建立如下线性规划问题的Excell 工作表:
12
121
21212max 1502102310034120..55150
,0z x x x x x x s t x x x x =++≤⎧⎪+≤⎪⎨+≤⎪⎪≥⎩
解:下表是按照上述步骤建立的线性规划问题的Excell 工作表。
其中:
D4=B2*B4+C2*C4, D5=B2*B5+C2*C5 , D6=B2*B6+C2*C6, C7= B2*B1+C2*C1 。
建立了Excel 工作表后,就可以利用其中的规划求解功能求相应的线性规划问题的解。
求解步骤如下:
步骤1 单击[工具]菜单中的[规划求解]命令。
步骤2 弹出[规划求解参数]对话框,在其中输入参数。
置目标单元格文本框中输入目标单元格;[等于]框架中选中[最大值\最小值]单选按钮。
步骤3 设置可变单元格区域,按Ctrl 键,用鼠标进行选取,或在每选一个连续区域后,在其后输入逗号“,”。
步骤4 单击[约束]框架中的[添加]按钮。
步骤5 在弹出的[添加约束]对话框个输入约束条件.
步骤6 单击[添加]按钮、完成一个约束条件的添加。
重复第5步,直到添加完所有条件
步骤7 单击[确定]按钮,返回到[规划求解参数]对话框,完成条件输入的[规划
求解参数]对话框。
步骤8 点击“求解器参数”窗口右边的“选项”按钮。
确信选择了“采用线性模型”旁边的选择框。
这是最重要的一步工作!如果“假设为线性模型”旁边的选择框没有被选择,那么请选择,并点击“确定”。
如果变量全部非负,而“假定变量非负”旁边的选择框没有被选择,那么请选择,并点击“确定”。
步骤9 单击[求解]按钮,弹出[规划求解结果]对话柜,同时求解结果显示在工作表中。
步骤10 若结果满足要求,单击[确定]按钮,完成操作;若结果不符要求,单击
[取消]按钮,在工作表中修改单元格初值后重新运行规划求解过程。
例 利用Excell 工作表求解线性规划问题
12
121
21212max 1502102310034120..55150
,0z x x x x x x s t x x x x =++≤⎧⎪+≤⎪⎨+≤⎪⎪≥⎩ 。
解:1 将光标方在目标函数值存放单元格(C7),点击“工具”,出现下图:
2 点击“规划求解”出现下图
如果是求最小值问题,选择“最小值”。
3.在可变单元格中选择决策变量单元格B2,C2,出现下图。
4. 点击“添加”,出现下图。
5.输入约束条件
6. 输入约束条件,点击“确定”,出现下图。
7. 点击“选项”,出现下图。
如果“采用线性模型”前没有√,点击“采用线性模型”;如果“假定非负”前
没有√,点击“假定非负”。
8. 点击确定,回到规划求解对话框,出现下图。
9.点击“求解”,出现下图‘
计算机给出求解信息“规划问题找到一解,可满足所有约束条件及最优状况”,这说明,问题有最优解。
10.点击“确定”,回到Excell工作表,出现下图。
在工作表中,给出了最优解情况:
120,30,max 6300x x z === 。
在工具栏中,如果没有“规划求解”项目,可通过“加载宏”添加规划求解功能。
提醒大家注意的是,在计算机安装时,很多计算机的office 软件是典型安装的,这时,需要有office 软件的安装盘。
利用Excell 工作表的规划求解功能,可得案例1.1 火电厂动力配煤问题的最优解为:
1号矿井生产的煤的使用量为0吨;
2号矿井生产的煤的使用量为313.07吨;
2号矿井生产的煤的使用量为649.72吨;
2号矿井生产的煤的使用量为37.2顿:
最小总成本是699193.13元。
下表是相应的Excell 求解表格。